Identification of moving vehicular parameters based on glowworm swarm optimization algorithm

Li, H. L.; Lu, Z. R.; Liu, J. K.

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Identification of moving vehicular parameters based on glowworm swarm optimization algorithm

H. L. Li¹

Z. R. Lu²

J. K. Liu³

^{1, 2, 3}Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou, P. R. China

Corresponding Author:

Z. R. Lu

Cite the article Download PDF

Downloads 1263

Abstract

This paper presents an indirect method for the identification of parameters of moving vehicle based on Glowworm Swarm Optimization (GSO) algorithm. And a local search method is introduced in the movement phase of GSO to enhance the accuracy and convergence rate. The moving vehicle is modeled as 2-DOF systems with five parameters. And Newmark direct integration method is used to calculate the dynamic response of the system. Acceleration measurements at selected stations on the vehicle are used only to identify the parameters of the moving vehicle. Several test cases are carried out to illustrate the efficiency of the method and the results show that the vehicle parameters can be identified precisely with the proposed method and it is not sensitive to measurement noise.

1. Introduction

Vehicular parameters identification is an important problem relevant to many fields, such as, the analysis of dynamic response of vehicle-bridge system [1] and the structural health monitoring [2]. And the parameters of vehicle are usually assumed to be known beforehand even though it is unrealistic. Many different optimization methods and techniques for parameter identification have been proposed in early literature [3, 4]. In recent years, parameter identification basing on swarm intelligence optimization algorithm has been developed. Au et al. [5, 6] described a method based on genetic algorithms for the identification of parameters of moving vehicles with the dynamic responses of the bridge.

GSO is a nature-inspired method of swarm intelligence based algorithm for optimizing multi-modal functions proposed by Krishnanand and Ghose [7] in 2005. It has been introduced and applied to solve the optimization problems in different areas, such as, sensor deployment [8] and cluster analysis [9]. Universal as the GSO is, it still has some drawbacks including slow convergence speed and easily trapped into local optima [10]. Many improved algorithm is proposed to enhance the accuracy and convergence rate of GSO [11-13].

In this study, we aim to introduce the GSO to identify the parameters of moving vehicle. A local search strategy is included in the movement phase of GSO to enhance the accuracy and convergence rate of the algorithm. And the Improved Glowworm Swarm Optimization (IGSO) algorithm is used to identify the parameters of the moving vehicle with acceleration measurements at selected stations on the moving vehicle. Several test cases are carried out to verify the efficiency of the method.

2. Dynamic response of the bridge-vehicle system

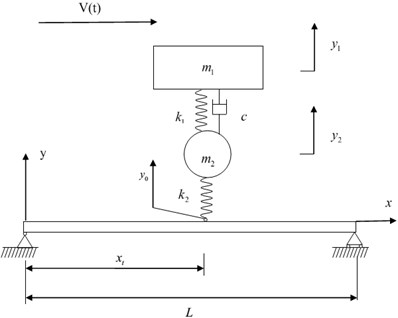
Fig. 1 shows a vehicle-bridge system under study. The bridge is modeled as a linear elastic Bernoulli-Euler beam and the moving vehicle is modeled as 2-DOF systems with five parameters. The equations of motion for the vehicle and the bridge are obtained as follows.

According to the d’Alembert principle, the equation of motion for the vehicle is expressed as:

1

[\begin{matrix} m_{1} & 0 \\ 0 & m_{2} \end{matrix}] [\begin{array}{l} {\ddot{y}}_{1} \\ {\ddot{y}}_{2} \end{array}] + [\begin{matrix} c & - c \\ - c & c \end{matrix}] [\begin{array}{l} {\dot{y}}_{1} \\ {\dot{y}}_{2} \end{array}] + [\begin{matrix} k_{1} & - k_{1} \\ - k_{1} & k_{1} + k_{2} \end{matrix}] [\begin{array}{l} y_{1} \\ y_{2} \end{array}] = [\begin{matrix} 0 \\ k_{2} y (x, t) \end{matrix}],

where $m_{1}$ , $m_{2}$ is the upper mass and lower mass of the vehicle, respectively, $k_{1}$ is the primary spring stiffness and $c$ is the damping coefficient of the primary spring, $k_{2}$ is the contact spring stiffness.

After finite element discretization, the forced vibration equation for the bridge can be written as:

2

[M] \{\ddot{y}\} + [C] \{\dot{y}\} + [K] \{y\} = [B] \{F_{b}\},

where $[M]$ , $[C]$ and $[K]$ are the system mass, damping and stiffness matrices respectively. Rayleigh damping model is adopted, i.e., $[C] = a_{1} [M] + a_{2} [K]$ , where $a_{1}$ and $a_{2}$ are two constants. ${\ddot{y}}$ , ${\dot{y}}$ and ${y}$ are the acceleration, velocity and displacement response vectors of the system, ${F_{b}}$ is a vector of interact forces with matrix $[B]$ mapping these forces to the associated degrees-of-freedom of the system and ${F_{b}} = m_{1} g + m_{2} g + k_{2} (y_{2} (x, t) - y_{0} (x, t))$ .

The dynamic responses of the bridge-vehicle system can be obtained using Newmark method.

Fig. 1The vehicle-bridge system under study

3. Identification of moving vehicular parameters based on GSO

3.1. Basic glowworm swarm optimization algorithm

GSO, which is based on the glowworm finding mate by lighting behavior, is proposed by Krishnanand and Ghose in 2005. In GSO, A swarm composed by agents is called glowworms. And the state of glowworm $i$ at time $t$ can be described by the following set of variables: a position in the $n$ -dimension search space, a luciferin level and a neighbourhood range. GSO algorithm describes how these three variables change over time. And it is divided into three main phases: luciferin update phase, movement phase and local-decision range update phase.

Firstly, all glowworms are randomly distributed in the definition space and the luciferin value of each glowworm is calculated by Eq. (3):

3

l_{i} (t + 1) = (1 - ρ) l_{i} (t) + γ J_{i} (t + 1),

where $l_{i} (t)$ is the luciferin value of glowworm $i$ at time $t$ . $ρ$ is the luciferin decay constant and $0 < ρ < 1$ , $γ$ is the luciferin enhancement constant. $J_{i} (t)$ is the value of objective function at the location of glowworm $i$ at time $t$ .

In the movement phase, every glowworm tries to find its neighbors. The set of neighbors of glowworm $i$ at time $t$ is given by:

4

N_{i} (t) = \{j : ‖x_{j} (t) - x_{i} (t)‖ < r_{d}^{i}; l_{i} (t) < l_{j} (t)\},

where $r_{d}^{i}$ is the local-decision range of glowworm $i$ at time $t$ .

Then, each glowworm will chooses one neighbor by random with probability proportional to the luciferin level of this neighbor. Finally, glowworm moves one step to the chosen neighbor. The movements of glowworms can be stated as:

5

x_{i} (t + 1) = x_{i} (t) + s (\frac{x_{j} (t) - x_{i} (t)}{‖x_{j} (t) - x_{i} (t)‖}),

where $s$ is the step size and $‖‖$ means the Euclidean norm operator.

In the local-decision range update, the local-decision range update by Eq. (6):

6

r_{d}^{i} (t + 1) = m i n \{r_{s}, m a x \{0, r_{d}^{i} (t) + β (n_{t} - |N_{i} (t)|)\}\},

where $r_{s}$ is the vision range, $n_{t}$ is the neighbor threshold, $β$ is the change rate of the neighbor range.

3.2. Improved glowworm swarm optimization algorithm (IGSO)

GSO is a derivative-free and meta-heuristic algorithm and it is found to be universal. But the performance of classical GSO suffers from the problem of premature and low accuracy. Huang and Zhou [20] proposed an improved Variation Step Adaptive Glowworm Swarm Optimization (VSAGSO)) to improve the accuracy and to speed up convergence of the GSO. In the VSAGSO, the step length is updated by Eq. (7). It endows a big initial step and the step decreases dynamically with the increase of the iteration. So the convergence speed in the initial stage is improved and the algorithm can get more precise solution in the end:

7

s = s_{0} e x p (- 30 \times {(\frac{t}{T_{m a x}})}^{p}) + s_{m i n},

where $s_{0}$ is the initial step size and $s_{m i n}$ is the minimum of the step size. $T_{m a x}$ is the max number of iteration and $p$ is a contant.

In the movement phase of GSO, the glowworm moves a step to a neighbor with all dimensions in the space. Even though the local convergence speed of GSO is quite good, it might result in the premature convergence in high dimensions problems. In this paper, a new Improved Glowworm Swarm Optimization Algorithm (IGSO) based on the VSAGSO algorithm is proposed by bringing in the local search of Artificial Bee Colony (ABC) algorithm. In IGSO, the glowworms update their positions using Eq. (8) after Eq. (5) and the new position is accepted if its fitness is better than that of the old one. The exploitation process is more precise and the convergence speed is improved:

8

x_{i} (t + 1) = x_{i} (t) + r \times (x_{j} (t) - x_{i} (t)),

where $r$ is a random number and $r \in [0, 1]$ .

3.3. Identification of moving vehicular parameters

An indirect method for the identification of parameters of moving vehicle is presented based on GSO algorithm. And acceleration measurements on the vehicle body and wheel are used only to identify the parameters. The objective function used to identify the vehicle parameters is defined as:

9

J = \sum_{j = 1}^{m} \sum_{i = 1}^{n} {({\ddot{y}}_{s i m u} (i, j) - {\ddot{y}}_{i d e n} (i, j))}^{2},

where ${\ddot{y}}_{s i m u}$ , ${\ddot{y}}_{i d e n}$ are element simulated acceleration vector and identified acceleration vector. $n$ is the total time points and $m$ is all the measurement stations.

In the present identification problem, the position of every glowworm is a set of possible solutions of moving vehicle. In order not to miss the global optimal set of parameters and converge to wrong solution, all glowworms is randomly distributed in a sufficiently large definition space. Then the position of each glowworm, which is treated as a set of vehicular parameters, is put in Eq. (1) and Eq. (2) to get the dynamic responses of the system. Finally, the values of the objective function of all glowworms are obtained and IGSO is adopted to update the positions of all glowworms until the maximum number of iteration is reached.

In this paper, the identification error is defined as:

10

E r = \frac{|P a r a m e t e r_{i d e n} - p a r a m e t e r_{t r u e}|}{p a r a m e t e r_{t r u e}} \times 100 %,

where $P a r a m e t e r_{i d e n}$ , $p a r a m e t e r_{t r u e}$ are the identified and true values of the vehicle parameters.

4. Numercial simulation

Two vehicles moving on a simply-span simply supported bridge is study in this paper. The parameters of the bridge are: flexural rigidity $E I =$ 1.275×10¹¹ Nm², mass density $ρ =$ 2500 kg/m³ and length $L =$ 30 m. The bridge is divided equably into twenty beam elements to calculate the dynamic response of the bridge-vehicle system. And the speed of the vehicle is set to be 15 m/s. The time step is 0.01 s. The first two modal damping ratios are both assumed to be 0.01. The assumed true values and bounds of the parameters of the one-axle vehicle are listed in Table 1.

The parameters of IGSO are set as below: $T_{m a x} =$ 1000, $N =$ 100, $p =$ 3, $ρ =$ 0.4, $γ =$ 0.6, $β =$ 0.08, $n_{t} =$ 5, $s_{0} =$ 50000, and $s_{m i n} =$ 0.2.

Table 1Assumed true values of the vehicle parameters and their bounds

	Parameters	$m_{1}$ (kg)	$c$ (Ns/m)	$k_{1}$ (N/m)	$m_{2}$ (kg)	$k_{2}$ (N/m)
Vehicle No. 1	Assumed value	35 470	70 000	6 700 000	2500	8 340 000
	Lower bound	0	0	0	0	0
	Upper bound	70 000	140 000	13 000 000	5000	17 000 000
Vehicle No. 2	Assumed value	27 000	86 000	9 120 000	4800	5 000 000
	Lower bound	0	0	0	0	0
	Upper bound	70 000	140 000	13 000 000	5000	10 000 000

4.1. Case study 1: basic strategy

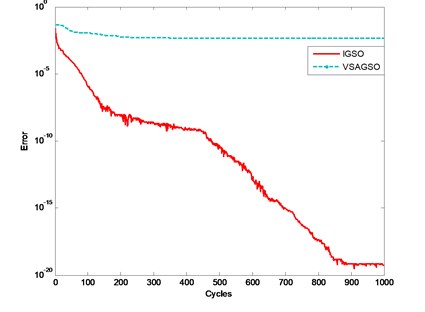
The accuracy and robustness of IGSO and VSAGSO are investigated in this case. The IGSO and VSAGSO are coded in Matlab 2011a and experiments are executed on a inter core i3-3230 CPU PC with 4G RAM. Each benchmark is independently run with every algorithm 20 times for comparisons. The mean value (Mean), standard deviation (Dev), minimum value (Min) and maximum value (Max) in 20 runs are calculated as the statistics for the performances measures. Table 2 shows the results of the best objective function value of IGSO and VSAGSO. It is found that the best objective function value of IGSO is much less than that of VSAGSO. And the robustness of IGSO is very good. Evolution curves of the minimum of the best objective function value are showed in Fig. 2. One can find that the ability of exploitation the solution of IGSO is much better than that of VSAGSO.

Table 2The results of the best objective function values of IGSO and VSAGSO

Method	Mean	Dev	Min	Max
IGSO	2.23×10^-20	2.13×10^-20	0.70×10^-20	8.47×10^-20
VSAGSO	2.82×10^-2	2.38×10^-2	1.61×10^-3	9.16×10^-2

Fig. 2Curves of the best objective function value

4.2. Case study 2: effect of measurement noise

In practice, measurement noise is likely to be contained in the measurement data and the effect of measurement noise on the accuracy and efficiency of the proposed method is investigated in this case. Different noise level in measurement is considered here. It is found that the parameters of the vehicle can be identified with 20 % noise level. And the error of the identified results will be smaller when the noise level decries.

Table 3Summary of the results with different noise level

	Parameters	5 % noise level		10 % noise level		20 % noise level
	Parameters	Identified	Er (%)	Identified	Er (%)	Identified	Er (%)
Vehicle No. 1	$m_{1}$ (kg)	35147	0.91	34824	1.82	34180.41	3.64
	$c$ (Ns/m)	68952	1.50	67913	2.98	65867.84	5.90
	$k_{1}$ (N/m)	6646069	0.80	6591542	1.62	6481753.02	3.26
	$m_{2}$ (kg)	2465	1.42	2429	2.83	2360.30	5.59
	$k_{2}$ (N/m)	8283355	0.68	8226461	1.36	8114312.95	2.71
Vehicle No. 2	$m_{1}$ (kg)	26938	0.23	26875	0.46	26752.83	0.92
	$c$ (Ns/m)	85427	0.67	84810	1.38	83425.38	2.99
	$k_{1}$ (N/m)	9144894	0.27	9170128	0.55	9227574.00	1.18
	$m_{2}$ (kg)	4778	0.46	4756	0.92	4714.66	1.78
	$k_{2}$ (N/m)	4980513	0.39	4960895	0.78	4921579.62	1.57

5. Conclusions

This paper presents an improved method with GSO by bringing a local search strategy to accelerate the convergence speed and improve search precision at the same time. And it is successfully used in the vehicle parameter identification. The responses of the moving vehicle are used only to identify the vehicle parameters. The numerical example shows that IGSO has better robustness and search precision. The vehicle parameters can be identified precisely with IGSO and it is not sensitive to the measurement noise.

References

Wang W. J., Lu Z. R., Liu J. K. Time-frequency analysis of a coupled bridge-vehicle system with breathing cracks. Interaction and Multiscale Mechanics, Vol. 5, Issue 3, 2012, p. 169-185.

Search CrossRef
Zhu X. Q., Law S. S. Damage detection in simply supported concrete bridge structure under moving vehicular loads. Journal of Vibration and Acoustics, Vol. 129, Issue 1, 2007, p. 58-65.

Search CrossRef
Michelberger P., Bokor J., Keresztes A., et al. Identification of a multivariable linear model for road vehicle (bus) dynamics from test data. International Journal of Vehicle Design, Vol. 8, Issue 1, 1987, p. 96-114.

Search CrossRef
Goheen K. R., Jefferys E. R. The application of alternative modelling techniques to ROV dynamics. IEEE International Conference on Robotics and Automation, 1990, p. 1302-1309.

Search CrossRef
Au F. T. K., Jiang R. J., Cheung Y. K. Parameter identification of vehicles moving on continuous bridges. Journal of Sound and Vibration, Vol. 269, Issue 1, 2004, p. 91-111.

Search CrossRef
Jiang R. J., Au F. T. K., Cheung Y. K. Identification of vehicles moving on continuous bridges with rough surface. Journal of Sound and Vibration, Vol. 274, Issue 3, 2004, p. 1045-1063.

Search CrossRef
Krishnanand K. N. D., Ghose D. Glowworm swarm optimization: a new method for optimizing multi-modal functions. Computational Intelligence Studies, Vol. 1, Issue 1, 2009, p. 93-119.

Search CrossRef
Liao W. H., Kao Y., Li Y. S. A sensor deployment approach using glowworm swarm optimization algorithm in wireless sensor networks. Expert Systems with Applications, Vol. 38, Issue 10, 2011, p. 12180-12188.

Search CrossRef
Huang Z. X., Zhou Y. Q. Using glowworm swarm optimization algorithm for clustering analysis. Journal of Convergence Information Technology, Vol. 6, Issue 2, 2011, p. 78-85.

Search CrossRef
Zhou Y., Liu J., Zhao G. Leader glowworm swarm optimization algorithm for solving nonlinear equations systems. Przeglad Elektrotchniczny, Vol. 1b, 2012, p. 101-106.

Search CrossRef
He D., Zhu H. Glowworm swarm optimization algorithm based on multi-population. Sixth International Conference on Natural Computation, Vol. 5, 2010, p. 2624-2627.

Search CrossRef
Wu B., Qian C., Ni W., et al. The improvement of glowworm swarm optimization for continuous optimization problems. Expert systems with applications, Vol. 39, Issue 7, 2012, p. 6335-6342.

Search CrossRef
Huang K., Zhou Y. Q. Improved variation step adaptive GSO algorithm. Computer Engineering, Vol. 38, Issue 4, 2012, p. 185-187.

Search CrossRef

About this article

Received

Accepted

02 August 2015

Published

18 September 2015

SUBJECTS

Vibration in transportation engineering

Keywords

glowworm swarm optimization algorithm

bridge-vehicle system

dynamic response

moving vehicle

parameter identification

Acknowledgements

The work described in this paper is supported by the National Natural Science Foundation of China (11172333, 11272361), Doctoral Program Foundation of Ministry of Education of China (20130171110039), and the Guangdong Province Science and Technology Program (2012A030200011, 2014A020218004). Such financial aids are gratefully acknowledged.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.