Rolling element bearings fault diagnosis based on CEEMD and SVM

1. Introduction

By reducing costs and decreasing the repair time, condition based maintenance becomes an efficient strategy for modern industry [1]. Rolling element bearings are one of the essential components in most of the machinery [2]. It directly influences the operation of the whole machinery. The majority of the problems in rotating machines are caused by faulty bearings. Faults which typically occur in rolling element bearings are usually caused by localized defects in the outer-race, the inner-race, or the rollers. Such defects generate a series of impact vibrations every time a running roller passes over the surfaces of the defects. Therefore, it is significant to be able to accurately and automatically detect and diagnose the existence and severity of the faults occurring in the bearings. Since vibration signals carry a great deal of information representing mechanical equipment health conditions, the vibration based signal processing technique is one of the principal tools for diagnosing bearing faults [3, 4].

Typically, a fault diagnosis system containing two steps, the first step is to extract fault features by signal processing; the second step is to diagnose the faults by the characteristic information obtained in the first step. With the signal processing techniques, faulty characteristic information can be extracted from the vibration signals [5]. Considering the nonstationary of the rolling element bearing vibration signal, the time frequency analysis methods such as wavelet transform (WT) [6, 7] and Empirical Mode Decomposition (EMD) [8] were used for processing the complex signal. EMD method introduced by Huang et al. is an innovative time-series analysis tool in comparison with traditional methods such as Fourier methods, wavelet methods, and empirical orthogonal functions. A nonstationary and nonlinear signal will be decomposed into several IMF components by the sifting process of EMD. The result is a set of very nearly orthogonal functions and the number of functions in the set depends on the original signal [9, 10]. One of the primary weaknesses of EMD method is the phenomenon of mode mixing, which is defined as either a single intrinsic mode function (IMF) containing signals of widely different scales, or a signal of a similar scale existing in different IMF components. In order to overcome the shortcomings of EMD, A noise-assisted data analysis method called ensemble EMD (EEMD) was proposed by Wu and Huang [11] to restrain the mode mixing problem of EMD by adding white noise to the initial data. The resulting IMFs derived from EEMD, however, would inevitably be polluted by the added noise especially when the number of trials was in appropriate and this can be really true when reconstructing the original signal from the obtained IMFs. Recently, an enhanced EEMD algorithm called complementary EEMD (CEEMD) was proposed to improve the efficiency of the original noise assisted method by adding noise in pairs with plus and minus signs [12]. Compared with EEMD, the greatest advantage of CEEMD is an exact cancellation of the residual noise in reconstruction of the original signal when the results derived by CEEMD are the same as EEMD.

In recent years, SVM has been widely used in many research areas, such as face recognition, signal and image processing and fault diagnosis. SVM based classifiers have better generalization properties than ANN based classifiers. The efficiency of SVM based classifier does not depend on the number of features. This property is very useful in fault diagnostics because the number of features to be chosen is not limited, which make it possible to compute directly using original data without pre-processing them to extract their features. These advantages make SVM an excellent choice for the fault detection and localization applications [13]. Meanwhile SVM kernel function parameters selection problem is an important factor affecting the performance of classification ability, Genetic Algorithm (GA) was used for optimizing the kernel function parameters selection.

In this paper, CEEMD was used to extract fault features of rolling element bearings. In order to eliminate redundancy feature information, Principal Component Analysis (PCA) was used to reduce the dimension of the feature vectors. SVM kernel function parameters were optimized by GA. At last, SVM was selected for rolling element bearings fault condition identifying and its diagnosis ability was compared with BP neural networks.

2. CEEMD and SVM method

3. Rolling element bearings fault diagnosis method

Rolling element bearings fault diagnosis method based on CEEMD and SVM is showed as follows:

(1) Decomposing the original signal into several IMF components by CEEMD, and then selecting the IMF components containing the main fault information;

(2) Calculating the characteristics factor of the IMF components, total energy $E_j$, kurtosis $K_j$, form factor $X_{sf}$, peak factor $X_{cf}$:

(3) Constructing the feature vector $P$ by the total energy $E_j$, kurtosis $K_j$, form factor $X_{sf}$, peak factor $X_{cf}$, $P=\left[E_j,K_j,X_{sf},X_{cf}\right]$.

(4) Normalizing the feature vectors in order to reduce the interference to SVM caused by the large differences in data.

(5) Using principal component analysis (PCA) method for feature vector dimensions reduction, eliminating data redundancy and shortening the calculation time.

(6) The RBF kernel functions and one-to-one multi-classification method are selected for SVM classification. Because in most cases, they proved to be better than other kernel functions and multi-classification structures.

(7) GA-optimized kernel functions parameters and penalty factor are used for SVM training.

4. Applications

The ball Bearings test data for normal and faulty Bearings is provided by Case Western Reserve University Bearings Data Center [16]. Experiments are conducted using a 2 hp Reliance Electric motor, and acceleration data is measured at locations near to and remote from the motor Bearings.

As shown in Fig. 1, the test stand consists of a 2 hp motor (left), a torque transducer/encoder (center), a dynamometer (right), and control electronics (not shown). The test bearings support the motor shaft. Motor Bearings are seeded with faults using electro-discharge machining (EDM). Faults ranging from 0.007 inches in diameter to 0.040 inches in diameter are introduced separately at the inner raceway, rolling element (i.e. ball) and outer raceway. Faulted Bearings are reinstalled into the test motor and vibration data is recorded for motor loads of 0 to 3 horsepower (motor speeds of 1797 to 1720 RPM). Vibration data is collected using accelerometers, which are attached to the housing with magnetic bases. Accelerometers are placed at the 12 o’clock position at both the drive end and fan end of the motor housing. During some experiments, an accelerometer is attached to the motor supporting base plate as well. In this application, the two typical conditions 1730 RPM and 1772 RPM are selected for the proposed method verification.

Fig. 1Schematic diagram of the Bearings testing setup

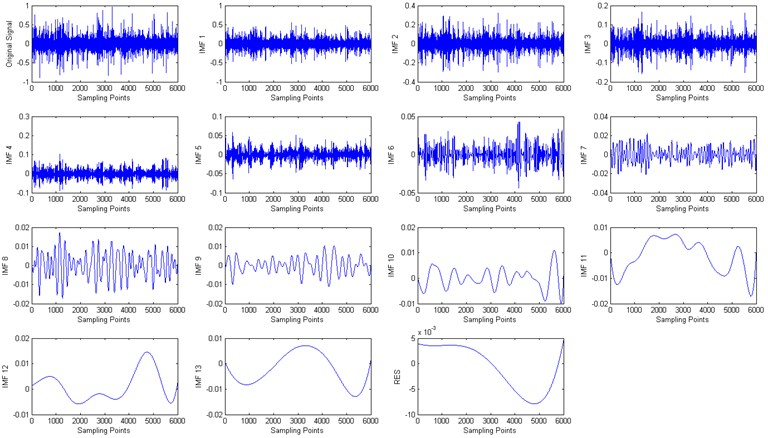
The vibration signal is decomposed into 13 IMF components and a residual component (RES) by CEEMD. In Fig. 2, the first figure is the original signal, the remaining are 13 IMF components and a residual component. Limitations of space prevent us from covering all the fault conditions, only give the CEEMD decomposition result of ball defects condition in 1772 RPM. The IMF components containing the key information are selected and then arrange them from low frequency to high frequency, $c_1\left(t\right)$, $c_2\left(t\right)$,…, $c_5\left(t\right)$. After that the fault feature vectors are calculated by foregoing Eq. (5).

In this experiment, there are four fault conditions consisting of Normal Bearings running condition, Inner-race defect, rolling element defect, and Outer-race defect. And 40 samples are selected for training, including 10 normal running samples, 30 samples of failures, and 40 samples for testing (10 in each case). A 20 dimensions feature vector is constructed by the total energy $E_j$, kurtosis $K_j$, form factor $X_{sf}$ and peak factor $X_{cf}$ in the five IMF components. In order to eliminate data redundancy and reduce computing time, PCA is used for feature vectors dimension reduction. After that, the feature vector of condition 1 (1730 RPM) and condition 2 (1772 RPM) are reduced to five-dimensional feature vectors.

When establishing SVM classification models, kernel function and its parameters puzzle SVM users. Radial Basis Function is selected as kernel function due to it has better generalization ability. GA is used for optimizing kernel functions parameters and penalty factor selecting. In the BP neural networks, input layer neuron number $m$ is 5, output layer neuron number $n$ is 4, the hidden layer neuron number is determined by the empirical formula $l=\sqrt{m+n}+\alpha$ and $\alpha$ is generally between (1, 10). So the hidden layer neuron number is set as 8. Then the feature vectors are employed for classification models training.

Fig. 2The CEEMD decomposition results of vibration signal of rolling element bearings with rolling element defect in condition 2 (1772 RPM)

5. Results and discussion

SVM and BP neural networks are adopted for rolling element bearings fault classification in the two conditions respectively, and the results are shown in Table 1.

The classification results of SVM and BP neural networks in the two working conditions were showed in the Table 1, including diagnosis accuracy and time. The diagnostic results reach a high accuracy with all of it are higher than 94 %, at the same time, the computing speed is fast with the diagnostic time is less than 2 seconds. Then, the experimental results between SVM and BP neural networks are compared. We can found that the GA-optimized SVM performance better than BP neural networks on not only diagnostic accuracy but also diagnostic time.

The CEEMD method is an adaptive method to analyze instability and nonlinearity that can decompose the vibration signal into several IMF components. The characteristic frequencies of different bearing faults are in different IMF components or different faults conduce to variable feature such as energy or kurtosis in IMF components. PCA method could reduce feature vector dimensions and decrease diagnostic time. The GA-optimized SVM clearly perform better than BP neural networks, which is widely recognized by scholars.

However, in the real world rolling element bearing fault diagnosis, CEEMD is a noise aided method that the CEEMD decomposition results may be disturbed by the noise in the vibration signal. At the same time, the noise affects the CEEMD parameter selection. This might to be a problem when the method used in the real world. Further investigation should be done to decrease the influence of the noise, maybe the denoising method is a solution.

6. Conclusions

In this paper, a novel method for fault diagnosis of rolling element bearings based on CEEMD and SVM is presented. In order to detect the bearing fault occurrence, the improved EMD is employed for decomposing the vibration signal into IMF components, through Fast Fourier transform of the IMF components we can find the faulty characteristic frequency of rolling element bearings. The energy, kurtosis, form factor and peak factor of the IMF components containing main fault characteristic are calculated for constructing the feature vector, and PCA was adopted for feature vector dimensions reduction. Finally, GA-optimized SVM method and BP neural networks are used for fault recognition. The application analysis results indicate that fault feature extracted by CEEMD is effective; PCA can reduce the computational complexity of the data; compared with BP neural networks, SVM not only has better diagnosis accuracy, but also saves the processing time for rolling element bearings diagnosis.