Vibration signal simulation of planetary gearbox based on motion process modeling

Zhao, Jianmin; Li, Haiping; Liu, Jian; Kong, Fansheng

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Vibration signal simulation of planetary gearbox based on motion process modeling

Jianmin Zhao¹

Haiping Li²

Jian Liu³

Fansheng Kong⁴

^{1, 2}Mechanical Engineering College, Shijiazhuang, 050003, China

³College of Communication and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing, 210003, China

⁴The Army of 63853, Baicheng, 137001, China

Corresponding Author:

Haiping Li

Cite the article Download PDF

Downloads 1195

Abstract

In planetary gearbox, multiple gear pair meshing with each other and the vibration transmission paths from gear meshing points to the fixed sensors are time-varying. Therefore, fault diagnosis of the planetary gearbox is more difficult compared to that of fixed-axis gearbox, in which the vibration signal simulation models are very important. This paper constructs vibration signal models based on motion process modeling. This kind of modeling method is easier to understand compare with other methods which mainly based on the theory or physical laws behind the phenomena. The modeling process was presented in a step-by-step procedure according to the motion process of planetary gearbox. Frequency analysis was also implemented and comprehensive diagram was shown to help understand the result.

1. Introduction

Compared with ﬁxed shaft gearboxes, planetary gears can provide a larger transmission ratio in a more compact package. However, a failure of gearbox may cause shutdown of the entire train and result in major economic losses. Therefore, the fault diagnosis of the planetary gearbox is crucial to prevent the mechanical system from malfunction.

Many techniques have been used in planetary gearbox fault diagnosis. Such as support vector machine (SVM) [1], wavelet packet transformation (WPT) [2], empirical mode decomposition (EMD) [3] and hidden Markov model (HMM) [4]. Anyway, in order to diagnose the failure of planetary gearbox more accurately, analyzing its operation mechanism and developing vibration signal simulation models is very important. August and Kasuba [5] studied the elastic mechanics theory of planetary gearbox in late 1980s. Kuang and Lin [6] developed the models of failure with considering the effect of meshing rigidity, damping and friction. However, the equations are too complex to understand. Choy [7] constructed a model of several kinds of fault types, but the final result is unsatisfactory.

This paper constructs vibration signal models based on motion process modeling. This kind of modeling method is easier to understand compare with other methods which mainly based on the theory or physical laws behind the phenomena.

The remaining sections of this paper are organized as follows. In Section 2, the vibration signal simulation model is developed, frequency analysis is implemented and comprehensive diagram is shown. The conclusions were drawn in Section 3.

2. Vibration signal simulation models

2.1. Only considering the planet-ring gear meshing process

The common planetary gearbox consists of sun gear, planet gears, ring gear, carrier etc., as Fig. 1 shows. This paper chooses the structure as an example to conduct vibration signal models. Firstly, two assumptions should be considered before modeling:

(1) The vibration signal only generated in planet-ring gear meshing process;

(2) Ignore the influence of different transmission paths; vibration signal is transmitted from meshing point to the sensor directly through the ring gear after generating, and the sensor is set up on the box which fixed with the ring gear.

Fig. 1Planetary gearbox and measurement arrangement

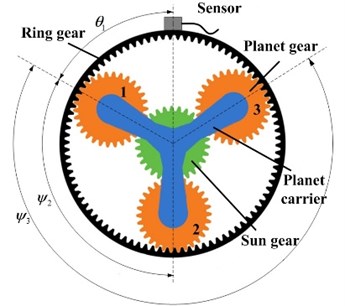
Then, the modeling process will be easy. Assume the vibration signal acquired by the sensor $v_{i}^{r} (t)$ , $i = 1,2, . . ., N$ is generated by $N$ planet gears meshing with ring gear. Due to the special structure, the relative phases between the vibration signals are different. The phase difference $γ_{r i}$ between vibration signals generated in the $i$ th planet-ring meshing process $v_{i}^{r} (t)$ and the vibration signal generated in the first planet-ring meshing process $v_{1}^{r} (t)$ can be calculated as follows:

1

γ_{r i} = ψ_{i} Z_{R} / 2 π,

where $ψ_{i}$ is the relative angle between the position of the ith planet gear and the first planet ( $ψ_{1} = 0$ ), as Fig. 1 shows. $Z_{R}$ is the teeth number of the ring gear.

So, there is a shifted equation between $v_{i}^{r} (t)$ and $v_{1}^{r} (t)$ as follows:

2

v_{i}^{r} (t) = v_{1}^{r} (t - γ_{r i} T_{m}),

where $T_{m} = 1 / f_{m}$ is the mesh period of the planetary gearbox.

As the gears rotates, the meshing points between planet gears and the ring gear moves. So, the distance between the source of vibration signal and the sensor varies. This will make the amplitude of the vibration signal varies. The process is called amplitude modulation. Since the planet gears are mounted on the planet carrier, the amplitude modulation effect repeats once per revolution of the planet carrier. Thus, the amplitude modulation function $a_{i}^{r} (t)$ is periodic with a fundamental frequency $f_{C}$ . Similar to $v_{i}^{r} (t)$ and $v_{1}^{r} (t)$ , there is a shifted equation between $a_{i}^{r} (t)$ and $a_{1}^{r} (t)$ as follows:

3

a_{i}^{r} (t) = a_{1}^{r} (t - \frac{ψ_{i} T_{C}}{2 π}),

where $T_{C} = 1 / f_{C}$ is the rotate period of the planet carrier.

Thus, the amplitude-modulated vibration signals generated in the meshing process of the $i$ th planet and ring gear can be expressed as follows:

4

x_{i}^{r} (t) = a_{i}^{r} (t) v_{i}^{r} (t) .

The vibration signal generated in the meshing process of all planet gears with the ring gear occurs at the same time, so the sum of all signal acquired by the sensor can be expressed as:

5

x^{r} (t) = \sum_{i = 1}^{N} x_{i}^{r} (t) = \sum_{i = 1}^{N} a_{i}^{r} (t) v_{i}^{r} (t) = \sum_{i = 1}^{N} a_{1}^{r} (t - \frac{ψ_{i} T_{C}}{2 π}) v_{1}^{r} (t - γ_{r i} T_{m}) .

Additionally, duo to the position of the first planet gear is uncertain, i.e. $θ_{1}$ is uncertain, a new parameter $t_{1} = θ_{1} / 2 π f_{C}$ will be introduced to Eq. (5). Therefore, the vibration signal generated in the planet-ring gear meshing process can be expressed as:

6

x^{r} (t) = \sum_{i = 1}^{N} x_{i}^{r} (t) = \sum_{i = 1}^{N} a_{i}^{r} (t) v_{i}^{r} (t) = \sum_{i = 1}^{N} a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π}) v_{1}^{r} (t - γ_{r i} T_{m}) .

Eq. (6) describes the vibration signal generated by planet-ring meshing process and acquire by a sensor mounted on the box.

2.2. Theoretical frequency analysis

As described above, the vibration signal model has been obtained. In order to analyze the health condition of the planetary gearbox, theoretical frequency analysis should be implemented. Fourier transform (FT) is the main tool of frequency analysis. Assume the system is linear, and then the FT of Eq. (6) is:

7

X^{r} (f) = \sum_{i = 1}^{N} X_{i}^{r} (f) = \sum_{i = 1}^{N} \underset{I}{\underset{⏟}{F \{a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π})\}}} * \underset{I I}{\underset{⏟}{F \{v_{1}^{r} (t - γ_{r i} T_{m})\}}},

where $F \{\cdot\}$ represents the FT, $*$ represents the convolution. It can be seen that $X^{r} (f)$ is the sum of the convolution of $N$ (I) and (II). And the (I) is considered at first. Due to $a_{i}^{r} (t)$ is periodic with a fundamental frequency $f_{C}$ , it can be decomposed by FT as follows:

8

a_{i}^{r} (t) = a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π}) = \sum_{q \in Z} α_{q}^{r} e^{j 2 π q f_{C} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π})},

where $α_{q}^{r}$ , $q \in Z$ is the Fourier coefficients of $a_{1}^{r} (t)$ . Additionally, according to the Eq. (3), the FT of (I) can be calculated as follows:

9

F \{a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π})\} = \sum_{q \in Z} α_{q}^{r} e^{- j 2 π q f_{C} (t_{1} + \frac{ψ_{i} T_{C}}{2 π})} δ (f - q f_{C}),

where the Function $δ$ has the property that:

10

\{\begin{array}{l} δ (x) = 1, & x = 0, \\ δ (x) = 0, & x \neq 0 . \end{array}

Then the (II) is considered. Similarly, $v_{i}^{r} (t)$ can be decomposed by FT as follows:

11

v_{i}^{r} (t) = v_{1}^{r} (t - γ_{r i} T_{m}) = \sum_{k \in Z} β_{k}^{r} e^{j 2 π k f_{m} (t - γ_{r i} T_{m})},

where $β_{k}^{r}$ , $k \in Z$ is the Fourier coefficients of $v_{1}^{r} (t)$ . And the FT of (II) can be calculated as follows:

12

F \{v_{1}^{r} (t - γ_{r i} T_{m})\} = \sum_{k \in Z} β_{k}^{r} e^{- j 2 π k f_{m} γ_{r i} T_{m}} δ (f - k f_{m}) .

Substituting the Eq. (1), (9) and (12) into Eq. (7):

13

X^{r} (f) = \sum_{i = 1}^{N} X_{i}^{r} (f) = \sum_{i = 1}^{N} F \{a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π})\} * F \{v_{1}^{r} (t - γ_{r i} T_{m})\}

= \sum_{k \in Z} \sum_{q \in Z} \sum_{i = 1}^{N} α_{q}^{r} β_{k}^{r} e^{- j 2 π q f_{C} (t_{1} + \frac{ψ_{i} T_{C}}{2 π})} e^{- j 2 π k f_{m} γ_{r i} T_{m}} δ (f - k f_{m} - q f_{C})

= \sum_{k \in Z} \sum_{q \in Z} \sum_{i = 1}^{N} α_{q}^{r} β_{k}^{r} e^{- j 2 π q f_{C} t_{1}} e^{- j (k Z_{R} + q) ψ_{i}} δ (f - k f_{m} - q f_{C}) .

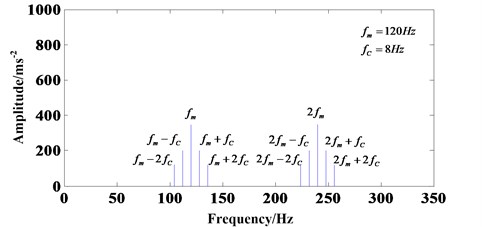
The $δ (f - k f_{m} - q f_{C})$ implies that $X^{r} (f) \neq 0$ only when $f = k f_{m} + q f_{C}$ and $k, q \in Z$ . Namely, only considering the planet-ring gear meshing process, $q f_{C}$ will be existent as sidebands around $k f_{m}$ . Fig. 2 shows this phenomenon very well.

Fig. 2Frequency spectrum diagram with only considering planet-ring gear meshing process

2.3. Effect of the sun-planet gear meshing process

The vibration signal $v_{i}^{s} (t) i = 1,2, . . ., N$ generated in the sun-planet gear meshing process is considered in this section. Similarly, two assumptions are made before modeling:

(1) The vibration signal generated in planet-ring gear and sun-planet gear meshing;

(2) Ignore the influence of different transmission paths; vibration signal is transmitted from meshing point to the sensor directly through the ring gear after generating, and the sensor is set up on the box which fixed with the ring gear.

According to the different transmission distances, two amplitude modulation functions $a_{i}^{r} (t)$ and $a_{i}^{s} (t)$ are used for vibration signal $v_{i}^{r} (t)$ and $v_{i}^{s} (t)$ , respectively. And they are both periodic with a fundamental period $T_{C} = 1 / f_{C}$ . However, due to the signal transmission distance of sun-planet ring meshing process is longer than the signal transmission distance of planet-ring gear meshing process, so $|a_{i}^{s} (t)| < |a_{i}^{r} (t)|$ .

It is also need to be considered that the relative phases between all vibration signal $v_{i}^{s} (t)$ . Similar to $v_{i}^{r} (t)$ , the phase difference $γ_{s i}$ between vibration signals generated in the $i$ th sun-planet meshing process $v_{i}^{s} (t)$ and the vibration signal generated in the first sun-planet meshing process $v_{1}^{s} (t)$ can be calculated as follows:

14

γ_{s i} = ψ_{i} Z_{S} / 2 π,

where $Z_{S}$ is the teeth number of the sun gear.

It can be demonstrated that $γ_{s i} = γ_{r i}$ [8]. In addition, due to a planet gear meshes with sun gear and ring gear at the same time but the distances to the sensor of the vibration signal generated in the two meshing processes are different, so there is a phase difference $γ_{s r}$ between $v_{i}^{s} (t)$ and $v_{i}^{r} (t)$ . Thus, there is a shifted equation between $v_{i}^{s} (t)$ and $v_{1}^{s} (t)$ as follows:

15

v_{i}^{s} (t) = v_{1}^{s} (t - (γ_{r i} + γ_{s r}) T_{m}) .

And there is a shifted equation between $a_{i}^{s} (t)$ and $a_{1}^{s} (t)$ :

16

a_{i}^{s} (t) = a_{1}^{s} (t - \frac{ψ_{i} T_{C}}{2 π}) .

Duo to the position of the first planet gear is uncertain; the vibration signal generated in the sun-planet gear meshing process can be expressed as:

17

x^{s} (t) = \sum_{i = 1}^{N} x_{i}^{s} (t) = \sum_{i = 1}^{N} a_{i}^{s} (t) v_{i}^{s} (t) = \sum_{i = 1}^{N} a_{1}^{s} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π}) v_{1}^{s} (t - (γ_{r i} + γ_{s r}) T_{m}) .

Therefore, considering both planet-ring bot sun-planet gear meshing process, the synthetical vibration signal $x^{r, s} (t)$ can be expressed as:

18

x^{r, s} (t) = x^{r} (t) + x^{s} (t) = \sum_{i = 1}^{N} x_{i}^{r} (t) + \sum_{i = 1}^{N} x_{i}^{s} (t) = \sum_{i = 1}^{N} a_{i}^{r} (t) v_{i}^{r} (t) + \sum_{i = 1}^{N} a_{i}^{s} (t) v_{i}^{s} (t)

= \sum_{i = 1}^{N} a_{1}^{r} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π}) v_{1}^{r} (t - γ_{r i} T_{m})

+ \sum_{i = 1}^{N} a_{1}^{s} (t - t_{1} - \frac{ψ_{i} T_{C}}{2 π}) v_{1}^{s} (t - (γ_{r i} + γ_{s r}) T_{m}) .

For the purpose of frequency analysis, FT of Eq. (18) is calculated as follows:

19

X^{r, s} (f) = X^{r} (f) + X^{s} (f) = \sum_{i = 1}^{N} X_{i}^{r} (f) + \sum_{i = 1}^{N} X_{i}^{s} (f)

= \sum_{k \in Z} \sum_{q \in Z} \sum_{i = 1}^{N} [α_{q}^{r} β_{k}^{r} + α_{q}^{s} β_{k}^{s} e^{- j 2 π k γ_{s r}}] e^{- j 2 π q f_{C} t_{1}} e^{- j (k Z_{R} + q) ψ_{i}} δ (f - k f_{m} - q f_{C}),

where $α_{q}^{s}$ , $β_{k}^{s}$ are the Fourier coefficients of $a_{1}^{s} (t)$ and $v_{1}^{s} (t)$ , respectively.

Fig. 3Frequency spectrum diagram with considering planet-ring and planet-sun gear meshing process

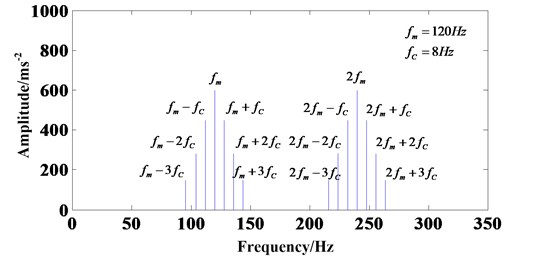
The $δ (f - k f_{m} - q f_{C})$ implies that $X^{r} (f) \neq 0$ only when $f = k f_{m} + q f_{C}$ and $k, q \in Z$ . Fig. 3 can explain the result loudly. Without considering the transfer path effect, only considering the sun-planet and planet-ring gear meshing process, $q f_{C}$ will be existent as sidebands around $k f_{m}$ . However, the amplitude of the signal will be higher than before through the contrast of Eq. (13) and (19).

3. Conclusions

Vibration signal simulation model for planetary gearbox was developed based on motion process modeling. The model considered both planet-ring and sun-planet gears meshing processes. The modeling process was presented in a step-by-step procedure according to the motion process of planetary gearbox. Then, frequency analysis was also implemented and comprehensive diagram was shown to help understand the result.

The shortage of this paper is the vibration signal models of fault gears are not constructed and the effect of transmission path is not considered. These will be the research contents that need to be studied more thoroughly.

References

Baccarini L. M. R., Silva V. V. R., et al. SVM practical industrial application for mechanical faults diagnostic. Expert Systems with Applications, Vol. 38, Issue 6, 2011, p. 6980-6984.

Search CrossRef
Fan X. F., Zuo M. J. Gearbox fault detection using Hilbert and wavelet packet transform. Mechanical Systems and Signal Processing, Vol. 20, Issue 4, 2006, p. 966-982.

Search CrossRef
Ricci R., Pennacchi P. Diagnostics of gear faults based on EMD and automatic selection of intrinsic mode functions. Mechanical Systems and Signal Processing, Vol. 25, Issue 3, 2011, p. 821-838.

Search CrossRef
Kang J. S., Zhang X. H. Application of hidden Markov models in machine fault diagnosis. Information – an International Interdispilinary Journal, Vol. 15, Issue 12B, 2012, p. 5829-5838.

Search CrossRef
August A., Kasuba R. Torsional vibration and dynamic loads in a basic planetary gear system. Journal of Acoustics, Stress, and Reliability in Design, Transaction of the ASME, Vol. 108, 1986, p. 348-353.

Search CrossRef
Kuang J. H., Lin A. D. The effect of tooth wears on the vibration spectrum of a spur gear pair. Journal of Vibration and Acoustics, Vol. 123, 2001, p. 311-317.

Search CrossRef
Choy F. K., Polysckchuk V., Zakrajsek J. J., et al. Analysis of the effects of surface pitting and wear on the vibration of a gear transmission system. Tribology International, Vol. 29, Issue 1, 1996, p. 77-83.

Search CrossRef
Parker R. G., Lin J. Mesh phasing relationship in planetary and epicyclical gears. Journal of Mechanical Design, Vol. 124, 2004, p. 365-370.

Search CrossRef

About this article

Received

Accepted

09 September 2015

Published

18 September 2015

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

planetary gearbox

signal simulation

motion process modeling

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.