Finite element analysis of coupled vibration for hoisting cable with time-varying length

Wang, Jinjie; Cao, Guohua; Lin, Mingxing; Liu, Shanzeng

Vibroengineering Procedia

Browse Procedia

Published: 09 October 2015

Check for updates

Finite element analysis of coupled vibration for hoisting cable with time-varying length

Jinjie Wang¹

Guohua Cao²

Mingxing Lin³

Shanzeng Liu⁴

^{1, 2}Jiangsu Key Laboratory of Mine Mechanical and Electrical, Xuzhou, China

^{1, 2, 4}School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou, China

³School of Mechanical Engineering, Shandong University, Jinan, China

Corresponding Author:

Guohua Cao

Cite the article Download PDF

Downloads 1439

Abstract

The coupled axial-torsional responses of the hoisting cable with time-varying length are investigated in order to predict the longitudinal vibration more accurately. The equations of motion are formulated by Hamilton’s principle and the finite element method (FEM), in which a variable-length cable element is introduced. In order to validate this theoretical model, an ADAMS simulation model is established in the framework of the multi-body system dynamic. The result shows that the numerical solution is in reasonably good agreement with the ADAMS simulation. The frequencies of the cables with the coupling considered and neglected are analyzed by varying the excitation frequency, which indicates that the coupling effect reduces the natural frequency of the cable and the maximum amplitude shifts from the resonance region to the deceleration stage as the coupling coefficient increases.

1. Introduction

Cables, due to their light weight and their ability to resist relatively large axial loads, have been extensively employed in diverse engineering applications [1-3]. However, they are subjected to large-amplitude vibrations for their high flexibility and low internal damping. Thus, the dynamic behavior of cables has been studied widely for decades. Recently, the coupled vibration of the cable with time-varying length has attracted a great deal of attention and various approaches have been proposed. Wang et al. [4] analyzed the coupled lateral- transverse-longitudinal dynamics of an underwater, drawn cable with an attached mass. A variable-domain element is adopted to discretize the equations of motion. Later, Kaczmarczyk and Ostachowicz [5] exhibited the coupled lateral-longitudinal dynamic response of the catenary-vertical ropes in the deep mine hoisting system and obtained the numerical solution by using the Rayleigh-Ritz method. Zhang et al. [6] presented the coupled lateral-longitudinal vibration model of the vertically translating elevator cables subjected to the general initial conditions and the external excitation with Galerkin method.

Cables are characterized by the coupled axial-torsional behavior when subjected to the external loads. Therefore, the vibration analysis of the coupled axial-torsional cable is of great significance. Samras [7] tested experimentally the coupling coefficients and discovered that the axial-torsional stiffness coefficient is approximately equal to the torsional-axial stiffness coefficient. Hashemi and Roach [8] presented the derivation of a dynamic finite element for the coupled extension-torsion vibration analysis of the cable and evaluated the coupled frequencies.

However, few researchers concentrated on the coupled axial-torsional dynamic responses, caused by the external displacement excitation, of the hoisting cable with time-varying length. Some problems have arisen in the hoisting cable of the mine rescue capsule shown in Fig. 1(a). On one hand, the torsion of hoisting cable is easy to destroy the electric cables wound around the surface of the hoisting cable; on the other hand, the torsion of cable aggravates the longitudinal vibration of itself and brings about the slight rotation of the capsule. These two facts reduce the performance of rescue capsules greatly both on safety and comfort. Therefore, it is significant to recognize the essential difference between the cables with the coupling considered and neglected.

This paper is organized as follows. In Section 2, the finite element model is established by adopting a variable-length element. For purpose of verifying the theoretical model, Section 3 presents the virtual prototype of the hoisting system established by using the ADAMS software package. In Section 4, t the results of the axial and torsional responses from both simulations are compared and the frequencies of the cables with the coupling included and neglected are analyzed. Finally, Section 5 draws some conclusions.

Fig. 1Hoisting system with time-varying length

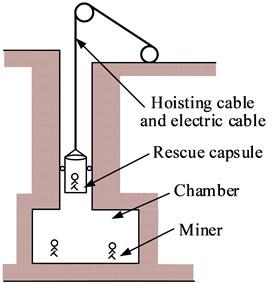
a) Mine rescue capsule

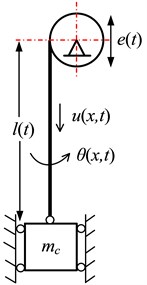
b) Schematic diagram

2. Theoretical investigation

For simplicity, the hoisting system can be modelled as one vertically translating model described by a cylindrical coordinate system. As illustrated in Fig. 1(b), the hoisting cable of length $l (t)$ at time instant $t$ is wound on a head sheave at the top end and is attached with a mass $m_{c}$ at the lower end. The harmonic excitation $e (t) = A s i n (ω t)$ at position $x =$ 0 caused by the out-of-round head sheave should be considered because of resonance.

With reference to Fig. 1(b), the kinetic energy $T$ of hoisting cable can be expressed as:

1

T = \frac{1}{2} \int_{0}^{l (t)} [ρ {(\frac{D u}{D t} + v)}^{2} + J {(\frac{D θ}{D t})}^{2}] d x,

where $ρ$ and $J$ are the mass per unit length and moment of inertia of the hoisting cable.

The total potential energy $V$ of the system can be represented as:

2

V = \int_{0}^{l (t)} \frac{1}{2} [(Q_{1} ε + Q_{2} ϕ) ε + (Q_{3} ε + Q_{4} ϕ) ϕ] d x,

where $Q_{1}$ , $Q_{2}$ , $Q_{3}$ and $Q_{4}$ are the axial, axial-torsional coupling, torsional-axial coupling, and torsional stiffness coefficients of the hoisting cable, respectively. The approximation $Q_{23} = Q_{2} = Q_{3}$ will be adopted in the following derivation [7]. The strain $ε$ and $ϕ$ can be defined as $ε = u_{x}$ , $ϕ = θ_{x}$ . The virtual work is done by the interaction force $H$ can be expressed as:

3

δ W = - H \cdot δ u (l, t) = - m_{c} (\frac{D^{2} u}{D t^{2}} + a) \cdot δ u (l, t) .

As shown in Fig. 2, the whole hoisting cable is divided into a number of cable elements. Every cable element presented here consists of two nodes and each node has the axial displacement $u (x, t)$ and torsional deformation $θ (x, t)$ . It should be noted that the variable-length element [9] is adopted since the length of the hoisting cable varies with time. However, as opposed to the length, the number of elements $n$ remains constant.

Fig. 2Cable element

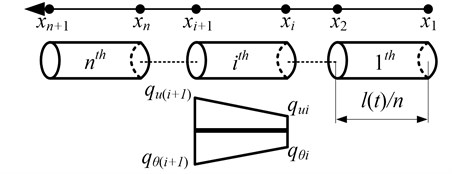
In the FEM, the cable displacements could be approximated by the discretized nodal displacements. Thus, the displacements of any point within the $i$ th element can be related to the discretized nodal displacement vectors $q_{u i}$ and $q_{θ i}$ as well as the shape function matrices $N_{i}$ as:

4

u (x, t) = N_{i} (x, l (t)) q_{u i} (t), θ (x, t) = N_{i} (x, l (t)) q_{θ i} (t),

where $q_{u i}$ and $q_{θ i}$ are the 2×1 nodal displacement vectors and given by $[\begin{array}{l} q_{u i} (t) & q_{u (i + 1)} (t) \end{array}]^{T}$ and $[\begin{array}{l} q_{θ i} (t) & q_{θ (i + 1)} (t) \end{array}]^{T}$ . $N_{i}$ is derived from the linear displacement of element and defined as:

5

N_{i} = [\frac{x_{i + 1} - x}{x_{i + 1} - x_{i}}, \frac{x - x_{i}}{x_{i + 1} - x_{i}}] = \frac{n}{l} [\frac{l}{n} i - x, x - \frac{l}{n} (i - 1)] .

Differentiating Eq. (5) with respect to $x$ and $t$ yields:

6

N_{i x} = \frac{n}{l} [- 1,1], N_{i t} = \frac{n v}{l^{2}} [x, - x], N_{i x t} = \frac{n v}{l^{2}} [- 1,1], N_{i t t} = (l a - 2 v^{2}) \frac{n}{l^{3}} [x, - x] .

Also, the variations of $u (x, t)$ and $θ (x, t)$ are expressed as:

7

δ u = δ q_{u i}^{T} N_{i}^{T}, δ θ = δ q_{θ i}^{T} N_{i}^{T}, δ u_{x} = δ q_{u i}^{T} N_{i x}^{T}, δ θ_{x} = δ q_{θ i}^{T} N_{i x}^{T} .

Substituting Eqs. (1)-(3) into the Hamilton’s principle and applying the variation operation can obtain that:

8

\int_{t_{1}}^{t_{2}} \sum_{i = 1}^{n} δ T_{i} d t = \int_{t 1}^{t_{2}} \sum_{i = 1}^{n} \int_{x_{i}}^{x_{i + 1}} \{ρ [(v^{2} + v u_{t} + v^{2} u_{x}) δ u_{x} - (a + u_{t t} + a u_{x} + v u_{x t}) δ u]

+ J [(v u_{t} + v^{2} u_{x}) δ θ_{x} - (u_{t t} + a u_{x} + v u_{x t}) δ θ]\} d x d t,

9

\int_{t_{1}}^{t_{2}} \sum_{i = 1}^{n} δ V_{i} d t = \int_{t 1}^{t_{2}} \sum_{i = 1}^{n} \int_{x_{i}}^{x_{i + 1}} [(Q_{1} u_{x} + Q_{23} θ_{x}) δ u_{x} + (Q_{23} u_{x} + Q_{4} θ_{x}) δ θ_{x}] d x d t .

The assembled global finite element equations are obtained:

10

[\begin{matrix} M_{u} & 0 \\ 0 & M_{θ} \end{matrix}] \{\begin{array}{l} {\ddot{Q}}_{u} \\ {\ddot{Q}}_{θ} \end{array}\} + [\begin{matrix} C_{u} & 0 \\ 0 & C_{θ} \end{matrix}] \{\begin{array}{l} {\dot{Q}}_{u} \\ {\dot{Q}}_{θ} \end{array}\} + [\begin{matrix} K_{u} & K_{u θ} \\ K_{θ u} & K_{θ} \end{matrix}] \{\begin{array}{l} Q_{u} \\ Q_{θ} \end{array}\} = \{\begin{array}{l} F_{u} \\ F_{θ} \end{array}\},

where $Q$ is the vector of generalized coordinates; $M$ , $C$ , $K$ and $F$ are the mass, damping, stiffness matrices and the force vector, respectively. Entries of these matrices are expressed as:

11

M_{u} = \sum_{i = 1}^{n} {m_{u}}_{i} = \sum_{i = 1}^{n} ρ \int_{x_{i}}^{x_{i + 1}} N_{i}^{T} N_{i} d x,

C_{u} = \sum_{i = 1}^{n} {c_{u}}_{i} = \sum_{i = 1}^{n} ρ \int_{x_{i}}^{x_{i + 1}} (2 N_{i}^{T} N_{i t} + v N_{i}^{T} N_{i x} - v N_{i x}^{T} N_{i}) d x,

K_{u} = \sum_{i = 1}^{n} {k_{u}}_{i} = \sum_{i = 1}^{n} \int_{x_{i}}^{x_{i + 1}} [ρ (N_{i}^{T} N_{i t t} + a N_{i}^{T} N_{i x} + v N_{i}^{T} N_{i x t} - v N_{i x}^{T} N_{i t} - v^{2} N_{i x}^{T} N_{i x})

+ Q_{1} N_{i x}^{T} N_{i x}] d x,

K_{u θ} = K_{θ u} = \sum_{i = 1}^{n} {k_{u}}_{θ}_{i} = \sum_{i = 1}^{n} \int_{x_{i}}^{x_{i + 1}} Q_{23} N_{i x}^{T} N_{i x} d x,

F_{u} = \sum_{i = 1}^{n} {f_{u}}_{i} = \sum_{i = 1}^{n} \int_{x_{i}}^{x_{i + 1}} ρ (v^{2} N_{i x}^{T} - a N_{i}^{T}) d x, F_{θ} = 0 .

Similarly, $M_{θ}$ , $C_{θ}$ and $K_{θ}$ can be gained by replacing $ρ$ and $Q_{1}$ in Eq. (11) with $J$ and $Q_{4}$ , respectively. Especially:

{M_{u}}_{(n, n)} = {(ρ \int_{x_{n}}^{x_{n + 1}} N_{i}^{T} N_{i} d x)}_{(2,2)} + m_{c}, F_{u (1)} = {M_{u}}_{(1,1)} [a (t) + e (t)] .

3. ADAMS simulation modeling

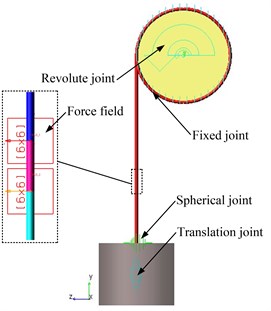
The dynamics simulation model based on multi-degree of freedom is established using the ADAMS software package, as is illustrated in the Fig. 3. This model mainly aims at simulating the coupled dynamic responses of the hoisting cable and verifying the finite element model. The hoisting cable is discretized into a certain amount of cylinders, which are connected with the force field. The rigid cylinders are wound around the head sheave by the fixed joint. The hoisting mass is connected to the lower end of the cable by the spherical joint and the head sheave is installed on the ground by the revolute joint, then the translation joint is employed to longitudinal axis. The driving strategy is that the fixed joint will cooperate with the distance sensor under the control of script [10].

Fig. 3ADAMS simulation model

4. Results and discussion

Consider a hoisting cable with $ρ =$ 0.4 kg/m, $Q_{1} =$ 3.46×10⁷ N, $Q_{23} =$ 1.2×10⁵ N∙m and $Q_{4} =$ 660 N∙m². The Moment of inertia $J$ and Hoisting mass $m_{c}$ are 2×10^-5 kg∙m and 2000 kg. The total length $L$ of the hoisting cable is 244 m and the initial length $l (0)$ is 4 m. The vertical excitation applied to the head sheave is $e (t) = 0.003 s i n (2 π t)$ m. The maximum velocity and acceleration are 6 m/s and 2 m/s², respectively. In the ADAMS simulation, the hoisting cable is discretized into 610 cylinders. The total simulation time is 50 s and the time step size is 0.01 s. The element number is $n =$ 30.

In order to validate the finite element model using the simulation results obtained from the ADAMS model, the axial and the torsional displacements of the lower end of the cable in both simulations are analyzed. The comparisons are shown in Fig. 4.

Fig. 4a) Comparisons on the axial and b) torsional displacements

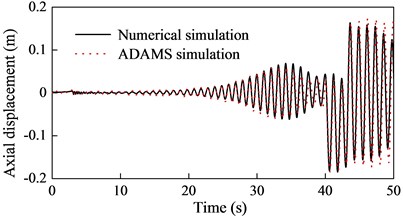
a)

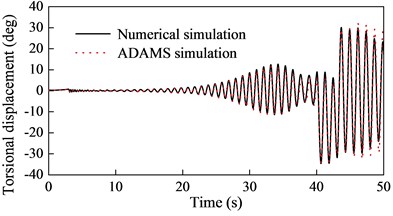
b)

Fig. 4 shows that the numerical simulations are in reasonably good agreement with the ADAMS simulations, which confirms the validity of the finite element model. The curves demonstrate the longitudinal and torsional resonances in the system occur simultaneously.

In the following, the excitation frequency will be increased to 2 Hz, and then the longitudinal vibration of the lower end of the cable will be investigated with $Q_{23} =$ 0 in case 1, $Q_{23} =$ 0.9×10⁵ in case 2 and $Q_{23} =$ 1.2×10⁵ in case 3. The results are shown in Fig. 5.

Fig. 5Longitudinal vibration with different Q23

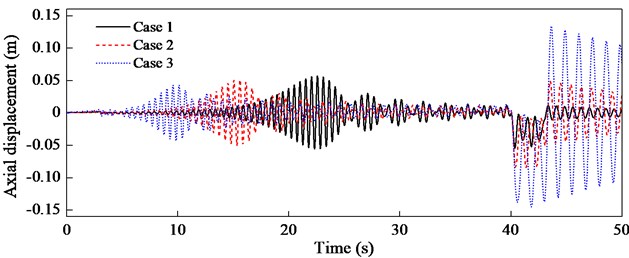
Fig. 5 indicates both the resonance frequency and the maximum amplitude with different $Q_{23}$ are entirely different, which proves that the coupling effect of the cable itself has a great influence on the longitudinal vibration. Therefore, the coupling effect should be considered in practice for the accurate response prediction and vibration control. The resonance of the cable in case 2 occurs earlier than that in case 1 and later than case 2, which reveals that the coupling effect reduces the longitudinal natural frequency of the cable. In case 1 the maximum amplitude occurs at the deceleration stage while in case 3 it appears in the resonance region, which implies that the maximum amplitude will shift from the resonance region to the deceleration stage as the coupling coefficient increases. Besides, the major reason accounting for such large amplitude in case 3 is that the strand of cable will become looser or tighter when the cable is subjected to axial loading only, which mainly contributes to the additional length change.

5. Conclusions

The coupled axial-torsional responses of the hoisting cable with time-varying length are investigated in aspects of both theory and ADAMS simulation. The theoretical model of the coupled axial-torsional vibrations of the hoisting cable is established using the FEM with a variable-length element. An ADAMS simulation model is established in order to validate this theoretical model. The result shows that the numerical simulation is in reasonably good agreement with the ADAMS simulation. The analysis on the frequency of the cable indicates the coupling effect reduces the natural frequency of the cable and the maximum amplitude shifts from the resonance region to the deceleration stage as the coupling coefficient increases.

References

Ma C., Xiao X. M. Kinetic analysis of a multi-rope friction mine hoist under overload conditions. Journal of Vibroengineering, Vol. 15, Issue 2, 2013, p. 925-932.

Search CrossRef
Zi B., Qian S., Ding H. F., Andres K. Design and analysis of cooperative cable parallel manipulators for multiple mobile cranes. International Journal of Advanced Robotic Systems, Vol. 9, 2012, p. 1-10.

Search CrossRef
Zhu W. D., Ren H. A linear model of stationary elevator traveling and compensation cables. Journal of Sound and Vibration, Vol. 332, Issue 12, 2013, p. 3086-3097.

Search CrossRef
Wang P. H., Fung R. F., Lee M. J. Finite element analysis of a three-dimensional underwater cable with time-dependent length. Journal of Sound and Vibration, Vol. 209, Issue 2, 1998, p. 223-249.

Search CrossRef
Kaczmarczyk S., Ostachowicz W. Transient vibration phenomena in deep mine hoisting cables. Part 1: mathematical model. Journal of Sound and Vibration, Vol. 262, Issue 2, 2003, p. 219-244.

Search CrossRef
Zhang P., Zhu C. M., Zhang L. J. Analysis of forced coupled longitudinal-transverse vibration of flexible hoisting system with varying length. Engineering Mechanics, Vol. 25, Issue 12, 2008, p. 202-207.

Search CrossRef
Samras R. K., Skop R. A., Milburn D. A. Analysis of coupled extensional torsional oscillations in wire rope. Journal of Engineering for Industry, Vol. 96, 1974, p. 1130-1135.

Search CrossRef
Hashemi S. M., Roach A. A dynamic finite element for vibration analysis of cables and wire ropes. Asian Journal of Civil Engineering, Vol. 7, Issue 5, 2006, p. 487-500.

Search CrossRef
Du J. L., Cui C. Z., Bao H., Qiu Y. Y. Dynamic analysis of cable-driven parallel manipulators using a variable length finite element. Journal of Computational and Nonlinear Dynamics, Vol. 10, Issue 1, 2015, p. 011013.

Search CrossRef
Wang J. J., Cao G. H., Wang Y. D., Wu R. H. A novel driving strategy for dynamic simulation of hoisting rope with time-varying length. International Journal of Modeling, Simulation, and Scientific Computing, Vol. 4, Issue 3, 2013, p. 1350009.

Search CrossRef

About this article

Received

Accepted

25 September 2015

Published

09 October 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

hoisting cable

coupled vibration

finite element method

ADAMS simulation

Acknowledgements

This work is supported by the National Natural Science Foundation of China (51475456), Program for New Century Excellent Talents in University (NCET-13-1017) and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.