Topology optimization for vibrating structures with the BESO method

1. Introduction

Structural optimization seeks to achieve the best performance for a structure while satisfying various constraints such as a given amount of material [1]. In recent decades, structural optimization methods have gained great progress with the increasing performance of computers and computing algorithms [2]. Structural optimization methods can be classified into three categories: sizing optimization, shape optimization and topology optimization [3]. Compared with other types of structural optimization, topology optimization of continuum structures is by far the most challenging technically [1]. Different types of topology optimization methods exist. As an important subtype, the evolutionary structural optimization (ESO) method was initially proposed by Xie and Steven based on a simple concept that a structure evolves towards an optimum by gradually removing less stressed material [4]. Yang expanded the ESO method to bi-directional evolutionary structural optimization (BESO) method allowing the recovery of the deleted elements which are neighboring to highly stressed elements [5]. In 2007, Huang and Xie improved the BESO method with a sensitivity filter scheme and a stabilization scheme using the history information [6], which is the latest major update for the BESO method. The latest version of BESO method includes the following procedure [6]: 1) Discretize the design domain using a finite element mesh; 2) Perform finite element analysis and then calculate the smoothed elemental sensitivity number; 3) Average the sensitivity number with its history information; 4) Determine the target volume for the next iteration; 5) Add and delete elements according to the sensitivity number; 6) Repeat steps 2-5 until the constraint volume is achieved.

The BESO method has been used in several static optimization problems, but it is not widely used in dynamics problems. Possible reasons for this are the computation complexity and the possible deletion of load regions.

In this paper, we propose the von Mises stress as a sensitivity number and a new filter scheme for the BESO method focusing on dynamics problems, and use it with a commercial Finite Element Analysis (FEA) software to implement the dynamics topology optimization. We will use the presented methods for the large-scale 3D topology optimization for machine tools in the future.

The organization of the paper is as follows: in Section 2, we define the use case and propose two vibration reduction measures. In Section 3, we clarify the selection of the sensitivity number for the BESO method and the new filter scheme. Based on Section 2 and Section 3, we implement the two measures and present one numerical example in Section 4 and 5. In Section 6, we give a brief comparison between proposed BESO methods in this paper and existing evolutionary methods (ESO and BESO). We present the conclusions from this study in Section 7.

2. Dynamics optimization problem under a single external harmonic loading

In many industrial use cases, especially in the machine tool industry engineers want to reduce the vibration amplitude at a user-defined point. This paper discuss two measures to achieve this goal for structures under a single external harmonic loading. The NFBM shifts the natural frequency of the most significant mode away from the driving frequency, while the SSDBM consider several modes and natural frequencies at the same time using modal superposition.

3. Sensitivity number and filter scheme

The basic idea of the BESO method is to remove the unnecessary material from the structure. A reliable indicator of the inefficient use of material is a low value of stress in some parts of the structure. Nowadays, the distortion energy theory for ductile material uses the von Mises stress as an equivalent or effective stress to indicate the stress level of a continuum element within a structure under the three-dimensional loading [7]:

The von Mises stress has been applied with the BESO method for static problems [8]. In this paper, the von Mises stress is used with the BESO method to indicate the inefficient use of material under dynamic loading.

Most of all BESO is a hard kill method, which means one element can only be solid or void and not have intermediate densities. This property is one of the most important advantages of the BESO method, which saves much computation time. But it can also cause a serious problem: sometimes it removes the elements, which transmit external loads into the structure. In order to avoid this problem, we propose a new filter scheme for the sensitivity number:

where ${\sigma }_{si}^{\text{'}}$, ${\sigma }_{s\_max}^{\text{'}}$ and ${\stackrel{-}{\sigma }}_{si}^{\text{'}}$ are the von Mises stress for the $i$th element, the maximum of von Mises stress, and the normalized von Mises stress for the $i$th element in static simulation. ${\sigma }_{di}^{\text{'}}$, ${\sigma }_{d\_max}^{\text{'}}$ and ${\stackrel{-}{\sigma }}_{di}^{\text{'}}$ are the von Mises stress for the $i$th element, the maximum of von Mises stress and the normalized von Mises stress for the $i$th element in dynamics simulation. ${\alpha }_i$ is the sensitivity number for $i$th element, $w$ is the weighting factor of the static simulation, $1-w$ is the weighting factor of the dynamics simulation, $r_i$ is the distance between centroid of the $i$th element and the load point, and $p$ is the distance penalty factor. The influence of the distance $r_i$ increases with the $p$, where $p$ is not smaller than 0. This filter scheme can be expanded to multiple loading points.

We take the dynamics analysis, static analysis and the position of the load point into account with this filter scheme. The influences of the static analysis and the position of the load point depend on the weighting factor $w$ and the distance penalty factor $p$.

4. Vibration reduction measures

5. Numerical example

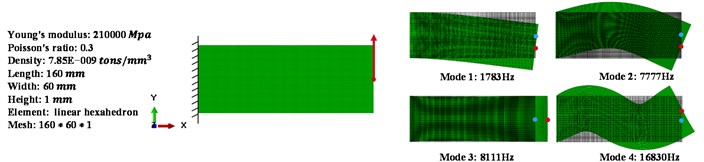
We present one numerical example to show the effect of those two measures. The example is a traditional 3D cantilever beam as shown in Fig. 1. The external harmonic load excites the beam at the middle point of the right edge with a driving frequency of 7500 Hz. The target volume is 70 % of the design domain. The objective is to minimize the vibration amplitude in $Y$-direction at the load point. We calculate the vibration amplitude at the load point in the mode-based steady state dynamics analysis, which considers the first 10 modes in this example. We set the above proposed weighting factor of the static simulation $w$ as 0.1 and the distance penalty factor p as 0.5 (see Eq. (2)).

The first four modes before the optimization process are shown in Fig. 1.

Fig. 1Design problem for the example

5.1. Vibration reduction with the NFBM

Mode 2 and 3 are both significant modes, because their natural frequencies are near the driving frequency. In order to pick the most significant one, we observe these two mode shapes as shown in Fig. 1. The displacement of load point in mode 2 is mainly in $Y$-direction whereas in mode 3 is mainly in $X$-direction. Because we only consider the vibration in $Y$-direction in our example, the mode 2 is most relevant.

Fig. 2 shows the optimization history with the NFBM. In the first ten iterations, the displacement at load point reduces obviously, because the natural frequency of mode 2 increases and therefore moves away from the driving frequency. The second natural frequency still increases after 10 iterations, but the fourth natural frequency decreases dramatically, the displacement of the load point in mode 4 is also mainly in $Y$-direction, so the vibration reduction effect is compensated. The displacement starts to increase after 16 iterations, which means the total influence of other 9 modes has suppressed the influence of the second mode. As shown in (d) of Fig. 2, the mode 2 moves away from the driving frequency, while another significant mode moves closer. The most significant mode could change after the turnover point, which is shown in (b) of Fig. 2.

Fig. 2Optimization history: a) frequency, b) displacement, c) topology history, d) FRF

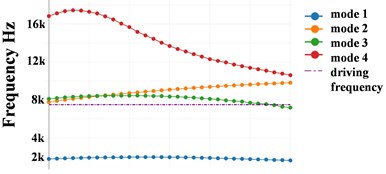
a)

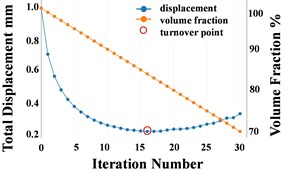
b)

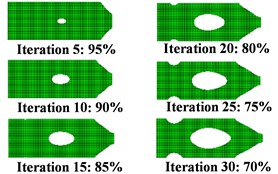
c)

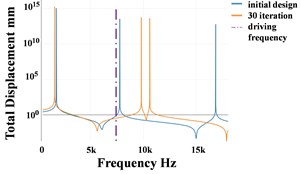
d)

5.2. Vibration reduction with the SSDBM

Fig. 3 shows the optimization history with the SSDBM. We can see clearly, the displacement at load point keeps decreasing for 30 iterations. Because this measure considers not only the most significant mode 2, but also other 9 modes. As shown in Fig. 3, the second natural frequency increases more slowly as in the NFBM, but mode 1 is pushed away from the driving frequency and the mode 4 approaches the driving frequency slower than with the NFBM. The synergy effect of the changes of all natural frequencies contribute to the continuous minimization of the vibration at the load point.

The vibration reduction slows with the increasing iteration number. The reason for this is: one can’t reduce the vibration and the amount of structure material at the same time with no limit.

Fig. 3Optimization history: a) frequency, b) displacement, c) topology history, d) FRF

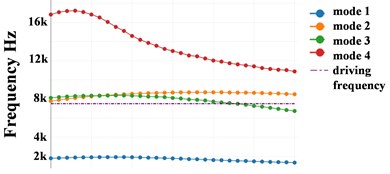
a)

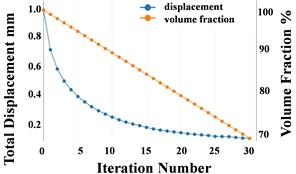
b)

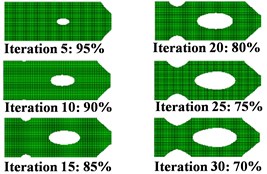
c)

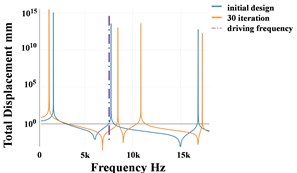
d)

6. A brief comparison with existing ESO and BESO methods

Xie and Steven used a hard-kill ESO method for dynamics optimization problems in 1990s [10]. They calculated the sensitivity number for each element as follows:

where ${\alpha }_i$, $m_i$, $u_i^e$, ${\omega }_i$ are the elemental sensitivity number, the modal mass, the elemental eigenvector and the corresponding natural frequency. $M^e$ and $K^e$ are the elemental mass matrix and the elemental stiffness matrix [10].

In order to avoid the direct deletion of elements, Huang has developed a new soft-kill BESO method for dynamics optimization problems in 2010 [11]. The sensitivity number is expressed as follows:

where ${\omega }_i$ and $u_i^e$ are the same as in Eq. (4). $x_i$, $x_{min}$ are the elemental density and the lower limit of the density, $p$ is the penalty factor, $K_i^1$ and $M_i^1$ are the elemental stiffness matrix and the elemental mass matrix for the stiffer element [11].

As shown in Eqs. (4), (5), the sensitivity number of these two existing methods depends on the elemental mass matrix and the elemental stiffness matrix, which means that the calculation of the sensitivity number is much more expensive than in this paper, and it takes place outside the commercial FEM software.

Furthermore, these existing methods can only directly use the natural frequency as the optimization target. To the best of my knowledge, there is no existing ESO or BESO method concerning directly about the vibration reduction at a use-defined point of structures under a harmonic loading, while the SSDBM proposed in this paper use the vibration amplitude at a user-defined point directly as the optimization target. Additionally, the NFBM and the SSDBM take the influence of the load position into account at the same time.

7. Conclusions

This paper presents the von Mises stress as a sensitivity number and a new filter scheme for the BESO method focusing on dynamics topology optimization problems. The new filter scheme takes the static analysis, dynamic analysis and load position into account at the same time. Based on the extended BESO method, we propose two measures to reduce the vibration and demonstrate them with two numerical examples. Examples have shown that these two measures are effective for structures subjected to a single external harmonic loading, and that the vibration reduction effect of the SSDBM is better than the NFBM. Furthermore, the SSDBM does not need the MAC mode tracking technique, which saves computation time compared to the NFBM.

The calculation of the von Mises stress is not computationally expensive and takes place within the commercial FEA software. Furthermore, the BESO method reduces the FEM problem size after every iteration. Because of these advantages, these two proposed measures are very efficient from the aspect of computation time. We will extend these two measures in the future research, in order to make it suitable for large-scale FEM-meshes.