Damage identification using singular value feature of continuous wavelet coefficients

1. Introduction

Structural damage detection has gained increasing attention throughout civil, mechanical, and aerospace engineering communities [1-3]. In recent years, various damage identification methods have been developed, typically vibration-based methods, wave propagation-based methods, and the methods stemming from the interaction of multiple disciplines [4-6]. Especially, soft computing approaches have been increasingly used to detection structural damage and on this basis, soft computing-based damage identification is becoming an active research focus. The prevailing soft computing methods present in structural damage detection studies include neural networks [7, 8], wavelet transforms (WT) [9, 10], genetic algorithms [11, 12], singular value decomposition (SVD) [13-19], fuzzy logic [20-21] etc. Among the existing soft computing methods mentioned above, SVD and WT are two interesting soft computing methods. In general they are individually employed to identify structural damage, while taking on dissimilar functions of damage characterization due to the different properties of their own. However, there is literature in computer science which shows that hybridizing two or more soft computing methods can result in improved damage detection systems [22-24].

In this paper, an approach is formulated based on integration of two renowned soft computing methods: a wavelet transform and a singular value decomposition. The integration features the creation of a sophisticated damage indicator: Mode shape’ continuous Wavelet transform-Singular value decomposition Component (MWSC).

2. Damage indicator: MWSC

Let $W$ be a 1D displacement mode shape of a structural beam component. The continuous wavelet transform (CWT) of $W$ is expressed as:

where $W_{u,s}$ is the CWT coefficient of $W$ in space-scale domain with respect to wavelet $\mathrm{\Psi }$; $s$ and $u$ are the scale (or dilation) and space (or translation) parameters, respectively. Unlike the 1D mode shape $W\text{,}$$W_{u,s}$ is a 2D matrix of continuous wavelet coefficients (CWC) with the dimensions of the matrix are measured by the numbers of the discretized $u$ and $s$ in the $u$ and $s$ directions, respectively. $W_{u,s}$ can be analyzed by the SVD, giving as:

where $u$, $s$ jointly indicate the data originating from the CWC field. The columns of $U_{u,s}$ are the left singular vectors $\left\{u_k^{u,s}\right\}$, and the columns of $V_{u,s}^T$ are the right singular vectors $\left\{v_k^{u,s}\right\}$. ${\sigma }_1^{u,s}\ge {\sigma }_2^{u,s}\ge \cdots \ge {\sigma }_r^{u,s}\ge 0$ of $S_{u,s}$ give the singular values of $W_{u,s}$. $W_{u,s}$ can also be expressed as the summation of its singular components:

where $u_k^{u,s}{v_k^{u,s}}_{}^T$ is the $k$th singular component of $W_{u,s}$. $W_{u,s}^{wsc}=u_k^{u,s}{v_k^{u,s}}_{}^T$, defines a new damage indicator: Mode shape’ continuous Wavelet transform-Singular value decomposition Component.

3. Numerical verification

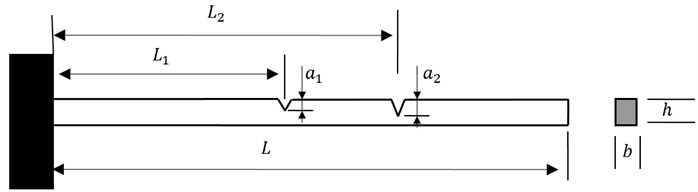
The use of the damage indicator, MWSC, to identify damage is numerically verified by an Euler-Bernoulli cantilever beam with multiple single-sided through-width transverse cracks. The finite element of a cantilever beam with double cracks is created, shown in Fig. 1. The beam has dimensions: length $L=$ 500 mm, width $B=$ 50 mm, height $H=$ 10 mm. Elastic modulus, Poisson’s ratio, and material density are taken as 206 GPa, 0.3, and 7860 kg/m³, respectively. The depth ratio is noted as $\xi =a/h$, $a$ being the crack depth and $h$ is the height of the beam cross-section. Two cracks are located at 125 mm (${\zeta }_1=\mathrm{}$0.25) and 325 mm (${\zeta }_2=\mathrm{}$0.65), with depths 2 mm and 3 mm, respectively.

The finite element equation of a beam segment based on the Euler-Bernoulli theory of length $\mathrm{\Delta }L$ can be defined as [25]:

where matrices ${\left[M\right]}_e$ and ${\left[K\right]}_e$ are the elemental mass and stiffness matrices defined as:

and ${\left\{f\right\}}^e$ is the generalized element load vector. $E$, $I$, $A$ and $\rho$ are Young’s modulus, moment of inertia, cross-section area and material density, respectively. The crack is modeled as a linear rotational spring [26-29]. After application of the boundary conditions, the characteristic equation for the free vibration of the beam can be described as:

where $\left[K\right]$ and $\left[M\right]$ are the global stiffness and mass matrices. Solving Eq. (6) yields the natural frequency $\omega$ and $W_i$ denoting the obtained $i$th-order mode shape.

Fig. 1A cantilever Euler-Bernoulli beam with double cracks

4. Damage identification

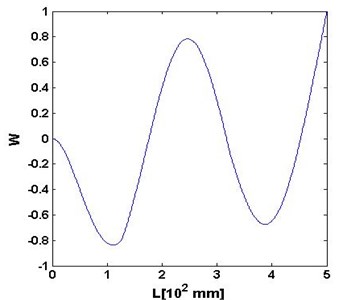
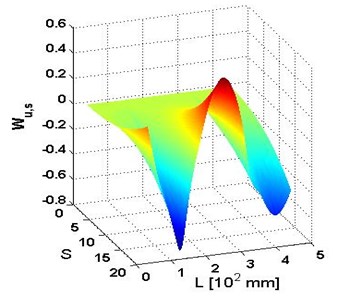
The mode shape, $W_4$, (Fig. 2(a)) is arbitrarily chosen to demonstrate the capability of the MWSC to detect damage. The mode shape looks fairly smooth, from which no any damage signature can be discerned. The mode shape is processed by the CWT in terms of Eq. (1) to produce $W_{u,s}$, with the result shown in Fig. 2(b). In Fig. 2(b), $W_{u,s}$ for $W_4$ appears an regular and flowing surface of the global trend of $W_{u,s}\text{,}$ with the possible damage feature entirely overshadowed by the trend. The instance indicates that the use of CWT for damage detection may undergo a particular problem of the global fluctuating trend usually concealing the damage feature.

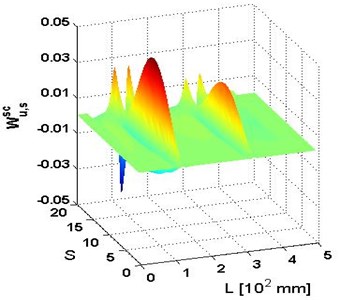
Fig. 2a) W, b) Wu,s, c) Wu,ssc and d) planform of Wu,ssc for the 4th mode shape

a)

b)

c)

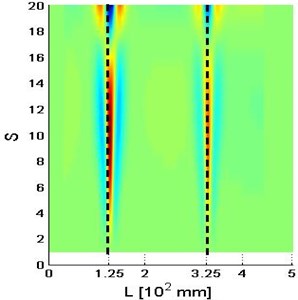
d)

Among singular components, the combination of the 2nd and 3rd singular component, $W_{u,s}^{sc}$, are selected to form the damage indicator, MWSC. The resulting MWSC is shown in Fig. 2(c)-(d) corresponding to the 4th mode shape. Dramatically, in the figure, $W_{u,s}^{sc}$ bears two pronounced peaks that sharply stand out of the rest area of $W_{u,s}^{sc}$. These peaks purely characterize the damage information by getting rid of the global trend influence, undoubtedly designating the occurrence and location of cracks. The two vertical lines in the planform of $W_{u,s}^{sc}$ distinctly delineate the location of the cracks at 125 mm (${\zeta }_1=\mathrm{}$0.25) and 325 mm (${\zeta }_2=\mathrm{}$0.65) distances, respectively. The superiorities of $W_{u,s}^{sc}$ over $W_{u,s}$ to reflect damage indicates that the integration of CWT and SVD provides a valid regime of damage identification; in particular, the SVD plays a critical role of extracting damage feature.

5. Robustness against noise

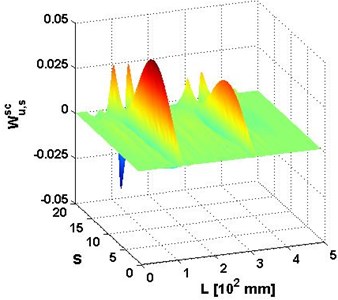
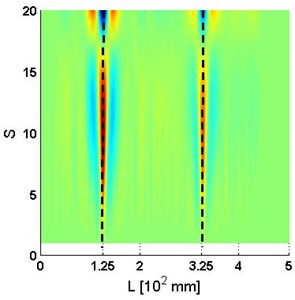
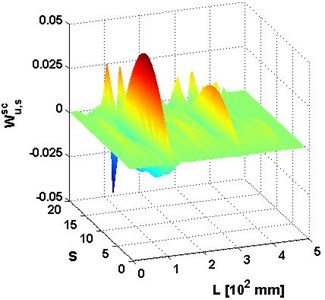
The capability of damage indicator, MWSC, to identify damage in noisy environment is investigated using $W_4$ with added noise at various signal-to-noise ratios (SNRs). The white Gaussian noise is incorporated into the modal data by the Matlab function $y_n=awgn\left(y_0,\mathrm{s}\mathrm{n}\mathrm{r}\right)$, where $y_0$ and $y_n$ denote noise-free and noisy data, respectively. Noises of various SNRs ranging from 60 dB to 40 dB with a step of 2.5 dB are individually added to $W_4$ to simulate the 4th mode shape obtained by actual measurement. Following the procedure provided in Eq. (1) and Eq. (3), the representative outcomes of $W_{u,s}^{sc}$ are presented in Figs. 3-5 for SNRs equal to 60 dB, 50 dB, and 40 dB, respectively.

Fig. 3a) Wu,ssc and b) planform of Wu,ssc for the 4th mode shape with SNRs = 60 dB

a)

b)

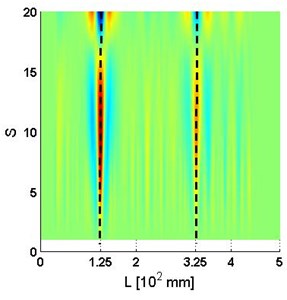
Fig. 4a) Wu,ssc and b) planform of Wu,ssc for the 4th mode shape with SNRs = 50 dB

a)

b)

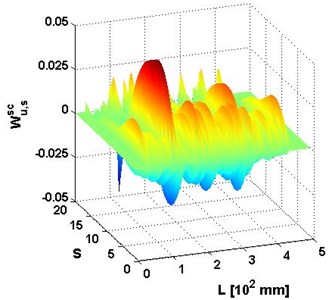
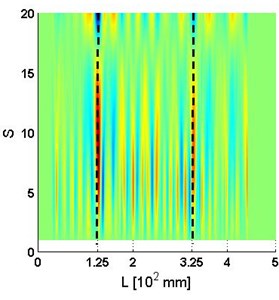
In general, for the cases where the SNRs is not less than 50 dB, the identification results are similar to the result of the case without noise (Figs. 2(c)-(d)), with two sharp peaks distinctly indicating double cracks. For the case with the SNRs equal to 40 dB, the peak for the crack at 125 mm is still noticeable; however the peak for the crack at 325 mm is obscured by the noise.

Fig. 5a) Wu,ssc and b) planform of Wu,ssc for the 4th mode shape with SNRs = 40 dB

a)

b)

6. Conclusions

In the field of structural health monitoring, identification of multiple damages is an issue of wider significance and of greater challenge compared to single damage identification. As an exploration for multiple-damage identification in beams, this study using a hybrid soft computing approach develops MWSC, assimilating the complementary merits of the SVD and WT in portraying damages in beams. The effectiveness of the MWSC is numerically verified by identifying multiple cracks in cantilever beams. Numerical results show that the MWSC features stronger immunity to noise and greater sensitivity to damage in comparison to the individually employed CWT technique.