Automated wavelet-based damage identification in sandwich structures using modal curvatures

Katunin, Andrzej; Przystałka, Piotr

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2015

Check for updates

Automated wavelet-based damage identification in sandwich structures using modal curvatures

Andrzej Katunin¹

Piotr Przystałka²

^{1, 2}Institute of Fundamentals of Machinery Design, Silesian University of Technology, Gliwice, Poland

Corresponding Author:

Andrzej Katunin

Cite the article Download PDF

Downloads 1118

Abstract

Recently, damage assessment of composite structures being in operation has been one of crucial problems in industries such as aircraft, aerospace, automotive, etc. Following this, rapid development of non-destructive testing methods has been observed over the last decades. One of the promising approaches is vibration-based one, which in general is based on identification of a damage using singularities in modal shapes of vibration. The identification procedure requires application of advanced signal processing techniques, where the wavelet transform is used the most commonly. Due to the high sensitivity of wavelet-based approach to changes of parameters of an analysis, e.g. a type of applied wavelet and its order, it was decided to develop an algorithm, which allows automating this process by using multi-objective meta-optimization of the mentioned parameters. The presented approach allows selecting optimal parameters for wavelet-based damage identification procedure without neither a priori knowledge on values of wavelet parameters, nor the parameters of an optimization algorithm. The proposed approach was tested on composite sandwich structures with damaged core as well as damaged face sheets. Obtained results confirm the effectiveness of automated damage identification mainly in the context of the high convergence to the optimal solution.

1. Introduction

Considering a fact that composites are more and more applicable in various branches of industry the appropriate maintenance strategies should be applied for structural elements made of these materials. One of the crucial elements in such strategies is an evaluation of structural integrity and operational lifetime, in particular damage assessment. A special type of composite structures – sandwich structures – has found a wide application in construction of vehicles, mainly in aircraft, aerospace and marine industries, due to its excellent stiffness-to-mass ratio. Due to the specific lay-up of sandwich structures, which consist a stiff core made of foam or formed in the lattice configuration (rectangular lattice, honeycomb lattice, etc.), and face sheets usually made in the form of polymeric laminates, the damage, which may appear both during manufacturing as well as during operation of such structures, may have various characters. A possible damage of such structures includes cracking of a core and face sheets, delamination of face sheets and delamination on the interface of a core and face sheets, etc. Following this, the appropriate damage assessment procedures, which allow for identification of mentioned types of damage, should be established.

From a variety of to-date developed non-destructive testing (NDT) methods one of intensively advanced groups of methods is a group of vibration-based NDT methods. The vibration-based approach is based on evaluation of modal shapes of vibration using advanced signal processing methods, which allow detecting and localizing small singularities in modal shapes caused by local stiffness reduction in a damaged region of an analyzed structure. One of the most promising approaches is the wavelet-based analysis of modal shapes, which has gained a popularity over last two decades. This approach was used in several numerical and experimental studies, where various wavelet-based algorithms were applied, e.g. in [1-4]. However, these approaches suffer the major drawback of wavelet-based algorithms: the detectability of a damage and accuracy of its localization and identification strongly depends on an applied wavelet transform and parameters of an applied wavelet, e.g. its type, order, effective support, etc. Several attempts were made in order to evaluate the best wavelets for structural damage identification (SDI) problems [5, 6], however there is still no universal rule for selection of wavelets in such problems since wavelets and their parameters are problem-dependent. In order to avoid this drawback hybrid algorithms have become to be developed. In particular, the authors of [7-9] used hybrid algorithms, which are based on a combination of wavelet transform and artificial neural networks, the authors of [10] performed a hybridization of wavelet-based algorithms with multi-objective optimization ones.

Similar hybridization approach was developed by the authors in recent years. The first study [11] is based on selection of optimal parameters of fractional B-spline wavelet in order to improve damage identification in beam-like structures. Further, the algorithm was extended to 2D problems and verified both on numerical and experimental data [12]. This approach allows for selection of optimal values of applied fractional B-spline wavelets, however selection of parameters of an optimization algorithm is necessary to obtain these optimal values. In order to avoid selection of these parameters the authors proposed a meta-optimization approach [13] with initial verification studies on numerical and experimental data.

The results obtained in the latter study induced the authors of this paper to improve the proposed approach by construction of more effective and robust cost function and evaluation of wavelet coefficients obtained from fractional wavelet decomposition based on its energy amount.

2. Method of automated damage identification in sandwich structures

2.1. Wavelet-based signal processing

At the first stage of the proposed algorithm the 2D signals (modal shapes of vibration) are subjected to a single-level fractional wavelet transform (FrWT) introduced by Unser and Blu [14]. The decomposition procedure is performed using $α$ , $τ$ -B-spline wavelets, where $α$ is a fractional order and $τ$ is a shift parameter, both defined as reals. The general order $α$ , $τ$ -B-spline scaling functions are defined as:

1

β_{τ}^{α} (x) = \sum_{k = 0}^{\infty} {(- 1)}^{k} |\begin{array}{l} α + 1 \\ k - τ \end{array}| ρ_{τ}^{α} (x - k),

where:

2

ρ_{τ}^{α} (x) = - \frac{c o s π τ}{2 Γ (α + 1) s i n (π α / 2)} {|x|}^{α} - \frac{s i n π τ}{2 Γ (α + 1) c o s (π α / 2)} {|x|}^{α} s g n (x),

and $Γ (α + 1)$ is the Euler’s gamma function, which is defined as:

3

Γ (α + 1) = \int_{0}^{\infty} x^{u - 1} e^{- x} d x .

They hold a two-scale relation [15]:

4

\frac{1}{2} β_{τ}^{α} (\frac{x}{2}) = \sum_{k \in Z} h_{τ}^{α} [k] β_{τ}^{α} (x - k),

where $h_{τ}^{α} [k]$ is a refinement filter.

The B-spline wavelets $ψ_{τ}^{α}$ of fractional order also hold a two-scale relation [14]:

5

ψ_{τ}^{α} (\frac{x}{2}) = \sum_{k \in Z} 2^{- α} {(- 1)}^{k} \sum_{l \in Z} (\begin{matrix} α + 1 \\ l \end{matrix}) β_{0}^{2 α + 1} (l + k - 1) β_{τ}^{α} (x - k) .

In order to improve directional selectivity of these wavelets in 2D domain Chaudhury and Unser [15] proposed a complexification procedure:

6

ψ_{τ}^{α} (x) = ψ_{τ}^{α} (x) + j ψ_{τ + 1 / 2}^{α} (x),

and representing wavelets in the form of Hilbert transform pairs:

7

ψ_{α} (x) = ψ + j H \{ψ\} .

This allows obtaining 6 direction-oriented 2D complex wavelets:

8

ψ_{1} (x, y) = ψ_{α} (x) β (y), ψ_{2} (x, y) = ψ_{α} (x) H β (y), ψ_{3} (x, y) = β (x) ψ_{α} (y),

ψ_{4} (x, y) = H β (x) ψ_{α} (y), ψ_{5} (x, y) = 2^{- 1 / 2} ψ_{α} (x) ψ_{α} (y), ψ_{6} (x, y) = 2^{- 1 / 2} ψ_{α}^{*} (x) ψ_{α} (y),

which are applied to an analyzed signal. From obtained 6 sets of complex coefficients the real values are determined and added up for better visual representation of identified singularities in particular directions. This approach is described in detail in [12].

2.2. Optimization method

As it was mentioned in the introduction section, the authors developed and successfully applied a soft computing method for tuning either parameters of fractional B-spline wavelet or behavioral parameters of an optimization engine [13]. However, the related approach was not satisfactory due to the assumed criteria which did not guarantee the unsupervised computations without any end-user’s interferences. The novelty in this study consists in the fact that there is no need to have a priori experimental knowledge by the user on parameters values of the proposed damage identification procedure.

The idea of the meta-optimization algorithm corresponds directly to the scheme presented in [13]. This strategy is adopted for searching the space of behavioral parameters of the target optimization algorithm. The meta-optimization algorithm (MAC) evaluates a meta-objective function, while the main optimization algorithm (OAE) calculates the cost function in order to reach an optimal solution with the minimum time complexity and maximum accuracy. The multi-objective function of the MAC can be formulated as follows:

9

C (b) = [\begin{array}{l} O b j_{1} (b) & O b j_{2} (b) \end{array}],

where $b$ is the set of behavioral properties of the OAE algorithm. The ﬁrst criterion corresponds to the estimation of the accuracy of a solution, whereas the second one represents the time computational complexity of the main optimization algorithm. It is assumed that these objectives are not conﬂicted, hence the multi-objective meta-optimization problem can be stated as the minimization task subjected to boundaries and constraints $Ω (b)$ .

The accuracy of the solution that is computed by the OAE can be estimated taking into account the mean value and the corrected sample standard deviation of the best scores of the cost function evaluations:

10

O b j_{1} (b) = \bar{f} (b) + λ \sqrt{\frac{1}{N - 1} \sum_{i = 1}^{N} {(f [α_{i}^{*}, τ_{i}^{*}] - \bar{f} (b))}^{2}},

where $N -$ 1 is the number of degrees of freedom in the vector of residuals, $\bar{f}$ is the sample mean of the cost function, $λ$ is a critical value corresponding to a given signiﬁcance level (e.g. three or six sigma rules may be easily applied), $α_{i}^{*}$ , $τ_{i}^{*}$ are optimal values of wavelet’s parameters at the $i$ th trial of the OAE algorithm. On the other hand, the time computational complexity of the main optimization algorithm is approximated using the total number of cost function evaluations as the product of the number of steps and the number of cost function evaluations at each step.

In the previous papers [11-13], the authors applied very complicated and parametrized measures for the formulation of the criterion corresponding to the accuracy of damage identification. In the current study, it is simplified by using the entropy-based measure in the following way:

11

f (α, τ) = E n t (W) = - \sum_{i, j} p (w_{i j}) l o g_{2} [p (w_{i j})],

where $W$ represents the matrix with values corresponding to detail coefficients obtained by means of the fractional wavelet decomposition (see more details in [12]), $p (∙)$ is the probability distribution function. A scalar value $E n t (∙)$ represents the entropy of magnitudes of elements in the matrix $W$ . In this case, the entropy is a statistical measure of randomness that can be used to characterize the texture of the detail coefficients.

Different multi-objective versions of soft computing methods often indicated in the literature can be used to solve the task of meta-optimization. However, the authors suggest applying a much less complicated algorithm in the main optimization engine (OAE), while more advanced approach in the meta-optimization core (MAC). Hence, it is possible to compute general values of relevant parameters of the main algorithm for which a priori knowledge is not necessary. The engine of the main optimization algorithm is prepared using the particle swarm optimization algorithm (PSO-OAE). The hard computing optimization methods (e.g. gradient-based approaches) could not be applied to this problem mainly because of the form of the criterion Eq. (11) and the measurement noise in the real-world data, which lead to the discontinuity of the multimodal objective function. Moreover, for these types of problems pure stochastic optimization methods such as random search, Monte Carlo techniques, etc. very often are not able to find an accurate solution with guaranteeing polynomial-time convergence. The selection of the PSO algorithm as the core of OAE was driven taking into account the comparison study on the performance of different soft computing methods for optimizing values of wavelet‘s parameters described by the authors in [12]. On the other hand, the core of the meta-optimization process is realized with the use of the multi-objective evolutionary algorithm (MOEA-MAC). The major argument for this can be seen in the form of multi-objective function Eq. (9). As one can observe, the problem is formulated as nonlinear multi-objective and mixed discrete-continuous problem. Furthermore, the most promising results presented by [16] as well as own research of the authors in this matter [13] were the basis for choosing multi-objective evolutionary computation method as the engine of MAC. MOEAs are based on the natural selection process that mimic biological evolution [17]. In this study, the genetic operators for multi-objective optimization proposed in [13] are employed to reach the convergence of a solution. In such a way, the problem is solved by computing the Pareto front and thanks to this the set of evenly distributed non-dominated optimal solutions are determined. PSO is a population-based stochastic optimization technique [18], which is inspired by simulation of a social behavior. In this paper, PSO is adopted and applied to search for the optimal values of $α_{i}^{*}$ , $τ_{i}^{*}$ . Both the optimization algorithms were implemented in the MATLAB^® environment using Genetic Algorithm and Particle Swarm Optimization Toolboxes.

3. Materials and experimental methodology

3.1. Tested structures

The developed damage identification procedure was applied to sandwich structures manufactured and supplied by PPHU Surfpol. The structures of spatial dimensions of 300×300 mm consist of a core of a thickness of 3 mm made of aramid paper saturated by phenolic resin with hexagonal cell configuration and face sheets made of glass-fiber reinforced laminate with a thickness of ca. 0.55 mm. The details on materials and manufacturing procedure can be found in [19]. Six cases of damaged sandwich structures were considered during experiments. They consist of partial (case Sand1) and full (case Sand2) local lacks of a core of irregular shape (in normal direction to the surfaces of the plates), through-the-width crack of a core (case Sand5), delamination on an interface between a core and a face sheet on the area of 360 mm² located in the geometrical center of a plate (case Sand6), and impact damage caused by various impactors – cases SandA25 and SandE10, where the letters denote a type of impactor (A for hemispherical R17 mm and E for conical with rounded tip of R5 mm). The schemes of the considered types of damage (cases Sand1, Sand2, Sand5 and Sand6) are presented in Fig. 1. The corresponding pictures of damaged structures can be found in [19].

Fig. 1Schemes of the considered types of damage

a) Sand1

b) Sand2

c) Sand5

d) Sand6

3.2. Modal analysis

The damaged sandwich structures were scanned using the laser Doppler vibrometer (LDV) Polytec^® PSV-400 in order to acquire modal shapes of natural vibrations on a net of 64×64 equidistant measurement points spanned on surfaces of the tested plates. The plates were clamped in a steel frame by 24 bolts around its perimeter, which resulted in reduction of scanning area to 250×250 mm. A reference signal was obtained by the point LDV Polytec^® PDV-100 focused on the clamping frame in order to exclude an influence of clamping frame. Before scanning, the tested structures were covered by Helling® anti-glare spray in order to improve focusing of laser beam of scanning LDV. The frame with a mounted plate was excited using electrodynamic shaker TIRA^® TV-51120 by pseudo-random noise signal generated from LDV-dedicated software and amplified by the power amplifier TIRA^® BAA 500.

The frequency bandwidth during the modal analysis was set in the range of 0-2 kHz with a frequency resolution of 1.25 Hz. The frequency response function (FRF) obtained during measurements for each measured point was averaged ﬁve times. From the obtained FRFs from a whole set of measurement points in a particular experiment the modal shapes of vibrations were selected as follows: if the magnitude of vibrations of a given modal shape is higher than 20 % of a maximal magnitude of vibrations observed in FRF for a tested structure, then it is considered during further analysis. This procedure allows excluding the modal shapes with a low amount of diagnostic information and a high noise level. Results of selection of modal shapes for investigated cases with corresponding natural frequencies of vibration can be found in [19].

4. Results of damage identification

The cost function in the PSO-OAE was computed using Eq. (10). In this algorithm only few parameters are relevant to guarantee, as far as possible, to find the optimal solution of the problem. Therefore, behavioral parameters such as the social and cognitive attraction coefficients, the number of particles, and the total number of generations only were taken into account during the meta-optimization process realized by means of MOEA-MAC.

The lower and upper boundaries of the PSO-OAE were assumed corresponding to wavelet’s properties, in particular $0 \leq α \leq 3$ and $0 \leq τ \leq 1$ , whereas in the case of MOEA-MAC the boundaries were declared in such a way that the number of particles and the total number of generations were equal from 5 to 35, the cognitive and social attraction were set from 0 to 4. The guidelines given in the literature were employed to obtain the best results from the MOEA. The fitness function was declared following to Eq. (9), where $O b j_{1}$ was computed by averaging the best fitness function for $N =$ 25 and $λ =$ 3 and $O b j_{2}$ was obtained as the product of the number of particles and the total number of generations of the OAE. Individuals in the population of the MOEA composed of genes representing real numeric values of behavioral parameters. The total number of generations of MOEA was set to 30. The population size of this algorithm was equal 40. The fraction parameter was equal to 0.8. The user-defined parameter for a heuristic crossover operator was set to a default value, and the crossover probability was equal 0.8.

The optimization results obtained by the authors in this case study are summarized in Table 1. It can be seen that computed values of relevant parameters of the main optimization algorithm are quite different for each specimen. This is caused by the complex, non-linear and non-smooth nature of the objective function Eq. (10).

Table 1Overall results of the meta-optimization process and their influence on the results of optimization of wavelet’s parameters

MOEA-MAC/ PSO-OAE							PSO
Specimen ID	Cognitive attraction	Social attraction	Gen.	Pop. size	$O b j_{1}$	$O b j_{2}$	$E n t$	$α$	$τ$
Sand1	0.94	1.02	16	20	6.89	320	4.44	0.3631	0.0031
Sand2	0.50	1.24	15	6	4.79	90	3.04	1.0494	0.0274
Sand5	0.54	1.18	31	13	9.20	403	5.92	0.9678	0.9966
Sand6	1.35	1.51	27	7	5.29	189	3.40	1.7155	0.8846
SandA25	0.35	0.94	21	9	8.96	189	5.76	0.8065	0.0941
SandE10	0.36	1.01	34	13	8.88	442	5.72	1.4007	0.4070

A much more important conclusion can be stated taking into account the second objective. As one can see in Table 1, the time complexity of the main optimization algorithm is in the range from 90 to 442 cost function evaluations and this strongly depends on the form of a damage. To better understand these investigations optimization results for two specimens (Sand1, SandE10) are presented precisely in Figs. 2 and 3. The two plots in Fig. 2 illustrate the compromise solutions obtained in the multi-objective meta-optimization process. The best solution was selected from non-dominated optimal solutions that were characterized by the accuracy of the cost function as higher as possible (in a statistic sense) with the acceptable time complexity of the algorithm, which means that the solution was selected exactly from the center of Pareto front. Moreover, in Fig. 3 the convergence plots of PSO are given for the best values of behavioral parameters confirming the high capability of the proposed rule.

Several exemplary results obtained for the best values of wavelet’s parameters computed by means of the meta-optimization method are presented in Fig. 4 in order to illustrate the high detectability and traceability features of the proposed approach.

One can notice that the values of $α$ and $τ$ obtained from the above-described meta-optimization procedure (see Table 1) are in general low. Obtaining of such solutions can be explained by a fact that the increase of $α$ is connected with an increase of the number of vanishing moments, which positively influences on stability of the wavelet-based algorithm and detectability performance. However, the increase of $α$ is also connected with occurrence of distortion around the identified singularity (damage), which increases the overall entropy of the resulting pattern. According to the formulated criterion of minimization of Eq. (11) the entropy is minimized. Thus, the obtained optimal solutions are reached in such a way that the entropy is minimized and the wavelet order is high enough to identify the singularities with a minimal distortion.

Fig. 2Examples of the compromise solutions obtained in the multi-objective meta-optimization process

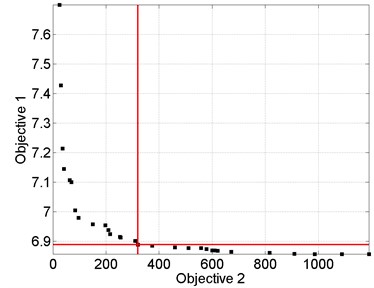
a) Sand1

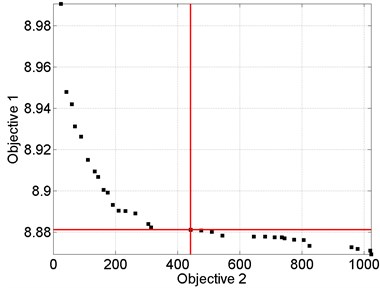
b) SandE10

Fig. 3Selected results of the particle swarm optimization performed for the best values of behavioral parameters

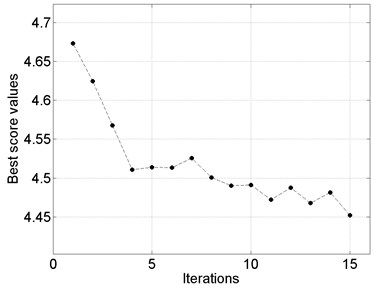
a) Sand1

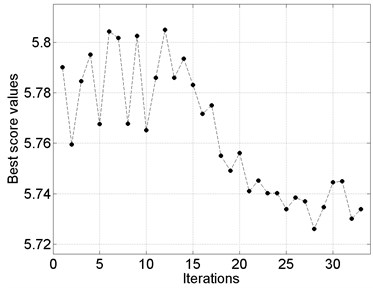
b) SandE10

In several cases (see Fig. 4(c), (e), (f)) the characteristic rings are observable, which were wrongly identified as damage. The same artifacts were also observed in the previous studies on damage identification in sandwich composites [19]. These artifacts resulted from the improper ﬁltering of particular modal shapes during the wavelet analysis. The main reason of this phenomenon is too low number of measurement points, which causes a discontinuity in the region, where the magnitudes of the ﬁrst modal shapes started to increase. Nevertheless, the increase of number of measurement points increases also the overall time of measurements and computations.

In order to evaluate the effectiveness of the proposed procedure the extent of true damage (obtained from the measurements on the considered structures) and resulting sets of coefficients presented in Fig. 4 for the cases with spatial damage (Sand1, Sand2 and Sand6) were compared. For the comparison the area of damage in mentioned cases was selected. For the resulting set of coefficients the following rule for the determination of extent of identified damage was applied: if a value of a given coefficient is higher than 20 % of maximal value of coefficients in a considered set, then it is considered in the determination of damage extent. The obtained results are presented in Table 2.

Table 2Comparison of damage extent for the cases with spatial damage

Case	True extent, mm²	Identified extent, mm²	Error, %
Sand1	336.36	312.5	7.09
Sand2	99.67	117.19	–17.58
Sand6	360	113.28	68.53

Fig. 4Results of damage identification in sandwich structures based on optimal values of wavelet’s parameters

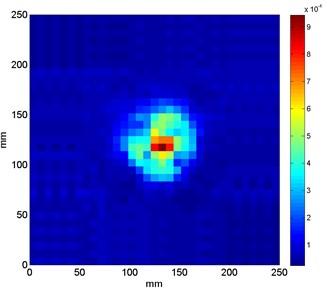
a) Sand1

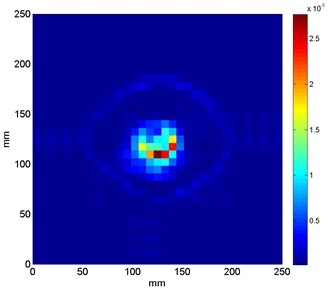
b) Sand2

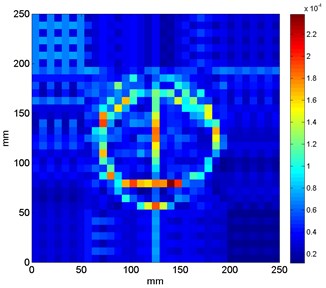
c) Sand5

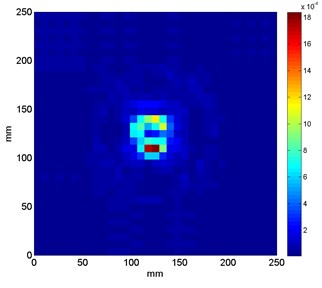
d) Sand6

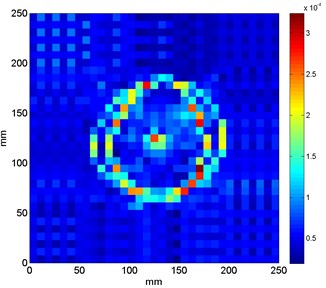
e) SandA25

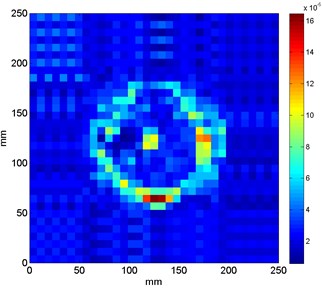
f) SandE10

One can notice that in the cases with partial (Sand1) and full (Sand2) local lack of a core the extent of damage is determined accurately using the proposed approach. For the case of delamination on an interface between a core and a face sheet the identified extent is much lower than the true extent of delamination. This can be explained by a low amount of change in magnitudes at the boundaries of delaminated area as well as the assumed threshold during determination of damage extent from the sets of resulting coefficients. Considering the obtained results the proposed method is not always effective in determination of damage extent. It is also justified by small spatial resolution of analyzed modal shapes as well as mechanical specificity of an analyzed damage.

5. Conclusions

In the following study the hybrid wavelet-based algorithm with multi-objective meta-optimization of selection of wavelet’s parameters was proposed. The main advantage of the proposed algorithm is that the a priori knowledge on wavelet and optimization parameters is not necessary, which allows automating the damage identification algorithm. Moreover, the applied entropy-based criterion is characterized by simplicity of computation and better effectiveness in comparison with the previously developed criteria [11-13]. The proposed algorithm was tested on experimental modal curvatures of sandwich composite structures with various types of internal and external damage. Obtained results show that the optimally selected parameters are in agree with expectations and theoretical fundamentals of FrWT.

References

Chang C. C., Chen L. W. Damage detection of a rectangular plate by spatial wavelet approach. Applied Acoustics, Vol. 65, 2004, p. 819-832.

Search CrossRef
Bagheri A., Ghodrati Amiri G., Seyed Razzaghi S. A. Vibration-based damage identification of plate structures via curvelet transform. Journal of Sound and Vibration, Vol. 327, 2009, p. 593-603.

Search CrossRef
Fan W., Qiao P. A 2-D continuous wavelet transform of mode shape data for damage detection in plate structures. International Journal of Solids and Structures, Vol. 46, 2009, p. 4379-4395.

Search CrossRef
Xu W., Cao M. S., Radzieński M., Xia N., Su Z., Ostachowicz W., Wang S. S. Detecting multiple small-sized damage in beam-type structures by Teager energy of modal curvature shape. Journal of Vibroengineering, Vol. 17, 2015, p. 275-286.

Search CrossRef
Rucka M., Wilde K. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. Journal of Sound and Vibration, Vol. 297, 2006, p. 536-550.

Search CrossRef
Katunin A., Holewik F. Crack identification in composite elements with non-linear geometry using spatial wavelet transform. Archives of Civil and Mechanical Engineering, Vol. 13, 2013, p. 287-296.

Search CrossRef
Yam L. H., Yan Y. J., Jiang J. S. Vibration-based damage detection for composite structures using wavelet transform and neural network identification. Composite Structures, Vol. 60, 2003, p. 403-412.

Search CrossRef
Rucka M., Wilde K. Neuro-wavelet damage detection technique in beam, plate and shell structures with experimental validation. Journal of Theoretical and Applied Mechanics, Vol. 48, 2010, p. 579-604.

Search CrossRef
Hein H., Feklistova J. Computationally efficient delamination detection in composite beams using Haar wavelets. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 2257-2270.

Search CrossRef
Xiang J., Liang M. A two-step approach to multi-damage detection for plate structures. Engineering Fracture Mechanics, Vol. 91, 2012, p. 73-86.

Search CrossRef
Katunin A., Przystałka P. Detection and localization of delaminations in composite beams using fractional B-spline wavelets with optimized parameters. Eksploatacja i Niezawodnosc – Maintenance and Reliability, Vol. 15, 2014, p. 391-399.

Search CrossRef
Katunin A., Przystałka P. Damage assessment in composite plates using fractional wavelet transform of modal shapes with optimized selection of spatial wavelets. Engineering Applications of Artificial Intelligence, Vol. 30, 2014, p. 73-85.

Search CrossRef
Katunin A., Przystałka P. Meta-optimization method for wavelet-based damage identification in composite structures. Proceedings of the Federated Conference on Computer Science and Information Systems, Warsaw, 2014, p. 435-444.

Search CrossRef
Unser M., Blu T. Fractional splines and wavelets. SIAM Reviews, Vol. 42, 2000, p. 43-67.

Search CrossRef
Chaudhury K. N., Unser M. Construction of Hilbert transform pairs of wavelet bases and Gabor-like transforms. IEEE Transactions on Signal Processing, Vol. 57, 2009, p. 3411-3425.

Search CrossRef
Smit S. K., Eiben A. E. Comparing Parameter Tuning Methods for Evolutionary Algorithms. Proceedings of IEEE Congress on Evolutionary Computation, 2009, p. 399-406.

Search CrossRef
Deb K. Multi-Objective Optimization Using Evolutionary Algorithms. Wiley, 2009.

Search CrossRef
Mikki S. M., Kishk A. A. Particle Swarm Optimization: A Physics-Based Approach. Morgan and Claypool, 2008.

Search CrossRef
Katunin A. Vibration-based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis. Composite Structures, Vol. 118, 2014, p. 385-391.

Search CrossRef

About this article

Received

02 April 2015

Accepted

05 July 2015

Published

30 September 2015

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

vibration-based damage identification

fractional wavelet transform

multi-objective meta-optimization

composite structures

Acknowledgements

The research project was financed by the National Science Centre (Poland) granted according the decision no. DEC-2011/03/N/ST8/06205.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.