Integration on acceleration signals by adjusting with envelopes

1. Introduction

Signals are important to fault diagnosis of machines. Accelerometers are the most widely used transducers to measure vibration because of its ability to pick up high frequency content and higher sensitivity. In some practical application, it is advisable to obtain position from integrating the acceleration instead of using position sensors because displacements are difficult to measure in some special cases. Using accelerometers to obtain position has the advantages such as avoiding tight tolerances for alignment in sensor installation, reducing cost, and causing minimal interference to original system dynamics [1]. It is known that we can get displacement signals from acceleration signals by using double integration. However, direct integration on acceleration signals will cause unrealistic drifts in velocity and displacement signals.

In order to remove the drifts in velocities and displacements, it is necessary to obtain the baseline offsets. Several methods are proposed to estimate the baseline offsets. Gilbert et al. [1] have designed integrator circuits by using analog filter for long-term real-time integration of acceleration to measure position. Yang et al. [2] has proposed a method that the acceleration data is firstly baseline-corrected in the time domain using the least-square curve fitting technique, and then processed in the frequency domain using a windowed filter to further remove the components caused oscillations in displacement. In addition, the multi-rate Kalman filtering method [3] and the spectral subtraction method [4] are also used to estimation displacement through integration on acceleration.

Envelopes of signals can be used to estimate the baseline offsets. It is well known that envelope contains some information of signals though it is an imaginary curve. It can be used to demodulate conventional amplitude modulated (AM) signals. Envelopes is used by Huang et al. [5] to bring an adaptive signal processing method, empirical mode decomposition (EMD). In the EMD algorithm, the upper and lower envelopes of signals are formed by using two steps [5]: 1) identify all the local extrema, and 2) interpolate between maxima (resp., minima) by a cubic spline. Our previous work [6] has shown that the process of forming the upper and lower envelopes of signals involves three steps: 1) extrema sampling, 2) interpolation, and 3) filtering by a cubic B-spline filter by analyzing a cubic B-spline interpolation. Furthermore, envelope of signals is regarded as the signal reconstructed from the extrema sequence from the digital signal processing point of view [7, 8]. In fact, envelope represents the lower frequency components of signals. Inspired by envelopes used in the EMD method and these new recognitions on envelopes, we want to provide a method of digital integration on acceleration signals by using envelopes.

2. Drifts of direct integration

The reasons for drifts in velocities and displacements derived by integrating acceleration signals can be described as offset in accelerations, random noise in accelerations, and so on [2]. It is common sense that displacement is the integral of velocity, which in turn is the integral of acceleration. For a measured acceleration $a\left(t\right)$, the velocity can be written as:

where $v_0$ denotes the initial velocity. The displacement which is the integral value of $v\left(t\right)$ is expressed as:

where $s_0$ represents the initial displacement. Eq. (2) shows that the initial velocity and the initial displacement must be known to estimate the displacement for a double integration to be performed on acceleration. If the initial velocity and the initial displacement are zero, then the displacement can be required by using Eq. (2). However, they are not zero in most of case, which will bring an integration error to the displacement.

Numerical integration is widely used in engineering. There are a number of discrete integration algorithms, such as the rectangular integration method, the trapezoidal method, and the Simpson’s method. The acceleration signal is first sampled, and then integration is performed. Even small errors in the measured acceleration will produce larger drifts in the velocity and displacement. Thong et al. [9] have developed a root mean square positional error estimates for numerical double integration with the trapezoidal and rectangular method.

In addition, noise is another reason of causing drift. The presence of noise during dynamic measurements is regarded as one of the main sources of errors during integration procedures [4].

After integration, low frequencies components are strongly amplified and high frequencies components are reduced. Time integration amplifies the low frequency components of the signal and any measurement error is significantly amplified [10]. In fact, the drift is just represented by the constant and some very slowly changing components.

3. Drifts adjusting by envelopes

The algorithm uses double integration to derive a position signal from an acceleration signal through adjusting shift by envelopes. A block diagram of the double integration process is shown in Fig. 1. First, an acceleration signal is integrated by using a numerical integration method such as the Simpson’s method. Usually, the integrated signal is dominated by some drifts. Then, the upper and lower envelopes of the integrated signal are calculated. The mean of the upper and lower envelopes is further calculated to obtain the baseline offsets. Finally, a velocity signal is obtained by reducing the mean of the upper and lower envelopes from the integrated signal. This is the first integration on acceleration. To derive a position signal, second integration on velocity is performed. Similarly, repeat above steps on the velocity can find the displacement signal.

For a given discrete signal $x\left(n\right)$, the process of shift adjusting by envelope can be shown as follows.

1) Identify all the local extrema of $x\left(n\right)$.

2) Interpolate between maxima (resp., minima) by a cubic spline to form the upper envelope $e_u\left(n\right)$ (resp., the lower envelope $e_d\left(n\right)$).

3) Calculate the mean of the envelopes $e_a\left(n\right)=\left(e_u\right(n)+e_d(n\left)\right)/2$.

4) Compute $y\left(n\right)=x\left(n\right)-e_a\left(n\right)$.

Envelope represents the lower frequency components of signals. However, only the upper envelope or the lower envelope cannot be used to remove the shifts. It is shown in [8] that the upper and lower envelopes contain two parts, some components of the original signal and some new components generated by the sub-Nyquist extrema sampling. Fortunately, the mean of the envelopes can weaken even eliminate the aliasing noise [6]. This is just the reason that the mean of upper and lower envelope of signals are used to remove the shifts. Some examples to evaluate the performance of the proposed algorithm are presented in next section.

Fig. 1Block diagram of double integration process

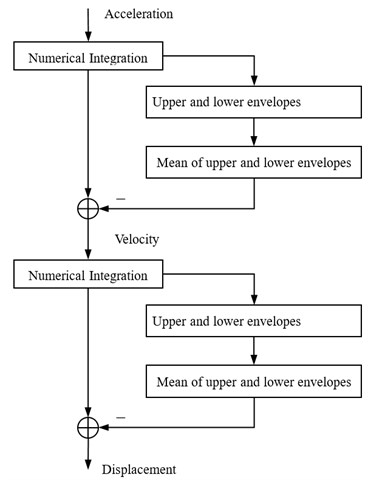
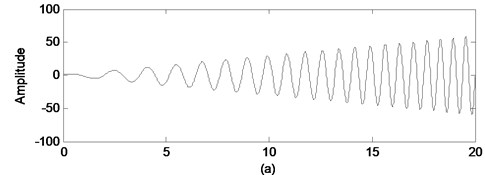
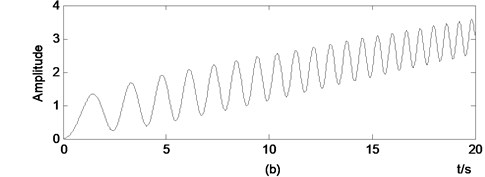
Fig. 2Acceleration used in example I: a) acceleration, b) displacement obtained by double integration

4. Numerical examples

4.1. Example I

Shown in Fig. 2(a) is an acceleration time series with the characteristic of frequency changes with time. The displacement derived by doubly integrating on acceleration is presented in Fig. 2(b). It is clear shown in Fig. 2(b) that the displacement has an unreasonable drift.

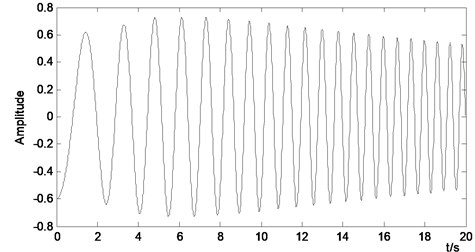
By using envelope to adjust the drift, the corrected displacement is illustrated in Fig. 3. It can be seen that the displacement waveform is symmetric about the zero line. Comparing Fig. 3 with Fig. 2(b), it is obvious that the drift generated by the direct integration is removed by the envelope method.

Fig. 3Displacement corrected by the envelope method

4.2. Example II

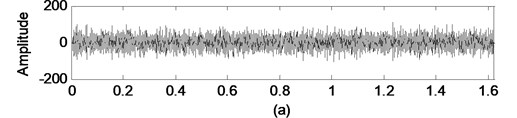
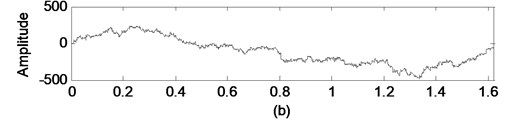
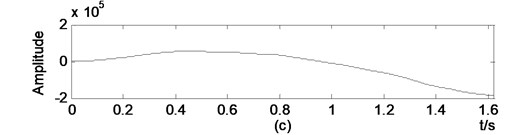
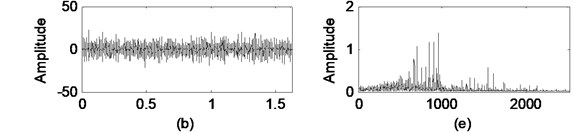
The direct integration results of a real world data collected from a compressor are shown in Fig. 4. Fig. 4(a) shows that the real world data has many components. Fig. 4(b) and Fig. 4(c) show that the velocity and displacement obtained by direct integration from acceleration are dominated by a serious drift.

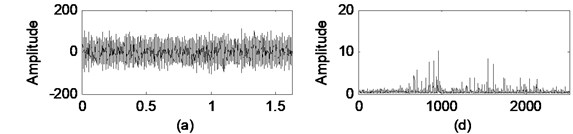
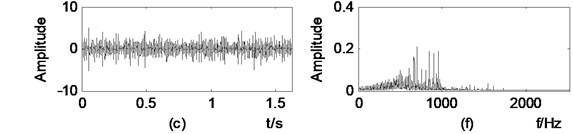
Fig. 5 presents the corrected velocity and displacement by using the envelope method. It is obvious that the velocity and displacement waveform are symmetric about the zero line. Comparing Fig. 5 with Fig. 4, we can see that the drifs generated by the direct integration in velocity and displacement are removed by the envelope method. We can conclude that the proposed algorithm can yield a reasonable displacement.

Fig. 4Illustration drifts generated by direct integration on a real world data: a) acceleration, b) vibration obtained by integration, c) displacement obtained by double integration

5. Conclusion

In the present paper, we have investigated the technology of numerical integration of acceleration to estimate position. We have proposed a simple algorithm for digital integration of acceleration to acquire velocity and displacement by using envelopes. The drift generated by direct integration of acceleration is estimated by the mean of the upper and lower envelopes of signals. The numerical examples are presented to demonstrate the effective and feasibility of the algorithm.

Fig. 5Illustration the corrected vibration and displacement shown in Fig. 4: a) acceleration, b) vibration, c) displacement, e) to f) are the spectrum of the left corresponding panel