Numerical models of railway tracks for obtaining frequency response Comparison with analytical results and experimental measurements

1. Introduction

One of the main problems to be considered when planning a new railway line is the impact of noise and vibrations on the surrounding areas. This influence is particularly noticeable in urban railway lines, where the principal disadvantage on the surface is air-borne noise emission, while in the subway it is ground-borne vibrations that cause more trouble to residents living near the lines [1].

The vibration transmission into buildings surrounding the railway lines produces disturbance associated with the direct perception of the vibrations and also with the noise induced. The main cause of the vibrations generated by railway traffic is the irregularities of the wheel and rail profiles. These irregularities generate fluctuations of the wheel-rail contact force, which are responsible for the generation and transmission of vibrations to the environment as well as for fatigue damage and wear of the rolling stock. The vibration generation depends on the vibratory responses of the railway track and the assembly consisting of the wheelset and the primary suspension. Moreover, the vibration levels will be intensified with an increase in the train’s speed, the loads on each axle and, principally, with the worsening of wheel and rail profiles.

In order to dispose of methodologies for measurement and control of vibrations produced by the passage of a train, the Mechanical Engineering Department (DEM) of the Universitat Politècnica de Catalunya, in Spain, is carrying out a research program with a double goal: the development of monitoring techniques for the control of the train wheels condition, mainly for the case of metropolitan railways, and the design of simulation tools, based on the wheel-rail contact force mechanism, for assessing the vibration levels present in the railway track superstructure. These simulation tools will provide support for the development of the monitoring techniques and moreover can be used as a constituent part of global models for the vibration generation and transmission to the railway track surroundings. The global models are of special interest for the prediction of vibration levels during the planning of new railway lines. As an example of the usefulness of the generation models, researchers from DEM have carried out simulations using this kind of models in order to assess and compare the capability of attenuating vibrations for different types of railway tracks, and so obtain alternative solutions to be applied in troublesome track sections of the Metropolitan Railway of Barcelona (FCMB) [2].

Many authors have dedicated their studies to characterizing the vibrations produced in different types of railway tracks under moving loads, and have developed various theories and analytical models [2-5]. These models are generally composed of an infinite straight half-track in contact with a railway wheel suspended from its primary suspension. Two fundamental models can be found in bibliography [6-8]: the first one is known as the continuous model and considers that parameters of all track elements are modeled as continuous longitudinal layers under the rail. These parameters are the stiffness and damping of fasteners and ballast and the inertia of sleepers or blocks, depending on the track type. In the second model, the discrete model, the railway track elements are treated as individual elements, with their own inertia, stiffness and damping, which allow modeling the effect of distance between fastenings or sleepers on the track’s behavior. In both analytical models, the infinite Euler beam or the infinite Timoshenko beam can be used to model the rail.

Although the analytical half-track models have been widely used, they present the disadvantage of not considering factors that affect the mechanism of vibration generation, such as the bending stiffness of the sleepers, the distributed ballast stiffness, or the transmission of vibrations between both rails through the track superstructure.

This article presents complete railway track models, numerical models that can study the interaction between rails; these models are established using the finite element method (FEM), and are designed to characterize the mechanism of vibration generation. The models are able to define the frequency response of the tracks and evaluate the numerical data in comparison with the described analytical results [9, 10]. Finally, two real cases are studied and a comparison is made between the numerical and experimental results.

The authors have also developed a numerical model of wheelset systems [11]. This model, combined with the numerical models of the railway tracks presented in this paper, leads to the definition of wider models that describe the mechanism of vibration generation due to wheel-rail contact. These models, that will allow the analysis on the vibration transmission not only via the track superstructure but via the wheelset, will be presented in a future publication.

2. Track numerical models

The FEM needs to introduce all the fundamental parameters -the material properties and geometric parameters- in order to solve the problem. The parameter data used for processing is made up, first of all, by the rail properties (elastic constants, damping factors, materials, etc.), and afterwards by the real geometric parameters, such as the distance between rails, the separation between sleepers and the length of the rail track.

Fig. 1Half-track numerical models

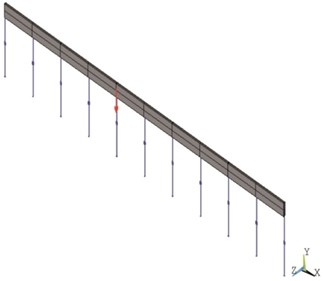
a) DFF track

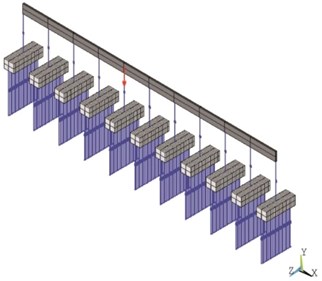
b) Bi-block slab track

In order to develop numerical models, the general purpose finite element analysis package, ANSYS 13 was used [12, 13]. The aim is to identify the vibration response of a straight railway track when vertical forces are applied to the top of the rails. In the present paper, four numerical track models are presented. The first two models correspond to straight single half-tracks, with only one rail in longitudinal direction. These models assume that there is no interaction between rails throughout the infrastructure. The first represents a Direct Fixation Fastener (DFF) half-track (Fig. 1(a)) and the second a bi-block slab half-track (Fig. 1(b)).

The last two models describe complete tracks. A STEDEF type track is modeled in the third numerical model and the fourth one refers to a ballasted track with concrete mono-block sleepers (classical track). Both models consider some characteristics of the track dynamic behavior that are not included in the first two models, for example the interaction between rails. Figs. 2(a) and 2(b) respectively show the software design of the STEDEF track and classical track.

The components of the different models are described with the use of several ANSYS library elements [14]. When selecting the type and size of the elements to use, it should be taken into account that the frequency range to be considered runs from 10 up to 400 Hz. This range includes the characteristic frequency band of vibrations produced by wheel-rail contact [6].

Fig. 2Complete numerical models

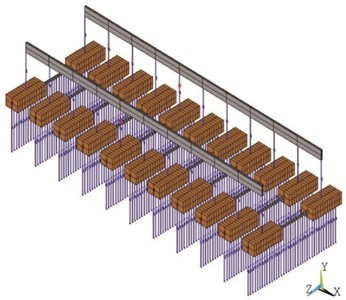
a) STEDEF track

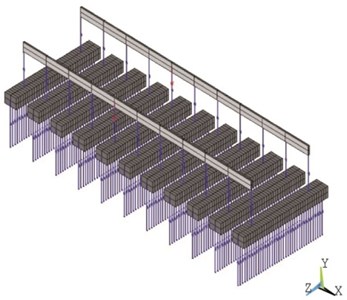
b) Classical ballasted track

The definition of the elements used in the modeling is as follows:

The rail is modeled as the union of Timoshenko-beam elements, where every beam length corresponds to the distance between sleepers. In this way the end nodes are used to link them to the rail fastenings (track fasteners). The beam element is particularly suitable because it allows the introduction of the real parameters of the rail: density, elastic modulus and Poisson’s ratio, structural damping and, finally, the geometric parameters: area and second order momentum of the section.

The rail fastenings are treated as linear elastic-spring elements with hysteresis damping that connect the rail to the sleepers.

The sleepers are represented in two different ways, depending on the track model: In both half-track models, the sleepers are treated as point masses equal in value to the mass of half sleeper. In the last two track models, the sleepers are modeled, as in the case of the rail, using Timoshenko beam elements. The chosen number of elements is 70, because it allows the link of each sleeper with the distributed ballast or the slab material under it, to be modeled sufficiently precisely.

Finally, the ballast of the classical track and the rubber pads located under the blocks, present in the case of bi-block and STEDEF type track, are modeled by means of a distribution of linear elastic spring elements with hysteresis damping connected on one side to the sleeper or block nodes and on the other side to the rigid base of the track.

Another fundamental key aspect of the models description is the definition of the boundary conditions upon which the dynamic behavior of the modeling system depends directly:

The infrastructure supporting the track is assumed to be rigid. Although this is not a real condition, since the vibration is transmitted to the environment, it has been verified that the stiffness of the base, higher than the overall track stiffness, has little influence on the vibration generation mechanism caused by the rolling [2, 5].

It is known that on a straight stretch of track, the vertical vibration is the most significant and the force of wheel-rail contact is essentially vertical. Therefore, only vertical exciting forces are considered and the degrees of freedom of the nodes in the models are all restricted to allow only the vertical movement of the track elements, as well as the transverse bending of the beam elements.

A minimum track length of 60 m, combined with the system damping, is enough for the simulation of the end boundary conditions of an infinitely long straight real track when a force is applied to the top of the rail located just in the mid-section of the track model.

All the elements used in the models have linear behavior. In the case of elements that represent the elastomeric stiffness, a dynamic rigidity is considered. Regarding ballast, a stiffness representative value of consolidated ballast after a long period of service is used [9, 10]. The dynamic analysis in the numerical assessment of the railway track behavior is adopted. This analysis provides temporal variation of displacements, stresses, strains and forces when a model structure is submitted to a combination of loads that vary over time. To obtain this kind of solution, the effects of inertia and damping are essential. In the presented numerical models, harmonic loads with variable frequency are considered in order to determine the frequency response of the track.

The general equation to be solved in a dynamic analysis is as follows:

where $\mathbf{M}$ is the matrix of inertia, $\mathbf{C}$ is the viscous damping matrix, $\mathbf{K}$ is the stiffness matrix, $\ddot{\mathbf{u}}$, $\dot{\mathbf{u}}$, $\mathbf{u}$ are respectively the vectors of acceleration, velocity and displacement related to nodal coordinates, and finally $\mathbf{F}$ is the external force vector depending on time. In the case of structural or hysteresis damping, and always for harmonic solutions of the equation system, the viscous damping matrix disappears and a stiffness matrix of complex components is introduced. This is the approach considered in the present work, with the structural damping introduced as a loss factor.

In ANSYS 13, three different analysis methods are available for solving the set of equations representing the system. In this analysis, the authors have opted for the full method. This method considers all degrees of freedom of the system and solves the general dynamic equation at any time. It's the easiest of the three methods but also the most time-consuming; however, this is not a serious problem as the number of nodes is not very high. The results of the integration process are expressed as frequency responses.

The numerical results of the different track types are compared below with analytical model results, developed in the literature [2-5].

3. Comparison of numerical and analytical models

In order to ascertain the validity of the track numerical models, the track frequency responses from numerical models have been contrasted with responses provided by the continuous analytical model. The comparison is made in the frequency domain by means of the rail vertical receptance, which expresses the vertical displacement of the rail, $y_c$, in a certain location as a function of the harmonic vertical force, $F$, applied at the same -or different- location, for all frequency $f$ in the range of interest.

The receptance equation is:

where $\phi$ is the phase between the displacement $y_c$ and the applied force $F$. The analytical models of the half tracks, both the continuous and the discrete, have been developed in previous works and presented in several publications [2, 7, 8]. In both cases the rail can be treated as an Euler-Bernoulli infinite beam or a Timoshenko infinite beam; both provide practically the same results in the frequency range of interest. The two models also provide equivalent results if train speeds are under 100 km/h [8]. This condition is fulfilled in the case of metropolitan railways, which is the case analyzed in the present study. Fig. 3 shows a scheme of the half-track distributed parameter analytical model used in the comparative.

Fig. 3Classical ballasted half-track model, side view

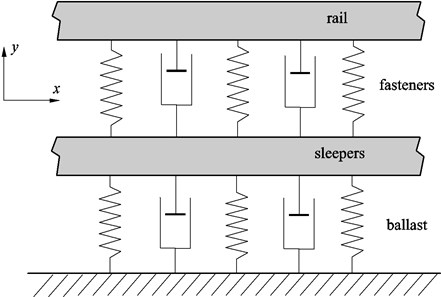
The comparison is made for the classical ballasted track and for the three slab tracks considered: DFF half-track, bi-block half-track and the STEDEF track. The harmonic exciting force is applied to the rail, directly above a sleeper or a fastener.

The parameters used in this first comparison are set out in Table 1; these parameters are from information provided by the Metropolitan Railway Company of Barcelona, in Spain, (FCMB) and from the literature. The parameters of the analytical model can be deduced from those presented in Table 1, transforming them into distributed parameters: magnitude per unit of length of the track $x$-coordinate.

Comparison of receptance magnitudes obtained with both numerical and analytical models is shown in Fig. 4(a) for the DFF half-track. The receptance corresponds at the point of the vertical excitation force. It is noted that the differences are not significant for the frequency range between 0 and 600 Hz, which comprises the frequency range of interest mentioned above. The observed natural frequency is related to the normal mode of vertical vibration of the rail fixed on the elastic fasteners.

Fig. 4(b) presents the same comparison made in Fig. 4(a), but for the case of a slab track with bi-block sleepers, also using a half-track model; again, the two receptance, numerical and analytical, are virtually identical in all the frequency range. In this comparison, two normal modes of the track can be detected at 58 and 351 Hz. In the first one the rail and the blocks tend to vibrate in phase, while in the second one they tend to vibrate in counter-phase. The properties of this last mode depend not only on the stiffness under the blocks but also on the characteristics of the elastic fasteners located between the concrete blocks and the rail.

The good concordance between the numerical and analytical frequency responses shown in Fig. 4(a) and Fig. 4(b) for half-tracks can be considered a validation of the numerical models presented.

Fig. 4Numerical and analytical receptances

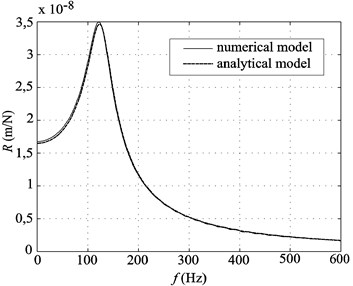
a) DFF half track

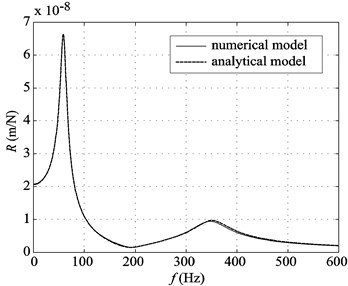
b) Bi-block half track

The receptance comparison of a STEDEF track can be seen in Fig. 5(a); it should be pointed out that in this instance a complete numerical model is adopted. To maintain the symmetry of the vertical movement of the railway track, an identical harmonic force must be employed to excite the two rails at points situated on the same sleeper. In this way, the comparison is made with an analytical model of a single half-track, which involves the symmetrical vertical movement of the two rails. The first normal mode is at the same frequency, 58 Hz, but the amplitude of the receptance is not exactly the same. In the second normal mode of vibration, the numerical natural frequency is slightly lower than the analytical one.

Fig. 5(b) corresponds to the comparison between the receptance of classical ballasted track, obtained using the complete numerical model, and the analytical receptance from the half-track analytical model. In this comparison, the same approach used in the previous comparison is applied to maintain symmetric movement of the track in the vertical direction. The differences between numerical and analytical results are comparable to those found in the case of a STEDEF track.

These differences are due to the effect of the bending stiffness of the sleepers, not taken into account in the analytical models or in the numerical models that consider only a single half-track, in which the sleepers are modeled as point masses. It should be mentioned that the mass distribution in the numerical models is more realistic than that used in the analytical models.

One of the main advantages of the full numerical models over the analytical half-track models is that the former include the dynamic interaction between both rails of the track through the sleepers and the ballast. Fig. 6(a) and Fig. 6(b) show the receptances of the two rails in the case of an exciting harmonic force employed only on one rail, rail 1, with rail 2 being the other. The considered point on both rails is located over the same sleeper. The contrast of the displacements in both rails along the frequency range is obvious. The mitigation of the vibration produced by the vertical exciting force is considerable, so it is concluded that the interaction between rails for the two types of track considered is small.

Fig. 5Numerical and analytical receptances

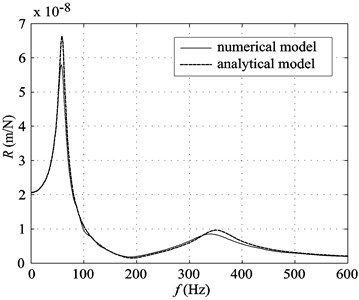
a) STEDEF track

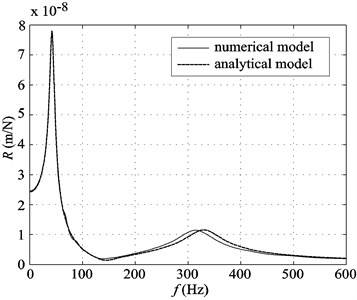
b) Classical ballasted track

Fig. 6Receptances determined with the numerical model at the rail 1, where the force is applied, and at the opposite rail 2

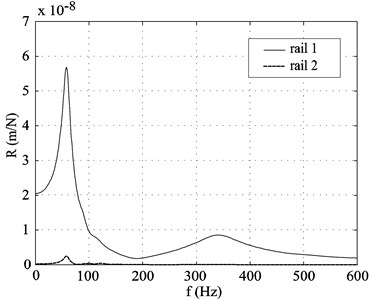
a) STEDEF track

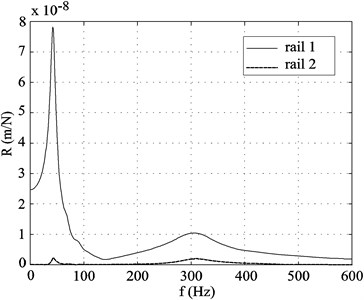
b) Classical ballasted track

4. Experimental results

In order to validate the full numerical models, a comparison is made between the numerical and experimental results for two types of tracks. The first is a traditional ballasted track with wooden sleepers, and the second is a STEDEF type track (Fig. 7(a)). The results are expressed in terms of frequency responses of the tracks. The two railway tracks available are straight sections from lines in service belonging to the Metropolitan Railway of Barcelona (FCMB). To excite vibration on both tracks, an electrodynamic shaker has been used, attached to the head of the rail by means of a fastening plate with clamps (Fig. 7(b)).

The shaker has been placed above a sleeper. The amplifier that powers the shaker is controlled by a sinusoidal signal generator with adjustable frequency. A mass of 2 kg is fastened to the mobile base of the shaker so that, when vibrating, it generates the harmonic exciting force that is transmitted to the rail through the fastening plate.

Using accelerometers placed on this mass and in various locations of the track, which include both rails, the vibration signals for frequencies between 20 and 400 Hz have been recorded. In order to register the vibration signals, a multi-channel data acquisition system has been used, which digitizes all the signals simultaneously and stores them in the computer hard disk. Finally, the information has been treated with applications developed using MATLAB [15]. These applications have been used for the assessment of the receptance at the point of excitation and the cross receptances between the point of excitation and any other accelerometer location on the railway track. The magnitude of the exciting force has been determined from the signals provided by two accelerometers, the first fixed to the vibrating mass and the second to the rail next to the actuator.

Fig. 7a) Straight section of a STEDEF track from FCMB, b) disposition of the electrodynamic actuator attached to the rail head above a sleeper

a)

b)

5. Validation of the numerical model

Once the experimental phase is complete, the results obtained during the tests are analyzed and compared with those obtained by numerical modeling using the finite element program.

Table 2 shows the parameter values of the tested tracks used in the numerical models. These values were obtained from direct measurements on the test tracks. The rail parameters, the rail gauge and the steel and concrete properties are those presented previously in Table 1.

The comparison between the experimental results and the results provided by the numerical models is made in the frequency domain using the vertical rail receptance. For the numerical models, the harmonic exciting force is applied to the head of the rail, just at the point where the sleeper or a fastener is located, thereby reproducing the test conditions. The available stretches of track used to perform each of the experimental measurements are straight and long enough to approximate the conditions of an infinitely long railway track.

Figs. 8(a) and 8(b) show the comparison between receptances obtained experimentally and those calculated numerically for the tested tracks, both at the point where the exciting force was applied. For the numerical calculations, a frequency resolution of 10 Hz from 20 to 400 Hz has been used according to the experimental results.

Fig. 8Receptances determined experimentally and with numerical models

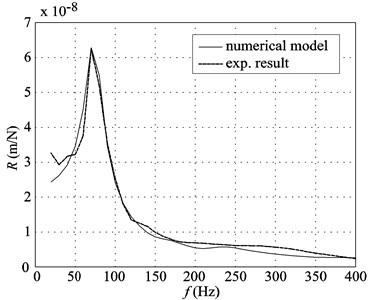
a) Traditional ballasted track

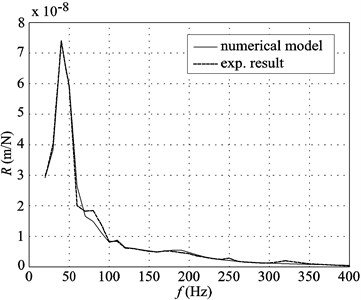
b) STEDEF track

The agreement between the numerical results and the experimental results is satisfactory not only in the traditional track but also for the STEDEF track. In fact, these measurements and the comparison have been of great interest, as these two track types are the most frequently used in the FCMB. These experimental validations show the suitability of the developed numerical models for describing the vibratory behavior of the railway track types considered.

According to the described results, it is noted that both types of tracks tested show only one natural frequency. This is due to the very high stiffness of the fasteners under the rails for these two experimental cases.

Fig. 9Comparison between the experimental receptances at both rails

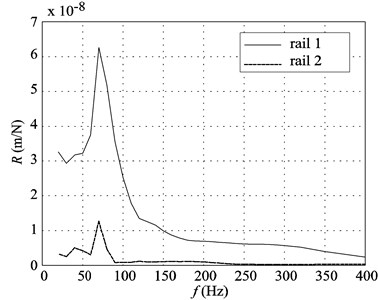
a) Traditional ballasted

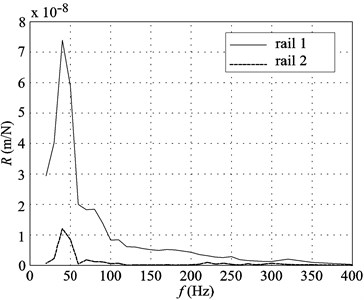
b) STEDEF track

Finally, the last two figures (Figs. 9(a) and 9(b)), show the experimental receptance at the point where the exciting force is applied, rail 1, and the cross receptance defined in the opposite rail, just in front of the excitation point, rail 2.

As in the previous numerical results resumed in Figs. 6(a) and 6(b), the low vibration transmission occurring between both rails for the two types of track is evident.

6. Conclusions

The comparison of the frequency response with the analytical results of the DFF track and the bi-block slab track presents a very good concordance. Similar results have been obtained through the use of different methodologies. This proves the validity of the developed numerical models.

It is found that the numerical models which describe a complete railway track allow for new aspects of the track vibratory behavior to be studied, such as the link between the vibration levels at various positions on the track, which cannot be provided by other models. For example, by means of the numerical models for entire tracks and using the defined parameters, it has been proven that no appreciable interaction occurs between the two rails throughout the track superstructure.

There is good concordance, in the case of the tracks analyzed, between the numerically calculated receptances and those obtained experimentally. This result also confirms the validity of the numerical models used.

The experimental results, as shown in the numerical ones, confirm that the transmission of vibration, from one rail to another through the track superstructure, is weak.

Numerical models of railway tracks combined with a numerical model of the wheelset system provide numerical models of the vibration generation mechanism due to wheel-rail contact. These models will be used in the development of vibration monitoring techniques and will be available to be included in global models of generation and transmission of vibrations due to railway transit. Contact force and rail vibration time histories have been obtained for several track types using the generation models. The models as well as the obtained results will be presented in a forthcoming paper.