Comparison of hydraulic and pneumatic damping of driver’s seats

1. Introduction

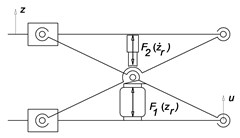
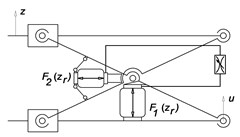
The springing support of driver seat (Fig. 1(a)) consists of a guide mechanism in which is placed a pneumatic spring. Parallel to the air spring is in a guide mechanism connected to a damper (Fig. 1(b)). Force effects $F_1\left(z_r\right)$ and $F_2\left({\dot{z}}_r\right)$ are phased shifted by $\pi /2$.

Fig. 1a) Vehicle driver´s seat, b) Springing seat support with a hydraulic damper, c) Springing seat support with two air springs

a)

b)

c)

In the original author’s solution there are two air springs which by themselves force’s effects acts against each together. They are pneumatically connected through the throttle valve, which achieves phase shifting their force effects $F_1\left(z_r\right)$ and $F_2\left(z_r\right)$ and thereby damping oscillatory motion (Fig. 1(c)).

When the vehicle is moving, the seat is kinetically energized by the movement of the floor. The excitation function $\mathrm{u}$ is in fact in respect frequency and amplitude very diverse and its character depends on the road surface, vehicle suspension and on the speed. Driver’s seats producers asses the dynamic properties of the springing support and the vibration insulation effect based on their own practices and policies. It is usual measurement and evaluation of the feedback $z$ to the excitation signal $u$ which is measured when the vehicle is driving on the test polygon. General evaluation enabling an objective comparison of driver’s seats from different manufacturers in terms of vibration insulation efficiency is practically non-existent.

2. Mechanical model

The basis for evaluating the driver's seat suspension system is undoubtedly the creation and compilation of mechanical model and solving equations of motion.

For commonly known system of Fig. 2 the equation of motion can be written for simplifying assumptions of linearization dynamic parameters in the form:

where $m$ is the reduced mass of moving parts of the seat including the driver, $b$ is the coefficient of vibration damper damping, $k$ is the spring stiffness and a $i_b$ and $i_k$ are the springs and dampers transfers, $u\left(t\right)$ is the displacement of the base under the kinematic excitation, $z\left(t\right)$ is the absolute displacement of the object.

Eq. (1) is possible to write:

where $z_r\left(t\right)$ is the relative displacement of the object and the base.

For pneumatically – mechanically system according Fig. 3 is possible to write equation of motion in the form:

where $b_{constr}$ is construction damping coefficient, $i_1$ and $i_2$ are transfers of springs in mechanism.

The springs of the resilient differential pneumatic support have their geometrical characteristics given by polynomial functions of effective surfaces $S_1\left(z_{p1}\right)$ and $S_2\left(z_{p2}\right)$ and volumes $V_1\left(z_{p1}\right)$ and $V_2\left(z_{p2}\right)$. The forces in the springs are also:

There are $z_{p1}$ and $z_{p2}$ deformations of the springs, $p_{p1}$ and $p_{p2}$ air pressures in the springs and $S_1\left(z_{p1}\right)$ and $S_2\left(z_{p2}\right)$ effective surfaces of the springs. The equation of motion of the support with the mass $m$ of the supported object is simple:

where $z_r\left(t\right)$ is the relative displacement of the object and the base, $u\left(t\right)$ is the displacement of the base under the kinematic excitation, $z\left(t\right)$ is the absolute displacement of the object, $b_{constr}$ is the construction damping of the mechanism, $mg$ is the static load of the mechanism. The function $F\left(z_r\right)$ is the equivalent force from the springs:

where $i_1\left(z_r\right)$ and $i_2\left(z_r\right)$ are transmission ratios of the springs.

Air pressures inside the springs obey the state equation of ideal gas:

where $m_{a1}$ and $m_{a2}$ are masses of the air enclosed inside the springs, $r$ is specific gas constant and $T_1$, $T_2$ are temperatures of the air inside the springs.

The air exchange between the springs is described by isentropic air flow through the throttle valve. In the next two equations, the rate of air exchange depends on pressures $p_A$ and $p_B$; the pressure $p_A$ signs the higher pressure of $p_{p1}$, $p_{p2}$ at a given time, $p_B$ is the other one. Which of the two pressures is higher determines the sign of the flow rate. The rate of air mass is then:

for subcritical flow conditions, where $p_B/p_A\ge {\beta }^{*}$ or:

otherwise. Critical pressure ratio ${\beta }^{*}$is:

where $\kappa$ is specific heat ratio for the air. In the Eqs. (9) and (10) are $c$ discharge coefficient and $A_v$ cross-section of the throttle valve.

Differential Eq. (8) supplemented by differential equation for air mass inside the springs describe the presented pneumatic-mechanical system. We have considered closed pneumatic system, so the air masses are bound by condition:

Having the thermal effects in the scope of this article, the temperatures $T_1$, $T_2$ are considered as state variables. The evolution of the air temperatures in time is described by following differential equations derived from internal energy conservation (first law of thermodynamics):

where $c_v$ is isochoric thermal capacity of the air, $T_{\infty }$ is the ambient temperature and ${\alpha }_T$ is the coefficient of heat transfer.

3. Comparison of hydraulic and pneumatic damping

Based on solutions of equations of motion in the preceding paragraph a transmission frequency characteristic can be obtained which are usually concerned to displacement amplitude of the oscillatory movement of the seat. According to these data can evaluate the function of the spring base due to changes in the position of the driver to the vehicle controls and set the appropriate size of the damping coefficient.

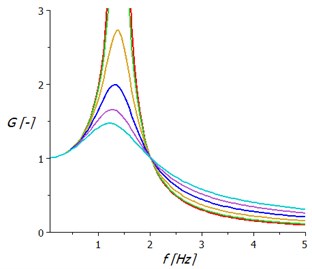
In case the springing support with hydraulic damper according to Fig. 1(b) the transmission frequency characteristics are based on as shown on Fig. 2(a).

Particular damping characteristics correspond to the relative damping coefficient of 0.01 and 0.1 to 0.5 with step 0.1. Generally, it is possible to say, the damping has a positive effect when the system is erected near to its natural frequency. Outside of this region is the damping importance with respect to the displacement amplitude small to rather negative.

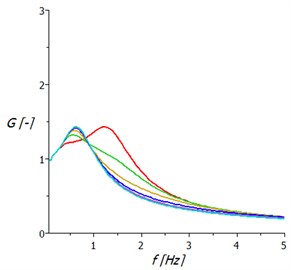
In case the springing support according to Fig. 1(c) are the transmissions frequency characteristics based on as is shown on Fig. 2(b).

Fig. 2Transmission frequency characteristics of springing support: a) with hydraulic damper, b) with two air springs

a)

b)

Individual characteristics correspond to different intensities throttling the flow of compressed air between the two air springs of the support. The diameters of the holes are graded from 1 mm to 3.5 mm with step 0.5 mm. The damping character of the oscillation is in this case favourable in the wider frequency range and the gain does not exceed the value 1.5.

Another criterion of driver seat vibration insulation evaluation properties is acceleration value and frequency, which act on the driver and adversely affect the driving comfort.

In Fig. 3(a) are acceleration transmission frequency characteristics of springing support with linear hydraulic damper. It shows that damping is decreasing displacement amplitude, but significantly increases the acceleration values. This fact requires vibration insulation systems seats which show outside the resonance region negligible damping.

Fig. 3Acceleration amplitude frequency characteristics of springing support: a) with hydraulic damper, b) with two air springs

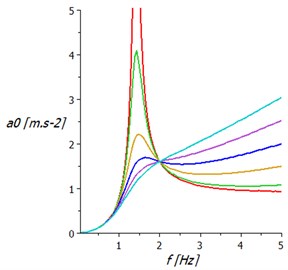
a)

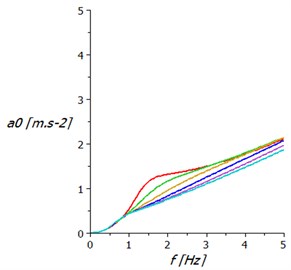
b)

In Fig. 3(b) are the acceleration amplitude frequency characteristics of springing support with two air springs.

This springing system significantly reduces amplitude acceleration values compared to the classic springing support design. Acceleration amplitudes increase almost linearly with excitation frequency.

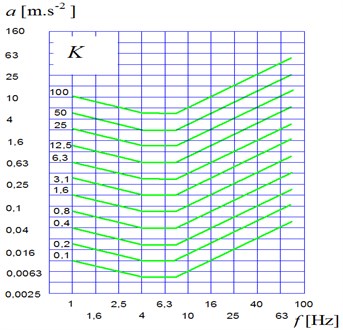
Vibration isolation properties of the driver seat can be quantified on the basis of hygiene standards. There is medical research, where the result is the definition of sitting person’s comfort under the influence of acceleration of a certain amplitude and frequency. In Fig. 4 are graphs taken from the internationally valid standards ISO 2631, ISO 5982 and VDI 2057.

Using these findings could contribute to an objective evaluation of vibration insulation properties of driver seats and to remove the element of subjective assessment, which currently dominates among the manufacturers of driver seats.

Fig. 4The amplitude and frequency dependence of the sitting human comfort on acceleration

Using the coefficient $K$ the vibration insulation level of the driver seat properties can be deduced. In Fig. 5(a) dependence the coefficient $K$ is calculated on seat’s excitation frequency with hydraulic telescopic shock absorber and Fig. 5(b) shows this dependence on the seat with two pneumatic springs.

Fig. 5Frequency dependence the coefficient of seated human loading on the acceleration of seat: a) with hydraulic telescopic shock absorber, b) with two air springs

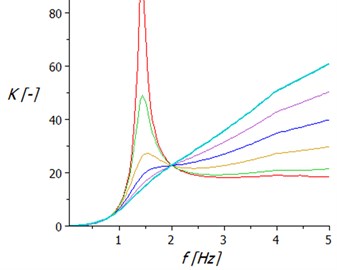
a)

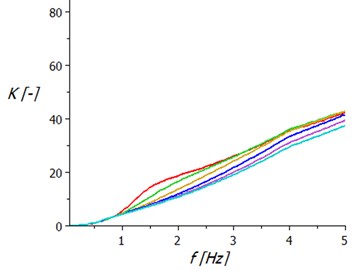
b)

4. Conclusion

There are many technical problems that are connected with a necessity of the minimization of the vibrations, especially in the automotive industry. There are many types of equipment which have an excitation through the movement of the foundation. The typical instance of this set is a driver seat. With vibration isolation of these objects, there are further problems that come from variable excitation frequency. It is clear that the condition of the sufficient difference between the force excitation frequency and resonant frequency of the dynamic systems cannot be ensured at all times. In these cases, it is necessary to use special supports with the possibility of the stiffness changing, and to tune the natural frequency of the system appropriately. In the paper are presented two possibilities of the driver’s seat design. One of them is the classical solution with a hydraulic damper. The second one is an original solution of authors which has two pneumatic springs in the guide mechanism.

This original solution presents a pneumatic spring system with a differential configuration and the throttling of the air flow between the springs. The springs act one against the other. This system can be used with benefits to the vibration isolation of the objects of the systems with kinematic excitation, e.g. driver seats, ambulance couchettes, etc. Based on the frequency spectrum of excitation, it is possible to choose the optimum cross-section of the throttling element and achieve efficient damping of vibration in a relatively broad range of low excitation frequencies. Similar results can be seen by measurement of the real system. Evaluation of both seats is made on the basis of simulation of vibration excitation at constant amplitude support displacements at frequencies from 0 to 5 Hz. The obtained frequency characteristics of kinematic quantities are further processed for the purpose the sitting human loading of vertical acceleration coefficient determination. Calculation results showed that a qualitatively higher level of vibration insulation properties seat has the seat with two air springs.