Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Li, Yuehan; Nguyen, Vanliem; Guo, Xiaoyan; Kang, Yan

doi:10.21595/jmai.2021.21861

Journal of Mechatronics and Artificial Intelligence in Engineering

Browse Journal

Submit article

Published: 16 February 2021

Check for updates

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li¹

Vanliem Nguyen²

Xiaoyan Guo³

Yan Kang⁴

^{1, 2, 3, 4}School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi, 435003, China

^{1, 2, 3, 4}Hubei Key Laboratory of Intelligent Conveying Technology and Device, Hubei Polytechnic University, Huangshi, 435003, China

Corresponding Author:

Vanliem Nguyen

Cite the article Download PDF

Downloads 831

Abstract

In order to further enhance the ride quality of vibratory roller’s cab used by the hydro-pneumatic mounts (HPM), based on a nonlinear dynamics model of the vibratory rollers under interaction of the deformable terrain and drum established based on Matlab/Simulink software, a semi-active cab’s HPM of vibratory rollers are then controlled by using the Fuzzy controller. The root-mean-square (RMS) of the accelerations of the vertical driver’s seat and the cab’s pitch angle have been used as objective studies. The research results indicate that the ride comfort of the driver's seat and the shaking of the cab are greatly affected under the deformable soil grounds, especially under a soft soil ground. However, with the HPM using the Fuzzy control, the RMS accelerations of the driver’s seat and cab pitch angle have been remarkably decreased by 40.1 % and 22.2 % under a hard soil ground. Therefore, the ride quality of the vibratory roller has been enhanced by the semi-active HPM.

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Highlights

A semi-active cab's HPM of vibratory rollers are then controlled by using the Fuzzy controller further enhance the ride quality of vibratory roller's cab used by the hydro-pneumatic mounts.
The root-mean-square (RMS) of the accelerations of the vertical driver's seat and the cab's pitch angle have been used as objective studies.
The research results indicate that the ride comfort of the driver's seat and the shaking of the cab are greatly affected under the deformable soil grounds, especially under a soft soil ground.
Especially, the RMS accelerations of the driver's seat and cab pitch angle have been remarkably decreased by 40.1 % and 22.2 % under a hard soil ground.

1. Introduction

The vibratory rollers often work in factories and construction site, and its operation process includes a combined static and dynamic forces of all the vehicle and the drum to compress the asphalt, terrain, or other materials. The vibration excitations from the deformable terrain and the drum are thus transmitted the driver via the cab and the vehicle's isolation systems [1-3]. Consequently, in the design process of the vibratory rollers often, the designer always wants the vertical excitations from the drum impacting on the terrain ground to be maximum, and the vibration sources from the vehicle frame transmitted to the cab floor via isolation mounts to be minimum.

Basic research of interaction models of the tyre-soft soil and of the drum-elastoplastic soil showed that the responses the vehicle vibration had been greatly influenced by off-road soil grounds [4-6]. The excitations from off-road terrains and the vibratory drum were almost transmitted to the cab floor via its isolation system and the driver’s drive via its suspension. Consequently, the isolation system of the cab is one of the most important indexes for improving the vehicle's ride quality.

The cab’s isolation system of the vibratory rollers equipped with the hydraulic mounts has been researched and controlled [7-10]. The study results indicated that the ride quality of the vehicle had been greatly improved by semi-active hydraulic mounts. However, the results also showed that vibrations heave of the driver’s seat and the shaking of the cab were still high under various operating conditions. Therefore, to enhance the ride quality of the vehicle and control the shaking of the cab, a combination of the hydraulic and pneumatic mounts for the cab of vibratory rollers was proposed and studies [11, 12]. The combination results between the rubber mounts (RM), hydraulic mounts (HM), and hydro-pneumatic mounts (HPM) in Part 1 showed that the HPM improved the ride comfort of the vibratory roller cab is better than both isolation of the RM and HM. However, the vibrations of the driver’s seat heave and the cab shaking were also still great under various operating conditions. To solve this issue, to control the HPM is necessary. The control method of the Fuzzy control were also applied to control the hydraulic mounts of the soil compactor cab or the vehicle suspension systems [8, 9, 13]. The control results significantly reduced the vehicle vibrations. Thus, the Fuzzy control can be also applied to control the HPM of the vibratory roller cab.

In this research, based on the model of the vibratory roller and deformable terrain interaction, and the dynamics model of the vibratory rollers built under the vibration excitations consisted by the drum/tires-deformable terrain contact in the condition of the vehicle traveling; and of an excitation of the drum 28 Hz in the condition of the vehicle working in an elastic/plastic ground in Part 1. A semi-active hydro-pneumatic mounts (HPM) controlled based on the Fuzzy control to further enhance the ride comfort of the vibratory roller is then researched and applied. The performance of the semi-active HPM is then evaluated via the weighted RMS accelerations of the driver’s seat and the cab’s pitch angle under two working conditions of the hard and soft soil grounds.

2. The dynamics model of vibratory rollers

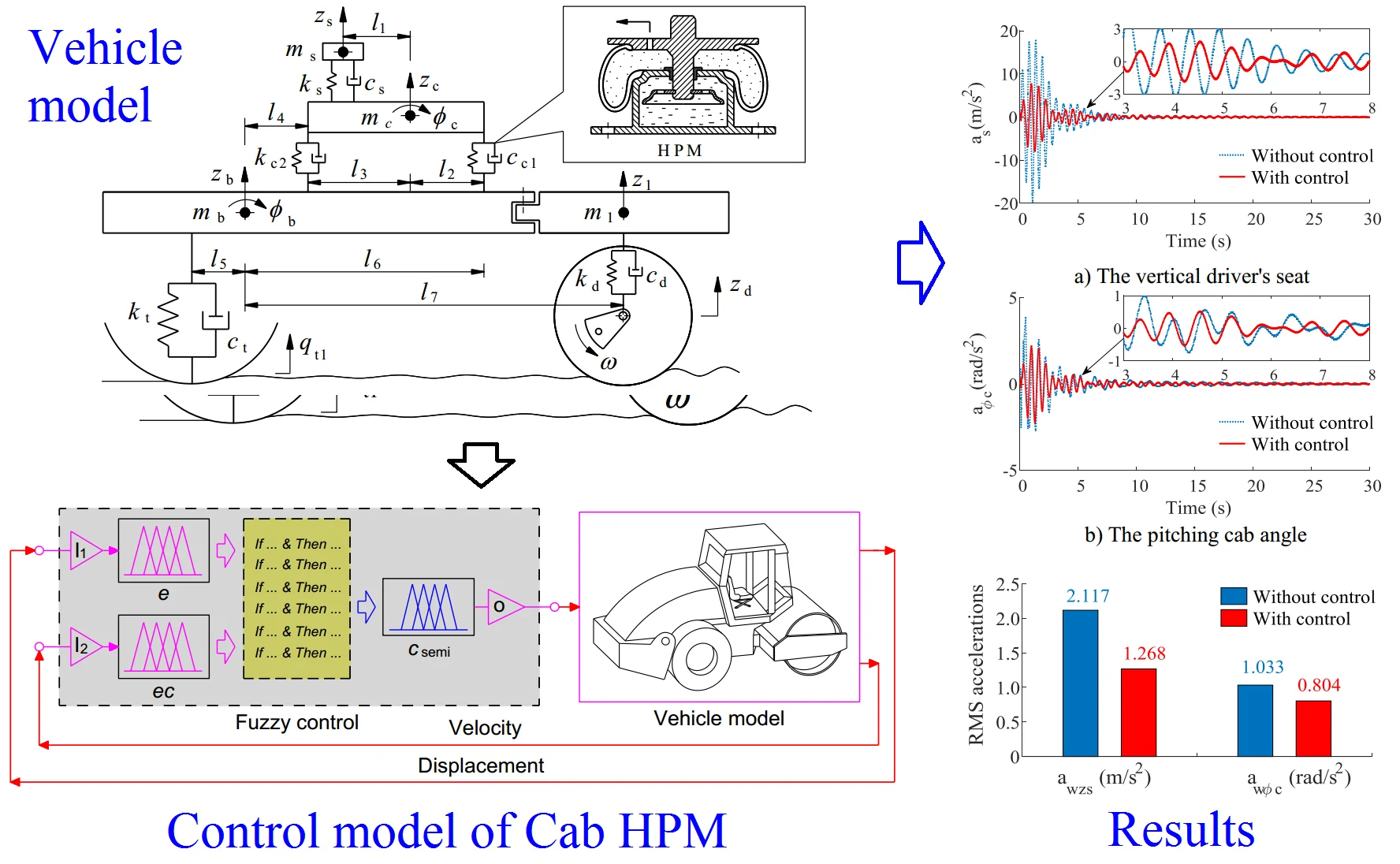
The vibratory roller is mainly composed of the wheel, body, cab, seat, and vibrator drum, among which cab and rear vehicle frame are mainly connected through the cab isolation systems to improve the vehicle’s ride comfort. The vibration system of vibratory roller is composed of vibration mechanism, steel drum, shock absorber, drive plate and vibration frame. The vibration mechanism is the force source of vibration of the vibratory roller, and the centrifugal force generated when the vibratory axis rotates is the vibratory force of the vehicle. Based on the actual vehicle structure, the nonlinear dynamic model of vehicle is modeled as in Fig. 1, where, $z_{b}$ , $z_{1}$ , $z_{c}$ , and $z_{s}$ are the vertical displacement of the rear frame, front frame, cab, and seat; $z_{d}$ is the vertical displacement of the flat section of the drum-ground contact surface; $m_{b}$ , $m_{1}$ , $m_{c}$ , and $m_{s}$ are the weights of the rear frame, front frame, cab, and seat; $I_{b}$ and $I_{c}$ are the moment of inertia of the rear frame and the cab; $k_{s}$ , $k_{c 1}$ , and $k_{c 2}$ are the stiffness of the vibration isolators of the seat, front and rear cab, respectively; $c_{s}$ , $c_{c 1}$ , and $c_{c 2}$ are the damping of the vibration isolators of the seat, front and rear cab, respectively; $q_{t 1}$ is excitation of the road roughness; $ϕ_{c}$ and $ϕ_{b}$ are the cab and rear frame's pitch angles; $l_{1}$ , $l_{2}$ , $l_{3}$ , $l_{4}$ , $l_{5}$ , $l_{6}$ , and $l_{7}$ are the geometric dimensions.

Fig. 1The nonlinear dynamics model of vibratory rollers

Based on the vehicle dynamics model, the dynamic differential equation is given by:

1

m_{s} {\ddot{z}}_{s} = c_{s} ({\dot{z}}_{c} + {\dot{ϕ}}_{c} l_{1} - {\dot{z}}_{s}) + k_{s} (z_{c} + ϕ_{c} l_{1} - z_{s}),

2

m_{c} {\ddot{z}}_{c} = c_{c 1} ({\dot{z}}_{b} + {\dot{ϕ}}_{c} l_{2} - {\dot{ϕ}}_{b} l_{6} - {\dot{z}}_{c}) + k_{c 1} (z_{b} + ϕ_{c} l_{2} - ϕ_{b} l_{6} - z_{c}),

3

m_{1} {\ddot{z}}_{1} = c_{d} ({\dot{z}}_{d} - {\dot{z}}_{1}) + k_{d} (z_{d} - z_{1}),

4

m_{b} {\ddot{z}}_{b} = c_{t} ({\dot{q}}_{t 1} - {\dot{ϕ}}_{b} l_{5} - {\dot{z}}_{b}) + k_{t} (q_{t 1} - ϕ_{b} l_{5} - z_{b}) = 0,

5

I_{c} {\ddot{ϕ}}_{c} = l_{3} [c_{c 2} ({\dot{z}}_{b} - {\dot{z}}_{c} - {\dot{ϕ}}_{c} l_{3} - {\dot{ϕ}}_{b} l_{4}) + k_{c 2} (z_{b} - z_{c} - ϕ_{c} l_{3} - ϕ_{b} l_{4})]

+ l_{2} [c_{c 1} ({\dot{z}}_{c} - {\dot{z}}_{b} - {\dot{ϕ}}_{c} l_{2} + {\dot{ϕ}}_{b} l_{6}) + k_{c 1} (z_{c} - z_{b} - ϕ_{c} l_{2} + ϕ_{b} l_{6})]

+ l_{1} [c_{s} ({\dot{z}}_{s} - {\dot{z}}_{c} + {\dot{ϕ}}_{c} l_{1}) + k_{s} (z_{s} - z_{c} + ϕ_{c} l_{1})],

6

I_{b} {\ddot{ϕ}}_{b} = l_{5} [c_{t} ({\dot{q}}_{t 1} - {\dot{z}}_{b} - {\dot{ϕ}}_{b} l_{5}) + k_{t} (q_{t 1} - z_{b} - ϕ_{b} l_{5})]

- l_{4} [c_{c 2} ({\dot{z}}_{c} - {\dot{z}}_{b} + {\dot{ϕ}}_{c} l_{3} + {\dot{ϕ}}_{b} l_{4}) + k_{c 2} (z_{c} - z_{b} + ϕ_{c} l_{3} + ϕ_{b} l_{4})]

- l_{6} [c_{c 1} ({\dot{z}}_{c} - {\dot{z}}_{b} - {\dot{ϕ}}_{c} l_{2} + ϕ_{b} l_{6}) + k_{c 1} (z_{c} - z_{b} - ϕ_{c} l_{2} + ϕ_{b} l_{6})]

- l_{7} [c_{d} ({\dot{z}}_{1} - {\dot{z}}_{d}) + k_{d} (z_{1} - z_{d})] .

3. Semi-active cab hydro-pneumatic mount of the cab

Based on the research results in Part-1, the three types of isolation systems including the rubber mounts (RM), the hydraulic mounts (HM), the hydro-pneumatic mounts (HPM) are compared. The results showed that the HPM is the best on improving the ride comfort. Therefore, to further improve the ride comfort of the vibratory roller, this paper proposes the semi-active HPM controlled by using Fuzzy control to enhance the ride comfort of the vehicle. The model of the semi-active HPM is indicated as in Fig. 2, where, $k_{v}$ and $k_{e}$ are the linear stiffness of the HPM, $c_{β}$ is the main damping coefficient of the HPM mounts, and $c_{s e m i}$ is the variable damping coefficient. Liquid damping force $f_{d} = c_{h} |\dot{z}| \dot{z}$ is expressed by quadratic nonlinear damping characteristics, including $c_{h}$ on behalf of the coefficient of the hydro-pneumatic damping mounts, $ζ$ is the air’s move in the pipe.

Fig. 2The mathematical model of the passive and semi-active HPM of the cab

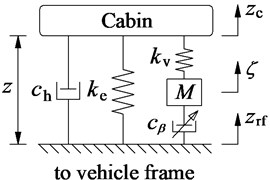
a) Passive HPM

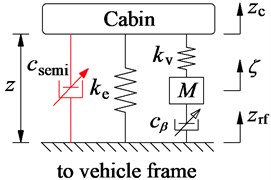
b) Semi-active HPM

The corresponding vertical dynamic forces of the front and rear isolations are given as follows [8, 11]:

7

F_{c i} = k_{e i} ({\dot{z}}_{c i} - {\dot{z}}_{r f i}) + c_{β i} {|ζ_{i}|}^{β i} s i g n ({\dot{ζ}}_{i}) + M_{i} {\ddot{ζ}}_{i} + f_{d i},

8

f_{d i} = \{\begin{array}{l} c_{h i} |{\dot{z}}_{c i} - {\dot{z}}_{r f i}| ({\dot{z}}_{c i} - {\dot{z}}_{r f i}), \\ c_{h i} |{\dot{z}}_{c i} - {\dot{z}}_{r f i}| ({\dot{z}}_{c i} - {\dot{z}}_{r f i}) + c_{s e m i - i} ({\dot{z}}_{c i} - {\dot{z}}_{r f i}), \end{array} \begin{array}{l} with HPM, \\ with SHM, \end{array}

9

z_{c i} = z_{c i} + (- 1)^{i + 1} ϕ_{c} l_{i + 1}, {\dot{z}}_{c i} = {\dot{z}}_{c i} + (- 1)^{i + 1} {\dot{ϕ}}_{c} l_{i + 1},

10

\{\begin{array}{l} z_{r f 1} = z_{b} + (l_{2} + l_{3} + l_{3}) ϕ_{b}, \\ z_{r f 2} = z_{b} - l_{5} ϕ_{b}, \end{array} \{\begin{array}{l} {\dot{z}}_{r f 1} = {\dot{z}}_{b} + (l_{2} + l_{3} + l_{3}) {\dot{ϕ}}_{b}, \\ {\dot{z}}_{r f 2} = {\dot{z}}_{b} - l_{5} {\dot{ϕ}}_{b}, \end{array}

where, $z_{c i}$ and $z_{r f i}$ are the vertical displacements of suspension of cab and front and rear frames, $i =$ 1, 2.

4. Application of the Fuzzy control for the HPM

The fuzzy logic controller was incepted by Zadeh in 1965. It is then widely applied in variety situations as well as diverse fields. A fuzzy logic-based control for semi-active suspension of vehicle is suggested and the capabilities for the improvement of ride comfort are studied through the software simulation. In this study, to control the semi-active HPM, the fuzzy control is designed and then applied to control the damping coefficient of the HPM.

The fuzzy logic controller consists of a fuzzification interface, a fuzzy inference system and a defuzzification interface. First, the crisp values in fuzzification are transformed into linguistic variables. The fuzzy inference system is then used by the fuzzy rule in accordance with the inference rule. Finally, the linguistic variables are transformed back to crisp values through defuzzification for use by the physical plant of the air suspension system [13-15]. Herein, the relative displacement z and the relative velocity $\dot{z}$ of the HPM in Fig. 2(b) are considered as two input variables while the damping coefficient $c_{s e m i}$ is the output of the fuzzy control. The control model is plotted in Fig. 3.

Fig. 3The model of the Fuzzy control for the HPM

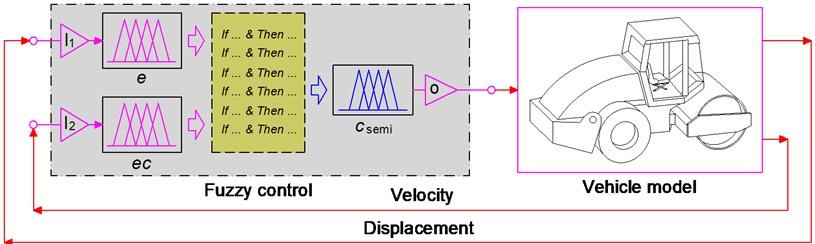
The nine value of the linguistic variables of input/output signals are defined by the positive very big (PVB), positive big (PB), positive medium (PM), positive small (PS), zero (Z), negative small (NS), negative medium (NM), negative big (NB), negative very big (NVB) and $y_{i}$ ( $i =$ 1, 2, …, 9).

Fig. 4Membership functions for input and output variables of the PHM

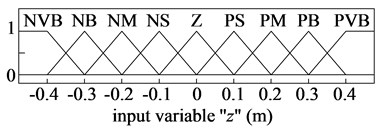
a) The relative displacement $z$

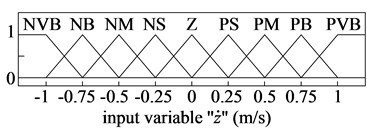
b) The relative velocity $\dot{z}$

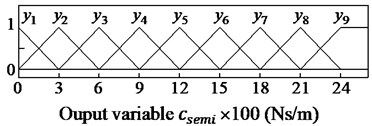
c) The damping coefficient $c_{s e m i}$

The membership functions for input and output variables of the semi-active HPM have been represented via a fuzzy set. The shape of membership functions is the triangular function and the value of the degree of memberships is between 0 and 1, as shown in Fig. 4.

In this fuzzy controller, the rules of “if-then” are used to define the relationship of $z$ , $\dot{z}$ and $c_{s e m i}$ according to the designers’ knowledge and experience, the fuzzy controller has all 81 possible rules listed in Table 1.

To calculate the control results of the fuzzy controller, the fuzzy inference system is applied by the minimum function and the centroid method of Mamdani [15, 16]. In this paper, Mamdani’s fuzzy inference system is used to control the semi-active HPM.

Table 1Rules for fuzzy control

$\dot{z}$	$z$
$\dot{z}$	NVB	NB	NM	NS	Z	PS	PM	PB	PVB
NVB	$y_{5}$	$y_{9}$	$y_{7}$	$y_{6}$	$y_{5}$	$y_{4}$	$y_{4}$	$y_{3}$	$y_{3}$
NB	$y_{3}$	$y_{5}$	$y_{8}$	$y_{6}$	$y_{5}$	$y_{4}$	$y_{3}$	$y_{3}$	$y_{3}$
NM	$y_{1}$	$y_{2}$	$y_{5}$	$y_{7}$	$y_{5}$	$y_{3}$	$y_{3}$	$y_{3}$	$y_{2}$
NS	$y_{1}$	$y_{1}$	$y_{1}$	$y_{5}$	$y_{5}$	$y_{3}$	$y_{2}$	$y_{2}$	$y_{2}$
Z	$y_{1}$	$y_{1}$	$y_{1}$	$y_{1}$	$y_{5}$	$y_{1}$	$y_{1}$	$y_{1}$	$y_{1}$
PS	$y_{2}$	$y_{2}$	$y_{2}$	$y_{3}$	$y_{5}$	$y_{5}$	$y_{1}$	$y_{1}$	$y_{1}$
PM	$y_{2}$	$y_{3}$	$y_{3}$	$y_{3}$	$y_{5}$	$y_{7}$	$y_{5}$	$y_{2}$	$y_{1}$
PB	$y_{3}$	$y_{3}$	$y_{3}$	$y_{4}$	$y_{5}$	$y_{6}$	$y_{8}$	$y_{5}$	$y_{3}$
PVB	$y_{3}$	$y_{3}$	$y_{4}$	$y_{4}$	$y_{5}$	$y_{6}$	$y_{7}$	$y_{9}$	$y_{5}$

5. Simulations and discussions

5.1. Evaluation index

In the vehicle working process, the uneven road surface and rotating parts such as engine, transmission system, and wheels will stimulate the vibration of the vehicles. The vehicle’s ride comfort is mainly to maintain the impact of the vibration and impact environment generated in the driving process on the ride comfort of passengers. Within a certain range, each person's psychological and physical qualities are different, so the sensitivity to vibration is very different. Therefore, the basic evaluation method of the weighted root-mean-square value of acceleration is used to evaluate the impact of vibration on the human's ride comfort and health, as follows [8]:

11

a_{w} = \sqrt{T^{- 1} \int_{0}^{T} a_{w}^{2} (t) d t},

where, $a_{w} (t)$ is the weighted acceleration time history recorded by $a (t)$ obtained through the simulation process; $T$ is the analysis time of vibration.

5.2. Analysis results

To evaluate the performance of the semi-active HPM, based on the lumped parameters of the vibratory roller and cab isolation mounts in Part-1 listed in Tables 2 and 3, a single-drum vibratory roller compacting and moving at the excitation frequency of the drum 28 Hz and 5 km/h on two different grounds of the hard and soft soils is simulated and controlled by using Fuzzy controller. The simulation results of the acceleration responses of the vertical driver and pitching cab angle are plotted in Figs. 5 and 6.

Table 2The lumped parameters of the vibratory rollers

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$m_{s}$ / kg	85	$I_{r f y}$ / kgm²	1.2×10⁴	$l_{1}$ / m	0.383	$k_{s}$ / N m^-1	1.2×10⁴
$m_{c}$ / kg	891	$I_{f f x}$ / kgm²	1.9×10³	$l_{2}$ / m	0.1	$k_{d 1,2}$ / N m^-1	3.9×10⁶
$m_{f f}$ / kg	2822	$I_{d x}$ / kgm²	3.0×10³	$l_{3}$ / m	0.524	$k_{t 1,2}$ / N m^-1	0.5×10⁶
$m_{f r}$ / kg	4464	$b_{1}$ / m	0.55	$l_{4}$ / m	0.136	$c_{s}$ / Ns m^-1	1.2×10²
$m_{d}$ / kg	4378	$b_{2}$ / m	0.7	$l_{5}$ / m	0.76	$c_{d 1,2}$ / Ns m^-1	2.9×10³
$I_{c x}$ / kgm²	560	$b_{3}$ / m	0.68	$l_{6}$ / m	0.9	$c_{t 1,2}$ / Ns m^-1	4.0×10³
$I_{c y}$ / kgm²	523	$b_{4}$ / m	0.945	$l_{7}$ / m	0.6	$f$ / Hz	28
$I_{r f x}$ / kgm²	3.1×10³	$b_{5}$ /m	0.945	$l_{8}$ /m	1.5	$v_{0}$ / km h^-1	5

Table 3The lumped parameters of the cab’s HPM

Parameter	Value	Parameter	Value	Parameter	Value
$k_{r 1,2}$ / Nm^-1	9.1×10⁵	$k_{v 1,2}$ / Nm^-1	15.3×10⁵	$c_{β 1,2}$ / Ns²m^-2	12.4×10³
$k_{r 3,4}$ / Nm^-1	1.2×10⁵	$k_{v 3,4}$ / Nm^-1	2.01×10⁵	$c_{β 3,4}$ / Ns²m^-2	10.7×10³
$M_{1,2}$ / kg	98	$c_{r 1,2}$ / Nsm^-1	218	$c_{h 1,2}$ / Ns²m^-2	20×10³
$k_{e 1,2}$ / Nm^-1	9.1×10⁵	$c_{r 3,4}$ / Nsm^-1	29	$c_{h 3,4}$ / Ns²m^-2	4.5×10³
$k_{e 3,4}$ / Nm^-1	1.2×10⁵	$M_{3,4}$ / kg	33

Fig. 5The acceleration responses under a hard soil

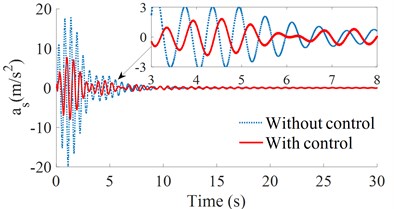
a) The vertical driver’s seat

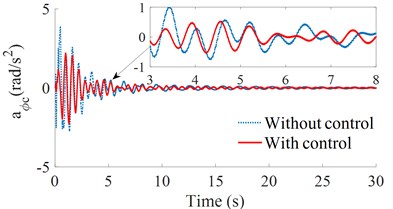
b) The pitching cab angle

Fig. 6The acceleration responses under a soft soil

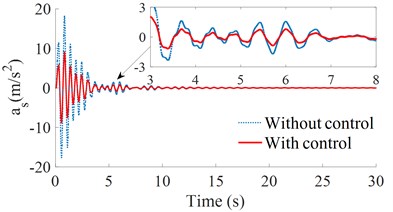
a) The vertical driver’s seat

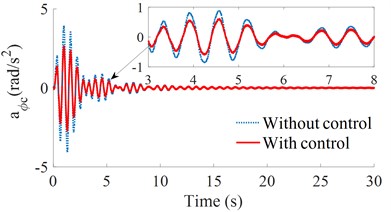
b) The pitching cab angle

By analyzing the images and data in Figs. 5 and 6, it can see that, on the ground of the hard soil, the isolation mounts of the HPM with controlled damping performs better than the uncontrolled isolation mounts, and the values of the crest are also much lower than that of the uncontrolled isolation mounts. Besides, the time to reach the stable fluctuation range is also shorter than that of the uncontrolled HPM, and the advantage of the controlled HPM in the vertical acceleration of the driver's seat is more obvious. On the ground of the soft soil, the controlled damping suspension also has a good control of the vertical driver's seat and cab pitch angle. Therefore, on both the soft or hard soil grounds, the controlled HPM has a better improvement in both the acceleration responses of the vertical driver’s seat and cab pitch angle than the uncontrolled HPM.

Fig. 7The RMS acceleration responses of the cab and driver’s seat

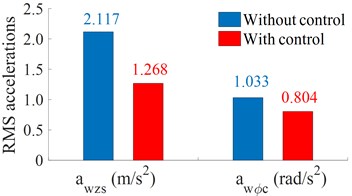
a) Under a hard soil ground

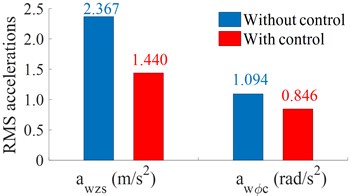
b) Under a soft soil ground

According to the chart and recorded data of the simulation process, the RMS acceleration responses of the cab and driver's seat are also shown in Fig. 7. The comparison results show that the vertical acceleration of the driver's seat with control is greatly reduced by 40.1 % compared to the HPM without control, and the cab pitch angle with control is about 22.2 % less than that of the HPM without control on a hard soil ground. On a soft soil ground, the vertical acceleration of the driver's seat with control is reduced by 39.2 % compared with that without control, and the cab pitch angle with control is lower 22.7 % compared to the HPM without control. This obtained result is due to the damping coefficient $c_{h}$ of the damper mount is optimized by the Fuzzy control in the vehicle competing and working process. Therefore, the controlled HPM can improve the vehicle’s ride comfort under both the hard and soft soil grounds.

6. Conclusions

The data analysis of the hydro-pneumatic mounts and its semi – active of the vibratory roller cab has obtained the corresponding results through simulation and test. By changing the damping through fuzzy control of the HPM, the RMS accelerations of the vertical driver’s seat and the pitching cab angle under various conditions are obtained to evaluate the ride comfort. These research results are summarized as follows:

1) When the vehicle moving at 5 km/h, whether on the hard or soft soil grounds, the damping coefficient $c_{h}$ with control has a better improvement the acceleration vibrations in all the vertical driver’s seat and cab pitch angle than the uncontrolled damping coefficients, especially on the hard soil ground.

2) Under the vehicle working condition at 5 km/h and 28 Hz of the vibrator drum, the RMS accelerations of the driver’s seat and cab pitch angle are greatly reduced by 40.1 % and 22.2 % compared to the HPM without control under a hard soil ground, and by 39.2 % and 22.7 % under a soft soil ground. Therefore, the vehicle’s ride comfort is further improved by using the semi-active HPM.

3) The above analysis result shows that the HPM has outstanding performance in various types of isolation mounts in Part-1, and the semi-active HPM used with the Fuzzy control has superior performance compared to the HPM without control.

References

Adam D., Kopf F. Theoretical analysis of dynamically loaded soils. Proceedings of European Workshop Compaction of Soils and Granular Materials, Paris, France, 2000, p. 207-220.

Search CrossRef
Le V., Zhang J., et al. Experimental modal analysis and optimal design of cab’s isolation system for a single drum vibratory roller. Vibroengineering Procedia, Vol. 31, 2020, p. 52-56.

Publisher
Nguyen V., Zhang J., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 8527574.

Publisher
Mitschke M. Dynamik Der Kraftfahrzeuge. Springer-Verlag, Berlin, Germany, 1972.

Publisher
Wong J. Y. Data processing methodology in the characterization of the mechanical properties of terrain. Journal of Terramechanics, Vol. 17, Issue 1, 1980, p. 13-41.

Publisher
Bekker M. Introduction to Terrain-Vehicle Systems. University of Michigan Press, Ann Arbor, Michigan, USA, 1969.

Search CrossRef
Nguyen V., Nguyen K. Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount. Vibroengineering Procedia, Vol. 21, 2018, p. 89-95.

Publisher
Nguyen V. L., Zhang J. R., et al. Low-frequency performance analysis of semi-active cab’s hydraulic mounts of an off-road vibratory roller. Shock and Vibration, Vol. 2019, 2019, p. 8725382.

Search CrossRef
Nguyen V., Zhang J., et al. Performance analysis of semi-active hydraulic system of the off-road vibratory roller cab using optimal fuzzy-PID control. Journal of Central South University, Vol. 35, 2019, p. 399-407.

Publisher
Nguyen V. L., Zhang J. R., et al. Ride quality evaluation of the soil compactor cab supplemented the auxiliary hydraulic mounts via simulation and experiment. Journal of Central South University, Vol. 35, 2019, p. 273-280.

Search CrossRef
Nguyen V., Zhang J., et al. Low-frequency ride comfort of vibratory rollers equipped with cab hydro-pneumatic mounts. Journal of Southeast University, Vol. 36, 2020.

Search CrossRef
Jiao R., Nguyen V., Le V. Ride comfort performance of hydro pneumatic isolation for soil compactors cab in low frequency region, Journal of Vibroengineering, Vol. 22, 2020, p. 1174-1186.

Publisher
Nguyen V. L., Jiao R. Q., Zhang J. R. Control performance of damping and air spring of heavy truck air suspension system with optimal fuzzy control. International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 4, 2020, p. 179-194.

Publisher
Rao M., Prahlad V. A tunable fuzzy logic controller for vehicle-active suspension systems. Fuzzy Sets and Systems, Vol. 85, 1997, p. 11-21.

Publisher
Karray F., Silva C. Soft computing and intelligent systems design: theory, tools, and application. Addison Wesley, New York, 2014.

Search CrossRef
Mamdani E. Advances in the linguistic synthesis of fuzzy controllers. International Journal of Man-Machine Studies, Vol. 8, 1976, p. 669-678.

Publisher

About this article

Received

06 January 2021

Accepted

04 February 2021

Published

16 February 2021

DOI

https://doi.org/10.21595/jmai.2021.21861

Keywords

vibratory rollers

ride comfort

semi-active hydro-pneumatic mounts

off-road soil grounds

Acknowledgements

This research was supported by Open Fund Project of Hubei Key Laboratory of Intelligent Transportation Technology and Device, Hubei Polytechnic University, China (No. 2020XY105) and Talent Introduction Fund Project of Hubei Polytechnic University (No. 19XJK17R), and Research Project of Hubei Polytechnic University, China (No. 18XJZ05Q).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 18

Ameliorating vibratory roller quality based on two methods of cab’s horizontal damper and cab’s active suspension

Tianyuan Jiang, Vanliem Nguyen, Fan Zhang

Research article

2023 03 13

Improving ride comfort and road friendliness of heavy truck using semi-active suspension system

Hao Li, Vanliem Nguyen

Research article

2020 08 15

Ride comfort performance of hydro pneumatic isolation for soil compactors cab in low frequency region

Renqiang Jiao, Vanliem Nguyen, Vanquynh Le

Research article

2020 06 30

Development of cab isolation systems of off-road vibratory rollers: review research

Vanliem Nguyen, Vanquynh Le

Y. Li, V. Nguyen, X. Guo, and Y. Kang, “Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control,” Journal of Mechatronics and Artificial Intelligence in Engineering, Vol. 2, No. 1, pp. 11–18, Feb. 2021, https://doi.org/10.21595/jmai.2021.21861

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jmai.2021.21861
UR  - https://doi.org/10.21595/jmai.2021.21861
TI  - Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control
T2  - Journal of Mechatronics and Artificial Intelligence in Engineering
AU  - Nguyen, Vanliem
AU  - Li, Yuehan
AU  - Guo, Xiaoyan
AU  - Kang, Yan
PY  - 2021
DA  - 2021/02/16
PB  - JVE International Ltd.
SN  - 2669-1116
ER  - 

Copy Ris

Copied to clipboard!

@article{Nguyen_2021,
	doi = {10.21595/jmai.2021.21861},
	url = {https://doi.org/10.21595/jmai.2021.21861},
	year = 2021,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	author = {Vanliem Nguyen and Yuehan Li and Xiaoyan Guo and Yan Kang},
	title = {Research on ride comfort of vibratory rollers: Part-2 Cab's semi-active {HPM} with fuzzy control},
	journal = {Journal of Mechatronics and Artificial Intelligence in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]V. Nguyen, Y. Li, X. Guo, and Y. Kang, “Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control,” Journal of Mechatronics and Artificial Intelligence in Engineering, Feb. 2021, doi: 10.21595/jmai.2021.21861.

Copy IEEE

Copied to clipboard!

Nguyen, Vanliem, Yuehan Li, Xiaoyan Guo, and Yan Kang. “Research on Ride Comfort of Vibratory Rollers: Part-2 Cab’s Semi-Active HPM with Fuzzy Control.” Journal of Mechatronics and Artificial Intelligence in Engineering, February 16, 2021. https://doi.org/10.21595/jmai.2021.21861.

Copy Chicago

Copied to clipboard!

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Abstract

Highlights

1. Introduction

2. The dynamics model of vibratory rollers

3. Semi-active cab hydro-pneumatic mount of the cab

4. Application of the Fuzzy control for the HPM

5. Simulations and discussions

5.1. Evaluation index

5.2. Analysis results

6. Conclusions

References

About this article

Related Articles