Investigation of longitudinal oscillations warp in the process of changing parameters system

1. Introduction

In [1] it is shown that there is a single class drives characterized in that has two or more media. In particular, concern deck lifting devices fishing vessels to which class of devices. At this point in time most of the hydrobionts produced using trawling. Features of the trawl system devices are well considered in [2, 3].

One of the most likely risks during operation of the system is broken of warps. And, often, to the non-evolutionary nature of the change effort in the rope. The study of non-stationary processes in the “winch-warp-trawl” system is relevant.

2. The purpose

The purpose of this work is study the longitudinal vibrations warp in the process of changing parameters of the system.

Investigated systems “winch-warp-trawl” can be represented as a system with two concentrated masses (the winch drum and the trawl to catch) and warp distributed along the length of the parameters (Fig. 1).

Fig. 1Model of system “winch-warp-trawl”

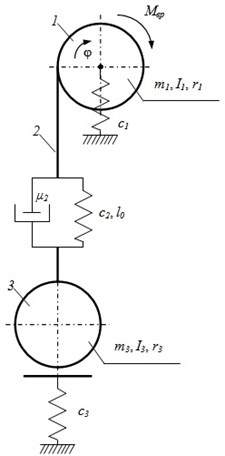
In the figure is indicated: $M_{bp}$ – rotational moment driving the drum; $\phi$ – drum rotation angle; $m_1$, $I_1$, $r_1$ – accordingly the mass, the moment of inertia and the radius of the drum 1; $c_1$ – the stiffness of the drum shaft bearings; ${\mu }_2$, $c_2$, $l_0$ – accordingly the viscous friction coefficient, the stiffness and the starting length of the warp 2; $m_3$, $I_3$, $r_3$ – accordingly the mass, the moment of inertia and the radius of the sphere, which describes the trawl 3; $c_3$ – stiffness of the ground base.

The equations of motion provided by the dynamic model can be written in a general form:

where $F_{upr}$ – the power of warp’s resilience; $R_{tr}$ – the power of the warp’s damping; $F_1=c_1{x}_1$ – resilience power of the drum’s shaft bearings; $N$ – grounds reaction; $R_3$ – trawl’s hydrodynamic resistance; $x_1$ – moving axis of drum; $x_3$ – trawl’s moving.

The power $N$ if the trawl is moving along the ground, a linear dependence of this reaction displacement of the trawl, otherwise it is zero.

The model also takes into account dynamic powers acting in the rope. Thus, the resilient force described by the dependence:

where $l\left(t\right)=l_0-r_1\phi \left(t\right)$, $\mathrm{\Delta }l\left(t\right)=l_0+x_1^{\mathrm{\text{'}}}-x_1\left(t\right)-x_3\left(t\right)$, $E_l$ – modulus of resilience of warp; $F$ – sectional area of the warp; $l\left(t\right)$ – the current length of the warp; $\mathrm{\Delta }l\left(t\right)$ – the distance between the trawl and the middle of a drum; $x_1^{\mathrm{\text{'}}}$ – initial displacement of drum’s axis due to deformation of bearing assemblies.

In [4] was obtained by the mathematical model of motion of the system “trawl winch-warp-trawl” in the form of:

where $I_{pr}=\frac{1}{2}\left(m_1\left(t\right)+\frac{14}{5}{m}_2\left(t\right)\right)r_1{\left(t\right)}^2$ – reduced moment of inertia of the system.

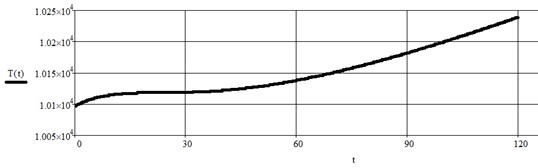
This model takes into account the kinematics of the winch’s drum. In particular, a change of its mass and radius. And also an increase in the mass of the cargo due to increase of production the fish. The results of calculations dynamic loads are in good agreement with the experimental data, showing the "jump" efforts at the time of separation of the trawl from ground (Fig. 2).

Fig. 2The graphical dependence of dynamic loads obtained in result of computer simulation

In the study of the system “warp-trawl” it is necessary to consider damping, inertial and elastic properties that depend on material properties, its geometric characteristics. The powers acting in the system include: weight in water (excluding the weight of the displaced water by the object), elastic powers, inertial powers, powers of hydrodynamic resistance, etc.

In the theory of ropes for evaluation of internal friction using a coefficient of viscous friction, which can be determined from the attenuation of free oscillations or resonance curve for forced oscillation.

The choice of parameters of the cable shall meet the requirements of high tensile strength and sufficient flexibility for the smooth winding of the winch drum fishing vessel. In strength calculations, the basic criterion is the exposure of discontinuous efforts.

Consider the time motion of the system “warp-trawl” in the moment when the trawl approaches jamb and fish accumulates in the bag of the trawl. It is obvious to assume that the most probable law of variation of the weight trawl will be linear, assuming constant speed of the vessel. While warp is carry out longitudinal vibrations. Weight of the trawl much more than the tether mass, so the mass of the latter can be neglected.

Changes the mass of the rope almost does not affect the dynamic processes in the selection of the trawl, therefore, the damping ratio can be taken constant.

In the first stage let us assume that the length of warp remains unchanged and equal $l_0$. Consequently, the stiffness coefficient will be constant.

Then the investigated mechanical system described by the differential equation [7-10]:

This differential equation is linear, one of the coefficients which are variable. For finding analytical solutions of such equations we had earlier proposed method of constant coefficients of the derivative of the new variable [5, 6].

In accordance with this method, we introduce a new variable $z=f\left(t\right)$, tentatively called the defining function. Then the possible transition to a differential equation with constant coefficients and derivatives in the new variable

For the transition to a differential equation with constant coefficients and derivatives in the new variable, we introduce a new variable:

Let the coefficients $C_0$, $C_1$ and $C_2$ will have the form $C_0=m_{30}{k}^2/4$, $C_1=$ 0 and $C_2=c_2$.

With this in mind, Eq. (4) we rewrite in the form:

where ${\omega }_0=\sqrt{c_2/m_{30}}$ – the initial frequency of free oscillations.

Solving the equation obtained by the method of undetermined coefficients, and, turning to the original variable $t$, get the general solution $x_0\left(t\right)$ the corresponding homogeneous equation, which describes the dynamics of the free motion of the system:

Constant values $a$ and $\gamma$ determine, based on the initial conditions:

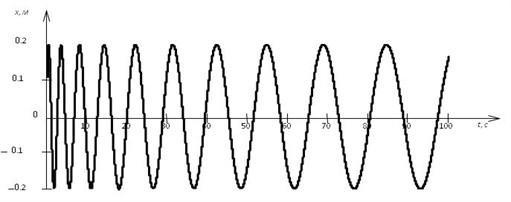
As you can see, this equation describes undamped oscillations. Since reaching its maximum value the velocity of a body is equal to zero, one can show that the half-cycles of movement increase based on:

Fig. 3Free longitudinal vibrations warp

Of particular interest is the oscillatory motion under the action of harmonic forces. In our case, the sea. Almost 90 % of the time work of this kind of equipment takes place under these conditions. Let this force changes according to the law $F_0\mathrm{s}\mathrm{i}\mathrm{n}pt$.

The desired behavior of a mechanical system under the action of harmonic force is described by the differential equation:

Given Eq. (5) we get a differential equation with constant coefficients, which is integrated in quadratures:

Fig. 4The graph of the forced longitudinal oscillations of the warp taking into account rough sea. The resonance effect

A particular solution of Eq. (10) we find in the form:

where $A=1-\frac{p^2}{{\omega }_0^2}\left(1+kt\right)$ and $B=\frac{kp}{2{\omega }_0^2}$.

Given that resonance occurs when ${\omega }_0=p$ it is possible to determine the time of passage of the model through the resonance region $t_p=\frac{1}{k}\left(\frac{c_2}{m_{30}{p}^2}-1\right)$.

3. Conclusions

The results of the conducted research were obtained the following results:

1. Built an integrated mathematical model of the system “warp-trawl”.

2. The dynamics of change in the longitudinal component of force in here during the mass change of the trawl due to the capture of the object of fishing. In the end, the amplitude of the longitudinal component is not changed, and its half-life increases according to Eq. (9).

3. Researched important moment of the system “warp-trawl”. Namely, the resonance phenomenon, which occurs as a result of rough sea.