Estimation of damping capacity of rubber vibration isolators under harmonic excitation

1. Introduction

Nowadays the questions of preventing the harmful effects of vibration and impact on machines and construction elements requires special attention. In most cases it is necessary to provide of shock and vibration protection at the design stage and best of all to use rubber-like materials for designing such devices [1-5].

The elastic properties of rubber are characterized by a large difference between bulk and shear moduli (K/G ratio reaches 500-5000), the high elasticity of rubbers allows them to withstand the large elongation without breaking; consequently, the rubber has a greater capacity to store energy per unit volume compared with other materials [3-7]. Along with the immediate elastic deformation rubber exhibit a retarded elastic deformation, viscous flow (creep) and relaxation, so its mechanical properties strongly depend on the time of application of external loads, that is, the mode of deformation [6-8]. If the duration of the force causing a deformation equal to the time of relaxation processes in the rubber, the elastic deformation is fully manifested, and this mode of deformation will correspond to well-defined modulus of rubber. When rate of deforming load application increases modulus of elasticity will be changing, and its magnitude will be larger than elastic modulus for the mode with full implementation of the elastic process, this fact must be taking into account when designing shock and vibration absorber. For the optimal design the rubber antivibration devices it is necessary to know mechanical characteristics of elastomers: bulk modulus of compression, dynamic and static shear modulus, damping properties, energy dissipation factor, relationship between stress and strain accounting viscoelastic properties.

In this paper the vibration absorber operating under uniaxial compression – tenion deformation is considered. In Fig. 1 the scheme of mounting and work of this device are shown: elastomeric absorber in the form of rectangular cylindrical or prism is placed between protected object and vibrating base. Rubber element 1 is rigidly attached to the undeformable plates 2. The aim of this work is to determine the dependence of damping properties of rubber absorber on the viscoelastic behaviour of elastomer, on the forced vibration frequency and natural frequency of the system for the model with one degree of freedom (ODF) under the action of harmonic excitation. Mass of absorber is not taken into account because of its smallness. The damping properties are determined by the ratio of the amplitude of the upper plate and mass forced oscillations to the amplitude of the forcing oscillation of base and lower plate. Such approach allows to appoint the dimentions of antivibration devices at design stage.

Fig. 1Schemes of the installed absorbers: 1 – rubber element of height h, 2 – rigid plates, Δ – static deformation caused by Pz

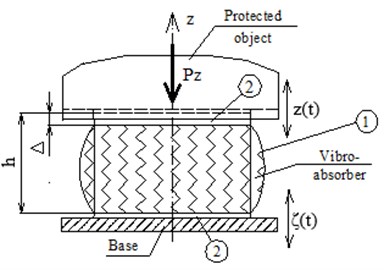
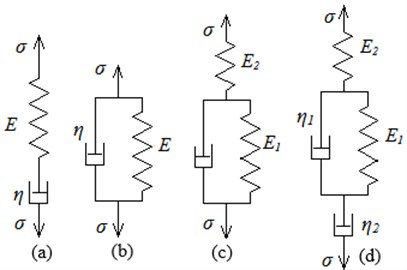
Fig. 2Models of viscoelastic medium: a) Maxwell’s model, b) Voigt model, c) Kelvin’s standard linear medium model, d) Burgers model

2. Simulation versions of viscoelastic properties of rubber

In the mechanical properties of rubber a set of features manifest itself: alongside with the instantaneous elastic deformation these materials exhibit retarding elastic deformation, viscous flow (creep) and relaxation. For clear presentation of the role of elastic and dissipative processes in the mechanical behaviour of materials the mechanical models are used which simplify the understanding of physical meaning of components of a differential equation, describing the relationship between stress and strain in time. It is assumed that for the most materials this equation is linear, and all features of mechanical behaviour may be described by system combining of two basic types of mechanical elements: elastic and viscous [8]. The elastic element is controlled by Hooke’s law $\sigma =E\epsilon$, viscous element – by Newton’s law of flow $\sigma =\eta d\epsilon /dt$. In the elastic element stresses changing is accompanied by an instantaneous directly proportional deformation changing. At constant stress the elastic element is in equilibrium state. The viscous element, in contrast, at constant stress is in a steady flow (at a constant strain rate). Two main elements may be connected together in series or in parallel joint forming two historically the first models of viscoelastic medium: Maxwell’s model (Fig. 2(a)) and Voigt model (Fig. 2(b)), which approximately describe the visco-elastic behaviour of the material. Stress – strain relationship for unilateral deformation are: for Voigt model: $\sigma =E\epsilon +\eta \dot{\epsilon }$, for Maxwell’s model:

where $\sigma$ – normal stress, $\epsilon$ – relative deformation. $E$ – Young’s modulus, $\eta$ – viscosity factor, $\tau =\eta /E$ – relaxation time, which is necessary to establish a new equilibrium state of the material.

Both models have the certain disadvantages, using only them it is impossible to describe all aspects of the mechanical behavior of rubber-like materials. Thus, the Maxwell’s model allows instantaneous elastic deformation and stress relaxation, but does not simulate the equilibrium state of the material under load. Voigt’s model takes into account the retarded elastic deformation, but does not allow deformation jumps and stress relaxation. For adequate describing all features of the mechanical behavior of rubber-like materials it is necessary to complicate the model by increasing the number of elements used. There are four possible schemes of three-elements models and eight schemes of four-elements models. No one of these models is universal, since each of them has its limits of application. The example of three-elements Kelvin’s model, or standard linear medium model, is given in Fig. 2(c), example of four-elements Burgers model – in Fig. 2(d). The relationships $\sigma \left(t\right)–\epsilon \left(t\right)$ for Kelvin’s and Burgers model under unilateral deformation:

The blocks of elements may be, in turn, joined in series. Increasing number of elements (more than four) does not lead to a qualitative refinement time picture of stress – strain.

The most common relationship between stress and strain may be expressed by means of integral equations of relaxation and creep. In this case accounting of the time factor influence is reduced to solving systems of integro-differential equations. Methods of solving such systems are very diverse, the most widely used methods based on the use of integral transforms, especially Laplace and Fourier transforms, and also integral operators of Volterra’s type [5, 8]. In the case of axial deformation for weakly filled rubbers and small deformation ($\epsilon \le$ 20 %), when the linear dependence between stress and strain exists, the dependence is valid: $\sigma \left(t\right)=E_t\epsilon \left(t\right)$, where $E_t$– time operator, not depended on $\sigma$ and $\epsilon$ and reflects the viscoelastic behaviour of system.

This dependence may be written in the form of an integral equation of Volterra:

where: $E_0$ – instantaneous compressive modulus, which specifies the instantaneous stiffness in the classical sense; $R\left(t-\tau \right)$ – relaxation kernel describing the viscoelastic properties of the rubber. Using Fourier – images transform of $\sigma \left(\omega \right)$, $\epsilon \left(\omega \right)$ and $R\left(\omega \right)$ Eq. (3) may be written as:

where $E\left(\omega \right)$ – dynamic compression modulus of elasticity expressed as complex modulis.

Proposed by A. Rzhanitsin, Y. Rabotnov and M. Koltunov kernels are in most common use. These kernels allow satisfactory describing mechanical properties of rubber in medium frequency range 10^-3 $<\omega <$10³ s^-1. In this work Rabotnov’s kernel is considered, which represents fractional exponential function $R\left(t–\tau \right)={Э}_{\alpha }\left(–\beta ,t–\tau \right)$. Rabotnov’s kernel and its Fourier image:

where 1 $<\alpha <$ 0, $\beta >$0, $\alpha$ – parameter of fractionality, expressed in terms of the maximum value of the spectrum of relaxation times and modulus defect, $\beta$ – rheological characteristics of rubber, $\mathrm{\Gamma }$ – gamma-function. Parameters $\alpha$ and $\beta$ are in detail tabulated for many types rubbers.

Taking into account Eqs. (4) real and imaginary parts we obtain from Eq. (5):

The coefficients $B_1$ and $B_2$ are Fourier cosine and sinus transform of the function $R\left(t–\tau \right)$. The elastic modulus dependence on frequency should be considered as the conditional characteristics, as they are not applicable to any of a periodic process with a known frequency, but only to monochromatic described by harmonic functions $\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$, $\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$, $\mathrm{e}\mathrm{x}\mathrm{p}\left(i\omega t\right)$.

3. Models of damping system with one degree of freedom

The dynamic properties of rubber absorber it is possible to estimate most clearly in the frame of the simplified one-degree-of-freedom model (Fig. 1), which allows to obtain explicit analytical dependences for damping characteristics. Protected object is represented as a point mass, vibration isolator is placed between protected object and vibrating base with kinematic excitation in accordance with time dependence of $\zeta \left(t\right)$. The time dependence of the protected object motion is $z\left(t\right)$. Since $\zeta$ and $z$ are defined in the inertial system, the relative motion of the object and base will be equal to $z\left(t\right)-\zeta \left(t\right)$, and deformation of the elastomer layers thickness $h$ is equal to:

Let function $\zeta \left(t\right)$ is periodic with amplitude ${\zeta }_0:\zeta ={\zeta }_0\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$. Since the system is linear, for the harmonic input function all caused output processes will also be harmonic functions with the same frequency but with phase delay. Then it is natural to assume that function $z\left(t\right)$ will be as follow: $z=z_0\mathrm{c}\mathrm{o}\mathrm{s}(\omega t+\phi )$, where $z_0$ – amplitude of steady-state vibrations of mass, $\phi$ – angle of lag. The force imposed on the object with mass $m$ from the elastic support is equal $F=A\sigma \left(t\right)$, where $A$ – area of the upper face of the antivibration device.

The equation of motion of mass $m$ in $z$ – direction is:

For Maxwell’s model the equation of mass $m$ motion is received accounting Eqs. (1, 7, 8) and denoting natural frequency of mass vibration ${\omega }_0=\sqrt{AE/mh}$:

For harmonic deformation taking into account linear independency of the functions $\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$ and $\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$, the system of the equations is obtained from Eq. (9):

Received from system Eq. (10) forced and forcing vibration amplitudes ratio $z_0/{\zeta }_0$ and lag angle $\phi$:

For Burgers model taking into account Eqs. (2, 7, 8) and denoting ${\omega }_0=\sqrt{A{E}_2/mh}$ (since $E_2$ is accounted initial modulus) equation of motion, amplitudes ratio $z_0/{\zeta }_0$and lag angle $\phi$ are received:

Mass motion equation depending on the viscoelastic properties of the rubber is received taking into account Eqs. (3, 8):

Denoting the natural frequency of vibrating mass as ${\omega }_0$ and taking into account Eq. (7), the equation of object motion is received in the form:

Using the property $R\left(t-\tau \right)=$ 0 if $t<\tau$, for harmonic deformation the system of the equations is obtained from Eq. (15):

From system Eq. (16) the amplitudes ratio or of the forced vibration amplitude of mass $z_0\left(\omega \right)$ and the angle of lag $\phi \left(\omega \right)$ may be found:

By the same way parameters of shear vibration may be determined.

4. Numerical examples

The results of calculation of damping properties of rubber vibroisolator in accordance with above described algorithms and equations are given below. Numerical examples was solved with help of Mathcad-15 program. The curves of ratio $z_0/{\zeta }_0$ dependence functions on $\omega$, as well as $\phi$ on $\omega$ functions are constructed according to Eqs. (11-13, 17, 18); in all cases solution was fulfilled for five natural frequencies ${\omega }_0=$ 1, 5, 10, 15 and 20 s^-1.

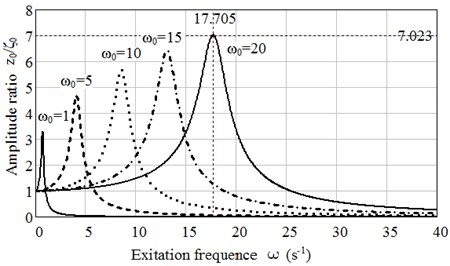
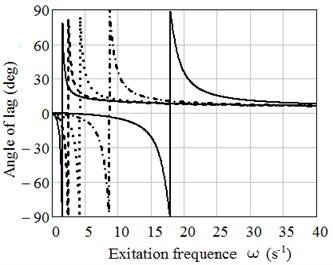
Solution based on Rabotnov’s kernel is presented in Fig. 3, where plots of dependence the amplitudes ratio (a) and angle of lag (b) on excitation frequency are given for low-filled rubber 2959. Rheological parameters of this rubber $\alpha =$ –0.6 and factor $\beta =$1.062 [6].

In Fig. 4(a) plots of dependence of the amplitudes ratio $z_0/{\zeta }_0$ on excitation frequency $\omega$ calculated in accordance with Maxwell model, in Fig. 4(b) in accordance with Burgers model are presented.

In both cases calculations were performed for rubber 8157. Maxwell model parameters $E=$ 2.55 MPa, $\eta =$ 1.04 MNs/m² and Burgers model parameters $E_1=$ 8.93 MPa, $E_2=$ 3.58 MPa and ${\eta }_1=$ 0.057 MNs/m², ${\eta }_2=$ 1.04 MNs/m² were taken from [5].

It is seen from the plots that simple Maxwell model describes the behaviour of rubber absorber inaccurately, but it may be used in a first approximation.

Fig. 3Plots of dependence of a) amplitude ratio z0/ζ0 on excitation frequency ω and b) the lag angle φ on excitation frequency ω, calculated based on Rabotnov’s kernel for ω0= 1, 5, 10,15 and 20 s-1

a)

b)

Fig. 4Plots of dependence of a) amplitude ratio z0/ζ0 on excitation frequency ω calculated with accordance to Maxwell mode, b) calculated in accordance to Burgers model for ω0= 1, 5, 10,15 and 20 s-1

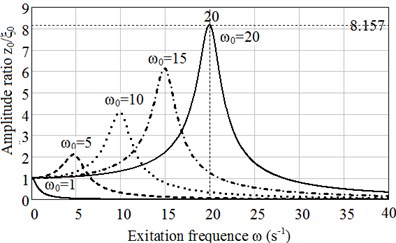
a)

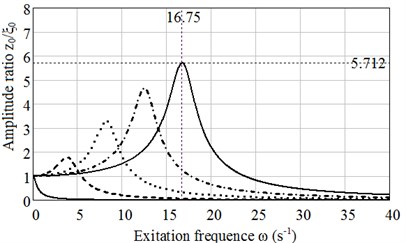
b)

5. Conclusions

This paper presents the procedure of estimation of damping properties of rubber absorber for ODF system under harmonic excitation. Definition of damping properties is fulfilled for system with kinematic excitation based on two approaches: using Maxwell and Burgers mechanical models combining of elastic and viscous elements and using Rabotnov’s kernel of relaxation for analytical representation of viscoelastic properties of rubber. Damping properties are expressed by the ratio of the amplitude of the driving lower base to the amplitude of the forced oscillations of the upper base and the object. Rubber absorbers of rectangular prismatic form, compressed in the normal to flat surface direction, is calculated as the examples.

Symbolic and numerical computations was fulfilled on Mathcad-15 program. Calculations confirm the well-known fact from the theory of vibration protection: if natural frequency of the object is three times lower than frequency of the forcing oscillations, the forced oscillation amplitude is attenuated approximately in ten times. Such vibration isolators show good results on above resonance frequencies. It may be concluded that proposed approach is suitable for dimensioning of rubber absorber on design stage.

Form factor accounting, i.e. shape influence on object natural frequency and experimental study of damping properties of rubber vibroisolator will be the next step of current research work.