A fractional Maxwell approach for the shock response of viscoelastic oscillator

1. Introduction

Heavy-duty engineering vehicles, aeronautics and astronautics are often subjected to shock vibration with time-varying frequency and amplitude, inducing system equipment damage or failure. Viscoelastic damping structures are mounted on above systems to control vibration and noise by converting mechanical energy into heat consumption. The heat consumption is generated from internal friction, induced by hysteretic damping of viscoelastic materials. It is very common that viscoelastic engineering bears the shock loading with high amplitude and short duration. The strain rate of viscoelastic material under shock loading is about six or seven orders of magnitude higher than that of conventional quasi-static experiment. Under shock loading with variable amplitude and frequency, the damping structures are always in a multifactorial dynamic state, of which the dynamic responses are obviously different from that under low strain rates. A large number of studies on viscoelastic behavior of materials under low strain rate are mainly based on static load, quasi-static load and harmonic excitation experiments. The dissipation performance of damping structures based on above analyses could not well match to system parameters. Therefore, it is essential that the viscoelastic material characteristics at high train rate could be accurately and reliably described for the shock response analysis of viscoelastic damping structures.

The hysteresis properties of viscoelastic stress-strain relationship have attracted great attention of many researchers. Previous studies focus on the mechanical properties of viscoelastic material at low strain rates [1, 2]. These models may be divided into following several kinds of standard rheological model, complex modulus model, mini-oscillator model, fractional derivative model and fractional exponential model. The Maxwell, Kelvin-Voigt, standard linear solid, Bürgers and Zener models are the traditional and typical models. More recently, some viscoelastic constitutive model based new theories and methods are proposed. Xu Mingyu et al. [3] proposed a viscoelastic model based on new generalized fractional element networks, which should extend the model solutions to the generalized function space by adding the coordination equation and introducing the inverse Laplace transform using discrete data. Mulianaa A. et al. [4] formulated a nonlinear viscoelastic constitutive model based on multiple natural configurations and a single integral constitutive representation, which incorporated the effect of microstructural changes on the macroscopic deformations of polymers. Fractional viscoelastic models with non-singular kernels and the different performance of the models defined by different fractional derivative were investigated [5]. A fuzzy fractional K-V model considering the uncertainty in variables and the numerical algorithm using a spectral tau technique were presented [6]. Alotta G. et al. [7] came up with three-dimensional isotropic fractional viscoelastic model to simulate the viscoelastic behavior of complex components, and also proved that the model can satisfy the correspondence principles for the viscoelastic Poisson’s ratio.

The low-rate response of viscoelastic damping materials has been adequately studied, while a few researches focus on the shock response. The shock response can only be obtained by high strain rate experiments, but not by conventional quasi-static experiments. The split Hopkinson pressure bar (SHPB), invented by Kolsky in 1949, is a classical device to quantify the constitutive behavior of various materials at high strain rates [8-11]. The impedance and wave velocity of viscoelastic damping material is so small that some difficulties during the traditional SHPB test are encountered. On the one hand, the transmission signal is too weak to reach a better signal-to-noise ratio. On the other hand, it’s difficult to ensure the homogeneous deformation and stress equilibrium during the SHPB experiment. Meenken T et al. [12] presented a modified SHPB for testing low impedance materials and investigated large deformations of EPDM and PU rubber sample. Zhao Xijin et al. [13] investigated the dynamic compressive behaviors of a silicon rubber at high strain rates by applying quartz crystal. Lee O. S. et al. [14] analyzed the dynamic deformation of rubber by using the SHPB technique, and found that the relationships between the stresses and the strain rates at the transition point are found to be bilinear. Doman D. A. et al. [15] performed the high-rate, uniaxial compression tests using a Polymeric SHPB, and studied the effectiveness of both the modified quasi-linear viscoelastic model and the non-linear hyper-viscoelastic model to describe the low-rate and high-rate behavior of polyurethane rubber. Zhu Zhaoxiang et al. [16] proposed the ZWT nonlinear viscoelastic constitutive model, and then analyzed the strain rate effect and the time-temperature equivalence relation on mechanical properties of epoxy resin. Zhou Haixia et al. [17] performed the low, intermediate and high strain rate compressive testing and employed ZWT model to study the compressive mechanical behaviors of the propellant. It was proved that four Maxwell elements at least in the model should be required to accurately describe rate-dependent mechanical properties. By applying characteristics method of wave propagation, Zhu Jue et al. [18] numerically studied the SHPB tests for the so-called ZWT viscoelastic materials to explore how the basic assumption of uniform distribution of stress can be satisfied. L. M. Yang et al. [19] presented a visco-hyperelastic constitutive model to analyze the large-deformation response of incompressible rubber under high strain rates, which should characterize the static hyperelastic behavior, rate-sensitivity and strain history dependence. By replace Rivlin function with Yeoh function in the constitutive model, Zhou Xiangrong et al. [20] proposed a new nonlinear constitutive based on Yeoh strain energy function to describe intermediate and high strain rate effects of rubber.

Studies have shown that viscoelastic damping material has not only the elastic and viscous coexisting characters, but also the obvious historical dependence. The integer order model has many parameters and unclear physical meaning, which could not reflect the historical correlation of materials. Other studies have been proved that four integer Maxwell elements at least with many unclear physical meaning parameters are required to accurately describe the rate-dependent mechanical properties of viscoelastic materials. However, the fractional calculus could well represent the historical correlation of the system due to its global definition [21]. The fractional model has fewer parameters and clear physical meaning, which has been proved a powerful model to simulate the dynamic properties of viscoelastic damping material.

In conclusion, yet few of researches have investigated the shock behavior of viscoelastic materials with the fractional constitutive model. In this paper, the fractional Maxwell model (FMM) is presented based on the fractional constitutive model and the typical Maxwell model. The compressive experiments can be conducted on the aluminum SHPB system to verify the adopted model. Besides, the experimental stress-strain curves of materials are explained based on the damping dissipation mechanism. Afterwards, a set of model parameters are obtained by the least-squares fitting algorithm. Finally, the comparison is made between FMM model and the other models including the fractional Kelvin-Voight model, ZWT model and Ogden model considering the strain rate-dependent.

2. Fractional Maxwell constitutive model

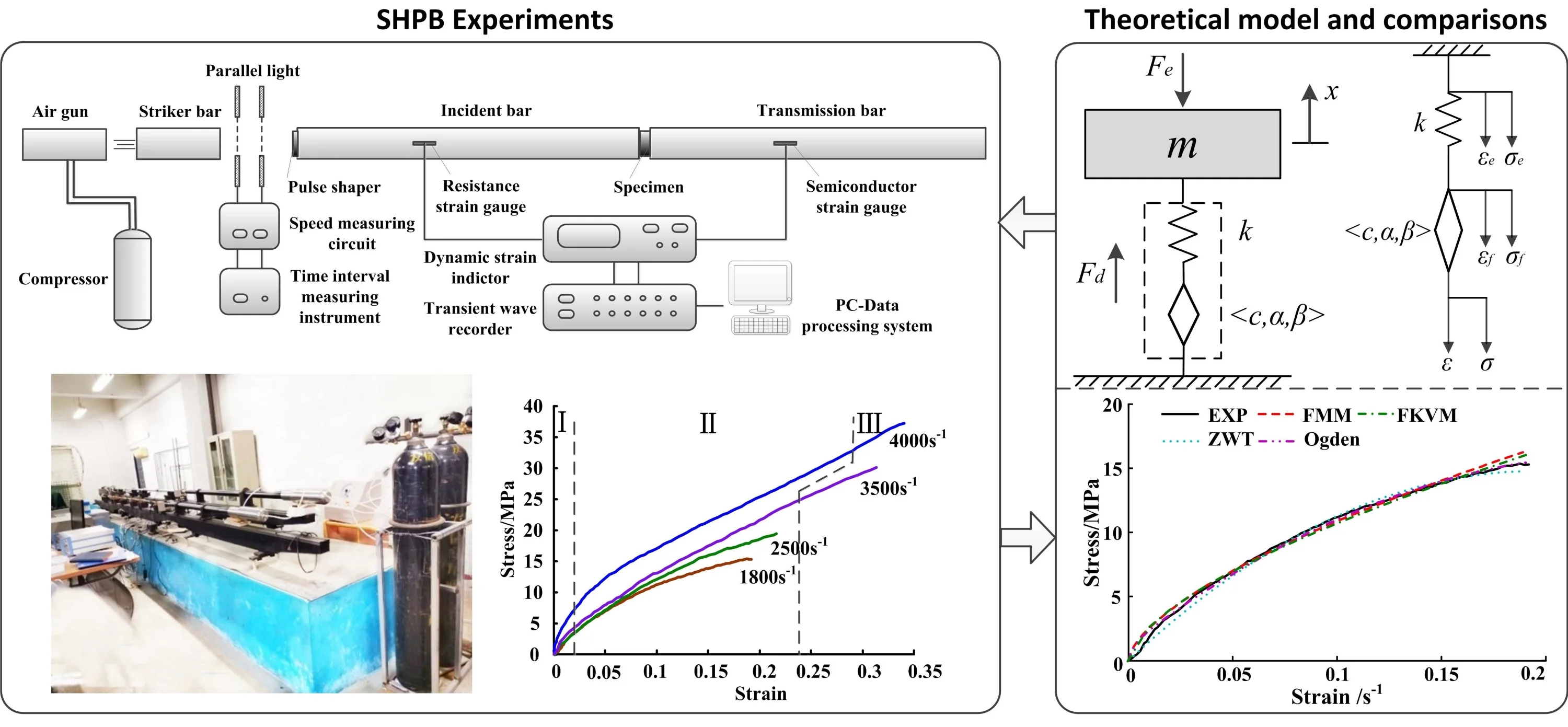
The viscoelastic oscillator (VEO) is the fundamental physical unit of viscoelastic damping structures. The VEO depicted in Fig. 1(a) consists of an isolated mass, viewed as $m$ whose displacement is represented by $x$, a viscoelastic isolator with the specific geometric elements namely the area $A$ and the height $l$, and the external excitation $F_e$. The viscoelastic isolator is installed on the rigid support.

The fractional constitutive equation including the strain $\epsilon$ and the stress $\sigma$ for viscoelasticity takes the following form [22]:

where the fractional constitutive operators $P$ and $Q$ are respectively defined by:

where $p_i$ and $q_i$ are coefficients, $D_t^{{\alpha }_i}$ and $D_t^{{\beta }_i}$ are fractional derivative operators whose Caputo definitions are respectively defined by:

where ${\alpha }_i$, ${\beta }_i$ are the fractional orders, $n=\left[{\alpha }_i\right]$, $\left[{\beta }_i\right]$, $n-1<{\alpha }_i$, ${\beta }_i\le n$.

The FMM model is employed to characterize the viscoelastic stress-strain relationship, which consists of the fractional dashpot $〈c,\alpha ,\beta 〉$ in series with the ideal Hooke spring element $k$, shown in Fig. 1(b). Compared with the original Maxwell model, the integer order sticky strain element is replaced by the fractional dashpot in the FMM model. According to the FMM model, the relations ${\sigma }_e={\sigma }_e={\sigma }_f$, $\epsilon ={\epsilon }_e+{\epsilon }_f$ are established, where ${\sigma }_e$, ${\epsilon }_e$ are the stress and strain of the spring element, and ${\sigma }_f$, ${\epsilon }_f$ are the stress and strain of the fractional dashpot, respectively. Based on the above models, the VEO concluding FMM shown in Fig. 1(c) is built. The comprehensive function of the viscoelastic isolator counts as a fractional damping force $F_d$. Herein, $F_d=\sigma A={\sigma }_{e}A={\sigma }_{f}A$. In the FMM model, the parameters of viscoelasticity are as follows. $n=$1, $p_0=$1, $p_1=c/k$, ${\beta }_0=$0, ${\beta }_1=\beta$, $m=$1, $q_0=$0, $q_1=c$, ${\alpha }_1=\alpha$. Therefore, the fractional Maxwell constitutive equation including the strain $\epsilon$ and the stress $\sigma$ for viscoelasticity is derived:

Fig. 1VEO and FMM models

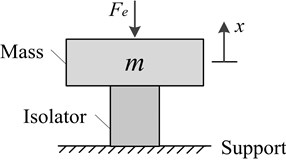
a) Physical model of VEO

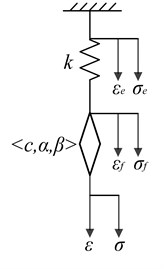
b) FMM model

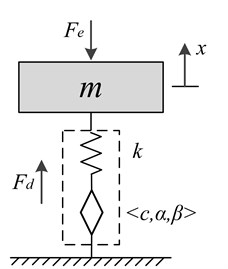
c) VEO concluding FMM

3. SHPB experiment

3.1. Experimental scheme

As an essential experiment of the shock dynamic properties, the compression experiment could undergo large deformation without necking, which is different from the conventional quasi-static tensile experiment. Using the wave propagation principle, the experiment in this paper is conducted on the aluminum alloy separated Hopkinson pressure bar (SHPB) with low impedance. The SHPB system is mainly composed of the striker bar, the incident bar and the transmission bar with the same diameters of 14.5 mm, mass density 2.8×10³ kg/m³, Young’s modulus 72 GPa and longitudinal wave velocity 4982 m/s, and the different lengths (0.60 m, 2.00 m and 2.00 m, respectively). The specimen is located between the incident and transmission bars. By the gas from the air gun, the strike bar is propelled forward against the incident bar, generating compression stress waves. When the waves are transmitted to the specimen, a part of the waves is reflected as tensile wave back to the incident bar, while the other portion is transmitted to the transmission bar. The above pulse signals are recorded by the strain gauges located on the incident bar and the transmission bar respectively. The real photos and the schematic of the SHPB test machine are shown in Figs. 2-3, respectively.

Based on the one-dimensional stress wave assumption, the strain rate, strain and stress could be calculated by:

6

$\dot{\epsilon }=\frac{C_0}{L_S}\left[{\epsilon }_i\left(t\right)-{\epsilon }_r\left(t\right)-{\epsilon }_t\left(t\right)\right],$

7

$\epsilon =\frac{C_0}{L_S}{\int }_0^t\left[{\epsilon }_i\right(t)-{\epsilon }_r(t)-{\epsilon }_t(t\left)\right]dt,$

8

$\sigma =\frac{A_0}{2A_S}{E}_0\left[{\epsilon }_i\left(t\right)+{\epsilon }_r\left(t\right)+{\epsilon }_t\left(t\right)\right],$

where ${\epsilon }_i\left(t\right)$, ${\epsilon }_r\left(t\right)$ and ${\epsilon }_t\left(t\right)$ are the incident, reflected and transmitted strain propagating within Hopkinson pressure bars, respectively. The parameters $A_0$, $E_0$, and $c_0$ are the cross-sectional area, the Young’s modulus and the elastic wave velocity of the bars. The parameters $A_s$ and $L_s$ are the cross-section area and the thickness of the specimen.

Fig. 2The photos of the SHPB test system

a) SHPB experimental facilities

b) Data processing devices

Fig. 3The schematic of the SHPB test system

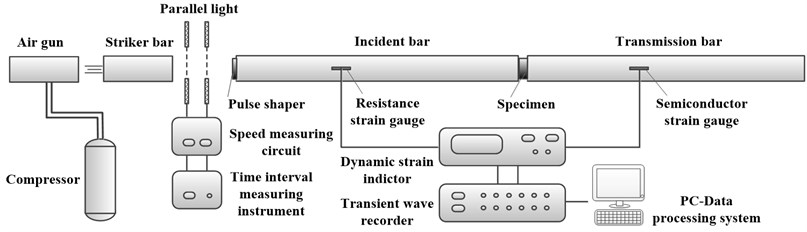
The natural rubber with hardness 70 HS is chosen as the experimental material. Considering viscoelastic damping material with low impedance and low wave velocity, the specimen of small thickness is chosen in order to shorten the time of stress wave propagation and achieve the stress equilibrium. On the other hand, the optimal length-diameter ratio of the specimen is $h/r=\sqrt{3}/2$ [23]. Thus, the specimen is designed to be a short cylindrical with 6.5 mm in diameter and 2 mm in length. To reduce the influence of the interfacial friction between the specimen and the bar ends, a thin layer of petroleum jelly are used to lubricate the two contact surfaces of the specimen. The incident bar is instrumented with the resistor strain gauges of sensitivity coefficient 2.1±1 %, while the semiconductor strain gauges of sensitivity coefficient 110±5 % are associated on the transmission bar for capturing the weak transmitted pulse.

During the SHPB experiment, it is vital to obtain the dynamic stress equilibrium and constant strain rate. In the traditional SHPB experiment of soft materials, the above conditions are difficult to be guaranteed, so that the experimental results cannot truly reflect the material properties. To achieve desired experimental results, the most widely applied approach is the technique of placing pulse shapers between the strike bar and the incident bar. The reason is that the plastic deformation of the shapers during the loading process could change the shape of pulse. Some achievements about pulse shapers have been made based on the dynamic experiments of the soft material. To study rubber materials, Pang Baojun et al. [24] used a lead block with a side 3 mm to adjust the pulse. Chen [25] employed the polymer wafer as the incident-pulse shaper to test the dynamic compressive response of polymeric nanocomposites. Chang Xinlong [26] studied the constitutive model for HTPB propellant using the rubber wafer as the pulse shaper. Lu Fangyun [27] performed the SHPB experiments of silicone rubber and foam materials by applying the combination pulse shaper of a main shaper, a very small copper shaper and even a smaller silicone rubber shaper. Wang Baozhen [28] studied the constitutive model of porcine liver by means of the shaping technique of multi-layer medical plaster. In this paper, considering viscoelastic materials with low stiffness, the multi-layer adhesive plaster of 1 mm thickness is employed to shape the incident pulse. The comparison between strain curves before and after the shaping technology is illustrated in Fig. 4. It should be seen that the shaper of multi-layer adhesive plaster could eliminate the high frequency shock introduced by the dispersion effect, and thus help the specimen to early achieve and maintain the uniform stress and constant strain rate.

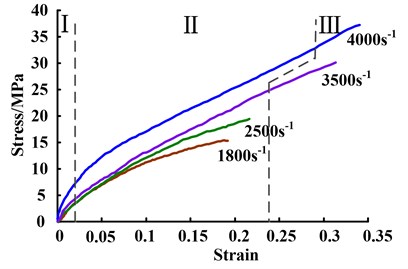
To study the shock response of viscoelastic damping material, SHPB experiments are conducted for four different strain rates (1800 s^-1, 2500 s^-1, 3500 s^-1 and 4000 s^-1). The experimental stress-strain curves are presented in Fig. 5.

Fig. 4The comparison between strain curves before and after the shaping technology

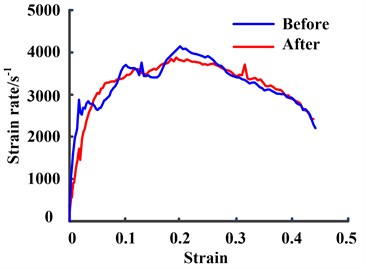
Fig. 5The experimental stress-strain curves of viscoelastic damping material

4. Comparison study

The parameters of FMM are obtained by least-squares fitting against the SHPB experiment data as $c=$2.7×10⁶ N·s/mm, $k=$ 4.5×10⁷ N/mm, $\beta =$0.101, $\alpha =$0.381, 0.384, 0.387, 0.395, corresponding strain rate 1800 s^-1, 2500 s^-1, 3500 s^-1and 4000 s^-1, respectively. The mechanical behavior of viscoelastic damping material under different strain rates could be embodied by the fractional order of the FMM model, which could not be reflected by the classical viscoelastic model. For purpose of comparing study, the fractional Kelvin-Voight model (FKVM), ZWT model and Ogden model considering the strain rate-dependent are also applied to predict the shock stress-strain curves of viscoelastic damping material by SHPB.

The constitutive equation of FKVM model [30] is:

where, $q_0=k$, $q_1=c$ are material parameters.

The constitutive equation of ZWT [16] model is:

where, $C_0$, $\alpha$, $\beta$ are the elastic constants of nonlinear elements, $C_1$, ${\theta }_1$ and $C_2$, ${\theta }_2$ are elastic constants and relaxation times of the two Maxwell elements, respectively.

Considering the influence of the strain rate, the engineering stress of Ogden model for rubber materials under uniaxial compression condition is expressed as [31]:

where, ${\lambda }_1$ is the principal stretch, ${\lambda }_1=1-\epsilon$ and ${\dot{\lambda }}_1=\dot{\epsilon }$. ${\alpha }_j$, ${\mu }_j$, and $G_i$, ${\beta }_i$ are material parameters.

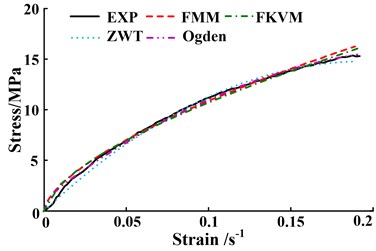
The fitting results are shown in Fig. 6. The root mean square error (RMSE) is also implemented to measure the fitting quality between the experimental data and theoretical models. The definition of RMSE is:

where, $y_t$, $y_e$ are the experimental data and the theoretical value, respectively. The RMSE of the different model-fitting data at each strain rate is represented in Table 1.

Fig. 6The comparisons between predicted models and experimental data at different strain rates

a) Strain rate 1800 s^-1

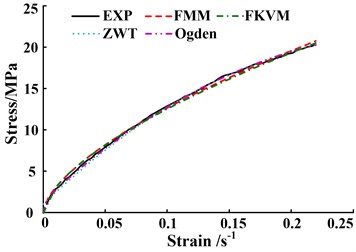
b) Strain rate 2500 s^-1

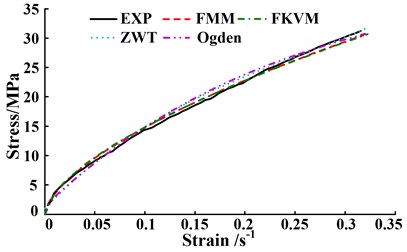
c) Strain rate 3500 s^-1

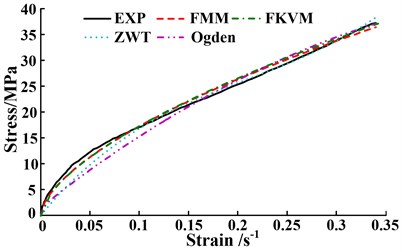
d) Strain rate 4000 s^-1

The comparisons illustrated in Figs. 6(a)-(b) and Table 1 show that at strain rates 1800 s^-1 and 2500 s^-1, the Ogden model has the highest fitting accuracy to experimental data, closely followed by the ZWT and FMM models, and the FKVM is the worst. The difference of the fitting accuracy between the FMM model and the Ogden model is very small, and the RMSE differences between them are 0.067 and 0.057, respectively. The RMSE differences between the FKVM model and the Ogden model are 0.167 and 0.423, respectively. Additionally, the high-precision fitting of the Ogden and ZWT models at strain rates 1800 s^-1and 2500 s^-1 may be built on the complex fitting of multiple parameters with ambiguous physical meaning. The fitting of the parameters also require longer convergence time. There are two relaxation times varying within their range in the ZWT model, which increase the flexibility and uncertainty of fitting process.

At strain rates 3500 s^-1and 4000 s^-1, the FMM and FKVM models perform much better agreement with experimental data than the ZWT and Ogden models, shown in Figs. 6(c)-(d) and Table 1. Especially at strain rate 4000 s^-1, the ZWT and Ogden models significantly deviate from experimental values in small strain region, of whose RMSEs are larger one order than that of FMM model.

The mean of RMSE for above models is 0.460, 0.578, 0.762 and 1.076, respectively. As a fractional-order model, FMM model has the minimum mean of RMSE among the four models. Besides, the FMM model just has four parameters. More importantly, the fractional orders of the FMM model could reflect the elastic and viscous distribution of materials under different strain rates. The FMM model has a better comprehensive superiority in the characterization of viscoelastic shock mechanical behavior. The superiority is embodied at higher fitting precision, fewer parameters and clear physical meaning.

5. Conclusions

In this study, the FMM model is presented for the shock response of viscoelastic damping material. The dynamic experiments for four strain rates (1800 s^-1, 2500 s^-1, 3500 s^-1 and 4000 s^-1) are performed by SHPB system to examine the proposed model. Meanwhile, the models of FMM, fractional Kelvin-Voight, ZWT and Ogden considering the strain rate-dependent are comparatively studied with the experiment. The conclusions could be summarized as follows.

1) The stress-strain curves at high strain rates should be divided into three stages, i.e. the linear stage, the strain-softening stage and the strain-hardening stage. The strain rate effect could be observed. With the strain rate increasing, the peak strain, the peak stress and the curvature of the curve in strain-softening stage increase, and the hardening effect in the strain-hardening stage presents increasing tendency. It is because the action time of external loading gets closer to the relaxation time of the molecular chain segment with increase of the strain rate, thus leading to the apparent strain rate-dependence of molecular slip and friction.

2) At strain rates 1800 s^-1and 2500 s^-1, the Ogden model has the highest fitting accuracy to experimental data. The difference of the fitting accuracy between the FMM model and the Ogden model is very small, and the RMSE differences between them are 0.067 and 0.057, respectively. At strain rates 3500 s^-1and 4000 s^-1, the FMM and FKVM models perform much better agreement with experimental data than ZWT and Ogden models. Additionally, as a fractional-order model, FMM model has the minimum mean of RMSE 0.460 among the four models.

3) In general, the FMM model has a comprehensive superiority of higher fitting precision, fewer parameters and clear physical meaning to describe the shock mechanical behavior characteristics of viscoelastic materials in a wider range of strain rate.