Diagnostics of bearings in hoisting machine by cyclostationary analysis

1. Introduction

The topic of damage diagnostics in rotating machinery has been widely studied in the literature [1-2]. Many different methods have already been introduced and applied to real data. One of the most popular approaches are based on the principle of selecting frequency bands containing the most information about a local fault, e.g. spectral kurtosis, protrugram and other [3-5]. Furthermore, in [6] the application of alpha-stable distribution for selection of informative frequency band is proposed. Intuitively, the impulses generated by the local fault in the rotating machinery are cyclic. Moreover, once the rotational speed is constant their period does not vary significantly. Thus, such signal can be treated as a cyclostationary of order two. Cyclic power spectrum has been shown as a powerful tool for damage detection in the rotating machines [7]. One of the biggest problem of the cyclostationary approach is the computational complexity of the algorithm. In most of the cases the methods are significantly slower than the standard one which may, e.g. impact their effective use in online applications. Thus, in many scientific papers many new and faster alternative algorithms are proposed. In [8] the new envelope-based algorithm for cyclic periodogram is suggested. It is shown in [9] that the sliding discrete Fourier transform can be applied in order to speed up cyclic modulation spectrum calculation. Another widely used cyclostationary method is spectral coherence (SC) [10]. This method indicates for which modulation frequency the cyclic impulses can be observed in the signal. This text shows the results of applying SC on the vibration signal recorded from a hoisting machine located in the underground mine. The presented signal is of a complex structure and consists of many different components. Hence, the damage detection is a challenging problem.

The paper is organized as follows. In Section 2 the description of the experiment is provided. The application of the SC to real data is illustrated in Section 3. The conclusions of the work are presented in Section 4.

2. Description of hoisting machine and data acquisition conditions

Hoisting machine is build-up in vertical shaft and is tower mounted multiple rope friction type. Shaft consists of two compartments. Device is equipped with head ropes and tail ropes of the same weight per unit length, thus the only out of balance load is simply the payload. Hoist is powered by two electric motors build on one shaft and equipped with two bearings of the same size which supports the shaft loads. Machine is used to haul ore from underground to the surface. The vibration signals were collected from a rolling element bearing operating on a hoisting machine. Data from a number of accelerometers were recorded simultaneously by a dedicated ABB system at the rate of 51.2 kS/s. The signals were collected during a time window in which the machine was operating with a constant operational speed of 70 RPM.

3. Real data analysis

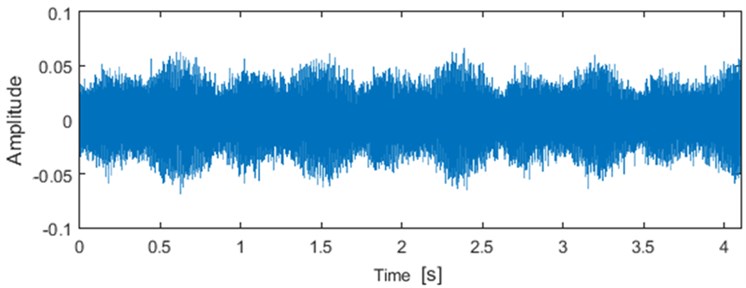
The vibration signal measured on the machine depends on the speed, the load and the location of the measurement. One can easily distinguish between the phases of run-up, constant speed and cost-down. Moreover, in Fig. 1 the operating cycle are clearly visible and can be separated from a stoppage phase due to much higher vibration amplitudes. To simplify the analysis on the current stage of the research, in order to perform the damage detection in the machine it is beneficial to analyze only the signal during the nominal speed. Thus, it is enough to use signal of length 4 seconds (Fig. 2).

Fig. 1The long signal recorded on the hoisting machine. Red box marks one operating cycle

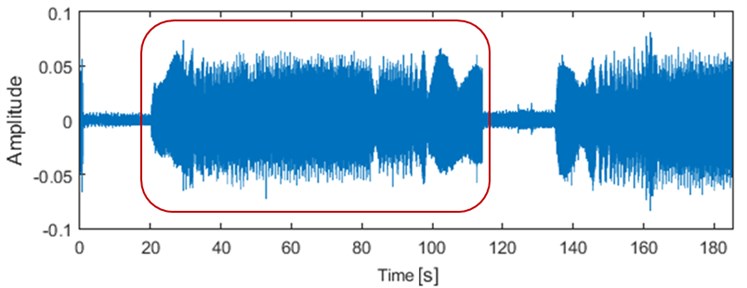
Fig. 2The short signal recorded on the hoisting machine

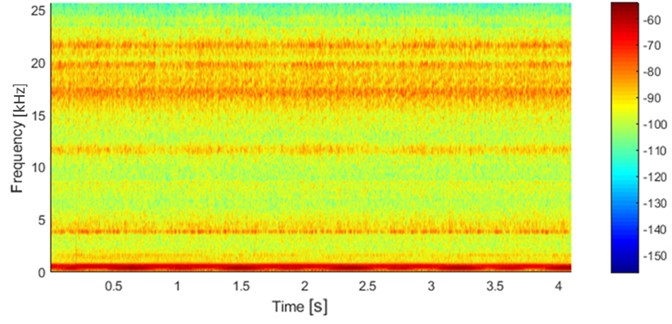
The signal is recorded prior to suspected inner race damage, and so the focus is on extracting information related to this fault frequency from the signal. Firstly, the signal is presented in the time-frequency domain, by means of a spectrogram (Fig. 3). One can observe that the highest energy concentrates mostly in the regions around the low frequencies (0-1 kHz). Furthermore, high energy is also detected for frequencies around 4 kHz, 13 kHz and in the wideband 17 kHz-23 kHz. On the other hand, it is hard to detect any fault from the spectrogram.

Fig. 3Spectrogram from the short signal (from Fig. 2) with Kaiser window length 256 and overlap 92 %

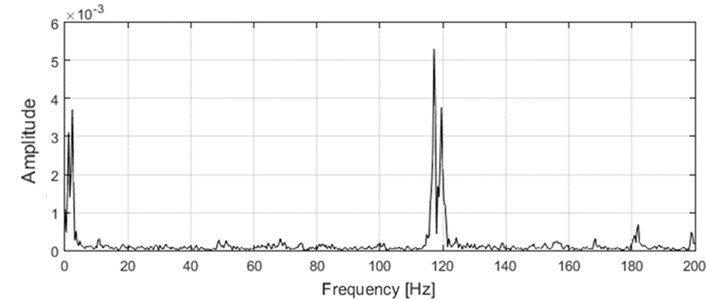
One of the most fundamental tool for localized fault detection is undoubtedly the envelope spectrum. The presence of localized fault should lead to generation of harmonics of characteristic fault frequencies. The envelope spectrum from the short signal is presented in Fig. 4 Clearly, the harmonics related to fault frequency 13.57 Hz are not observed. Thus, the classic envelope spectrum fails to provide information about the fault.

Fig. 4Envelope spectrum from the short signal

Cyclostationary methods are one of the most powerful for fault detection in the vibration signal acquired on the rotating machinery. Typically, a local fault results in generation of impulses in the vibration signal. Moreover, these impulses are expected to be periodic, i.e. equally spaced in the signal. It is said, that signal $x\left(t\right)$ is second-order cyclostationary with period $T$ when its mean and autocorrelation are periodic [11]:

where $\mu$ is mean, ${\sigma }^2$ is variance and $T$ is the smallest constant satisfying above equations. The prominent tool for fault detection in cyclostationary signal is spectral coherence, which was introduced in [10]. Firstly, let us introduce the cyclic power spectrum [10]:

where $I_{x,L}\left(f\right)$ is signal $x\left(t\right)$ Fourier transform with $L$ points for frequency $f$. Thus, it measures the dependence between spectral points spaced by frequency $\alpha /2$. It is beneficial to analyze the normalized version of cyclic power spectrum. Thus, the spectral coherence is given by the following formula [10]:

The performance of SC and other bi-frequency maps has been already tested for another mining machines, e.g. crushers, conveyors etc. [11-13]. As indicated earlier, SC provides information about the modulation frequencies for which the excitation can be observed in the signal. Thus, in the presented case the SC should reveal the presence of the excitation at the inner race fault frequency. The SC for analyzed signal is presented in Fig. 5. It is noteworthy that the excitation for modulation frequency around 13.6 Hz is observed. On the other hand, high amplitudes are also obtained for modulation frequencies 10.6 Hz, which is the frequency of the bearing outer race. It is worth mentioning that both excitations are wideband and are observed for almost all frequencies.

Fig. 5Spectral coherence for the short signal

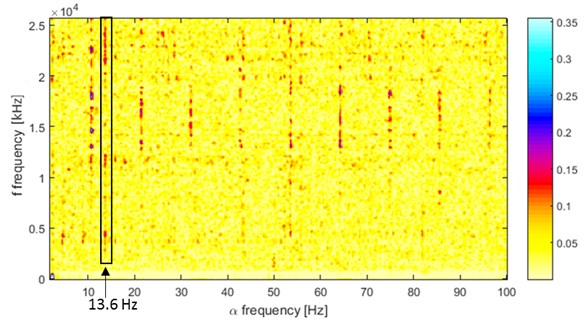
Fig. 6The integrated SC map for the short signal

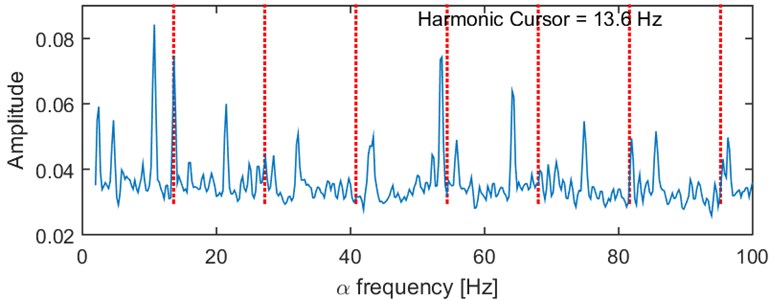
Finally, the mean value from the SC for each modulation frequency can be computed. It indicates the frequencies for which the highest amplitudes can be obtained. The results for hosting machine data are illustrated in Fig. 6. Clearly, the peak for 13.6 Hz is observed. At the same time however not signatures of the multiples of 13.6 Hz can be seen.

It should be mentioned that the problem of hoisting machine vibration signal processing was already investigated by Batko and Mikulski, however this paper aimed to detect damage of the bearing, contrary to signal denoising by wavelet approach presented in [14].

4. Conclusions

This paper describes the fault detection with cyclostationary methods for hoisting machine. The well-known Spectral coherence method was applied to identify the modulation frequencies, for which periodic impulses are present. It is shown that despite the vibration signal being complex and comprising many different components, the presence of characteristic fault frequency can be seen. The diagnosis of hoisting machine vibration signal is a challenging problem and even powerful cyclostationary methods provide ambiguous results. The problem is complex and more efficient methods should be proposed.