Finite-element study of vibration effect to fracture healing of a human tibia

1. Introduction

It is known that living tissues in the process of their growth and development significantly react to the external force field they are functioning in. Mechanical factor takes stimulating and regulating effect to the specific tissue cells, resulting in initiation and development of organ structural transformation processes in the macroscopic aspect [1]. Phenomenon of structural transformation from a soft primitive substance into a solid bone tissue is the result of bone cell differentiation. For example, it takes place during the process of bone continuity regeneration after fracture and skeletal implantation into a bone tissue solid substance that results in initiation of bone remodeling processes in the area of apposition with the surface of the foreign object or between pieces of the broken bone.

Bone has the astonishing capability to repair itself. As a matter of fact, during the bone healing physiological process which initiates immediately after the fracture event, the bone structure will normally get back to its pre-injury state. According to the fracture gap size and the stability of the injured area two main types of bone fracture healing are available: primary and secondary healing. Unlike primary healing with small fracture gap or direct contact between the broken pieces of cortical bone, secondary healing occurs with the presence of some interfragmentary gap, when stabilization is not adequate to allow primary healing. Secondary healing process following a bone fracture, process by which bone fractures heal naturally, is composed by a complex sequence of interlocked events, which can be divided into three overlapping stages – the inflammatory, reparative and remodeling phases [1].

Indeed, starting by the inflammation phase, a hemorrhage, due to the ruptured vessels, firstly fills the fracture interfragmentary gap. Then the reparative phase involves the production of intermediate tissues that stabilize the mechanical environment thanks to two kind of callus, which will successively grow: the soft callus by endochondral ossification (bone formation by a cartilage phase) and the hard callus by intramembranous ossification (direct bone formation), and offer a scaffold for development of new bone tissues. Finally, during the remodeling phase, bone is remodeled and the callus is resorbed [2].

Involving a well-programmed stream of cellular events, bone fracture repair is therefore a complex process of cell differentiation regulated by mechanobiological stimuli, a process which can be studied using computational models [1]. As a matter of fact, mathematical models which relate bone density distribution to the internal loads, like the earliest bone remodeling law presented by Wolff in 1892 [3], are now well accepted by contemporary researchers who agree that bone tissues have mechanoreceptors and that bone trabecular architecture adapts itself to mechanical loads [4, 5].

The mathematical approach conceptually describing the bone tissue regeneration process under impact of the external mechanical stimulus of periodic behavior is considered in the paper. The mathematical model implies that forced interstitial fluid flows induced in the bone pore system due to osseous matrix deformation along with inherent elastic matrix strains are the key mechanical factors regulating bone tissue reparative regeneration. The code for computer simulation of bone regeneration is developed and implemented for numerical analysis of the finite-element model of a human tibia with callus.

2. Mathematical approach for bone reparative regeneration modeling

Based on the research idea firstly proposed by Prendergast et al. [6], and recently used in Lacroix [7] and Isaksson [2] studies, an algorithm describing the bone tissue structural transformation under impact of external mechanical stimuli and where bone tissues are modeled by biphasic materials thanks to the poroelastic medium formulation was created [8].

According to this Prendergast’s theory, as shown in Fig. 1, mesenchymal stem cells are therefore able to differentiate depending on two biophysical stimuli, the fluid velocity in the interstitial fluid phase and the tissue shear strain in the solid phase. As a consequence, high shear strain and fluid flows induce the specialization of the precursor cells into fibroblast with a production of fibrous connective tissue, intermediate stimuli induce the specialization of the precursor cells into chondrocyte with a production of cartilage, and lower stimuli favors osteoblast differentiation and bone remodeling. As a matter of fact, interstitial fluid flows induced in the bone pore system due to osseous matrix deformation along with elastic matrix strains are the key factor regulating bone tissue reparative regeneration.

Fig. 1Tissue differentiation scheme proposed by Prendergast et al. [6, 7]

Using this Prendergast’s approach, a computational code MechanicsFE [5] was designed to investigate the global regeneration process of injured bone elements, as shown below in Fig. 2. This mathematical model provides therefore the possibility to mainly study the impact of the frequency and amplitude of dynamic loads on the bone tissue transformation process during fracture healing.

The calculation model consists of two parallel algorithms based on the single finite element model of the investigated biomechanical object. The first algorithm represents a computational scheme on the base of the diffusion equation and allows to calculate the active precursor cell concentration capable of differentiation and production of other cell types. As the result at each step the three-dimensional concentration distribution of the active cells migrating from the tissues surrounding the bone reparation area is defined by the time.

Fig. 2Block-scheme of algorithm describing the biological tissue transformation

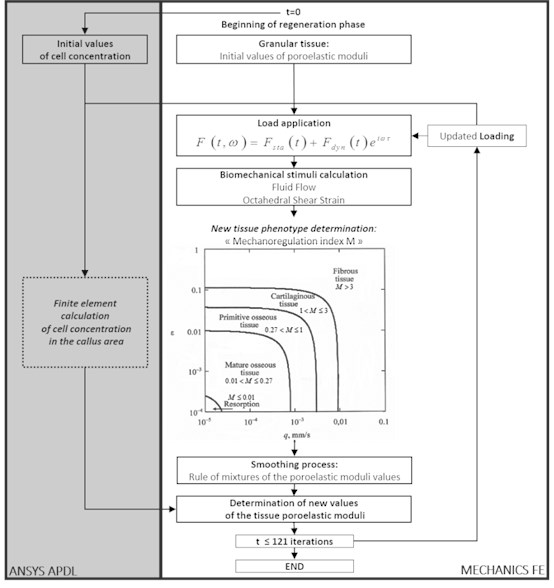
The second part of the structural transformation scheme is dedicated for the calculation of the problem main variables – displacements and deformations of the elastic tissue matrix (the poroelastic medium solid phase), pressure and the interstitial fluid flows. The forces with the certain frequency are applied stepwise according to the specified time rule that allows investigating different load scheme impact to the bone structural transformation mechanism.

After evaluation of the main variables at each point of the poroelastic medium the mechanobiological index $M$ [6, 7] defining, which tissue phenotype is formed under this load stimulation, is calculated using the criterion:

where $\epsilon$ – the maximal value of the octahedral shear strain of the biphasic medium elastic frame, $q$ – the maximal flow rate of the interstitial fluid in the pores, $a=$ 0.0375 and $b=$ 3 μm/s – the empirical constants.

The regeneration model includes, besides the initial granular tissue, four types of the differentiated tissue – the fibrous, cartilaginous, primitive and mature bone tissue. Each of these types is characterized by its own material constant values (density, elastic moduli, penetrability coefficients and etc.). Depending on the index value $M$ Eq. (1) in each node of the finite element model or in the whole finite element the continuous medium poroelastic moduli change.

The mechano-regulation index threshold values are as follows [7]: 1) $M>$3 – the fibrous tissue formation; 2) 1 $<M<$3 – the cartilaginous tissue formation; 3) 0.27$\mathrm{}<M<$ 1 – the formation of the primitive bone tissue with rather high porosity, which is close to the cancellous bone substance; 4) 0.01 $<M<$0.27 – the formation of the mature bone tissue, which is close by its mechanical characteristics to the bone compact substance; 5) $M<$ 0.01 – the bone tissue resorption appearing due to insufficient mechanical stimulation.

The cell concentration in the investigated bone area changes at each step, but the physical and mechanical properties of the material change not at once, because the area occupied by the finite element may partially consist of the differentiated and granular tissue. Therefore, for the evening of the ambiguous material nature and averaging of the element properties a “mixture rule” is applied. New values of the material constants of each finite element describing the bone reparation area are calculated on the base of the obtained averaged values and the concentration values of the active cells at any point of the medium according to the mixture law.

Therefore, at the last phase of the algorithm at each time step the final calculation of the regenerating tissue material constants takes place on account of the active cell concentration values and the values of the corresponding material constants obtained from the finite element analysis of the stress-strain state of the investigated tissue area. Then the physical and mechanical properties of the computational model are refreshed and the numerical scheme is repeated for the following time step. According to the calculation data at each time step one may observe convergence of the process and tendency of the initially undifferentiated homogeneous tissue to transformation into one or another phenotype.

3. Numerical results and discussion

A simplified three-dimensional finite element model of bone together with callus was constructed that takes account of the symmetric formulation of the problem with respect to the three coordinate planes (Fig. 3).

Fig. 3Finite element model of bone together with callus

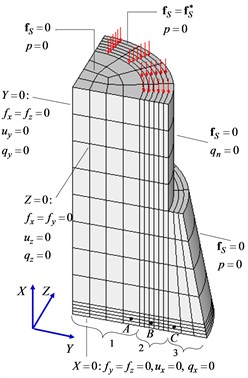
An idealized model of a part of a compact bone is a hollow cylinder of height 28 mm with an outer diameter 20 mm and an inner diameter 14 mm. Callus fills the gap of length 3 mm between the two bone fragments and a region around the bone of length 53 mm and maximum diameter 28 mm. To compare the results with known data and a better understanding of the distinctive features of the mechanism of the regenerative repair of bone tissue, dimensions were chosen corresponding to an axisymmetric model used earlier [7]. The number of finite elements is 528, and the number of degrees of freedom is 11260.

As the distributed load acting on the bone along its longitudinal axis, we consider the sum of a slowly varying compressive force that is constant in each time step and a fast component that varies harmonically with a relatively high frequency.

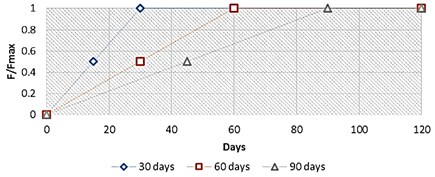
Besides, it is known that a high force on the injured broken bone area is a cause of instability, with a formation of an unstable callus made up only of granular tissues. In fact, in addition of this applied harmonic load, the computational mathematical algorithm included a gradually increasing static force amplitude, starting from a low load value to its maximal value 500 N, reached for a specific limit day (30th, 60th and 90th day), as shown below, and keeping at this level until the end of the bone regeneration process (Fig. 4).

Fig. 4Applied normalized force diagram

The further following results depict the spatial-temporal sequence and evolution of the mechanical properties, and more precisely of the Young’s moduli parameter, of the several bone tissue phenotypes in the specific callus area whereas the bone marrow and the cortical bone are kept their initial Young’s moduli values during all the bone fracture healing process, as shown below in Fig. 5.

Fig. 5Young’s module evolution characterization (harmonic load frequency – 100 Hz, time of reaching static load maximum – 60 days)

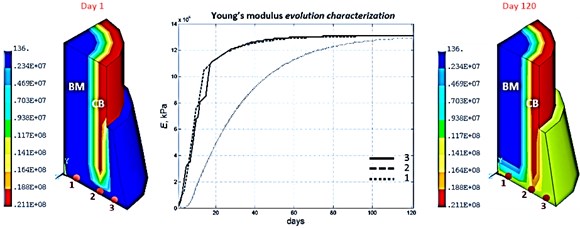
According to the bone regeneration study references [1, 2] bone fracture healing would occur through formation of both an external callus and an internal callus, and with different ossification fronts which stabilize the injured broken bone area. Considering the typical bone reparative regeneration results shown above in Fig. 5 and as expected regarding the clinical results, it’s confirmed that different front of ossification evolving at different rate enable the stabilization of this injured broken bone area.

Indeed, focusing on the numerical results of the Young’s module distribution, it is pointed out that at the beginning of the process at day 5, an ossification starts in the external callus with presence of primitive bone tissues. This ossification front continues its advancement principally toward the bottom of the external callus, concretely fills this specific area and at this same period, day 15, another front of ossification with primitive bone tissues starts in the internal callus, from the cortical bone area to the bone marrow area. Thereafter, these two front of ossification gain ground and at day 30, these internal and external callus connect themselves and start a stabilization of the entire callus by forming a mature bone tissues grid. And finally, from day 30 to the end of the bone reparative regeneration process, these mature bone tissues reinforce themselves by finishing the entire homogenization of these internal and external callus into one global stable callus.

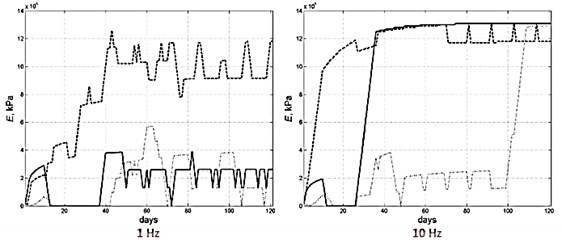
According to numerical studies, there is a complex dependence between the bone transformation mechanism and the applied frequency values. Indeed, applying harmonic load frequency has a significant impact on the different evolutions of the several Young’s moduli values and therefore on the bone tissue phenotype formation (Fig. 6).

According to a qualitative comparison with the earlier bone tissues evolution models [2, 7] the mathematical model developed here provides with credibility the possibility to investigate the bone reparative regeneration process.

Fig. 6Young’s module evolution characterization (harmonic load frequency – 1 and 10 Hz, time of reaching static load maximum – 60 days)

4. Conclusions

The proposed finite-element model of a human tibia with callus provides possibility of the investigation of the regeneration processes of the damaged bone upon the availability of a dynamic load and the theoretical argumentation of the choice of the optimal periodic impact to the damaged tissues for the fastest and stable healing. In particular, the created model allows studying the stimulating harmonic load frequency and amplitude impact to the tissue transformation process, which is completely missing in the well-known references, and the early loading influence to the callus elastic properties restoration as well.

The obtained numerical results are thought to be realistic and corresponding to the well-known medical investigations of the bone tissue regeneration processes in the fracture area.