Dynamics of osteoblasts during bone remodeling cycle

1. Introduction

Bone is a dynamic connective tissue which adjusts to load variations. This adaptation occurs through continuous bone remodeling, which is a result of the dynamic behavior of bone cells. Bone remodeling is a tightly directed procedure assuring the repair of micro damage (targeted rebuilding) and replacing of old bone with new bone tissues. This process occurs through successive osteoclastic resorption and osteoblastic bone formation. Osteoblasts are mesenchymal bone forming cells that are responsible for the synthesis of bone forming matrix called osteoid. Many medical researchers, over the past five to six decades, are studying the dynamic responses of osteoblasts with the help of experimentation. Certain ethical regulations limit the researchers to conduct experiments on living beings. Experimental analysis in vivo is extremely expensive, requires a lot of time and skill which poses as a great challenge to many researchers. This experimental constraint leads to recent studies of the osteoblast cell being carried out numerically and analytically. Finite element analysis enables effective and easier determination of the biomechanical behavior of human subsystems. Simulation techniques potentially reduce the cost and time in the development and analysis of bone cells.

Many researchers have made an attempt to report the responses of osteoblast cultured cells to mechanical stimuli via experimentation. Chow et al. [1] demonstrated the increase of bone formation by 25-30 % for an animal study, at a vertical vibration of 35 Hz with a peak acceleration of 0.3 g. Wang et al. [2] demonstrated the effect of frequency and acceleration amplitude on osteoblast responses. A finite element approach is used to model the osteoblast. The base-excitation responses and resonance frequencies of six different models are reported. While appreciating and respecting the work of the author, it is necessary to point out that the natural frequency reported by the author is referred to previous studies [3, 4] which have compared their natural frequency results with the excitation frequency [5], which is inappropriate. Any system subjected to an excitation frequency is compelled to vibrate at the excitation frequency only, but not at the natural frequency of the system.

The present work is to demonstrate the dynamics of osteoblast cell and exhibition of different natural frequencies during its life cycle. A simple curve fit is carried out to establish a relation between the fundamental natural frequency and the days elapsed for an active osteoblast in bone remodeling cycle. Authentic natural frequencies and the parameters involved for dynamic analysis of micron sized bone cells are highlighted using certain standard approaches.

2. Modeling and simulation

A solid model of an osteoblast cell is developed, considering the three major parts viz., the membrane, cytoplasm and nucleus, using Solid Works. The membrane is a protective layer for the cell, made up of a phospholipid bilayer implanted with proteins. The cytoplasm is a viscous material that is present between the membrane and nucleus. It holds the nucleus in place apart from other organelles in the cell. The nucleus is the most vital part of the cell as it controls the growth, metabolism, synthesis of proteins and stores hereditary information of the cell.

All the three parts are assumed to be isotropic, linear and elastic for the present work. The properties selected are listed in Table 1.

A continuum model approach is used for the investigation. Progressive stages of spreading of an active osteoblast cell over its lifespan of 90 days [6, 7] are modeled in 10 stages. The cytoplasm is modeled as an elastic body with a cavity at its center to accommodate the nucleus. The membrane and the cytoplasm are modeled as a spherical frustum. The membrane thickness is considered as 6 nm [8]. The volume of the cell is kept constant as 3, 000 µm³ [2]. A linear reduction in height ranging from 15.45 µm to 1 µm and corresponding increase in base surface radius from 6.64 µm to 44.60 µm for every 10 days is calculated using the relation:

where $h$ is the instantaneous height, $v$ is the volume and $b$ is the base surface radius of the osteoblast.

The nucleus is modeled with a constant volume (≈105 µm³) [3], as a sphere for models I-VI and as an ellipsoid for models VII-X. Eq. (1) is used to obtain the progressive cell height and base surface radius which are tabulated in Table 2.

During the assembly of the osteoblast model for each stage, the integrity of the three parts is preserved. Models are exported to Ansys (Workbench 18.2). The material properties are assigned as indicated in Table 1. A tetrahedral mesh element with fine mesh size, along with patch confirming method is used to derive a suitable meshing for the entire model. A fixed boundary condition for the base surface is considered. The natural frequencies up to 10 modes are extracted for model I to IX and tabulated in Table 3.

With data obtained from Table 3, a plot is generated between the mode number and the natural frequencies for models I to IX and shown in Fig. 1.

Fig. 1Mode number v/s natural frequencies

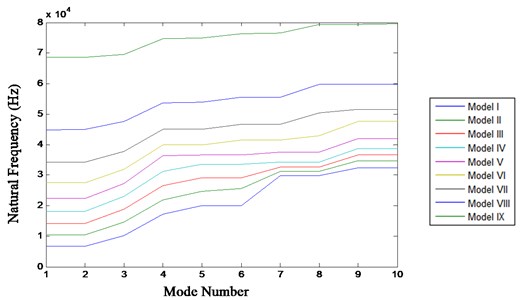
Fig. 1 demonstrates the increase in natural frequencies with every model. It is observed that the stiffness increases as the height of the model decreases, resulting in a simultaneous increase in natural frequency.

A plot is obtained between the fundamental natural frequency and the lifespan of an active osteoblast for the models tabulated in Table 3 which are shown in Fig. 2.

Curve fitting is carried out for the fundamental natural frequencies versus the lifespan for the models I-IX using a cubic function and can be expressed as follows:

This expression can be used to estimate the fundamental natural frequency of an active osteoblast for a given day ($x$). This relation holds good for the initial dimensions and material properties considered for all the parts of the osteoblast. A similar relation can be obtained by using different dimensions and material properties. This serves as a guiding tool to determine the natural frequency an active osteoblast possesses during the bone remodeling cycle and accordingly, the excitation can be initiated. However, depending upon the ratio between the excitation and natural frequency one can estimate the response of the cell.

The corresponding mode shapes for models I to IX are obtained and shown in Figs. 3-5. The dynamic analysis of model X is excluded as osteoblast reaches its final stage and becomes a bone-lining cell.

Fig. 2Number of days v/s natural frequency of an active osteoblast

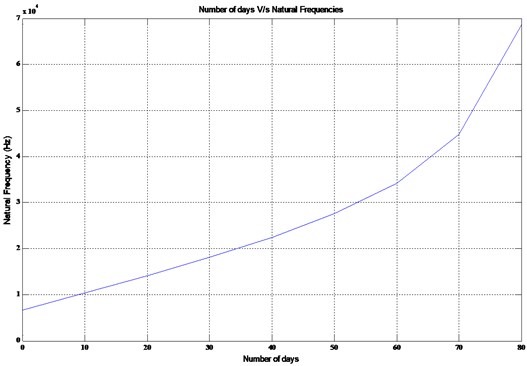
Fig. 3First 4 mode shapes for model I

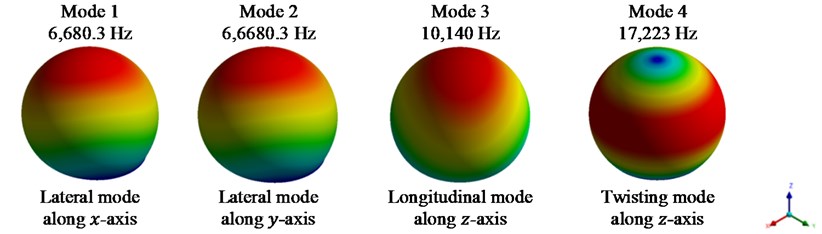
Fig. 4Fundamental mode shape for models II-VIII

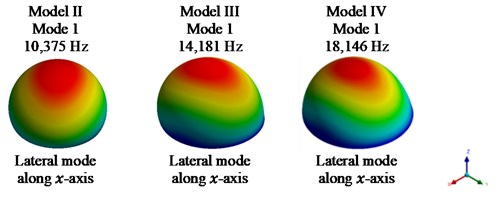
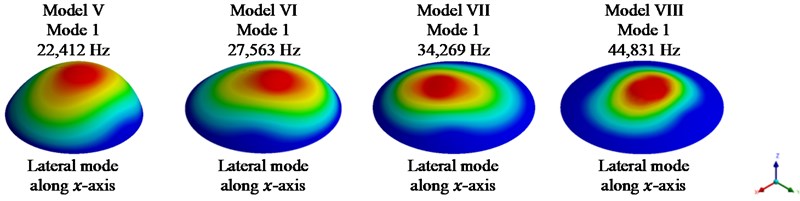
Fig. 3 shows the first four mode shapes for model I. It is observed that the first two natural frequencies are in $x$ and $y$ direction of the system, i.e., lateral mode of vibration. The 3rd mode shape shows a longitudinal vibration in the $z$-direction. A twisting mode shape along the vertical axis, viz., $z$-axis is observed for the fourth natural frequency of the system.

Fig. 4 shows the fundamental mode shapes for models II-VIII in $x$ direction of the system, i.e., lateral mode of vibration.

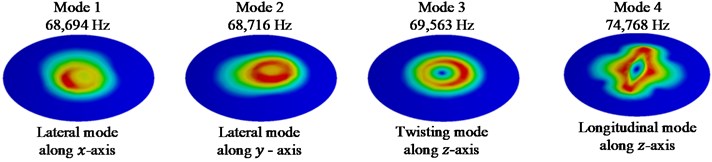
The first four mode shapes for model IX are shown in Fig. 5. Lateral mode of vibration in $x$ and $y$ directions are observed for the first two mode shapes respectively. A twisting mode shape along the $z$- axis is observed for the 3rd natural frequency of the system. The 4th mode is observed to be a longitudinal vibration in $z$-direction.

Fig. 5First 4 mode shapes for model IX

3. Conclusions

The present investigation demonstrates a continuum model approach to analyse the dynamic characteristics of an active osteoblast cell during the bone remodeling cycle. Progressive stages of spreading of an active osteoblast are modeled. An increase in natural frequencies in the range of 6,680-68,694 Hz with reduction in size of every model is reported. Curve fitting is carried out for the fundamental natural frequencies of all 9 models using a cubic function and a mathematical relation is obtained. This mathematical equation holds good for the material and geometrical properties considered in this work. The natural frequency at which an active osteoblast needs to excite for increasing the bone formation rate can be determined with respect to time using this mathematical relation. The response of the osteoblast can be determined depending upon the ratio of excitation frequency to natural frequency of the system.