The study of oscillations of a rotor at the collision with a stator based on the quasidiagonalistic method

1. Introduction

The increase of power and the complication of turbomachineries’ constructions are accompanied by the increase of demands for a vibration. All of it leads to bringing into calculating schemes of rotor machines a number factors, which have been used in calculations of mechanical engineering constructions quite rarely so far, for instance, the real laws of changes of coefficients of dissipation and quasielastic forces in bearings from the angular velocity of a rotating roller. In the regime of picking up speed of rotation from zero to the working frequency a rotor passes through the resonance, and the maximum dimension of removals, depending on the angular velocity of a rotor, may exceed the size of the gap between a sator and a rotor. In this case, as a result, a collision and expensive repairs occur. An approach which is used in this article allows to analyze oscillations of turbomachineries and their separate elements in a relatively simple way without using expensive software products.

2. Description of the quasidiagonalistic method

Lower forms of oscillations mainly contribute to the dynamic reaction of a system of different mechanical engineering processes, and the reactions, which are in congruence with the highest forms of a system, are relatively small. In some cases, it is related to the fact that an external impact’s frequency range is limited, in the other cases decrement is a decisive factor. The method of calculation, based on a special combination of decomposition with condensation of dynamic equations of a mechanical system in accordance with an external impact’s frequency range, is proposed in this article so as to reduce dimension of a problem and make the calculations more stable. Thus, a quasistatic solution is not determined from the original equations of motion. Some simplified equations are used instead of them. Dimension of a simplified system equals the original problem’s dimension. A dissipative or non-dissipative system with no inertness can be taken as an example of a simplified system of equations for calculating a quasistatic constituent. A quasistatic solution will be approximate. It is specified by the second addendum – a dynamic solution. But this specification is carried out only for the forms of oscillations with their natural frequencies belonging to a predetermined private specter of an external impact. It helps to find a dynamic constituent with using a system of equations with significantly lower dimension. This approach has two significant advantages. Firstly, matrixes of inertness and stiffness can be diagonal or block-diagonal. Secondly, the order of a system of dynamic equations is significantly reduced. Moreover, condensation upon a frequency feature leads to the account’s improved stability, as the condition of a matrix that determines stability depends on the highest natural frequency of a system to the lowest one. Let equations of motion of a dissipative system with a finite number of grades of freedom under the influence of an external load in the form of a matrix take the form of Eq. (1):

with initial conditions: $\mathbf{f}\left(0\right)={\mathbf{f}}_{\mathrm{*}}$, $\dot{\mathbf{f}}\left(0\right)={\dot{\mathbf{f}}}_{\mathrm{*}}$. Here $\mathbf{f}\left(t\right)$ is a vector of generalized coordinates, and $\mathbf{M}$, $\mathbf{K}$, $\mathbf{D}$ are matrixes of inertness, stiffness and decrement with dimension ($N\times N$), $\mathbf{R}\left(t\right)$ is a matrix-column of external forces with frequency range [$0,{\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}$]. Let the solution of the original problem Eq. (1) take the form of a sum of two solutions: $\mathbf{f}\left(t\right)={\mathbf{f}}_s\left(t\right)+{\mathbf{f}}_d\left(t\right)$, where ${\mathbf{f}}_s\left(t\right)$ is a quasistatic constituent and ${\mathbf{f}}_d\left(t\right)$ is a dynamic one [1]. Let’s examine two variants of segregation a quasistatic constituent: without taking dissipation Eq. (2) into account:

and with taking dissipation Eq. (3) into account:

Let us note that the solutions to the problems Eq. (2) and Eq. (3) match with the general solution to the problem Eq. (1). Therefore, the solution to the problem Eq. (1) can be replaced by finding the solutions to the subsidiary problems Eq. (2) and Eq. (3), including unknown functions ${\mathbf{f}}_s\left(t\right)$ and ${\mathbf{f}}_d\left(t\right)$. Finding the quasistatic constituent can be done in different ways. Practicularly, straight and interrational ways can be used in findning a solution to this problem. A special combination of decompostion and condensation, which is called the method of quasidiagonalization [1], is used for constructing the dynamic constituent.

Let’s pretend that we are interested in frequency range [$0,{\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}$]. For different variants of identificating the quasistatic constituent of the equation, the reactions which are describing the dynamic constituent of the system result in Eq. (4):

Here index $d$ is omitted. For instance, for the variant of identifing the quasistatic constituent without taking dissipation into account we can write:

Let’s divide the system of equations Eq. (1) in $m$ subsystems (submatrixes) with dimension $N_1$, $N_2$,..., $N_m$. Thus, $N_1+N_2+\dots +N_m=N$. For each $j$-subsystem ${\mathbf{M}}_{jj}{\ddot{\mathbf{f}}}_j\left(t\right)+{\mathbf{K}}_{jj}{\mathbf{f}}_j\left(t\right)=0$ we solve the problem, get peculiar meanings ${\mathbf{V}}_j^T{\mathbf{M}}_{jj}{\mathbf{V}}_j={\mathbf{E}}_{N_j}\text{,}$${\mathbf{V}}_j^T{\mathbf{K}}_{jj}{\mathbf{V}}_j={\mathrm{\Omega }}_{N_j}^2$ and enter the transformation:

where $\mathbf{w}\left(t\right)$ is a vector of new variables, ${\mathbf{V}}_{n_j}$ are the forms, that are describing the oscillations with natural frequencies belonging to the range of [$0,{\theta }_j$], ${\mathbf{V}}_{N_j-n_j}$ are the forms beyond this range, $n_j$ is a number of grades of freedom of the$j$-subsystem, their natural frequencies ${\omega }_{jk}$ satisfy the following conditions :${\omega }_{j1}\le {\omega }_{j2}\le ...\le {\omega }_{j{n}_j}\le {\theta }_j$, ${\omega }_{j{n}_j+1}>{\theta }_j$, and besides ${\theta }_j$ is the upper linit of the $j$-subsystem‘s frequency range, which is chosen from the condition ${\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}^2/{\omega }_{j{n}_j+1}^2\ll 1$, ${\mathbf{E}}_n$ is a single matrix with dimension ($n\times n$),$n=n_1+n_2+...+n_m$, ${\stackrel{-}{\mathbf{K}}}_{N-n,N-n}^{}={\mathbf{V}}_{N-n}^T\mathbf{K}{\mathbf{V}}_{N-n}^{}$, ${\stackrel{-}{\mathbf{K}}}_{N-n,n}={\mathbf{V}}_{N-n}^T\mathbf{K}{\mathbf{V}}_n^{}.$

If we substitute Eq. (5) into Eq. (4), we get a reduced system of equations with the following order $n=n_1+n_2+\dots +n_m$:

where:

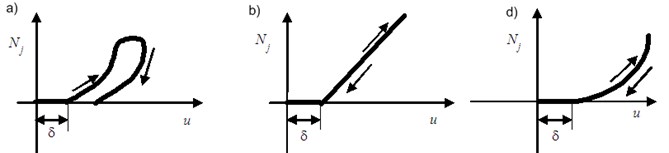
The Eq. (6) has two significant advantages. Firstly, the matrixes can be diagonal or block-diagonal. Secondly, the order of the system of linear equations is reduced from $N$ to $n.$ Moreover, condensation upon a frequency feature leads to the account’s improved stability, as the condition of the matrix ${{\stackrel{-}{\mathbf{M}}}_n^{\mathrm{*}}}^{-1}{\stackrel{-}{\mathbf{K}}}_n^{\mathrm{*}}$ that determines the stability depends on the ratio of the highest natural frequency of the system to the lowest. When the rotor has a contact with the stator in the $j$-cross section, normal force of reaction $N_j\left(t\right)$ from the side of the stator and force of friction $T_j\left(t\right)$, which is applied to the rotor on a tangent at the contact point appear. Normal force at the contact spot is a significantly nonlinear function. It takes the form of a hysteresis loop “force-deformation” $N_j=f(u,\dot{u})$ (Fig. 1(a)), which takes into account not only deformation of the stator (Fig. 1(b), (d)), but the direction of deformation velocity. Thus, forces of interaction between the rotor and the stator in the$j$-cross section are nonlinear and can be written in the form of:

Here $u_j\left(t\right)=\sqrt{u_{xj}^2\left(t\right)+u_{yj}^2\left(t\right)}$ is a radial removal of the rotor at the contact spot; $f_j$ is a coefficient of sliding friction; $\delta$ is the gap between the rotor and the stator; $K_{stj}$ is the stator’s stiffness, which is determined at each step of the solution as the ratio of the normal force to the dimension $(u_j-\delta )$.

In case of the rotor hurting the stator in the equations Eq. (2) or Eq. (3) there will appear nonlinear members, which take into account the stator’s stiffness at the contact spot with the rotor:

Therefore, during the process of the contact “rotor-stator” a nonlinear matrix of the stator’s stiffness has to be added at the contact spot Eq. (7) to the global matrix of stiffness in the equations of motion Eq. (2) or Eq. (3).

Fig. 1Normal force at the contact spot “rotor-stator”

3. Some numerical results

Let’s examine unsettled oscillations of a symmetrical single-disk rotor (Fig. 2), that hangs on two identical bearings with taking into account the contact between the rotor and the stator. We take as initial data: the disk’s weight $m=$5000 kg; axial moment of the disk‘s inertness $J_m=\mathrm{}$165$\mathrm{}$kg m${\mathrm{}}^2$; length $a=\mathrm{}$2,0 m; unsettled $\epsilon$ is centered in the average cross section and equals 10; bending stiffnesses of the cross section $E{J}_x=E{J}_y$$=\mathrm{}$0,3∙10⁹ Nm², the stator’s stiffness $K_{st}=$ 10⁸ N/m (Fig. 1(b)), the gap between the rotor and the stator $\delta =\mathrm{}$0,0018 m, the coefficient of sliding friction between the stator and the rotor $f=\mathrm{}$0,15.

Fig. 2The finite element model of the rotor

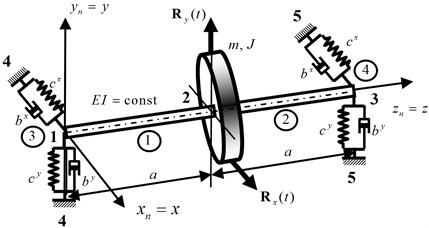
Let’s pretend that the rotor is a summation of finite elements with five junctions (Fig. 2). The formation of global matrixes of inertness, stiffness, decrement and the vector of junctive loads is written up in [2-4]. The processes of unsettled oscillations in the launching regime and no-load idle at the angular acceleration $\beta =$ 50 s^-2 are shown in Fig. 3, where dynamic removals of the rotor’s disk in two orthogonal planes $Xoz$, $Yoz$ (the solid line and the dashed one accordingly).

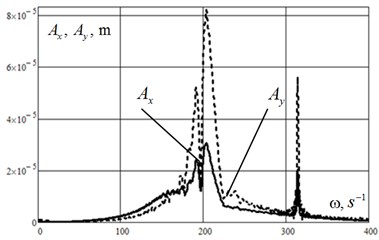
The graphics on Fig. 3 show the rotor passing the first resonance and the second one, when instantaneous frequency of stimulative force $\theta =\beta t$ at given time $t_{\mathrm{*}x}=p_{1x}/\beta$, $t_{\mathrm{*}y}=p_{1y}/\beta$ equals the first natural frequency of the rotor and the second one $p_{1x}=\text{149,164}$ s^-1, $p_{1y}=\text{202,534}$ s^-1. During the process of the rotor passing the second resonance its collision with the stator happens. Normal force of reaction $N\left(t\right)$ from the rotor to the stator is shown on Fig. 4. After the rotor passing the second resonance the oscillations reach the established regime. Fig. 5 shows the amplitude specter of the oscillatory process in a horizontal plane and in a vertical one. Fig. 6 shows that the oscillatory process includes three main components: $p_{1x}=\text{160}$ s^-1, $p_{1y}=\mathrm{}$202 s^-1 and ${\theta }_p=\mathrm{}$314 s^-1. Thus, the last one corresponds to the established oscillations with circular rotation speed ${\theta }_p$.

Fig. 3Unsettled forced oscillations of the rotor’s disk (junction 2, Fig. 2)

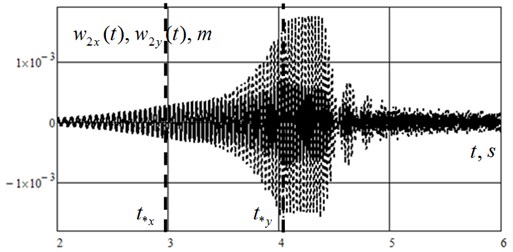
Fig. 4Normal force of collision of a rotor with a stator

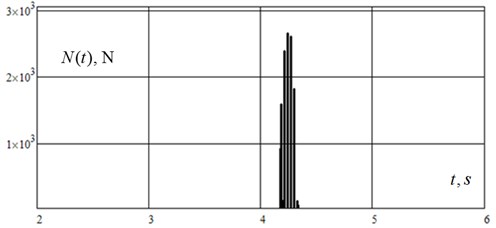
Fig. 5The amplitude specter of the rotor’s disk

4. Conclusions

Thus, the analysis of the results shows that the quasidiagonalistic method gives a complacent estimate of the results’ accuracy [1, 3]. Moreover, it allows to significantly reduce the problem’s dimension (in the considered example – on 30 %) and improve the account’s stability.