Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine

Zhu, Rui; Zhang, Yanru; Ren, Jianxing; Li, Hongguang; Han, Qingkai

doi:10.21595/jve.2016.17491

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2017

Check for updates

Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine

Rui Zhu¹

Yanru Zhang²

Jianxing Ren³

Hongguang Li⁴

Qingkai Han⁵

^{1, 2, 3}College of Energy and Mechanical Engineering, Shanghai University of Electric Power, Shanghai, China

^{4, 1}State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai, China

⁵School of Mechanical Engineering, Dalian University of Technology, Dalian, China

Corresponding Author:

Rui Zhu

Cite the article Download PDF

Downloads 1621

WoS Core Citations 5

CrossRef Citations 4

Abstract

Most of the major faults in gas turbines often originate from the rotor shaft. Some of these faults could result to misalignment, imbalance, crack, rub-impact and eccentricity. This study analyzes nonlinear factors such as lube-film surge and thermal-stress. Seal and bearing quality significantly affect the performance of a rotor system. The nonlinear dynamic characteristics of a high-temperature rotor–bearing–seal coupled system are investigated. Dynamic trajectories, Poincaré maps, frequency spectra diagrams are used to analyze the features of the rotor-bearing-seal coupled system in terms of various parameters. Several nonlinear phenomena in the high-temperature rotor–bearing–seal coupled system, such as periodic, double-periodic, multi-periodic, and quasi-periodic motion are investigated. Through these curves and the program, the dynamic characteristics of gas turbine rotors could be easily and accurately calculated. To validate this method, the critical speed of a real rotor of an actual gas turbine was calculated by means of the program and curves. The results are consistent with the measured data and may contribute to further understanding the nonlinear dynamics of the high-temperature rotor-bearing-seal coupled system.

1. Introduction

Gas turbines efficiently generate clean power and have been extensively applied because of its global market demand. As one of the key components of the gas turbine, the performance of a rotor directly affects the engine efficiency. With the recent technological advancements, rotors are being developed toward having towards large span, possessing more flexibility and carrying heavier load. However, rotors are constantly exposed to high temperature and harsh environment, thereby making them prone to failure. Rotor failure usually results to rubbing, imbalance, crack and other phenomena. Therefore, research on the mechanism of fluid-solid interaction in the rotor-bearing-seal system is crucial for improving modern rotating machines.

In the early stage of rotor dynamics, study on the rotor-bearing sealing system used linear models. However, linear theory failed to explain a number of phenomena; thus, nonlinear theory gradually developed. For a better simulation of bearing nonlinearity, some nonlinear seal force models have been proposed. The present study adopts the Muszynska [1, 2] model to describe the sealing force considering that such model can describe the nonlinear characteristics of the sealing force and has a clear physical meaning.

Based on Muszynska nonlinear seal force model, Ding et al. [3, 4] investigated an unstable mechanism with the single-disc rotor seal system and then analyzed the direction of Hopf bifurcation and the influence of instability on the unbalance mass. In another paper, Ding et al. [5] analyzed the Hopf bifurcation behavior of a symmetric rotor-seal system by using Muszynska nonlinear seal fluid dynamic force model. Moreover, Li et al. [6-8] studied both the dynamic stability and imbalance in the rotor system by adopting the aerodynamic force of the labyrinth seal in the Muszynska mode. Wang [9, 10] proposed and validate a hybrid numerical method to calculate pressure distribution of ultra-short gas bearing system and rotor orbits. In his another papers, Wang utilize this method to confirm the changes of rotor nonlinear dynamic behavior and bearing systems characterized as the rotor mass is increased, the results indicated that the method is useful for gas bearing systems. In addition, the rotor becomes unstable when a certain rotational speed is reached and when the whirl amplitude increases along with the increasing speed. At very high speeds, the seal and the rotor would rub. What is more, the seal force models have also been developed by many other researchers. In order to study the characteristics of the rotor motion, He et al. [11] presented a new nonlinear sealing force model based on the double control body model and rotor motion equation with drawing the trajectory of the rotor, Poincare and bifurcation diagram. Moreover, Yan et al. [12] proposed a transient CFD method for analyzing the complex annular seals of the rotor-seal coupled system. Their findings show that the system exhibits complex dynamic behavior and possible chaotic motion as the rotor speed increases. The pressure ratio has a significant effect on the frequency response of the first-order critical speed; however, it does not significantly affect the motion state and the frequency response of the rotating speed.

Some nonlinear oil-film force models have been proposed to better simulate the nonlinearity of the sliding bearing. Jing et al. [13] proposed a continuum model that is based on the finite element method to analyze the oil whip phenomenon. For the oil-whirl and oil-whip phenomena, Castro et al. [14] employed a nonlinear force model to perform a detailed analysis to verify the effects of unbalance, journal-bearing parameters and rotor arrangement (vertical or horizontal) on the instability threshold. Leng et al. [15] simulated the rotor movement, the traditional eight stiffness, and the damping coefficient of the linear system response under the oil film force model when the speed increases by comparing the analysis made after considering the nonlinear oil film force characteristics of the rotational speed of the oil film when oscillation occurs in advance. Zhang et al. [16] developed a mathematical model and a computational methodology to simulate the complicated flow behaviors of the journal micro-bearing in the slip regime. Their findings indicated that the rotary motion was stable and exhibited half-frequency whirling when the system located in the lower stability region, whereas the rotary motion displayed high-frequency whirling when the system was located in the upper stability region. Riemann et al. [17] stated the rotor instabilities are related to the operational speed and structural parameters. They used the $μ$ -synthesis control technique to reduce the oil whip instability. Furthermore, Yang et al. [18] proposed a new nonlinear dynamic analysis method mainly to analyze the effects of mass eccentricity on dynamic behaviors of rotor system supported by oil-film journal bearings. Ma et al. [19] investigated the influence of angular acceleration, parallel misalignment, and angular misalignment on the oil-film instability of a flexible rotor-bearing system in the run-up and run-down processes at high speeds. In the run-up process, lower misalignment levels delay the onset of the second vibration mode instability; however, instability may occur in advance under high misalignment levels. Furthermore, the amplitudes of multiple frequency components under parallel misalignment conditions are more evident than amplitudes under the angular misalignment conditions. Sekhar et al. [20] introduced two different approach to identify the unbalanced fault in a rotor system: equivalent loads minimization method and vibration minimization method. The combination of equivalent loads minimization method with the modified theoretical fault model and vibration minimization method is more effective than using the equivalent load minimization method in identifying unbalance fault. Dufour et al. [21] proposed an on-board rotor model to investigate the nonlinear dynamics of a support-excited flexible rotor with hydrodynamic journal bearings. Compared with the rigid bearings, linearized hydrodynamic bearings have greater influence on the size of the instability regions of the rotor.

Many researchers investigated the dynamic behaviors of the rotor-bearing-seal system in relation to the coupling effect of the nonlinear oil film force and seal force. Previous literature [22-27] combined nonlinear oil film force model with Muszynska seal force model to study the nonlinear dynamics behavior and stability of rotor bearing sealing system. By comparing the response of the rotor system with the sealing force, it was found that the nonlinear sealing force can improve the stability region of the rotor system and the complex behavior was suppressed. The effect of changing the rotational speed, eccentricity, or sealing gap parameter on the rotor system was also studied. Shen et al. [28] conducted a theoretical and experimental study to analyze the nonlinear dynamic behavior of the rotor-bearing seal system. Their investigation showed that the seal force would reduce the system threshold of instability and the vibration amplitude of the rotor system. Ma et al. [29] studied the influence of speed and eccentricity of the sealing force on the rotor-bearing seal system under two kinds of load conditions. The nonlinear oil-film force model was based on the assumption that short bearings are used. Research shows that the sealing force can improve the critical speed, whereas second-order speed does not have a significant effect on critical speed. Moreover, Ma et al. [30] adopted a mathematical approach to investigate the influence of rotational speed on the dynamic characteristics of the seal with another circular bearing oil film force model of Capone. The time domain, frequency spectrum, phase and Poincare diagrams under different speeds are calculated. Results reveal the influence of rotational speed on the nonlinear vibration of the rotor.

Thermal stress can also significantly influence on the rotary system. Zhu et al. [31-33] employed the finite element method to study the internal temperature distribution of steam turbine components which results in large thermal deformation and thermal vibration of the rotor. The influence of radial temperature difference, imbalance, heat bending and the combined action on the thermal vibration characteristics of the rotor bearing system is analyzed by using thermal structure dynamics coupling theory. Results showed that thermal bending alters the vibration characteristics of the rotor system. This study focuses on the rotor-bearing-seal system in gas turbines under thermal stress.

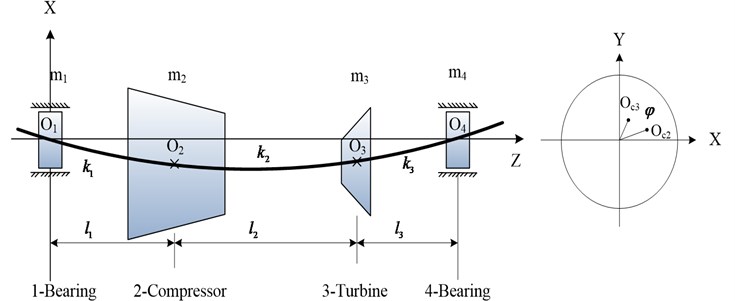
2. Mathematical model of a rotor-bearing-seal system with two discs

In order to study nonlinear dynamic behavior efficiently, a mathematical model of a rotor-bearing seal system, which is depicted in Fig. 1.

Fig. 1Nonlinear rotor-bearing-seal system of the gas turbine

2.1. Equation of motion

1

m_{1} X_{1}^{''} + C X_{1}^{'} + K_{1} (X_{1} - X_{2}) = f_{X} + f_{T},

m_{1} Y_{1}^{''} + C Y_{1}^{'} + K_{1} (Y_{1} - Y_{2}) = f_{Y} - m_{1} g + f_{T},

m_{2} X_{2}^{''} + C X_{2}^{'} + K_{2} (X_{2} - X_{3}) + K_{1} (X_{2} - X_{1}) = F_{X} + m_{2} r ω^{2} c o s ω t + f_{T},

m_{2} Y_{2}^{''} + C Y_{2}^{'} + K_{2} (Y_{2} - Y_{3}) + K_{1} (Y_{2} - Y_{1}) = F_{Y} + m_{2} r ω^{2} s i n ω t - m_{2} g + f_{T},

m_{3} X_{3}^{''} + C X_{3}^{'} + K_{2} (X_{3} - X_{2}) + K_{3} (X_{3} - X_{4}) = F_{X} + m_{3} r ω^{2} c o s ω t + f_{T},

m_{3} Y_{3}^{''} + C Y_{3}^{'} + K_{2} (Y_{3} - Y_{2}) + K_{3} (Y_{3} - Y_{4}) = F_{Y} + m_{3} r ω^{2} s i n ω t - m_{3} g + f_{T},

m_{4} X_{4}^{''} + C X_{4}^{'} + K_{3} (X_{4} - X_{3}) = f_{X} + f_{T},

m_{4} Y_{4}^{''} + C Y_{4}^{'} + + K_{3} (Y_{4} - Y_{3}) = f_{Y} - m_{4} g + f_{T} .

where, $m_{1}$ – the left journal mass; $m_{2}$ – mass of the left disc; $m_{1}$ – mass of the right disc; $m_{4}$ –the right journal mass; $C$ – system damping; $K_{1}$ , $K_{2}$ , $K_{3}$ – stiffness matrix of the system; $X_{1}$ , $Y_{1}$ –the journal displacement; $X_{2}$ , $Y_{2}$ – displacement of the left disc center; $X_{3}$ , $Y_{3}$ – displacement of the right disc center; $X_{4}$ , $Y_{4}$ – the right journal displacement; $r$ – eccentricity of the disc; $f_{X}$ , $f_{Y}$ – the oil-film forces in x and y directions; $F_{X}$ , $F_{Y}$ – the seal forces in x and y directions; $f_{T}$ – thermal stress.

2.2. Nonlinear oil-film force and thermal stress

Nonlinear oil-film force [34] based on the assumption of short bearings can be calculated as:

2

f_{X} = σ \bar{f_{x}}, f_{Y} = σ \bar{f_{y}},

3

σ = μ ω R L {(\frac{R}{C_{b i}})}^{2} {(\frac{L}{2 R})}^{2}, (i = 1,4),

4

[\begin{array}{l} \bar{f_{x}} \\ \bar{f_{y}} \end{array}] = - \frac{{[{(x - 2 y^{'})}^{2} + (y + 2 x')^{2}]}^{\frac{1}{2}}}{1 - x^{2} - y^{2}} \times [\begin{array}{l} 3 x V (x, y, α) - s i n α G (x, y, α) - 2 c o s α S (x, y, α) \\ 3 y V (x, y, α) + c o s α G (x, y, α) - 2 s i n α S (x, y, α) \end{array}],

5

V (x, y, α) = \frac{2 + (y c o s α - x s i n α) G (x, y, α)}{1 - x^{2} - y^{2}},

6

S (x, y, α) = \frac{x c o s α + y s i n α}{1 - (x c o s α + y s i n α)^{2}},

7

G (x, y, α) = \frac{2}{(1 - x^{2} - y^{2})^{\frac{1}{2}}} [\frac{π}{2} + a r c t g \frac{y c o s α - x s i n α}{(1 - x^{2} - y^{2})}],

8

α = a r c t a n \frac{y + 2 x'}{x - 2 y'} - \frac{π}{2} s g n (\frac{y + 2 x^{'}}{x - 2 y^{'}}) - \frac{π}{2} s g n (y + 2 x^{'}),

where, $σ$ – Sommerfeld number; $μ$ – lubricant viscosity; $L$ – the bearing length; $C_{b 1}$ – the left bearing clearance; $C_{b 4}$ – he right bearing clearance; $C_{s}$ – the seal clearance; $R$ – the bearing radius; $\bar{f_{x}}$ , $\bar{f_{y}}$ – the dimensionless nonlinear oil-film forces.

Assume the temperature field is steady, the heat conduction equation for steady temperature field [31]:

9

\frac{d^{2} T}{d x^{2}} + \frac{d^{2} T}{d y^{2}} = 0 .

Introduce the thermal boundary conditions:

10

{T|}_{Γ} = T_{0} .

Thermal stress caused by the steady state temperature:

11

f_{T} = \frac{E α}{1 - υ} (\bar{T} - T_{0}),

where, $α$ – thermal expansion coefficient; $E$ – elastic modulus; $υ$ – Poisson ratio; $T_{0}$ – environment temperature of rotor system; $\bar{T}$ – surface temperature of rotor.

2.3. Nonlinear seal force

Muszynska model is used to describe the nonlinear seal force because it not only reflects the nonlinear characteristics of seal force but also describes a clear physical meaning:

12

[\begin{array}{l} F_{x} \\ F_{y} \end{array}] = - [\begin{matrix} K_{f} - m_{f} τ_{f}^{2} ω^{2} & τ_{f} ω D_{f} \\ - τ_{f} ω D_{f} & K_{f} - m_{f} τ_{f}^{2} ω^{2} \end{matrix}] [\begin{array}{l} X \\ Y \end{array}] - [\begin{matrix} D_{f} & 2 τ_{f} m_{f} ω \\ - 2 τ_{f} m_{f} ω & D_{f} \end{matrix}] [\begin{array}{l} X^{'} \\ Y^{'} \end{array}]

- [\begin{matrix} m f & 0 \\ 0 & m f \end{matrix}] [\begin{array}{l} X^{''} \\ Y^{''} \end{array}] .

In Eq. (12): $K_{f}$ – equivalent stiffness; $m_{f}$ – equivalent mass; $D_{f}$ – equivalent damping; $τ_{f}$ – fluid average circumferential velocity ration; $ω$ – rotational speed:

13

K_{f} = K_{0} (1 - e_{f}^{2})^{- n}, D_{f} = D_{0} (1 - e_{f}^{2})^{- n}, τ_{f} = τ_{0} (1 - e_{f})^{b}, 0 < b < 1,

14

e_{f} = \frac{\sqrt{x^{2} + y^{2}}}{C_{s}} .

Furthermore, $K_{0}$ , $D_{0}$ in Eq. (13) are given by Childs [35]:

15

K_{0} = μ_{3} μ_{0}, D_{0} = μ_{1} μ_{3} T_{f}, T_{f} = \frac{l_{f}}{υ} .

16

μ_{0} = \frac{2 σ^{2}}{1 + ξ + 2 σ} E_{f} (1 - m_{0}), μ_{1} = \frac{2 σ^{2}}{1 + ξ + 2 σ} [\frac{E_{f}}{σ} + \frac{B}{2} (\frac{1}{6} + E_{f})],

μ_{2} = \frac{σ}{1 + ξ + 2 σ} (\frac{1}{6} + E_{f}), μ_{3} = \frac{π R_{f} Δ P}{λ},

In order to facilitate calculation and avoid excessive truncation errors, the dimensionless transformations are given as follows:

18

ω t = τ_{f}, x_{1} = \frac{X_{1}}{C_{b 1}}, y_{1} = \frac{Y_{1}}{C_{b 1}}, x_{2} = \frac{X_{2}}{C_{s}}, y_{2} = \frac{Y_{2}}{C_{s}},

x_{3} = \frac{X_{3}}{C_{s}}, y_{3} = \frac{Y_{3}}{C_{s}}, x_{4} = \frac{X_{4}}{C_{b 4}}, y_{4} = \frac{Y_{4}}{C_{b 4}},

19

ω \frac{d}{d t} = \frac{d}{d τ_{f}}, ω^{2} \frac{d^{2}}{d t^{2}} = \frac{d^{2}}{d τ_{f}^{2}},

20

x^{'} = \frac{d x}{d τ_{f}}, y^{'} = \frac{d y}{d τ_{f}}, x^{''} = \frac{d^{2} x}{d τ_{f}^{2}}, y^{''} = \frac{d^{2} y}{d τ_{f}^{2}} .

Taking the oil-film force, thermal stress and seal force substitute into the Eq. (1), then the dimensionless equations are carried out:

21

x_{1}^{''} + \frac{C}{m_{1} ω} x_{1}^{'} + \frac{K_{1}}{m_{1} ω^{2}} x_{1} - \frac{K_{1} C_{s}}{m_{1} C_{b 1} ω^{2}} x_{2} = \frac{σ}{m_{1} C_{b 1} ω^{2}} \bar{f_{x}} + \frac{f_{T}}{m_{1} C_{b 1} ω^{2}},

y_{1}^{''} + \frac{C}{m_{1} ω} y_{1}^{'} + \frac{K_{1}}{m_{1} ω^{2}} y_{1} - \frac{K_{1} C_{s}}{m_{1} C_{b 1} ω^{2}} y_{2} = \frac{σ}{m_{1} C_{b 1} ω^{2}} \bar{f_{y}} - \frac{g}{C_{b 1} ω^{2}} + \frac{f_{T}}{m_{1} C_{b 1} ω^{2}},

x_{2}^{''} + \frac{C}{(m_{2} + m_{f}) ω} x_{1}^{'} + \frac{K_{1}}{(m_{2} + m_{f}) ω^{2}} (x_{2} - \frac{C_{b 1}}{C_{s}} x_{1}) + \frac{K_{2}}{(m_{2} + m_{f}) ω^{2}} (x_{2} - x_{3})

= \frac{\bar{F_{x}}}{(m_{2} + m_{f}) ω^{2}} + \frac{m_{2} r c o s τ_{f}}{(m_{2} + m_{f}) C_{s}} + \frac{f_{T}}{(m_{2} + m_{f}) C_{s} ω^{2}},

y_{2}^{''} + \frac{C}{(m_{2} + m_{f}) ω} y_{2}^{'} + \frac{K_{1}}{(m_{2} + m_{f}) ω^{2}} (y_{2} - \frac{C_{b 1}}{C_{s}} y_{1}) + \frac{K_{2}}{(m_{2} + m_{f}) ω^{2}} (y_{2} - y_{3})

= \frac{\bar{F_{y}}}{(m_{2} + m_{f}) ω^{2}} + \frac{m_{2} r s i n τ_{f}}{(m_{2} + m_{f}) C_{s}} - \frac{m_{2} g}{(m_{2} + m_{f}) C_{s} ω^{2}} + \frac{f_{T}}{(m_{2} + m_{f}) C_{s} ω^{2}},

x_{3}^{''} + \frac{C}{(m_{3} + m_{f}) ω} x_{3}^{'} + \frac{K_{2}}{(m_{2} + m_{f}) ω^{2}} (x_{3} - x_{2}) + \frac{K_{3}}{(m_{2} + m_{f}) ω^{2}} (x_{3} - \frac{C_{b 4}}{C_{s}} x_{4})

= \frac{\bar{F_{x}}}{(m_{3} + m_{f}) ω^{2}} + \frac{m_{2} r c o s τ_{f}}{(m_{3} + m_{f}) C_{s}} + \frac{f_{T}}{(m_{3} + m_{f}) C_{s} ω^{2}},

y_{3}^{''} + \frac{C}{(m_{3} + m_{f}) ω} y_{3}^{'} + \frac{K_{2}}{(m_{3} + m_{f}) ω^{2}} (y_{3} - y_{2}) + \frac{K_{3}}{(m_{2} + m_{f}) ω^{2}} (y_{3} - \frac{C_{b 4}}{C_{s}} y_{4})

= \frac{\bar{F_{y}}}{(m_{3} + m_{f}) ω^{2}} + \frac{m_{3} r s i n τ_{f}}{(m_{3} + m_{f}) C_{s}} - \frac{m_{3} g}{(m_{3} + m_{f}) C_{s} ω^{2}} + \frac{f_{T}}{(m_{3} + m_{f}) C_{s} ω^{2}},

x_{4}^{''} + \frac{C}{m_{4} ω} x_{4}^{'} + \frac{K_{3}}{m_{4} ω^{2}} (x_{4} - \frac{C_{s}}{C_{b 4}} x_{3}) = \frac{σ}{m_{4} C_{b 4} ω^{2}} \bar{f_{x}} + \frac{f_{T}}{m_{4} C_{b 4} ω^{2}},

y_{4}^{''} + \frac{C}{m_{4} ω} y_{4}^{'} + \frac{K_{3}}{m_{4} ω^{2}} (y_{4} - \frac{C_{s}}{C_{b 4}} y_{3}) = \frac{σ}{m_{4} C_{b 4} ω^{2}} \bar{f_{y}} - \frac{g}{C_{b 4} ω^{2}} + \frac{f_{T}}{m_{4} C_{b 4} ω^{2}} .

$\bar{F_{x}}$ , $\bar{F_{y}}$ are the dimensionless sealing force that written by:

22

[\begin{array}{l} \bar{F_{x}} \\ \bar{F_{y}} \end{array}] = - [\begin{matrix} K_{f} - m_{f} τ_{f}^{2} ω^{2} & τ_{f} ω D_{f} \\ - τ_{f} ω D_{f} & K_{f} - m_{f} τ_{f}^{2} ω^{2} \end{matrix}] [\begin{array}{l} x \\ y \end{array}] - ω [\begin{matrix} D_{f} & 2 τ_{f} m_{f} ω \\ - 2 τ_{f} m_{f} ω & D_{f} \end{matrix}] [\begin{array}{l} x^{'} \\ y^{'} \end{array}] .

3. Analysis of experimental results

In this study, the rotor-bearing seal system of gas turbines is simplified into a double-disc rotor-bearing model, and two different sliding bearings with different diameters provide support at both ends. In a bearing with oil film force, sealing force is applied on the disc, which is a more common model.

Rotational speed has a significant influence on rotary movement. Rotors generally start with slow rotations under low rotational speed. As the speed gradually increases, the rotor will also increase its rotational speed, such as double-periodic motion, quasi-periodic motion and the resonance of first-order critical speed. However, after the first-order critical speed has been achieved and the speed continues to increase, rotary movement will change gradually from the nonstationary stage to the smooth stage. Analytical results presented in Fig. 2 to Fig. 4 are based on different speeds under the same temperature. Axis orbit, time-domain waveform, spectrogram, waterfall and Poincaré maps are showned in the Fig. 2. Poincaré maps can be interpreted as a discrete dynamical system. The stability of a periodic orbit of the original system is closely related to the stability of the fixed point of the corresponding Poincaré map. The multiple frequency components of the spectrum and Poincaré map presented in Fig. 2 indicate that the system is in a quasi-periodic motion. However, with the speed continuing to increase as shown in Fig. 3 and Fig. 4, the movement of the rotor system changes gradually toward the transition to stable region, and harmonic components will continue to reduce. This condition reflects the principle by which the supercritical unit operates: when the speed exceeds the critical speed, the increase in a certain range of speed will stabilize the system further.

Figs. 7 to 9 present the original data and the data after the five-layer and six-layer wavelet transforms, respectively. The waveforms of the original data indicate that the system is in a quasi-periodic motion rather than in a periodic motion and that multiple frequency components are observed in the spectrum. Fig. 6 presents the analytical result after five-layer wavelet processing which shows that only the fundamental frequency components (2X and 3X) were retained. Fig. 7 presents a more detailed analysis of the six-layer wavelet transform where only a fundamental frequency was retained.

Fig. 2Quasi-Periodic motion

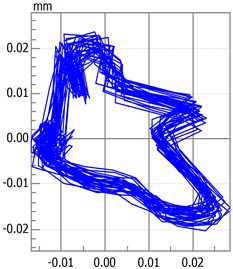
a) Axis orbit

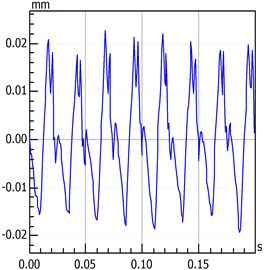
b) Time-domain waveform

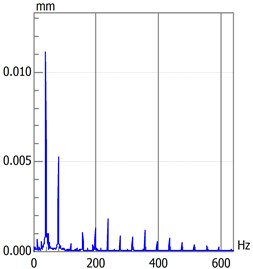
c) Spectrogram

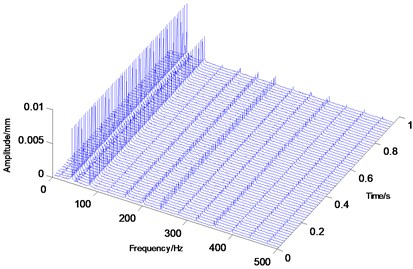
d) Waterfall

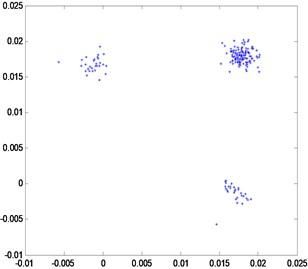
e) Poincaré map

Fig. 3Quasi-Periodic motion

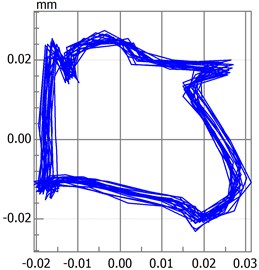
a) Axis orbit

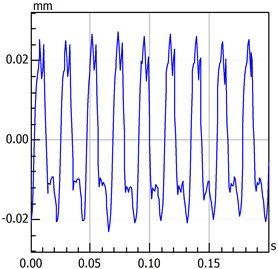
b) Time-domain waveform

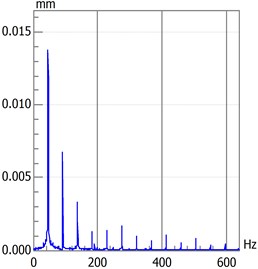
c) Spectrogram

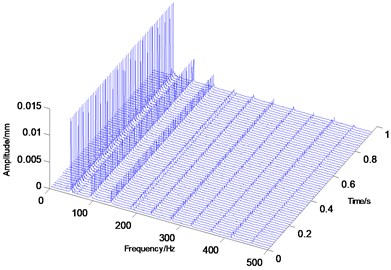
d) Waterfall

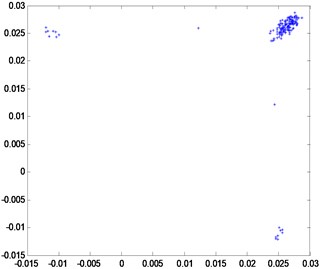
e) Poincaré map

Fig. 4Period doubling motion

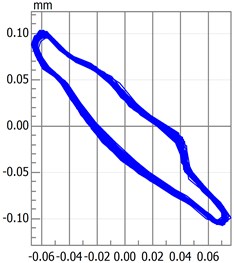
a) Axis orbit

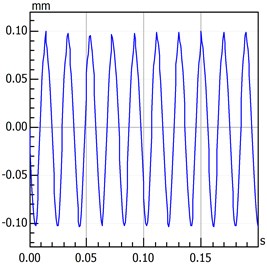
b) Time-domain waveform

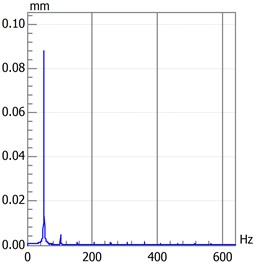
c) Spectrogram

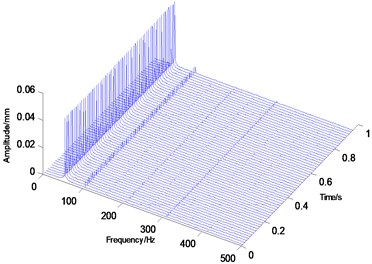
d) Waterfall

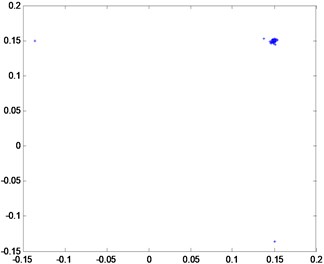
e) Poincaré map

Fig. 5Analysis result map of original data

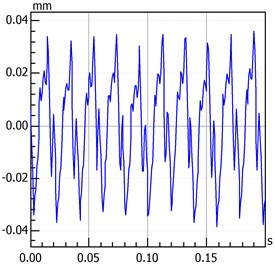
a) Time-domain waveform

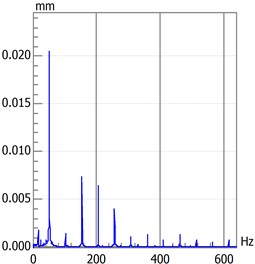
b) Spectrogram

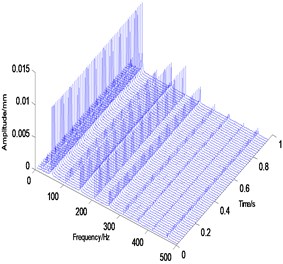
c) Waterfall

Fig. 6Analysis result map after five-layer wavelet processing

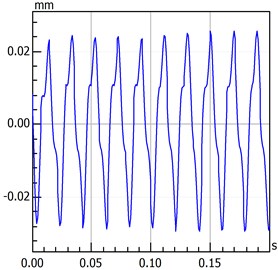
a) Time-domain waveform

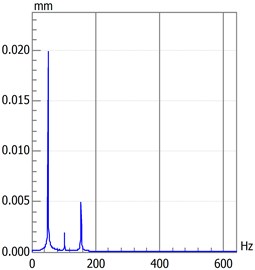
b) Spectrogram

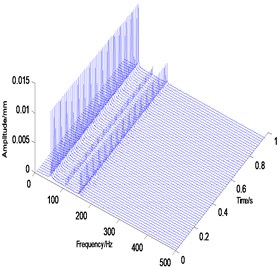
c) Waterfall

Fig. 7Analysis result map after six-layer wavelet processing

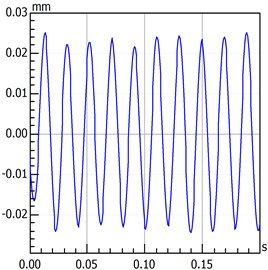
a) Time-domain waveform

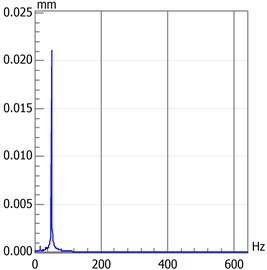
b) Spectrogram

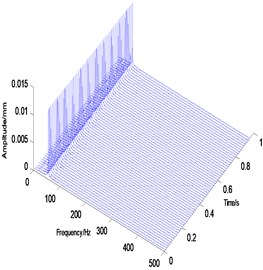
c) Waterfall

This study considers the thermal stress in the entire model. The rotor-bearing component of a gas turbine is constantly exposed to high temperatures; thus, the rotor-bearing-seal system is influenced by thermal stress. Therefore, in this paper, thermal stress is added to the right of the motion equation to analyze the influence of high temperatures on the system and find out which force of the rotor-bearing seal system is based on a steady-state temperature field. For simplification, the temperature field is assumed to be steady, and the size of the thermal stress is proportional to the temperature difference. Fig. 8 presents two-time domain waveform figures which only differ in temperatures. Comparing the contents of Fig. 8, results showed that vibration value increases as temperatures rise. Rising temperatures increase the rotor amplitude, pushing it to enter into the unstable region more quickly.

With the increased speed of the rotating shaft, the oil film vortex begins to appear and will remain until the first critical speed is increased. When the rotational speed is increased, the energy of the power frequency vibration is transferred to the oil film. When the speed becomes twice higher than the first critical speed, oil film oscillation occurs, and the vibration amplitude rapidly increases at this time.

After the analysis of the whole equation of motion, findings show that the system instability will occur in advance. The temperature rise affects the material performance, thereby reducing the stiffness of the rotor, bearing and other parts. Critical speed and shaft stiffness are proportional to the increase in temperature. Therefore, the instability of the rotor-bearing-seal system depends on the temperature increase. In the disc motion equation, the displacement of the rotor in the direction of $x$ and $y$ is larger than that of the sealing force when the sealing force is not considered. Therefore, the sealing force improves rotor system stability. Rotational speed, disc eccentricity, and seal clearance also significantly influence the rotor-bearing-seal system.

Fig. 8Time-domain waveform with different temperature

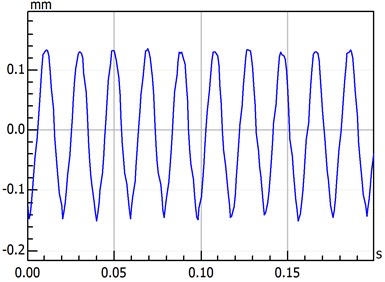
a) Low temperature

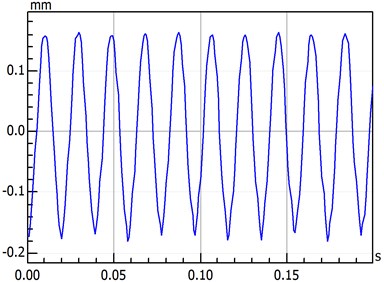
b) High temperature

4. Conclusions

1) The dynamic equations of the high-temperature rotor-bearing-seal coupled system are established and analyzed. The level of thermal force increases the instability region. The dynamic behavior of the system becomes more complicated when the thermal stress is considered. Moreover, nonlinear and experimental investigations are conducted intensively based on this model in this paper.

2) The observation of the nonlinear research demonstrates that in the Poincaré diagrams, the quasi-periodic motion occurs at a relatively high rotating speed, which is caused by the oil force. Moreover, the degree of confusion of the system decrease as the rotating speed increase, which shows that it contributes to reduce the oil whirl.

3) Based on wavelet, the quasi wavelet method is proposed. Quasi wavelet transform is a time-frequency analysis method based on convolution filter for similar wavelet analysis. The truncation error not appear in the analysis of the arbitrary waveform (except for the most extreme waveform) of the large capacity data.

4) The experimental analysis indicates that the response of rotor-bearing system is influenced by the environment temperature. The vibration amplitude decreases when the environment temperature gets down and rises up when the rotating speed increases. According to the analysis results, the correctness of theoretical model was verified.

References

Muszynska A. Model testing of rotor/bearing system. The International Journal of Analytical and Experimental Model, Vol. 1, Issue 3, 1986, p. 15-34.

Search CrossRef
Muszynska A., Bently D. E. Frequency- swept rotaing input perturbation technique s and identification of the fluid force models in rotor/bearing/seal system sand fluid handling machines. Journal of Sound and Vibration, Vol. 143, Issue 1, 1990, p. 103-124.

Publisher
Yushu C., Qian D., Shujun H. Stability and Hopf bifurcation of nonlinear rotor-seal system. Journal of Vibration Engineering, Vol. 3, 1997, p. 122-128.

Search CrossRef
Qian D., Yushu C. The harmonic resonance instability mechanism research of nonlinear rotor-seal system. Journal of Vibration Engineering, Vol. 4, 1997, p. 12-20.

Search CrossRef
Qian D., Cooper J. E., Leung A. Y. T. Hopf bifurcation analysis of a rotor/seal system. Journal of Sound and Vibration, Vol. 252, Issue 5, 2002, p. 817-833.

Publisher
Songtao L., Qinyu X., Fangyi W. Nonlinear dynamic stability research of labyrinth rotor system. Chinese Journal of Applied Mechanics, Vol. 2, 2002, p. 27-30.

Search CrossRef
Songtao L., Qinyu X., Fangyi W., et al. Stability and bifurcation of labyrinth and imbalance rotor system. Application Mathematics and Mechanics, Vol. 24, Issue 11, 2003, p. 1141-1150.

Publisher
Songtao L., Qinyu X., Xiaolong Z. Nonlinear dynamic behaviors of a rotor-labyrinth seal system. Nonlinear Dynamics, Vol. 47, Issue 4, 2007, p. 321-329.

Publisher
Chenchi W.,Herterng Y. Bifurcation analysis of bearing number in ultra-short gas bearing system. Smart Science, Vol. 1, Issue 1, 2013, p. 18-24.

Publisher
Chenchi W.,Juipin H. Theoretical and Bifurcation Analysis of a Flexible Rotor Supported by Gas-Lubricated Bearing System with Porous Bushing. Journal of Vibroengineering, Vol. 18, Issue 3, 2016, p. 1934-1940.

Publisher
Hongjun H., Jianping J. Dynamics modeling study of nonlinear rotor-seal system. Journal of Vibration and Shock, Vol. 10, 2014, p. 73-76.

Search CrossRef
Yan X., He K., Li J., et al. Numerical techniques for computing nonlinear dynamic characteristic of rotor-seal system. Journal of Mechanical Science and Technology, Vol. 28, Issue 5, 2014, p. 1727-1740.

Publisher
Jianping J., Guang M., Yi S., et al. On the oil-whipping of a rotor-bearing system by a continuum model. Applied Mathematical Modelling, Vol. 29, Issue 5, 2005, p. 461-475.

Publisher
Castro H F., Cavalca K L., Nordmann R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. Journal of Sound and Vibration, Vol. 317, Issues 1-2, 2008, p. 273-293.

Publisher
Shuxiang L., Ying C., Wenhu H., et al. Linear and nonlinear oil-film force model of rotor vibration stability. Turbine Technology, Vol. 45, Issues 5-2003, 298, p. 300-315.

Search CrossRef
Wenming Z., Jianbin Z., Guang M. Performance and stability analysis of gas-lubricated journal bearings in MEMS. Tribology International, Vol. 44, Issues 7-8, 2011, p. 887-897.

Publisher
Riemann B., Araujo Perini E., Lucchesi Cavalca K., et al. Oil whip instability control using μ-synthesis technique on a magnetic actuator. Journal of Sound and Vibration, Vol. 332, Issue 4, 2013, p. 654-673.

Publisher
Lihua Y., Weimin W., Shiquan Z., et al. A new nonlinear dynamic analysis method of rotor system supported by oil-film journal bearings. Applied Mathematical Modelling. Vol. 38, Issue 21-22, 2014, p. 5239-5255.

Publisher
Hui M., Xueling W., Heqiang N., et al. Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment. Archive of Applied Mechanics, Vol. 85, Issue 7, 2015, p. 893-907.

Publisher
Sudhakar G. N. D. S., Sekhar A. S. Identification of unbalance in a rotor bearing system. Journal of Sound and Vibration, Vol. 330, Issue 10, 2011, p. 2299-2313.

Publisher
Dakel M., Baguet S., Dufour R. Nonlinear dynamics of a support-excited flexible rotor with hydrodynamic journal bearings. Journal of Sound and Vibration, Vol. 333, Issue 10, 2014, p. 2774-2799.

Publisher
Mei C., Guang M., Jianping J. Dynamic analysis of nonlinear rotor-bearing-seal system. Journal of Vibration Engineering, Vol. 4, 2006, p. 519-524.

Search CrossRef
Mei C., Jianping J., Guang M. Nonlinear dynamic analysis of rotor-bearing-seal system. Journal of Vibration and Shock, Vol. 5, 2006, p. 171-174.

Search CrossRef
Mei C., Guang M., Jianping J. Nonlinear vibration character of rotor-bearing-seal system. Journal of Shanghai Jiaotong University, Vol. 41, Issue 3, 2007, p. 398-403.

Search CrossRef
Yanming L., Hanhua Z., Shidong F., et al. Nonlinear vibration character of rotor-bearing-seal coupled system. Lubrication Engineering, Vol. 34, Issues 1-2009, 32, p. 35-66.

Search CrossRef
Xiaoyao S., Mei Z. Nonlinear dynamics theory and experimental research of rotor-bearing-seal system. Noise and Vibration Control, Vol. 29, Issue 6, 2009, p. 67-71.

Search CrossRef
Mei C., Guang M., Jianping J. Non-linear dynamics of a rotor-bearing-seal system. Archive of Applied Mechanics, Vol. 76, Issues 3-4, 2006, p. 215-227.

Publisher
Xiaoyao S., Jia J., Mei Z., et al. Experimental and numerical analysis of nonlinear dynamics of rotor-bearing-seal system. Nonlinear Dynamics, Vol. 53, Issues 1-2, 2008, p. 31-44.

Publisher
Hui M., Hui L., Bangchun W., et al. Nonlinear dynamic analysis of a rotor-bearing-seal system under two loading conditions. Journal of Sound and Vibration, Vol. 332, Issue 23, 2013, p. 6128-6154.

Publisher
Wensheng M., Hai H. Nonlinear dynamics research of rotor-bearing-seal system. Noise and Vibration Control, Vol. 4, 2014, p. 92-95.

Search CrossRef
Xiangzhe Z., Huiqun Y., Wei H. The influence of the steady temperature field upon the critical speed of rotor system. Journal of Vibration and Shock, Vol. 12, 2007, p. 113-116.

Search CrossRef
Xiangzhe Z., Huiqun Y., Lianxiang Z. The steady state thermal vibration characteristic research of steam turbine rotor system. Power Engineering, Vol. 3, 2008, p. 377-380.

Search CrossRef
Xiangzhe Z., Wei H., Huiqun Y. The influence of steady temperature field upon the vibration characteristics of rotor system. Journal of Northeastern University (Natural Science), Vol. 1, 2008, p. 113-116.

Search CrossRef
Adiletat G., Guido A. R., Rossi C. Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dynamics, Vol. 10, Issue 6, 1996, p. 251-269.

Publisher
Childs D. W. Dynamic analysis of turbulent annular seals based on Hirs’lubrication equation. Journal of Lubrication Technology, Vol. 105, 1983, p. 429-439.

Publisher

Cited by

Simulation method for dynamic characteristics of rotor-support system subjected to environmental loads

Fengguang Xiang | Xi Chen | Dezhi Yang | Guangming Ren | Xiaohua Gan

(2024)

Integrated Computer Technologies in Mechanical Engineering - 2021

Lyudmyla Rozova | Gennadii Martynenko

(2022)

Dynamic behavior of self-acting gas-lubricated long journal bearing

Chandan Kumar | Somnath Sarangi

(2022)

Rub-impact behaviors of a multistage bladed drum rotor under high time-varying temperature

(2022)

About this article

Received

01 August 2016

Accepted

27 September 2016

Published

15 February 2017

SUBJECTS

Chaos, nonlinear dynamics and applications

DOI

https://doi.org/10.21595/jve.2016.17491

Keywords

gas turbine

rotor-bearing-seal

Poincaré

nonlinear

coupled system

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 11502140) and the “Innovation Action Program” for the Local Colleges and Universities of Capacity Building Projects in 2015 (Grant No. 15110501000).

Author Contributions

Conceived and designed the experiments and Mathematical model: Rui Zhu. Analyzed the experimental data: Yanru Zhang. Contributed analysis tools: Jianxing Ren. Responsible for guiding and modifying the thesis: Hongguang Li and Qingkai.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 08 25

Nonlinear dynamic characteristics analysis of a rotor system supported on aerodynamic bearings

Yao Fu, Fei Wang

Review article

2021 12 02

Vibration characteristics of a rotor-bearing system caused due to coupling misalignment – a review

Ashutosh Kumar, Prabhakar Sathujoda, Vinayak Ranjan

Research article

2018 08 15

Dynamic response analysis for the aero-engine dual-rotor-bearing system with flexible coupling misalignment faults

Zhenyong Lu, Xiaodong Wang, Lei Hou, Yushu Chen, Hongliang Li

Research article

2017 03 31

Study on the nonlinear transient response for the non-contact mechanical face seal

Yao Chen, Guoyuan Zhang, Weigang Zhao, Feng Ji

R. Zhu, Y. Zhang, J. Ren, H. Li, and Q. Han, “Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine,” Journal of Vibroengineering, Vol. 19, No. 1, pp. 629–640, Feb. 2017, https://doi.org/10.21595/jve.2016.17491

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17491
UR  - https://doi.org/10.21595/jve.2016.17491
TI  - Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine
T2  - Journal of Vibroengineering
AU  - Zhu, Rui
AU  - Zhang, Yanru
AU  - Ren, Jianxing
AU  - Li, Hongguang
AU  - Han, Qingkai
PY  - 2017
DA  - 2017/02/15
PB  - JVE International Ltd.
SP  - 629-640
IS  - 1
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhu_2017,
	doi = {10.21595/jve.2016.17491},
	url = {https://doi.org/10.21595/jve.2016.17491},
	year = 2017,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {1},
	pages = {629--640},
	author = {Rui Zhu and Yanru Zhang and Jianxing Ren and Hongguang Li and Qingkai Han},
	title = {Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]R. Zhu, Y. Zhang, J. Ren, H. Li, and Q. Han, “Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine,” Journal of Vibroengineering, vol. 19, no. 1, pp. 629–640, Feb. 2017, doi: 10.21595/jve.2016.17491.

Copy IEEE

Copied to clipboard!

Zhu, Rui, Yanru Zhang, Jianxing Ren, Hongguang Li, and Qingkai Han. “Nonlinear Dynamics Study of a High-Temperature Rotor-Bearing-Seal System in Gas Turbine.” Journal of Vibroengineering 19, no. 1 (February 15, 2017): 629–40. https://doi.org/10.21595/jve.2016.17491.

Copy Chicago

Copied to clipboard!

Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine

Abstract

1. Introduction

2. Mathematical model of a rotor-bearing-seal system with two discs

2.1. Equation of motion

2.2. Nonlinear oil-film force and thermal stress

2.3. Nonlinear seal force

3. Analysis of experimental results

4. Conclusions

References

Cited by

About this article

Related Articles