The dynamics of a nonautonomous oscillator with friction memory

1.1. Mathematical model

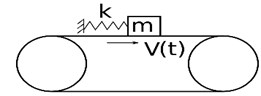
The model considered in this article is depicted in Fig. 1(a).

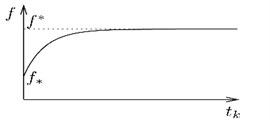
Fig. 1Physical model of a vibration system

a)

b)

The model consists of a mass $m$, that rides on a moving belt with dry friction. The belt moves with periodically changing velocity $V\left(t\right)$. The mass is attached to inertial space by a spring with stiffness $k$. The coefficient of static friction, in accordance with the hypothesis of Ishlinskiyi A. Yi., Kragelskiyi I. V. [1], is considered to be a continuous monotonically increasing function of the time $t_k$ of stationary contact (stick motion of the mass and the belt) as depicted in Fig. 1(b). The Coulomb model is used for non-static dry friction.

The motion of the mass in the model is described by the Eq. (1), (2):

Eq. (1) describes the slip motion of the mass with non-static dry friction with coefficient $f_{*}$_. Eq. (2) describes the condition for the stick motion. $f_{\mathrm{п}}\left(t_k\right)$ is the coefficient of static friction as a function of the stick motion time $t_k$. Note that when $V\left(t\right)=const$, the Eq. (1) takes the form of the corresponding equation in [4].

With dimensionless time $\tau =t{\omega }_0$, coordinate $\xi =xk/f_{\mathrm{*}}P$ and parameters ${\omega }_0=\sqrt{k/m}$, $\theta \left(\tau \right)=V\sqrt{km}/f_{\mathrm{*}}P$, the Eq. (1), (2) will take the form:

where $\epsilon \left({\tau }_k\right)=(f_{\mathrm{п}}\left({\tau }_k\right)-f_{\mathrm{*}}){f_{\mathrm{*}}}^{-1}$ – dimensionless coefficient of static friction).

1.2. Structure of the phase space

Since the system is non-autonomous and can be described by second-order differential equation, its state is a triplet $\left\{\xi ,\dot{\xi },\tau \right\}$ (Fig. 2), and its phase space is accordingly 3-dimensional. The phase space is split into 2 half-spaces ${\mathrm{\Phi }}_1(\xi ,\dot{\xi }>\theta ,\tau )$ and ${\mathrm{\Phi }}_2(\xi ,\dot{\xi }<\theta ,\tau )$ by the surface $\mathrm{\Pi }\left(\dot{\xi }=\theta \left(\tau \right)\right)$.

The shape of phase trajectories in each half-space is described by the Eq. (5), (6):

It can be shown, that on the surface $П$ there is a strip of stick motions ${\mathrm{П}}_C$ bounded by curves ${\mathrm{Г}}_1$ and ${\mathrm{Г}}_2$:

On the strip ${\mathrm{П}}_C$ a phase trajectory is described by Eq. (8):

An example of a phase space trajectory with stick motion intervals is shown in Fig. 3.

Fig. 2Phase space S

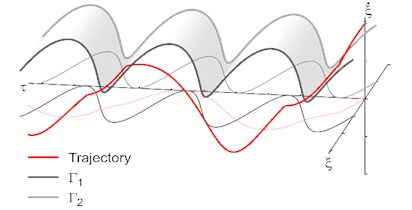
Fig. 3The qualitative form of the phase trajectories

1.3. Dynamics of the system

For the purpose of modeling the dynamics of system Eqs. (1-2), the function for the dimensionless belt speed was taken as follows: $\theta \left(\tau \right)=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{\Omega }\tau \right)+B$. The function $\epsilon \left({\tau }_k\right)$ for the dimensionless coefficient of static friction was taken as follows:

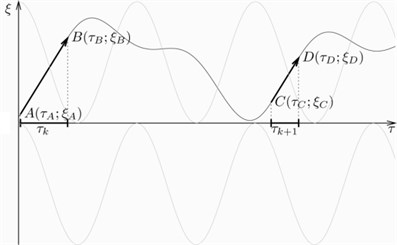
Suppose $M_i\left({\tau }_i,{\xi }_i\right)$, $i=\mathrm{0,1},..,n$ – a sequence of point on the surface $П$, which does not belong to the strip ${\mathrm{П}}_C$ and which is determined by the Eq. (5) for $i=2k<n$, $k=$ 1, 2,… and Eq. (6) for $i=2m+1<n$, $m=\mathrm{}$0, 1,…. Suppose as well, that the coordinates of $M_0$ are $\tau ={\tau }_0$, $\xi =1+\epsilon \left({\tau }_{k,c}\right)$, $\dot{\xi }=\theta \left({\tau }_0\right)$. For such sequence, a number n can be found, for which $M_{n+1}\left({\tau }_p,{\xi }_p\right)$ will belong to the strip ${\mathrm{П}}_C$ and the interval of phase trajectory is described by Eq. (9) until the point determined from condition Eq. (4). Let’s take ${{\rm T}}_{+}$ to denote the mapping $M_{2k+1}\to M_{2k+2}$, $k=\text{0,}\text{1,}\text{2,}\text{…}<n$, and ${{\rm T}}_{-}$ – the mapping $M_{2m}\to M_{2m+1}$, $m=\text{1,}\text{2,}\text{…}<n$ . The mapping $M_0\to M_{n+1}$ can thus be described by ${{\rm T}}_1\left(j,l,n\right)={\left({\left({{\rm T}}_{-}\right)}^j{\left({{\rm T}}_{+}\right)}^l\right)}^{\left[\frac{n}{2}\right]}$, $l$, $j=\mathrm{}$0, 1,..., $n$. The connection between two adjacent stick motion intervals ${\tau }_k$, ${\tau }_{k+1}$ can be described as follows $\psi \left({\tau }_{k+1}\right)=\phi \left({\tau }_k\right)$:

Since the system state trajectory will always end on the sliding surface, they dynamics of the system can be examined using Poincare map of the boundary ${\mathrm{Г}}_1\left({\mathrm{Г}}_2\right)$ into itself, or using the sequence of durations of stick motions ${\tau }_k$, $k=\mathrm{}$1, 2, 3… To study the dynamics of the system, we developed an application allowing to perform calculations of trajectories of the system, the Poincare maps, and bifurcation diagrams, using different values of the system parameters. All calculations are done using double precision floating point arithmetic. When calculating a single trajectory, different points on the trajectory are calculated with progressively increasing time distance from the initial point, until the trajectory reaches a boundary between areas where the system behavior is described by different equations, e.g. when the trajectory reaches the surface $\mathrm{\Pi }\left(\dot{\xi }=\theta \left(\tau \right)\right)$. Then the accuracy of the calculated point of the transition to a different area is further improved using bisection method, until the desired accuracy is reached. After that, a new trajectory piece is calculated the same way starting from the calculated transition point as the initial point. Trajectory pieces are calculated until the time or the number of stick motion interval reaches the defined limit.

To build a bifurcation diagram, one of the parameters is selected to be varied and its range is selected. Then for each value in the range its own trajectory is calculated, with all the other parameters having the same values for each trajectory. To build the graph, a certain number (usually 30) of last intervals of stick motion are taken and displayed for each trajectory.

1.4. The results of numerical calculations

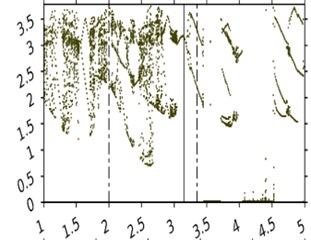
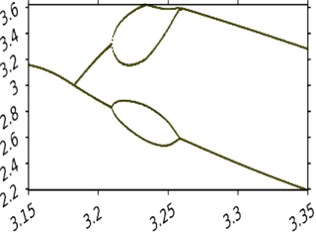
Fig. 4 displays a bifurcation diagram with $\mathrm{\Omega }$ as the variable parameter. The other parameters’ values are: $\theta \left(\tau \right)=0.1\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{\Omega }\tau \right)+1.41$, ${\epsilon }_{*}=\text{3}.$ Fig. 5(a) displays a diagram with parameter $\Omega$ range from 1 to 5, the other subfigures show different subintervals of that.

Fig. 4 shows that depending on the frequency of the belt movement, the system can display different types of dynamic behavior, including chaos. It should be noted, that with the increase of the frequency chaos become less frequent.

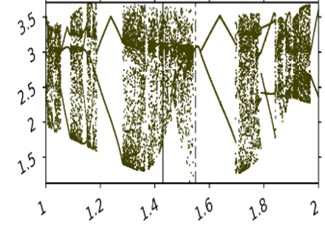
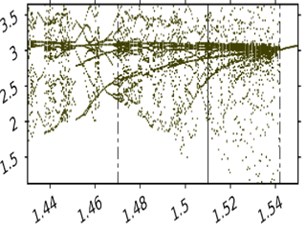
Fig. 5 displays diagrams with $A$ as the variable parameter and $\theta \left(\tau \right)=A\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{\Omega }\tau \right)+1.41$, ${\epsilon }_{\mathrm{*}}=\mathrm{}$3. $\mathrm{\Omega }=\mathrm{}$1.466 on Fig. 5(a) and $\mathrm{\Omega }=\mathrm{}$3.23 on Fig. 5(b).

Fig. 5 shows the influence of the increase of the amplitude of the belt oscillations on the dynamics of the system. Two conclusions can be made based on it. One, the increase of the amplitude from zero and within a small vicinity of zero changes the dynamics of the system gradually, without sudden qualitative changes.

Fig. 4Bifurcation diagrams in frequency Ω tape oscillation

a)

b)

c)

d)

Fig. 5The bifurcation diagram of the amplitude A fluctuations tape

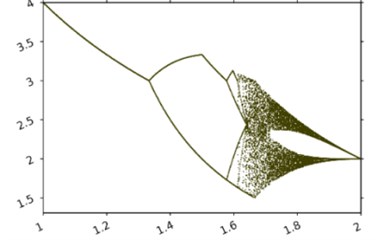
a)

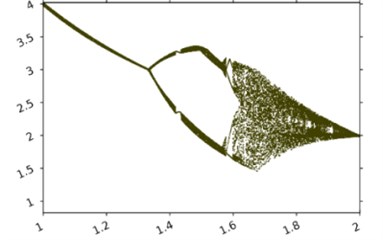
b)