Bifurcation and chaos analysis of a gear pair system with multi-clearance

2.1. Model of the gear pair system

A spur gear pair consists of pinion, gear, shafts and bearings. In order to build the dynamic model conveniently and effectively, pinion and gear are modeled as rigid body. Meantime, the shafts and bearings supported the gears are assumed to equivalent elements with viscous damping coefficient and equivalent supported stiffness [17]. Based on the centralized mass method, the nonlinear dynamic model of the gear set is shown in Fig. 1. In the system, the static transmission error, gear backlash, bearing clearance, time-varying meshing stiffness, torque fluctuation, external radial preload, and so forth, are taken into consideration. In addition, teeth modification, profile shifting and friction are neglected in the model.

Fig. 1Nonlinear dynamic model of a spur gear pair system

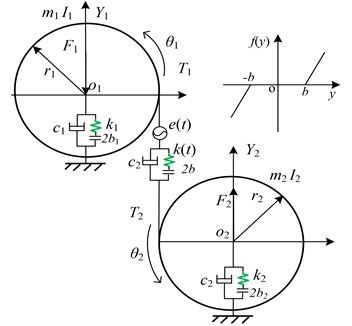
In Fig. 1, it is assumed that the meshing line direction between the two gears is defined as $Y$ direction of the coordinate system in the gear pair model. Each gear considers a translational degree of freedom ($Y$) and a rotational degree of freedom ($\theta$). Here, $m_1$ and $m_2$ mean the equivalent masses of the two gears, respectively; $r_1$ and $r_2$ represent the radius of base circles of the two gears, respectively; $I_1$ and $I_2$ show the moment of inertia of the two gears, respectively; $k_i$, $c_i$ and 2$b_i$ ($i=$ 1, 2) refer to the equivalent support stiffness, the equivalent support damping and bearing clearance of the two gears, respectively. $k\left(t\right)$ and $c_m$ are the time-varying meshing stiffness and damping between the two gears, respectively. $2b$ represents the gear meshing backlash. $F_1$ and $F_2$ are the external radial preload sustained by bearings. Additionally, $T_1$ and $T_2$ are the input torque and output torque impacting on driving gear and driven gear, respectively. Torque $T_i$ ($i=$ 1, 2) are composed of mean torque $T_{im}$ and fluctuation value $T_{ia}$. Therefore, torque $T_i$ can be expressed as follows:

As shown in Fig. 1, the gear system has four degrees of freedom including two translational degrees of freedom ($Y_{o1}$, $Y_{o2}$) and two torsional degrees of freedom (${\theta }_1$, ${\theta }_2$). When the relative displacement caused by torsional vibration in the gear pair system is $Y_{or}$, $Y_{or}$ can be described as:

where $e\left(t\right)=\sum _{r=1}^{\infty }{e}_r\mathrm{s}\mathrm{i}\mathrm{n}(r\omega t+{\phi }_r)$ is the static transmission error of the gear pair system, in which $e_r$ is the fluctuation value and ${\phi }_r$ represents the initial phase of error.

When the gear backlash between the driven gear and driving gear is 2$b$, the elastic restoring force $F_k$ can be represented by:

where $k\left(t\right)$ is the time-varying meshing stiffness, and $f\left(Y_{or},b\right)$ is the nonlinear backlash function which can be written as:

With the purpose of ensuring the smoothness of gear transmission, the contact ratio of gear pair system is usually under the range of 1 to 2. In other words, the number of tooth pairs will always alternate between one and two in the process of continuous meshing, leading to the generation of dynamic excitation force, where the meshing stiffness shows time-varying property. Thus, the time-varying meshing stiffness can be expressed in Fourier series expansion method as follows:

where $k_m$ is the mean meshing stiffness and $\omega$ is the meshing fundamental frequency. Additionally, $a_n$ and $b_n$ are the expansion coefficient of Fourier series, respectively.

The damping force is defined as:

where $c_m$ is the meshing damping, which can be given as:

where $\xi$ is the damping ratio ($\xi =$ 0.03-0.17).

Hence, the dynamics meshing loads $F$ can be expressed as:

2.2. Dynamic differential equations

In terms of the analysis above, the nonlinear dynamic differential equation of a spur gear pair system can be established by using Newton’s second law of motion as follows:

where $f_1\left(Y_{o1},b_1\right)$ and $f_2\left(Y_{o2},b_2\right)$ are the radical clearances displacement function along $Y_{or}$ direction respectively, which could be expressed as:

However, the above gear pair is a semi-definite system that has rigid body displacement, owing to gear backlash and bearing clearance. It means that the motion equations of the gear system cannot be directly solved by numerical integration method. A new relative coordinate $Y_o$ is thus introduced to reduce the dimension of dynamic equation, which will make the equation solvable [21]. As a new degree of freedom, the relative coordinate $Y_o$ can be defined as follows:

Therefore, the Eq. (9) can be transferred by substituting the relative coordinate $Y_o$ to the following expression:

where $m_e$ and $F_m$ are equivalent mass of the gear pair and the average force related to mean torque respectively, with $m_e=I_1{I}_2/\left(I_1{r}_1^2+I_2{r}_2^2\right)$ and $F_m=T_{1m}/r_1=T_{2m}/r_2$.

2.3. Dimensionless equations of motion

In order to compare and analyze the results under the same dimensional scale [21], it is intensely indispensable to make motion equations of gear system dimensionless. Thus, dimensionless time parameter $\tau$ introduced can be defined as $\tau ={\omega }_{n}t$ with ${\omega }_n=\sqrt{k_m/m_e}$, where ${\omega }_n$ is natural frequency of the gear pair system. Meanwhile, displacement of nominal dimension $b_c$ is introduced as well. Then, others parameters, such as displacement, velocity and acceleration could be described by $\tau$ and $b_c$ as follows:

Dimensionless nonlinear clearance function can then be rewritten as:

where $B=b/b_c$ and $B_i=b_i/b_c$ ($i=$ 1, 2).

Substituting the dimensionless parameters above into Eq. (12) and then dimensionless equation of motion can be expressed as matrix form:

where $\mathbf{M}$ is the mass matrix, $\mathbf{K}$ represents the stiffness matrix, $\mathbf{C}$ refers to the damping matrix, $\mathbf{F}$ is the force vector and $\mathbf{X}$ is the displacement vector. The matrix and vector can be expressed as follows:

where:

3.1. Bifurcation and chaos analysis of the effect of dimensionless meshing frequency

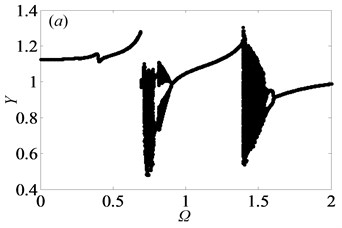
In gear transmission system, meshing frequency is one of important factors which have an important effect on the dynamic response of system. In order to obtain the bifurcation diagrams with the change of dimensionless meshing frequency $\mathrm{\Omega }$, some parameters in the gear system are selected as follows: $\mathrm{\Delta }=$ 0.5 or 2, i.e. the gear system is under the lightly loaded condition or under the heavily loaded condition [1], $f_1=f_2=$0.15, $B_1=B_2=$ 0.25, $B=$ 1. The bifurcation properties of the gear system with $\mathrm{\Omega }$ varying are firstly analyzed with $\mathrm{\Delta }=$ 0.5. Then, Fig. 2 shows the bifurcation diagrams of $\mathrm{\Omega }$ with respect to $Y$ under lightly loaded condition, when the damping ratio $\xi$ is equal to 0.03, 0.05, 0.07 and 0.09, respectively. It can be seen from the figure that the gear system presents complex motion states including periodic, quasi-periodic and chaotic motions with the change of $\mathrm{\Omega }$ and $\xi$.

When damping ratio $\xi =$ 0.03, the gear system mainly indicates in the motion state of period-one and chaos with the range of 0 $\le \mathrm{\Omega }\le$ 2 in Fig. 2(a). At the initial value of $\mathrm{\Omega }$, the system undergoes period-one motion, and then bifurcates into period-two motion by the way of crisis. Subsequently, the system motion state becomes chaotic, in which these motion states of gear system within the range of 0.5 $\le \mathrm{\Omega }\le$ 0.7 will be further described in detail as shown in Figs. 3-4. Besides, between two chaotic regions, the system goes through an exceedingly short zone of period motion. Furthermore, the bifurcation diagrams in Fig. 2 reveal significant variations that the window width of the regions of chaotic state decreases notably as damping ratio $\xi$ increases from 0.03 to 0.09. It means that chaotic behavior can be hindered when $\xi$ increases, whereas high damping will make the system consume more energy. This is in agreement with the analysis results on a spur gear pair system [1] and the planetary gear train [22]. Obviously, when $\xi$ is 0.09, chaotic motion is almost replaced by quasi-periodic and period-doubling motions at the first part of chaos regions, as shown in Fig. 2(d).

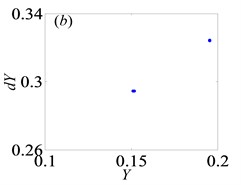
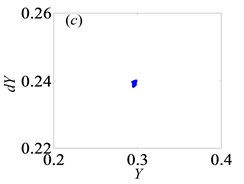
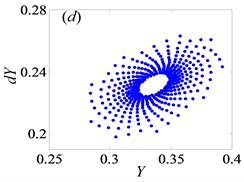
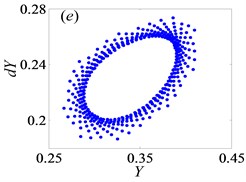
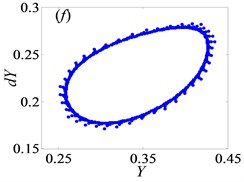
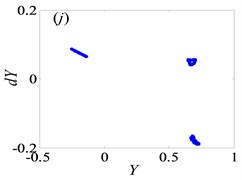
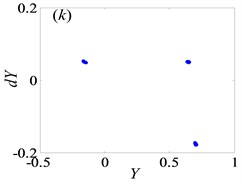
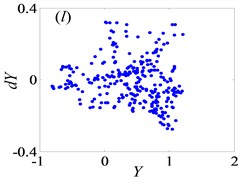
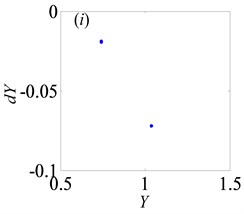
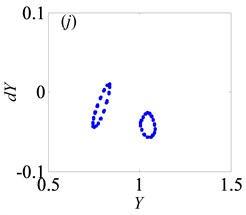
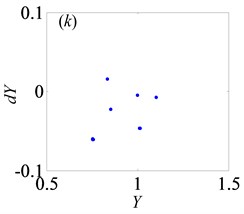
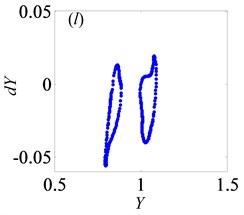
For the purpose of demonstrating the detailed transformational process concerning motion states of gear system with the change of $\mathrm{\Omega }$, Poincaré maps of $Y$ with respect to $dY$ are applied to represent the dynamic characteristics of the gear pair system in Figs. 4(a)-(l). Then, Fig. 3 exhibits that the bifurcation diagram within the range of 0.5 $\le \mathrm{\Omega }\le \mathrm{}$0.7 is taken as an example to illustrate the bifurcation behavior of gear system at length. In Fig. 3, the period motion, namely period-one and period-two, can be observed at the low values of $\mathrm{\Omega }$ (i.e. 0.5 $<\mathrm{\Omega }\mathrm{}<$ 0.611), and the corresponding Poincaré maps are shown in Figs. 4(a)-(c). When $\mathrm{\Omega }$ increases from 0.612 to 0.624, the system goes into the quasi-periodic motion which describes as seen in Figs. 4(d)-(g). However, the system response turns from quasi-periodic motion to period doubling motion with the influence of stable attractor as shown in Fig. 4(h). Subsequently, the chaos occurs by the way of period doubling motion. Before entering into next state of chaos, there is a short Hopf bifurcation and period-three motion at $\mathrm{\Omega }=$ 0.679 and $\mathrm{\Omega }=$ 0.682, respectively. A similar evolution of motion is described with the increasing of meshing frequency in Ref. [1]. However, there are other motion states including quasi-periodic and Hopf motion in the gear pair system of Fig. 1 where more degrees-of-freedom are considered in this model.

Fig. 2Under lightly loaded condition, bifurcation diagrams of Ω with respect to Y when ξ is a) 0.03, b) 0.05, c) 0.07 and d) 0.09, respectively

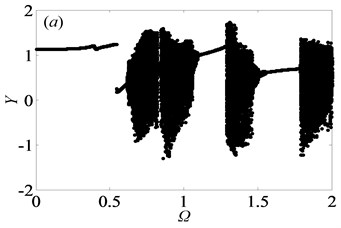
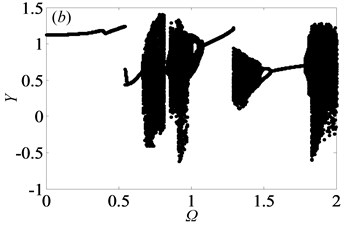
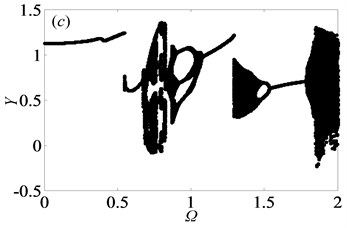
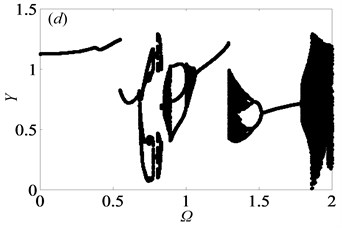
From the bifurcation diagrams in Fig. 2, it can be observed clearly that when $\mathrm{\Delta }=$ 0.5, the gear system undergoes different motion states consisting of period doubling motion, quasi-periodic motion, Hopf bifurcation and chaos as $\mathrm{\Omega }$ increases. Importantly, the chaos occupies the main motion state in Figs. 2(a)-(b), which reveals that double-sided impact exists frequently in gear system when tooth pair keeps in mesh. In other words, the system may get into chaos easily, which would lead to predict and control the motion state of the system hard.

Fig. 3Under lightly loaded condition, partial enlarged drawing of bifurcation diagram with the range of 0.5 ≤Ω≤0.7 when ξ is 0.03

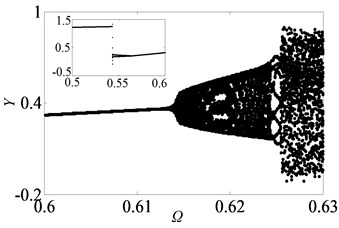
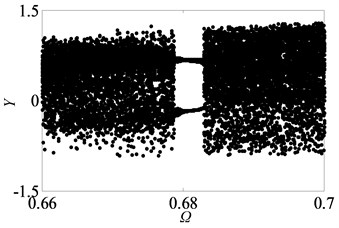
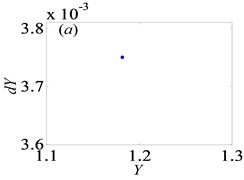
Fig. 4Under lightly loaded condition, Poincaré maps of Y with respect to dY at ξ= 0.03, when Ω is a) 0.45, b) 0.55, c) 0.6, d) 0.612, e) 0.613, f) 0.614, g) 0.618, h) 0.625, i) 0.627, j) 0.679, k) 0.682 and l) 0.686, respectively

When $\mathrm{\Delta }=$ 2, Fig. 5 shows the bifurcation diagrams of $\mathrm{\Omega }$ with respect to $Y$ at different damping ratio $\xi$ values, keeping other parameters same with those under lightly loaded condition. Comparing bifurcation diagrams in Figs. 5(a)-(d), it is observed that the width of regions of chaos state becomes narrow gradually with the increasing of $\xi$ from 0.03 to 0.09, which is quite similar to that under lightly loaded condition. When the damping is equal to 0.09, the chaos is even completely replaced by periodic motion state. The phenomenon verifies the conclusion that increasing damping narrows the region of instability [8, 9, 23]. Due to large damping, higher energy is dissipated by the power transmission where the dynamic response and stability of system are improved.

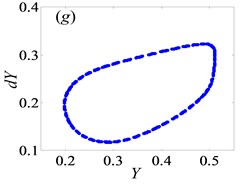
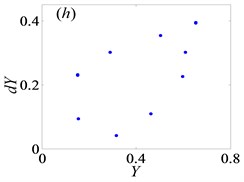
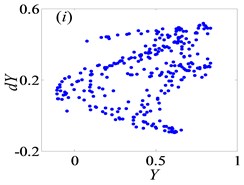
Similarly, the system goes into various types of motion state when $\mathrm{\Delta }=$ 2. To research qualitatively the nonlinear dynamic behaviors of gear system under $\mathrm{\Delta }=$ 2, it is essential to analyze bifurcation diagram with dimensionless meshing frequency $\mathrm{\Omega }$ varying, as shown in Fig. (6). Meanwhile, Fig. (7) shows the Poincaré maps of $Y$ with respect to $dY$ as $\mathrm{\Omega }$ changes from 0.65 to 0.95 at $\xi =$ 0.03, which indicate the transitional process of motion states. From these above figures, the system enters into period-one state with the range of $\mathrm{\Omega }$ from 0.65 to 0.71, then changes to chaotic motion when $\mathrm{\Omega }$ increases to 0.715, as shown in Figs. 7(a)-(b), respectively. As $\mathrm{\Omega }$ reaches to 0.719, the system bifurcates from chaos to period doubling motion. After that it goes through chaotic motion again when $\mathrm{\Omega }=$ 0.74 in Figs. 7(c)-(d). Subsequently, the system switches to period-six and period-three motions, then turns into chaos state via period doubling. After the width of region of chaotic motion, system bifurcates to period-four and period-two motion forms when $\mathrm{\Omega }$ increases to 0.774 and 0.79, respectively. Then, in the range of 0.81 $<\mathrm{\Omega }<$ 0.89, the system frequently switches Hopf motion to period doubling motion, as shown in Figs. 7(j)-(n), respectively. After that, motion state of the system undergoes period-one state when $\mathrm{\Omega }=$ 0.92. As a result, when meshing frequency varies, the system shows a diverse range of motion forms [2].

Fig. 5Under heavily loaded condition, bifurcation diagrams of Ω with respect to Y when ξ is a) 0.03, b) 0.05, c) 0.07 and d) 0.09, respectively

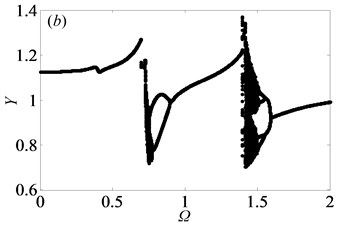
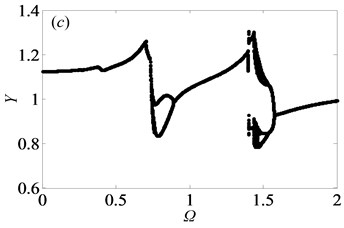
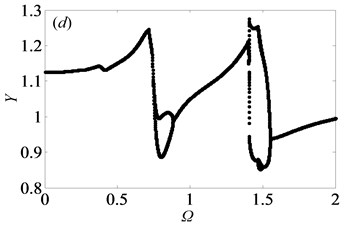
Comparing Fig. 2 and Fig. 5, it can be seen that the gear system is in the more stable state under heavily loaded condition than that under lightly loaded condition, which has been proved in Ref. [1]. To some extent, the main reason is that when the external load increases, the static meshing force will increase as well, triggering that double-sided and single-sided impact will disappear gradually to make gear pair meshing continuously. Meanwhile, it clearly shows that the system switches from chaos to period motion as illustrated in corresponding bifurcation diagrams. Furthermore, as damping ratio $\xi$ increases, the chaotic motion of system gradually transfers into quasi-periodic or period doubling motions. Through the above analysis of bifurcation features with $\mathrm{\Omega }$ changing under different loaded conditions, the motion states and the critical values can be obtained, which can apply to choose the reasonable rotational speed for keeping the stable motion state of gear system.

Fig. 6Under heavily loaded condition, partial enlarged drawing of bifurcation diagram with the range of 0.65 ≤Ω≤ 0.95 when ξ is 0.03

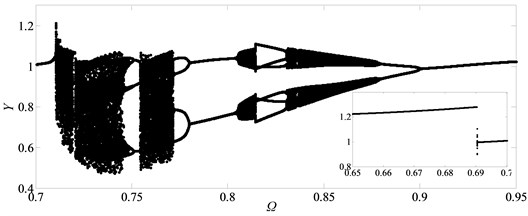
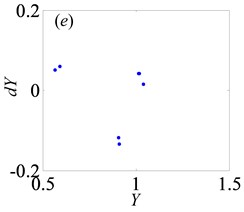
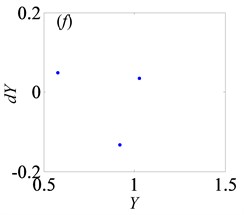
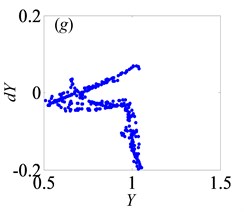
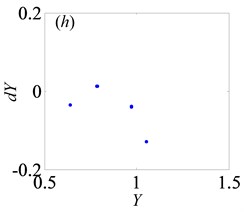
Fig. 7Under heavily loaded condition, Poincaré maps of Y with respect to dY at ξ= 0.03, when Ω is a) 0.65, b) 0.715, c) 0.719, d) 0.740, e) 0.749, f) 0.752, g) 0.76, h) 0.774, i) 0.79, j) 0.81, k) 0.82, l) 0.832, m) 0.86, n) 0.89 and o) 0.92, respectively

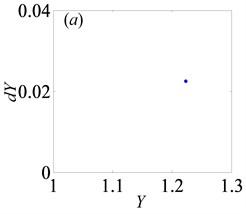
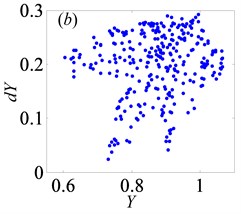
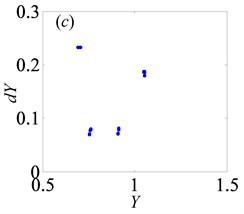
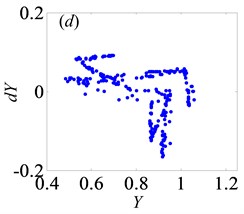
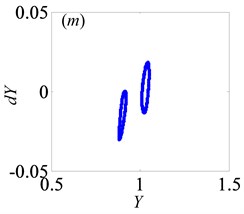
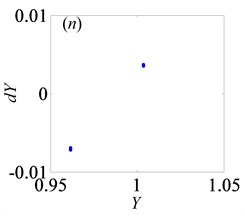
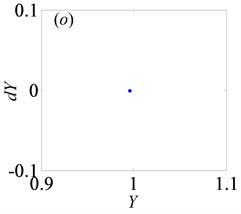
3.2. Bifurcation and chaos analysis of the effect of dimensionless gear backlash

Owing to some objective factors, namely manufacturing accuracy, installation error, gear lubrication and so on, gear backlash always exists, which shows strong nonlinear feature and has a great influence on the durability and stability of gear system [17]. Therefore, it is vital to analyze the nonlinear behaviors of gear system caused by gear backlash. Keeping other system parameters constant, the gear backlash B is assigned as control parameter.

When $\mathrm{\Delta }=$ 0.5, the bifurcation diagrams with the change of dimensionless gear backlash $B$ are shown in Fig. 8. Under lightly loaded condition, as damping ratio $\xi$ reaches to 0.03, 0.05, 0.07 and 0.09 respectively, Fig. 8 suggests the different bifurcation characteristics of the gear system. When $B$ increases from 0 to 1, the system enters into chaotic state by the way of period-three motion and then transfers frequently between chaos and period doubling motion as shown in Figs. 8(a)-(b). However, it could be shown from Figs. 8(c)-(d) that the system response starts with period-three, then undergoes chaos, finally bifurcates to period-one within the range of 0 $<B<$ 1. When $B$ continues to increase, the system goes into chaos again by the channel of period doubling or period-one motion as seen in Figs. 8(a)-(c), while it will always be under period-one motion in Fig. 8(d). As $\xi =$ 0.11, the system motion only includes period-three and period-one motions. A similar process of bifurcation with different damping ratio $\xi$ can be found in Ref. [22]. As $\xi$ increases, the width of window of chaotic motion becomes narrower gradually and the system enters into the second part of regions of chaotic motion much earlier. However, the overall area of chaotic region is gradually reduced, especially in the longitudinal direction. When $\xi$ is equal to 0.11, the second part of chaotic region disappears, which is replaced by period-one motion. Additionally, the amplitude of vibration displacement decreases gradually as $\xi$ increases, which is revealed from Ref. [1] as well.

Fig. 8Under lightly loaded condition, bifurcation diagrams of B with respect to Y when ξ is a) 0.03, b) 0.05, c) 0.07 and d) 0.09, respectively

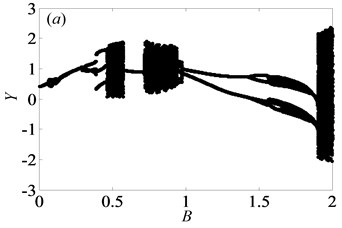
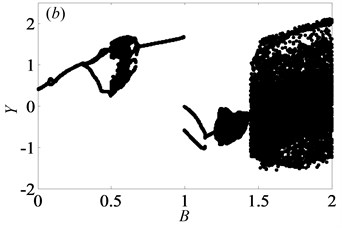
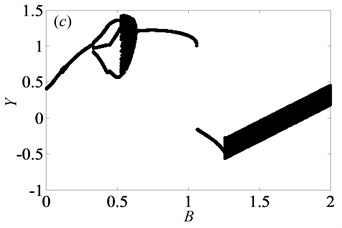
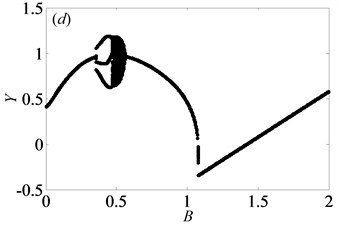
In order to further explain the change process of motion states of gear system, partial enlarged drawing of bifurcation diagram and the corresponding Poincaré maps are shown in Figs. 9-10 respectively, when $B$ is in the range from 0.05 to 0.65 and $\xi$ is 0.03. From Fig. 9, it clearly shows that the system goes into complex motion states, involving period doubling motion, quasi-periodic motion, Hopf bifurcation motion as well as chaos. When $B=$ 0.05, the system is in the period-one motion as exhibited in Fig. 10(a), which reveals that the system is under the stable state. Due to small value of gear backlash, gears keep meshing so that the system always undergoes the stable period-one motion state. Then, the system bifurcates to period-two motion as $B$ increases to 0.075.

Fig. 9Under lightly loaded condition, partial enlarged drawing of bifurcation diagram with the range of 0.05 ≤B≤ 0.65 when ξ is 0.03

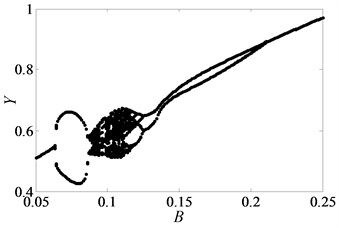
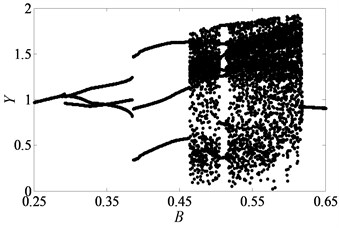
Fig. 10Under lightly loaded condition, Poincaré maps of Y with respect to dY at ξ= 0.03, when B is a) 0.05, b) 0.075, c) 0.09, d) 0.097, e) 0.103, f) 0.118, g) 0.122, h) 0.14, i) 0.35, j) 0.48, k) 0.5145, l) 0.54, respectively

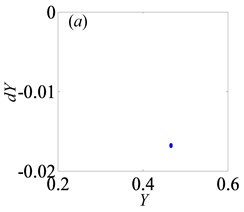
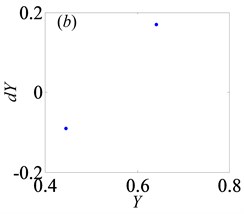
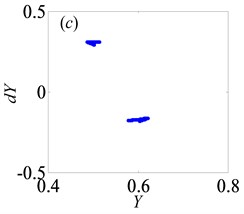
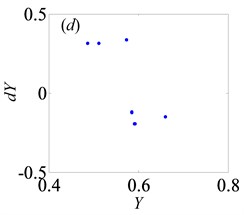
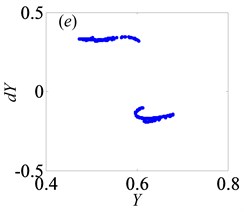
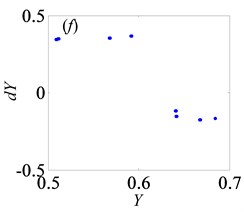
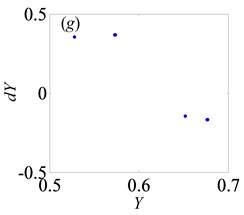
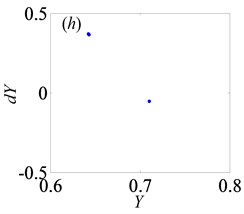
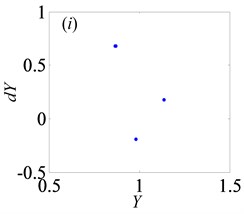
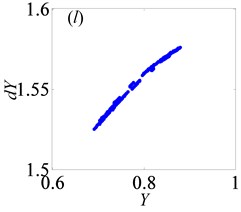
Later, the system goes into the complex states which converts frequently between chaos and period doubling motion, when $B$ changes from 0.087 to 0.118, as can be seen from Figs. 10(c)-(f). Then, the system bifurcates inversely from period-eight to period-four and even period-two, as $B$ reaches to 0.122 and 0.14, which demonstrate from Figs. 10(g)-(h), respectively. However, the system gets into period-three motion by the way of crisis from period-two motion in Fig. 10(i) when $B=$ 0.35. As $B$ continues to increase, the system switches to chaos, then changes to quasi-periodic motion, finally transfer into chaos again, as shown in Figs. 10(j)-(l).

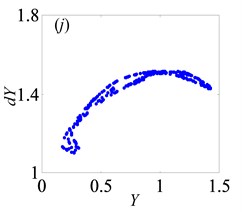
Based on the above analysis, the dimensionless gear backlash varying leads to complex bifurcation properties, which can be employed to illustrate the nonlinear dynamic characteristics of gear system. When $\mathrm{\Delta }$ is 0.5 and $\xi$ is less than or equal to 0.05, the gear system presents the states of periodic motion and chaotic motion alternately with the increase of $B$. However, when $B$ is larger than a certain value, the system enters into the continuous chaotic motion, as seen in Figs. 8(a)-(b). Likewise, it is of significance to analyze the bifurcation features under heavily loaded condition to compare those under lightly loaded condition. Hence, the system parameters are selected as same as those under lightly loaded condition. Then, the bifurcation diagram with the change of $B$ is obtained as seen in Fig. 11.

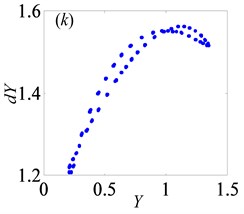
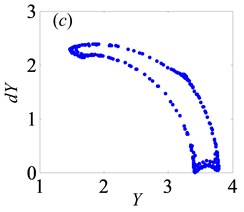
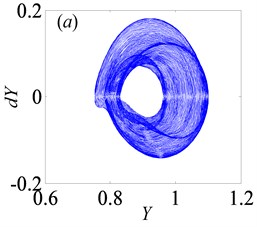
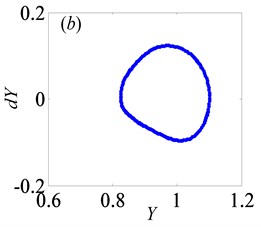
In Fig. 11, as $B$ increases from 0 to 2, the system keeps under period-one motion, and the corresponding phase portrait and Poincaré map are shown in Fig. 12, when $B=$ 0.5. In other words, gear backlash $B$ varying only changes the vibration amplitude of gear system while it doesn’t affect the system motion property. This is in line with the numerical analysis results of a spur gear pair system with three DOF described in Ref. [24].

By comparing Fig. 8 and Fig. 12, it can be seen that the influences of loaded condition, damping ratio and dimensionless gear backlash on the bifurcation characteristics of gear system are analyzed systematically. Under lightly loaded condition, the system has more complex bifurcation features than those under heavily loaded condition. Furthermore, under different damping ratios, there are significant differences among the bifurcation diagrams of $B$ with respect to $Y$. As $\xi$ increases, the system tends to enter into the stable period motion state. Hence, these analysis results can provide theoretical basis for selecting appropriate gear backlash to avoid the chaos and ensure the system under the stable motion state.

Fig. 11Under heavily loaded condition, bifurcation diagrams of B with respect to Y

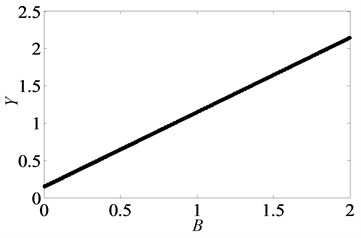
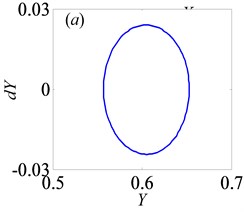
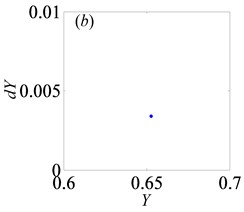
Fig. 12Under heavily loaded condition, phase portrait and Poincaré maps of Y with respect to dY when B= 0.5

3.3. Bifurcation and chaos analysis of the effect of dimensionless bearing clearance

Bearing clearance is also one of key parameters that affect the dynamic behavior of gear transmission system. Therefore, it is crucial to analyze the influence of bearing clearance on nonlinear dynamic characteristic of system. Then, keeping other parameters constant, the bifurcation diagrams with dimensionless bearing clearance $B_i$ ($i=$ 1, 2) changing are obtained when $\mathrm{\Delta }=$ 0.5 or 2, as shown in Fig. 13 and Fig. 15, respectively.

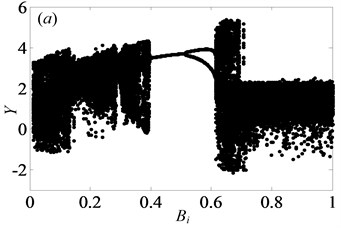
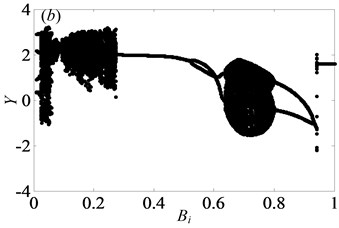
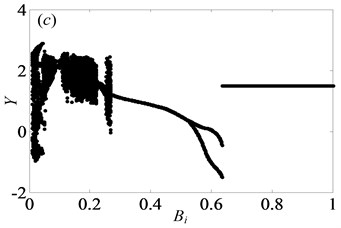
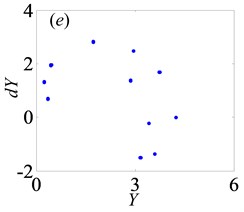
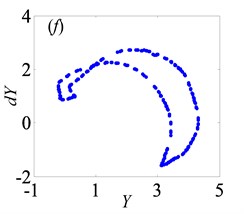
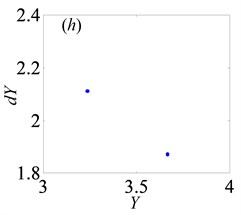
In Fig. 13, when $\mathrm{\Delta }=$ 0.5, the system shows complex forms of motion states with the change of $B_i$ and different $\xi$. From Fig. 13(a), it clearly indicates that the chaos is the main motion within the range of 0 $<B_i<$ 1, but in the meantime, there are other motion types, namely period doubling and quasi-periodic motions. When $B_i<$ 0.29, the system enters into the chaos, as shown in Fig. 14(a). Then, it turns into quasi-periodic motion as seen in Figs. 14(b)-(c), when $B_i$ reaches to 0.29 and 0.302, respectively. Later, the system goes into chaos again by the channel of quasi-periodic motion, as seen in Fig. 14(d). When $B_i$ keeps increasing to 0.363, the system bifurcates to period doubling motion which exists in a very narrow motion window. Subsequently, when $B_i=$ 0.377, the system changes to quasi-periodic motion again, as shown in Fig. 14(f). Finally, the system undergoes the chaos through the route of period-two state as seen in Figs. 14(h)-(i).

From Figs. 13(a)-(d), it clearly shows that as $\xi$ increases, the width of regions of chaos becomes narrow and the amplitude of displacement $Y$ decreases gradually. In other words, when $\xi$ increases from 0.03 to 0.09, the system becomes stable increasingly. Over the range of $B_i>$ 0.27, the system is always under the period motion including period-one and period-two motion at $\xi =$ 0.07. Furthermore, within the range of 0.636 $<B_i<$1, the vibration amplitude of the gear system keeps certain constant. Likewise, under $\xi =$ 0.09, the system is in the period motion state, which switches between period-one and period-two motions with the range of $B_i<$ 0.094 and always stays under the period-one state when 0.094 $<B_i<$ 1. In addition, the system occurs crisis phenomenon in Fig. 13(b, c), which are consistent with the conclusion obtained in Ref. [7].

Fig. 13Under lightly loaded condition, bifurcation diagrams of Bi with respect to Y when ξ is a) 0.03, b) 0.05, c) 0.07 and d) 0.09, respectively

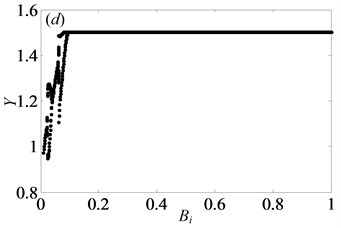
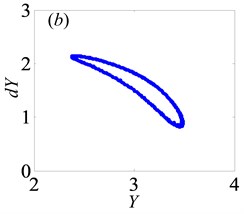
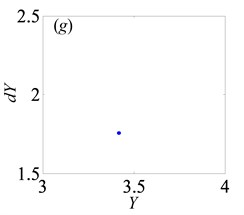
When $\mathrm{\Delta }=$ 2, the system is only in quasi-periodic motion state and the amplitude along the line of action keeps certain constant in the range of 0 $<B_i<$ 1, as shown in Fig. 15. For instance, when $B_i$ is chosen to 0.5, the phase portrait and Poincaré map are obtained in Fig. 16, which illustrate the system enters into quasi-periodic motion. It means that bearing clearance affects weakly on motion characteristics of gear system under heavily loaded condition.

Fig. 14Under lightly loaded condition, Poincaré maps of Y with respect to dY at ξ= 0.03, when Bi is a) 0.1, b) 0.29, c) 0.302, d) 0.34, e) 0.363, f) 0.377, g) 0.45, h) 0.55, and i) 0.634, respectively

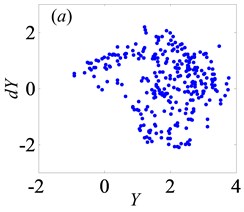
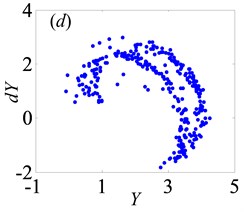
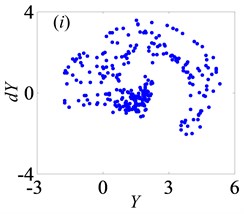
According to the analysis about the effect of dimensionless bearing clearance on bifurcation and chaos, it could be obtained that $B_i$ has considerable impact on bifurcation property under lightly loaded condition, which leads to different and complex types of motion states. Hence, it is essential to choose suitable bearing clearance for ensuring the stability of gear transmission and reducing the vibration intensity of the gear system.

Fig. 15Under heavily loaded condition, bifurcation diagrams of Bi versus Y

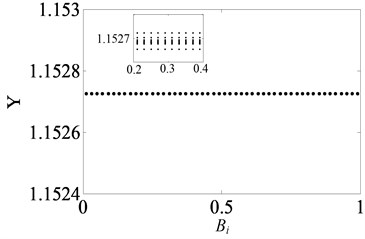
Fig. 16Under heavily loaded condition, phase portrait and Poincaré maps of Y with respect to dY when Bi= 0.5