Generalized gap function in the dynamic interaction problems of elements of vibrational technological machines with “not holding” ties

1. Introduction

Vibrating processes are widespread in production systems related to various branches of engineering. Vibrations are essential in the process of vibrational displacement, transportation facilities and working environments, they are widely used in machining technology (vibration cutting materials, vibration hardening etc.). The area displays vibration interactions related to the development direction of modern dynamics of machines. The theoretical basis of this direction is formed at the intersection of theoretical mechanics, theory of mechanisms and machines, oscillation theory, the theory of vibrational motion, the theory of vibration processes. Significant sections of the theory of vibration processes are in the area of nonlinear mechanics, nonlinear theory of oscillations and waves [1, 2].

In many cases vibration influence is considered as a factor of influence on a condition of the interacting parties of contact of the adjoining bodies. Features of “not holding” ties which are characteristic for technological processes of vibromovement, vibrohardening, vibration transportation, etc. are to a lesser extent studied.

In the offered article possibilities of development of the generalized approaches in the solution of problems of dynamic interactions of elements of technological systems with “not holding” ties are considered.

2. General provisions. Statement of research problems

Vibration interaction is used for development of new technological processes in which necessary quality of production is provided due to interaction of the loose environment with the vibrating surface. Examples of technical solutions which are based on the accounting of features of vibroshock processes for increase of physicomechanical properties of surfaces at impacts of small steel balls with details, are considered in work [4].

“Not holding” ties allow to realize processes of periodic impacts which are connected with opportunities of creation of vibrational technological processes.

Methods of mathematical modeling in problems of vibration interactions are known [7]. Such interactions are characteristic for technological processes of vibration movement, processes of vibration type which are used for processing of the contacting surfaces for the purpose of their hardening. Process of formation of interactions in systems with “not holding” ties can be considered as the process consisting of several phases. Such phases are contact phases at which reaction of ties is positive; a phase of a transition state when reaction is equal to zero; a gap phase in which the contacting surfaces can make the autonomous movements.

For validation of technological processes with continuous vibration tossing vibration technological machines, which appointment consists in formation of a certain structure of a vibration field, are used. Works, in which theoretical bases of creation and maintenance of one-dimensional fluctuations develop, gained the greatest fame.

The problem of realization of vibration technological processes has complex character. Technological machines are complex and contain aggregation and units in which between elements there are “not holding” contact. Approaches to permission of such problem demand the taking note of conditions of support of steady tossing processes of vibration and the taking note of formation of the modes of dynamic interactions which is dealing with reactions of ties and in contact interactions of compound structures of mechanisms and machines. Compound objects have some parts connected by the gravity or additional forces, and also elastic ties in which processes of violation of contacts or considerable fluctuations of sizes of contact forts can be shown.

Research problems are focused on formation of theoretical ideas of dynamic interactions of a solid body with the vibrating surface on the basis of development of mathematical models at introduction of additional external forces and elastic ties at the taking note of “not holding” contact, including, mathematical models of the gapless movement of compound solid bodies.

3. Mathematical modelling of processes of continuous tossing

The generalized approach to estimate of characteristics of movement forms of the particles with formation of a phase of free flight with the subsequent interaction with the vibrating surface develops. As the basic the mathematical model of interaction of a material particle with the horizontal surface fluctuating under the harmonious law is used. $H\left(t\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\omega }t\right)$. Features of interaction of a particle with a vibrating surface with the adjustment parameters of basic and advanced mathematical models are defined. Advanced models reflect the effect of additional forces and viscous friction.

Table 1 shows the main elements of analytic approach: the base model, due to parameters, a family of possible flight paths in phase (Fig. 1), the function of the gap, the conditions of separation. For comparison purposes opportunities of influence on process of adjusting parameters the concept of function of a gap is entered. Function of a gap allows to conduct the detailed research of properties of vibration interactions.

For the variant of the basic model, in which the surface is moving harmonically function of the gap takes the form:

The generalized approach on the basis of use of function of a gap assumes consideration of family of possible trajectories in a phase of free flight. The generalized approach on the basis of use of function of a gap assumes consideration of family of possible trajectories in a phase of free flight.

Fig. 1Set of possible trajectories: t0 = 0.01(n – 1) s, n = 1,…,20, A = 0,05 m, ω = 40 rad/s

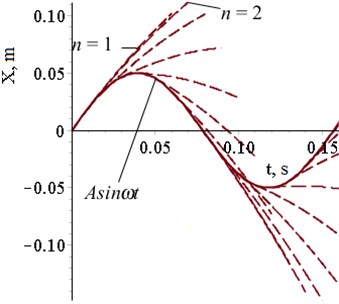
Within the framework of ideas about the function of the gap, the detachment conditions of a particle with unilateral constraints determined by the position of the particle or phase parameters of the harmonic process, certain relations between displacement, velocity, acceleration, sharpness (understood as the third derivative of the displacement by analogy with the concept of smoothness or sharpness of movement used in the problems of the dynamics of transport devices).

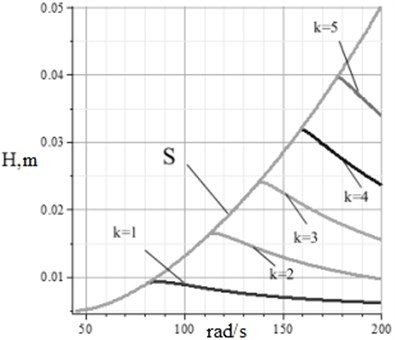
The regularities of formation of a trajectory with continuous tossing are investigated on the basis of the generalized approach. The mode with continuous tossing is understood as the mode with the period of free approach which duration is multiple to the period of vibration of the contacting surface. The role of frequency rate of the period of free flight in formation of properties of the modes with continuous tossing, etc. is established [8, 9]. In figure 2 the revealed dependences are presented.

Use of function of a gap and criteria of an assessment of possible forms and features of trajectories of the movement of material particles taking into account conditions of interactions with environment represents the generalized approach allowing a message search development in problems of dynamic synthesis of rational vibration technologies.

4. Definition of conditions of preservation of contact

General concepts about gapless interactions between components of mechanical oscillatory system with elastic connections, including with a support on the vibrating surface develop [10-14].

As components the solid bodies of the final sizes having a contact surface, perpendicular to the direction of the movement are considered.

Fig. 2The height of the flying up for the points of the second and third order in the implementation of the regime tossing a one-touch: the curve S – the height of the flying up of particle separation region of the third order, depending on the oscillation frequency at a fixed vibration amplitude A = 5 mm; curve k = 1., k = 5 graphs heights of flying up particles in the separation region of the second-order

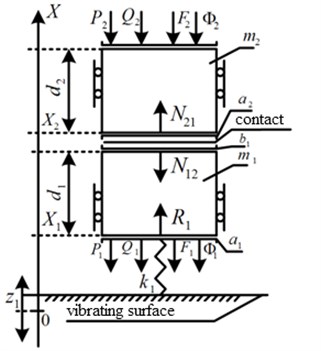
The mathematical model from two components (Fig. 3) with use of stiffness connections with the vibrating basic surface is considered. Thus between components violation of unilateral connection is possible.

The connection violation condition (emergence of a gap) is defined by parameters of the mass-inertia elements and stiffness ties. Analytical forms of the boundary ratios defining such movements at which vibration of the basis does not lead to connection violation are received. The concept about full, static and dynamic reaction of ties is entered.

Fig. 3A compound solid body on the elastic fluctuating basis Z1: Pi – powers of viscous friction; Qi – gravity; Fi – constant forces; N12, N21 – full contact reactions

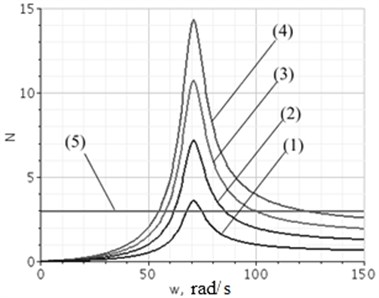
Amplitudes of oscillation of dynamic reaction (line 1-4) at various parameters of oscillation of a basic surface in comparison with static reaction are represented (line 5) in Fig. 4. Depending on parameters of mechanical system the equation of condition of preservation of the gapless movement reads:

where $p_i$ – coefficients of viscous friction, $k_i$ – stiffness coefficients, $f_c$ – constant force, $m_i$ – mass of elements, ${\omega }_1$, $A_1$ – are frequency and amplitude of oscillating surface.

Fig. 4Estimates of amplitude of fluctuation dynamic reaction components: 1, 2, 3, 4 – estimates dynamic components for amplitudes of kinematic indignation A1 from 1 to 4 mm; 5 – level of static reaction

In turn, the inequality Eq. (2) is interpreted as a set of points in amplitude-frequency area of gapless contact. In figure 5 the line of level G divides the plane of parameters $(A_1,{\mathrm{\omega }}_1)$ into two areas: I – area of the gapless movement, II – area of possible formation of a gap.

Fig. 5Amplitude-frequency area of contact: I – contact area; II – area of a possible gap; G – the line of level N21Σ for function A1⋅A(ω1); C – contact; D – possible gap

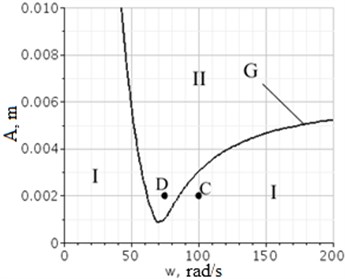
Sufficient conditions of gapless movement of components of mechanical oscillatory system are found in the steady state mode. It is shown that as factors of the gapless movement of system can be considered not only frequencies and amplitudes, but also ratios of mass of components, stiffness of connections, coefficients of viscous friction and external forces. The presented system of actions, rules of creation of mathematical models and analytical expressions can be considered as the developed method.

5. Conclusions

The generalized gap function which has allowed to formulate system of requirements and analytical relations for a possibility of realization of modes with continuous tossing is enter. It is shown that the generalized gap function can be used for definition of parameters of critical conditions in problems of dynamics of the compound solid realizing the forms of movement without gap of contacts between components. The technology of construction of families of trajectories is developed for processes continuous tossing taking into account frequency rate of the relation between time of free flight and the period of fluctuation of a surface. The algorithm of construction of the analytical relations determining limiting values of frequencies of external vibrating exciting which exceeding leads to gap of contacts is offered.