Abstract
Vibration exciters are of most important units of any vibratory equipment defining its design peculiarities, operational features, functional purpose, and performance characteristics. Among a great variety of vibration exciters, the unbalanced rotors are of the most widely used. The present research considers the possibilities of providing specific motion trajectories of the vibratory machines’ working members with the help of the planetary-type vibration exciter. The methodology of this study is divided into two main stages: deriving motion equations of an unbalanced mass located on a planet gear and analyzing the possibilities of generating rectilinear, elliptical, and circular motion paths by choosing the appropriate geometrical parameters of the planetary gear train. The results of the performed kinematic analysis are presented in the form of the unbalanced mass trajectories, velocities, and accelerations at different design parameters of the planetary-type mechanism. The main scientific novelty of the present study is substantiating the possibilities of using the single-degree-of-freedom planetary-type mechanism for generating the controllable motion trajectories of the unbalanced mass of an inertial vibration exciter. The obtained results can be practically implemented while developing novel adjustable drives for various vibratory equipment, particularly compactors, sieves, screens, and conveyors.
Highlights
- In an improved excitation mechanism, it is proposed to attach an unbalanced mass to the planet gear and to define the appropriate design parameters providing specific trajectories of the mass motion.
- The kinematic diagram of the mechanism is considered, and analytical expressions for calculating kinematic parameters (displacements, speeds, and accelerations) of the unbalanced mass are derived.
- The possibilities of generating circular, elliptical, and rectilinear motion of the unbalanced mass are substantiated. In addition, the speeds and accelerations of the unbalanced mass are analyzed.
1. Introduction
Compacting, sieving, screening, and conveying machines are of the most widespread vibratory equipment used in various industries, e.g., machine-building, mining, food-processing, pharmaceutical, agriculture, etc. In order to provide the best performance of the mentioned operations while processing different products, the used vibration exciter should be able to adjust its inertial characteristics according to the prescribed technological conditions [1]. In addition, the design peculiarities of the exciter influence the startup duration and energy consumption of the vibratory equipment [2], as well as the kinematic and dynamic characteristics of the working member (trajectory, velocity, acceleration, overloading, etc.) [3]. Considering the prospective fields of application of the controllable vibration exciters, they can be effectively implemented for such purposes as vibration-driven locomotion systems [4] and wheeled vibratory robots [5].
Numerous scientific papers are dedicated to the development and investigation of adjustable vibration exciters. The possibilities of equipping the vibratory machines with multi-motor drives actuating several unbalanced rotors that work synchronously are comprehensively studied in [6] and [7]. An enhanced design of the coaxial dual-rotor inertial vibration exciter is presented, theoretically investigated, and experimentally tested in [8]. The use of the controllable crank-type mechanism for driving various vibratory equipment is considered in [9], while the possibilities of its implementation for actuating the semidefinite oscillatory system are studied in [10].
From the scientific and practical viewpoint, the interesting and prospective designs of inertial vibration exciters can be developed on the basis of planetary-type mechanisms. For instance, the papers [11] and [12] consider the implementation of such exciters for actuating various construction and road-building machinery, snowplows, etc. The possibilities of developing multi-purpose adjustable planetary-type vibration exciters are thoroughly studied in [13, 14]. The paper [15] is focused on investigating the resonance effects that occur during the operation of a vibratory system actuated by the planetary-type exciter. In [16], the authors consider the torsional oscillations of a planetary gear train. The present investigations continue the authors’ previous research published in [17] and dedicated to generating triangular, rectangular, and similar multi-angular oscillations of a single-mass vibratory system driven by the planetary-type exciter. The main scientific novelty of the present study is substantiating the possibilities of using the single-degree-of-freedom planetary-type mechanism for generating the controllable motion trajectories (circular, elliptical, and rectilinear) of the unbalanced mass of an inertial vibration exciter.
2. Research methodology
2.1. General design of the laboratory prototype being studied
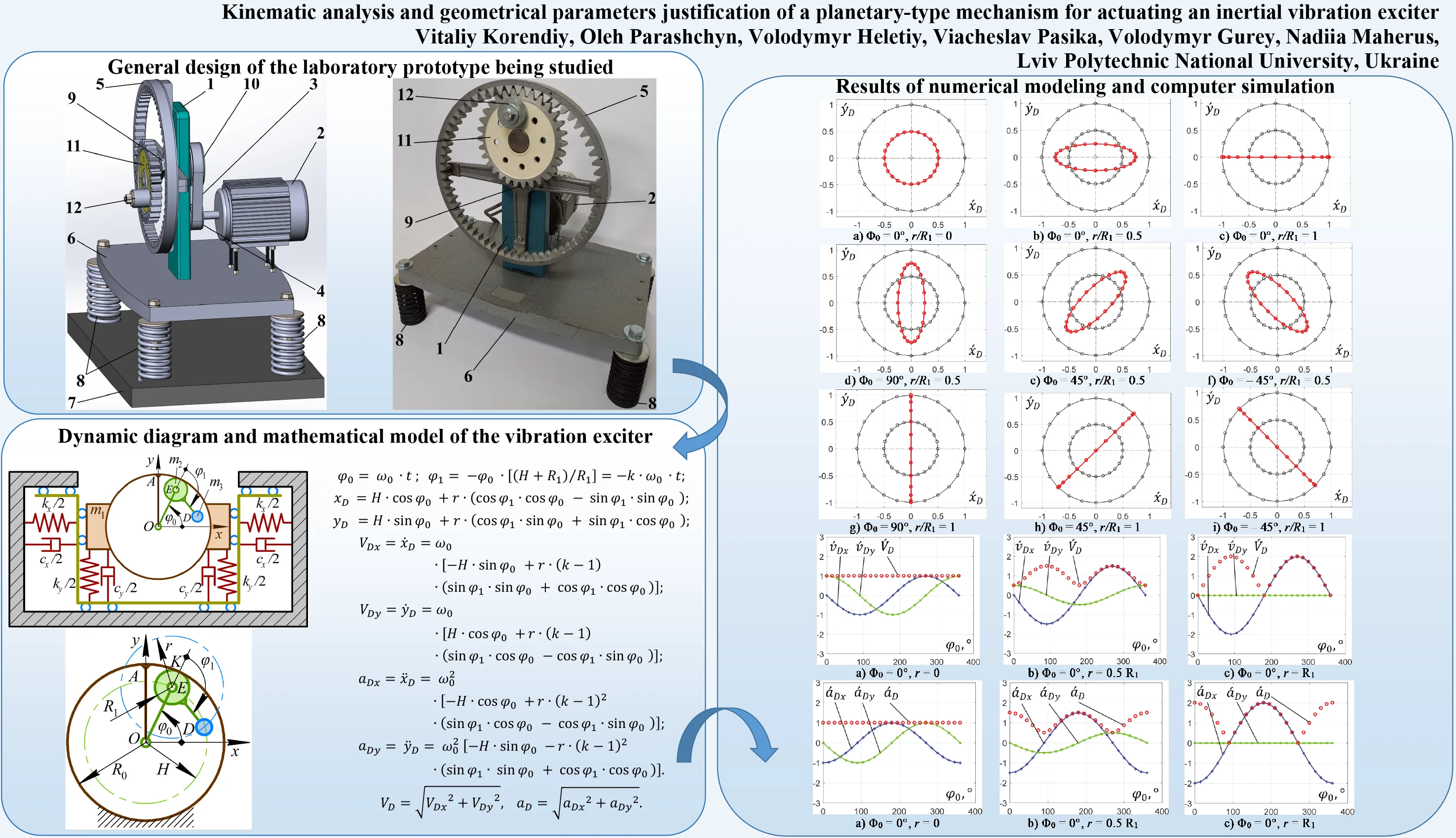
The laboratory prototype of the single-mass vibratory system (Fig. 1) consists of the planetary-type mechanism 1 driven by the electric motor 2 through the toothed belt transmission 3. The driving pulley 4 is fixed on the motor’s shaft. The ring gear 5 of the mechanism is mounted on the machine’s body 6 suspended from the stationary supporting surface 7 by the set of four coil-type cylindrical springs 8, which perform the vibration isolation function. The arm or, so-called, planet carrier 9 is fixed to the shaft of the driven pulley 10 of the toothed belt transmission 3. Another end of the carrier 9 is hinged to the axle, on which the planet gear 11 is installed. The unbalanced mass 12 is to be connected to the planet gear 11 at different points, and the dependence of the connection point location on the mass 12 trajectory is to be studied in the present paper. The major idea of this research is choosing the appropriate design (geometrical) parameters of the planetary gear train that allow for generating circular, elliptical, and rectilinear motion trajectories of the unbalanced mass. This, in turn, could provide the corresponding vibrations of the machine’s body.
Fig. 1General design of the laboratory prototype being studied

2.2. Kinematic diagram of the planetary-type mechanism of the vibration exciter
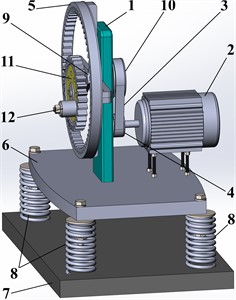
The dynamic diagram of the single-mass vibratory system equipped with the planetary-type vibration exciter is presented in Fig. 2(a). The rigid body of the mass can perform planar oscillations along the horizontal () and vertical () axes and is suspended from the stationary base by a set of spring-damper elements. The latter are characterized by the stiffness coefficients , and viscous friction factors , . The system motion is generated due to the action of the inertial forces exerted on the planet gear (mass ) and unbalanced mass during their uniform rotation around two mutually perpendicular axes located at hinges and .
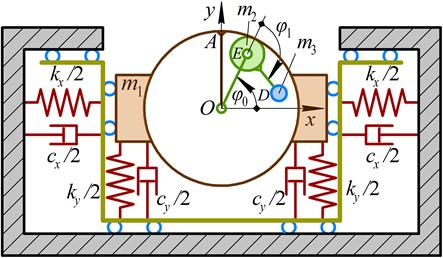
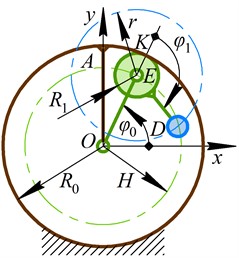
Taking into account the main idea of this research mentioned in the previous section, let us consider the corresponding kinematic diagram of the planetary-type mechanism used for actuating the proposed inertial vibration exciter (see Fig. 1(b)). The ring gear of the planetary-type mechanism is supposed to be fixed, while the rotation of the arm (planet carrier) is characterized by the angular coordinate . Considering the geometrical parameters of the planetary-type mechanism (, , , ) and assuming the constant angular speed of the arm , let us define the basic relations between the angles and :
where .
Fig. 2a) Dynamic diagram of the oscillatory system and b) kinematic diagram of the planetary-type mechanism of the vibration exciter
a)
b)
2.3. Analytical dependencies for determining the kinematic parameters of the mechanism
Considering the coordinate system with its origin at point , let us derive the analytical expression for determining the horizontal and vertical position of the unbalanced mass :
Based on Eqs. (2) and (3), the corresponding formulas for calculating the horizontal and vertical velocities and accelerations of the unbalanced mass can be deduced:
The full speed and acceleration of the unbalanced mass are following:
While performing kinematic analysis, it is more informative to consider the dimensionless analogues of the displacements, speeds, and accelerations instead of their absolute values:
3. Results and discussion
3.1. Simulating the trajectories of the unbalanced mass motion
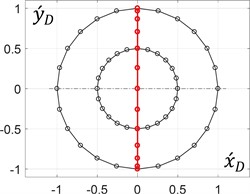
During the rotation of an arm (planet carrier) at a constant angular speed, it is enough to consider its single revolution to plot the corresponding trajectories of the unbalanced mass in the dimensionless values (see Eq. (9)). The results (Fig. 3) were obtained for the following constant relations between the mechanism geometrical parameters: 0.5 and 0.5, whilst the ratio and the initial angle of the arm (0, 0) are considered changeable.
Fig. 3Dimensionless trajectories of the unbalanced mass motion
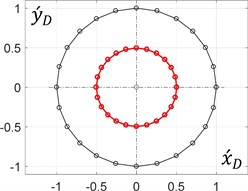
a) 0°, 0
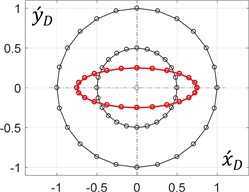
b) 0°, 0.5
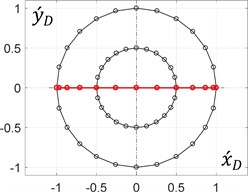
c) 0°, 1
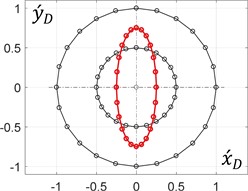
d) 90°, 0.5
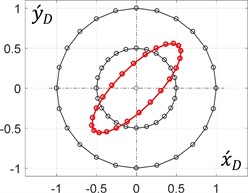
e) 45°, 0.5
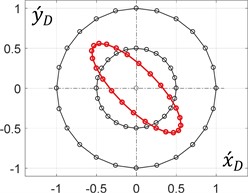
f) – 45°, 0.5
g) 90°, 1
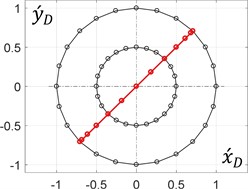
h) 45°, 1
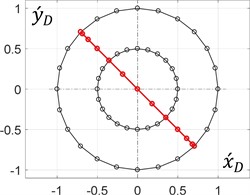
i) – 45°, 1
The obtained results allow for the conclusion that the circular trajectory of the unbalanced mass can be obtained when the distance between the mass and the planet gear axis is equal to zero ( = 0). All the other ratios within the range of (0…1) provide elliptical paths, whose major axes make the angles with the axis. Similarly, the ratio = 1 allows for generating rectilinear motion of the unbalanced mass at different angles with the horizontal axis.
Considering the possible practical implementation of the obtained results, the following conclusions can be drawn. Vertical rectilinear and elliptical trajectories of the unbalanced mass and, as a consequence, of the working member can be used in vibratory compacting machines. Horizontal rectilinear and circular paths can be implemented in screening and sieving equipment. In addition, a circular trajectory of a working member should be provided in vibratory lapping and polishing machines. Inclined rectilinear and elliptical trajectories are preferable for conveying equipment. Various rectilinear paths can be used in vibration-driven locomotion systems.
3.2. Analyzing the speeds and accelerations of the unbalanced mass
In order to perform further analysis, let us consider three basic cases of the unbalanced mass motion (see Figs. 3(a)-(c)): 0.5, 0.5, 0°, at the following changeable ratios 0, 0.5, 1. The plots describing the dependencies of the analogues of speeds and accelerations of the unbalanced mass at different ratios are presented in Figs. 4 and 5. Under the conditions of 0, the full speed of the unbalanced mass is equal to the speed of the planet gear hinge, while the corresponding horizontal and vertical components periodically reach the maximal values with the phase shift of 90°. Similarly, the full acceleration is equal to the centrifugal acceleration of the unbalanced mass rotating around the crankshaft. The elliptical motion characterized by the horizontal position of the ellipse major axis is also accompanied by the periodical change in the horizontal and vertical speeds and accelerations. In this case, the horizontal quantities take larger peak values than the vertical ones. Considering the rectilinear motion, the vertical components of the speeds and accelerations are equal to zero, while the full speed and acceleration are equal to the horizontal ones and periodically change reaching the maximal values that are twice larger than the ones obtained under the conditions of circular motion. This substantiates the possibilities of implementing the considered planetary-type mechanism with an unbalanced mass for actuating the inertial vibration exciter, which, in turn, can be used for actuating various vibratory equipment, e.g., screens, conveyors, compactors, etc.
Fig. 4Dependencies of analogues of the unbalanced mass speeds on the rotation angle
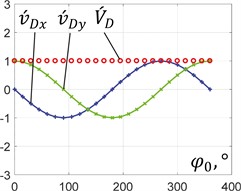
a) 0°, 0
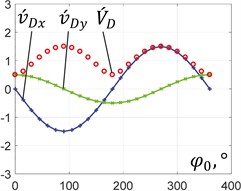
b) 0°,
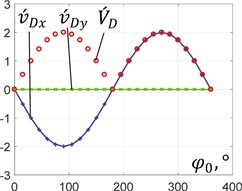
c) 0°,
Fig. 5Dependencies of analogues of the unbalanced mass accelerations on the rotation angle
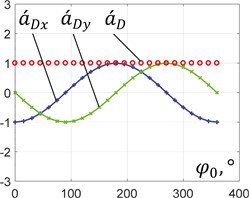
a) 0°, 0
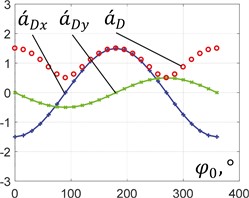
b) 0°,
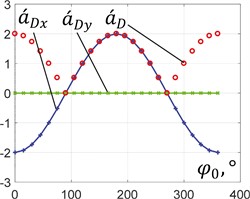
c) 0°,
4. Conclusions
The paper considers the possibilities of implementing the planetary-type mechanism for actuating the inertial vibration exciter with the aim of generating circular, elliptical, and rectilinear oscillations of the single-mass vibratory system. It is proposed to attach an unbalanced mass to the planet gear and to define the appropriate design (geometrical) parameters of the mechanism providing the mentioned trajectories of the unbalanced mass motion. The corresponding kinematic diagram of the mechanism is considered, and the analytical expressions for calculating the basic kinematic parameters (horizontal and vertical displacements, speeds, and accelerations) of the unbalanced mass are derived. The trajectories of the unbalanced mass are plotted at different geometrical parameters of the planetary-type mechanism. The possibilities of generating circular, elliptical, and rectilinear motion of the unbalanced mass are substantiated. In addition, the speeds and accelerations of the unbalanced mass are analyzed for the case when the arm (planet carrier) is initially located in the horizontal position. The obtained results can be used while developing novel adjustable drives for various vibratory equipment. Particularly, vertical rectilinear and elliptical trajectories can be used in vibratory compactors; horizontal rectilinear and circular paths can be implemented in sieves and screens; inclined rectilinear and elliptical trajectories can be used in vibratory conveyors. Further investigations on the subject of the paper may be focused on studying the dynamic behavior of various vibratory systems equipped with the considered exciter.
References
-
S. Kilikevičius, K. Liutkauskienė, R. Česnavičius, A. Keršys, and R. Makaras, “Investigation of the motion characteristics of parts on a platform subjected to planar oscillations,” Applied Sciences, Vol. 13, No. 17, p. 9576, Aug. 2023, https://doi.org/10.3390/app13179576
-
J. Feliks and P. Tomach, “The impact of vibrating screen startup time on vibration amplitude and energy consumption in transient state,” Energies, Vol. 16, No. 20, p. 7129, Oct. 2023, https://doi.org/10.3390/en16207129
-
O. Kachur and V. Korendiy, “Dynamic behavior of vibratory screening conveyor equipped with crank-type exciter,” in Lecture Notes in Mechanical Engineering, pp. 44–53, 2023, https://doi.org/10.1007/978-3-031-32774-2_5
-
V. Korendiy, V. Gursky, O. Kachur, P. Dmyterko, O. Kotsiumbas, and O. Havrylchenko, “Mathematical model and motion analysis of a wheeled vibro-impact locomotion system,” Vibroengineering Procedia, Vol. 41, pp. 77–83, Apr. 2022, https://doi.org/10.21595/vp.2022.22422
-
V. Korendiy and O. Kachur, “Locomotion characteristics of a wheeled vibration-driven robot with an enhanced pantograph-type suspension,” Frontiers in Robotics and AI, Vol. 10, p. 1239137, Aug. 2023, https://doi.org/10.3389/frobt.2023.1239137
-
M. Zou, P. Fang, Y. Hou, and H. Peng, “Investigation on multiple-frequency synchronization experiment of vibration system with dual-rotor actuation,” Mechanical Systems and Signal Processing, Vol. 164, p. 108261, Feb. 2022, https://doi.org/10.1016/j.ymssp.2021.108261
-
Y. Jia, N. Zhang, and Z. An, “Self-synchronization theory of circular symmetrical four motors,” Journal of Physics: Conference Series, Vol. 2174, No. 1, p. 012078, Jan. 2022, https://doi.org/10.1088/1742-6596/2174/1/012078
-
V. Gurskyi, V. Korendiy, P. Krot, R. Zimroz, O. Kachur, and N. Maherus, “On the dynamics of an enhanced coaxial inertial exciter for vibratory machines,” Machines, Vol. 11, No. 1, p. 97, Jan. 2023, https://doi.org/10.3390/machines11010097
-
O. Lanets, O. Kachur, V. Korendiy, and V. Lozynskyy, “Controllable crank mechanism for exciting oscillations of vibratory equipment,” in Lecture Notes in Mechanical Engineering, Cham: Springer International Publishing, 2021, pp. 43–52, https://doi.org/10.1007/978-3-030-77823-1_5
-
V. Korendiy, V. Gursky, O. Kachur, V. Gurey, O. Havrylchenko, and O. Kotsiumbas, “Mathematical modeling of forced oscillations of semidefinite vibro-impact system sliding along rough horizontal surface,” Vibroengineering PROCEDIA, Vol. 39, pp. 164–169, Dec. 2021, https://doi.org/10.21595/vp.2021.22298
-
A. Kim, M. Doudkin, A. Ermilov, G. Kustarev, M. Sakimov, and M. Mlynczak, “Analysis of vibroexciters working process of the improved efficiency for ice breaking, construction and road machines,” Journal of Vibroengineering, Vol. 22, No. 3, pp. 465–485, May 2020, https://doi.org/10.21595/jve.2020.20446
-
M. Marek, G. Kustarev, and N. Andrjuchov, “Theoretical studies and conditions analysis of the inertial slider slippage of asymmetric planetary vibration exciter for snowplow,” Bulletin of D. Serikbayev EKTU, No. 3, pp. 63–78, 2021, https://doi.org/10.51885/1561-4212_2021_3_63
-
V. V. Mikheyev and S. V. Saveliev, “Planetary adjustable vibratory exciter with chain gear,” in Journal of Physics: Conference Series, Vol. 1210, No. 1, p. 012097, Mar. 2019, https://doi.org/10.1088/1742-6596/1210/1/012097
-
V. V. Mikheyev, “New type of vibration generator with vibratory force oriented in preferred direction,” Journal of Vibration Engineering and Technologies, Vol. 6, No. 2, pp. 149–154, Apr. 2018, https://doi.org/10.1007/s42417-018-0025-4
-
R. Palevicius and K. Ragulskis, “The self-resonance effect of the planetary vibration excitation systems,” Journal of Vibroengineering, Vol. 14, No. 1, pp. 244–249, Mar. 2012.
-
G. Huo et al., “Torsional vibration modelling of a two-stage closed differential planetary gear train,” in Proceedings of the 11th IFToMM International Conference on Rotordynamics, Vol. 140, pp. 188–201, 2024, https://doi.org/10.1007/978-3-031-40459-7_13
-
V. Korendiy, V. Gurey, V. Borovets, O. Kotsiumbas, and V. Lozynskyy, “Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter,” Vibroengineering Procedia, Vol. 43, pp. 7–13, Jun. 2022, https://doi.org/10.21595/vp.2022.22703
Cited by
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
