Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

Kachur, Oleksandr; Korendiy, Vitaliy; Lanets, Oleksii; Kachmar, Roman; Nazar, Ihor; Heletiy, Volodymyr

doi:10.21595/vp.2023.23175

Vibroengineering Procedia

Browse Procedia

Published: 11 February 2023

Check for updates

Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

Oleksandr Kachur¹

Vitaliy Korendiy²

Oleksii Lanets³

Roman Kachmar⁴

Ihor Nazar⁵

Volodymyr Heletiy⁶

^{1, 3}Department of Robotics and Integrated Mechanical Engineering Technologies, Lviv Polytechnic National University, Lviv, Ukraine

^{2, 6}Department of Technical Mechanics and Dynamics of Machines, Lviv Polytechnic National University, Lviv, Ukraine

⁴Department of Motor Vehicle Transport, Lviv Polytechnic National University, Lviv, Ukraine

⁵Department of Oil and Gas Engineering and Welding, Lviv Polytechnic National University, Lviv, Ukraine

Corresponding Author:

Vitaliy Korendiy

Cite the article Download PDF

Abstract

Vibratory screening, sieving, and conveying processes are widely used in various industries. Among a great variety of vibration exciters, the unbalanced rotors are the most reliable, simple, and widespread ones. Due to the changeable operating conditions of vibratory equipment, in some cases, there occurs a necessity to control the disturbance (excitation) parameters of the corresponding drives. The primary purpose of this study is to substantiate the design parameters and analyze the dynamic characteristics of the vibratory screening conveyor based on the single-mass oscillatory system, and equipped with the controllable centrifugal exciter. The research methodology consists of several basic stages: developing the conveyor’s dynamic diagram and deducing the differential equations of the system’s motion; designing the machine’s 3D-model and defining its main geometrical and inertial parameters; numerical modeling of the system’s oscillations in the Mathematica software; simulating the conveyor’s operation in the SolidWorks software. The research results present the time dependencies of the conveyor’s working member kinematic parameters at different eccentricities of the unbalanced mass. The main scientific novelty of this research is substantiating the idea and possibilities of implementing the enhanced controllable centrifugal exciter for changing the disturbance (excitation) conditions of the vibratory screening and conveying machines. The proposed ideas and obtained results can be used by researchers and designers of similar equipment while developing control systems for regulating its operational efficiency (performance) in accordance with the changeable loading conditions or technological requirements.

Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

Highlights

The improved design of the vibratory screening conveyor based on the single-mass oscillatory system and equipped with the controllable centrifugal exciter (adjustable unbalanced rotor) is developed.
The mathematical model of the conveyor’s oscillatory system is deduced, and the numerical modeling of its operational conditions is carried out at different eccentricities of the unbalanced mass.
The computer simulation (virtual experiment) of the conveyor operation is performed in SolidWorks Motion software, and the basic dynamic parameters of the working member oscillations are analyzed.

1. Introduction

In various industries, particularly food, pharmaceutical, chemical, machine-building, mining, agricultural ones, etc., the main technological processes are accompanied with the screening, sieving, and conveying operations. In a wide range of cases, these operations are performed with the help of vibratory equipment. Among a great variety of vibration exciters, the unbalanced rotors are the most reliable, simple, and widespread ones. The vibratory equipment can be equipped with single-mass, double-mass, three-mass, and multi-mass oscillatory systems. A thorough comparative analysis of two vibratory screens with single-mass and double-mass oscillatory systems is presented in [1]. The problems of studying the loading characteristics and verifying the reliability parameters of vibratory screening and conveying machines are comprehensively studied in numerous scientific publications, particularly in [2, 3]. Another field of investigations, e.g. [4, 5], is dedicated to the optimization of the vibratory equipment design and operational parameters with the purpose of providing improved performance or meeting the increased technological requirements. The influence of different factors on vibratory screening accuracy is comprehensively studied in [6]. The thorough design calculations and performance analysis of certain elements of the screens are presented in [7, 8]. The problems of investigating the dynamic behavior of various types of vibratory screens are also widely covered in numerous papers, particularly in [9, 10]. The paper [11] is focused on the practical implementation of the vibratory sieving theory while improving the tea sieving machine.

The present paper is entirely based on the previous investigations of the authors. The initial design of the controllable crank-type vibration exciter was proposed in [12]. The enhanced inertial exciter equipped with two coaxially installed unbalanced rotors actuated by independent drives is presented in [13]. The papers [14, 15] are dedicated to the dynamic analysis of different vibratory systems driven by the novel planetary-type inertial exciters. The author’s last paper [16] is focused on analyzing the dynamic characteristics of the improved coaxial inertial exciter with a single electric motor under different operational conditions. The primary purpose of the present research is to substantiate the design parameters and study the dynamic behavior of the single-mass vibratory screening conveyor equipped with the controllable centrifugal exciter.

2. Research methodology

2.1. 3D-model of the vibratory screening conveyor and the enhanced centrifugal exciter

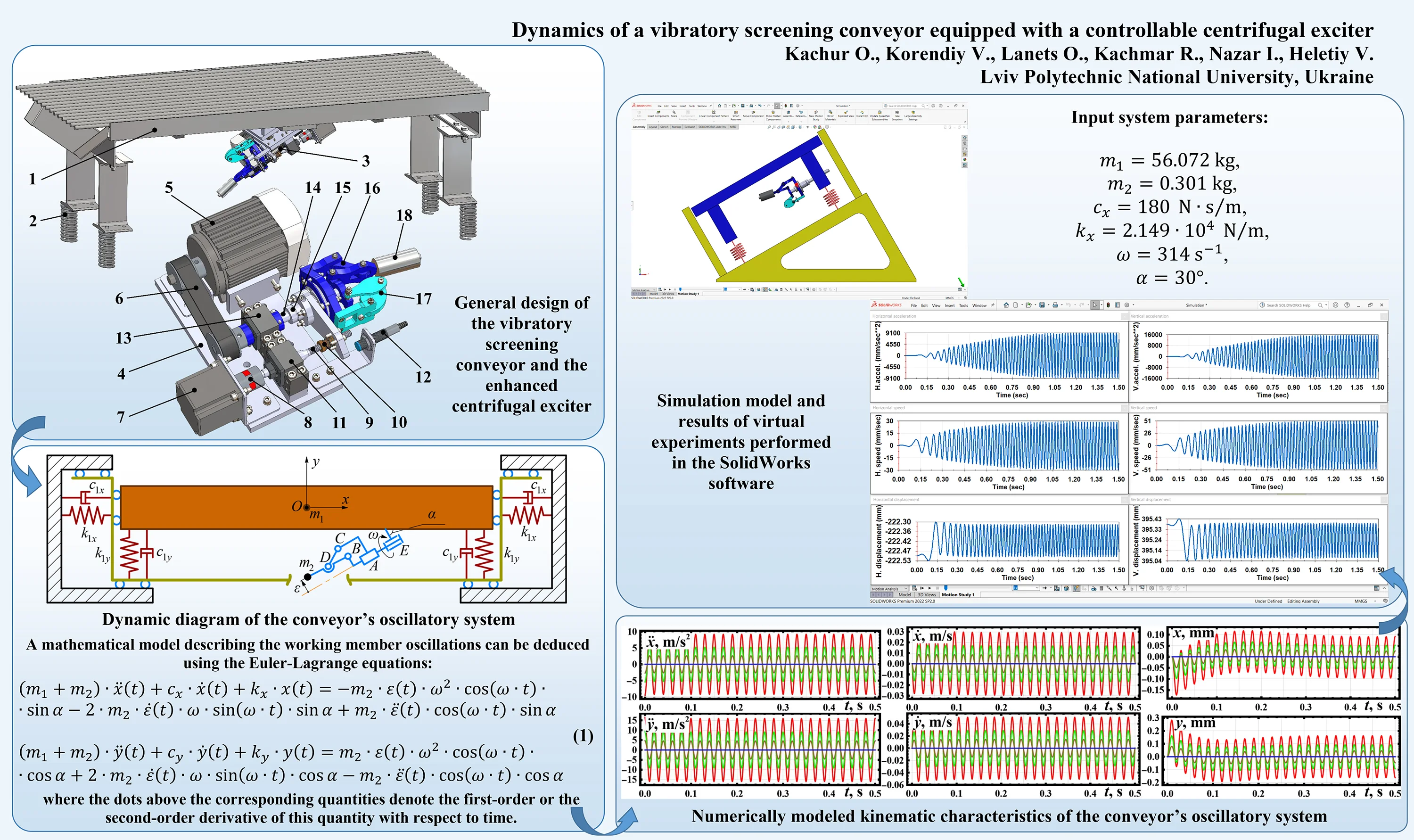
The considered vibratory screening conveyor (Fig. 1) consists of the working member 1, vibration isolators (cylindrical coil springs) 2, and electromechanical exciter 3. The working member 1 contains the lower conveying tray (chute) and the upper rod-type screen.

Fig. 1General design of the vibratory screening conveyor and the enhanced centrifugal exciter

The enhanced vibration exciter (Fig. 1) consists of the base 4, on which all the elements are installed. The servo motor 5 sets the belt transmission 6 into motion. The driven pulley is fixed on the main shaft 14 installed in the bearing support 13. The use of the linear (guide, pilot) ball bearing 15 allows for changing the angular position of the rocker 16 and the eccentricity of the unbalanced mass 18. The passive balancing mechanism 17 is applied to ensure the zero-value inertial parameters of the exciter in its folded position, providing zero centrifugal force. The active eccentricity control system consists of the step motor 7, jaw clutch 8, and lead (screw) shaft 9 installed in the bearing support 11. The spring-loaded nut 10 is fixed on the sliding plate installed on the guide (pilot) bearing 15. In order to define the end position of the sliding plate, the inductive sensor 12 is used. The operation of the considered centrifugal exciter can be described as follows. The servo motor’s shaft sets the unbalanced mass into the rotary motion through the belt transmission. The unbalanced mass eccentricity controlled by the step motor defines the magnitude of the centrifugal force, which periodically changes its direction and disturbs (excites) the oscillations of the conveyor’s working member.

2.2. Dynamic diagram and mathematical model of the conveyor’s oscillatory system

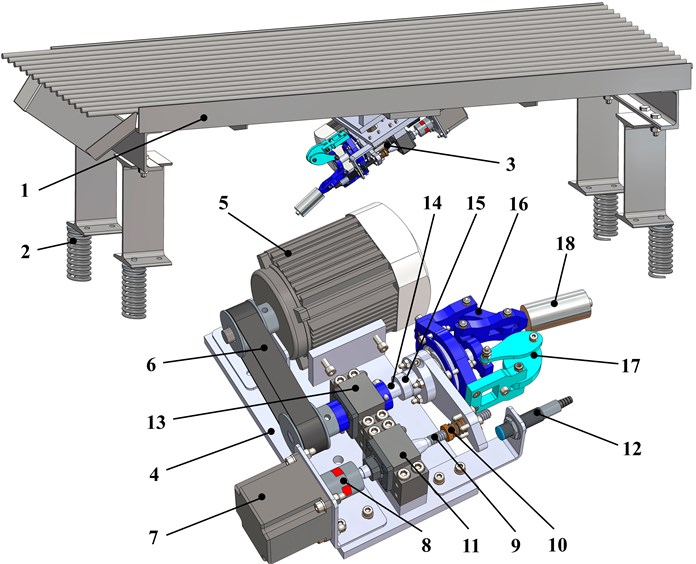
The simplified dynamic diagram of the conveyor’s oscillatory system is shown in Fig. 2. The working member is modeled as a rigid body of the mass $m_{1}$ . The body is suspended from the stationary base by the system of spring-damper elements, characterized by the stiffness coefficients $k_{1 x} = 0.5 k_{x}$ , $k_{1 y} = 0.5 k_{y}$ and viscous friction (damping) coefficients $c_{1 x} = 0.5 c_{x}$ , $c_{1 y} = 0.5 c_{y}$ . The oscillations are excited by the unbalanced rotor hinged to the body at the point $E$ . The angular speed (forced cyclic frequency) is assumed constant and equal to $ω$ . In the simplified diagram, the control system regulating the position (eccentricity $ε$ ) of the unbalanced mass $m_{2}$ is omitted. Let us consider the case when the eccentricity $ε$ and forced cyclic frequency $ω$ are the controllable parameters allowing for adjusting the system operational parameters (amplitudes, velocities, accelerations) in accordance with the technological requirements.

A mathematical model describing the working member oscillations can be deduced using the Euler-Lagrange equations:

1

(m_{1} + m_{2}) ∙ \ddot{x} (t) + c_{x} ∙ \dot{x} (t) + k_{x} ∙ x (t) = - m_{2} ∙ ε (t) ∙ ω^{2} ∙ \cos (ω ∙ t) ∙ \sin α - 2 ∙ m_{2} ∙ \dot{ε} (t) ∙ ω ∙ \sin (ω ∙ t) ∙ \sin α

+ m_{2} ∙ \ddot{ε} (t) ∙ \cos (ω ∙ t) ∙ \sin α,

(m_{1} + m_{2}) ∙ \ddot{y} (t) + c_{y} ∙ \dot{y} (t) + k_{y} ∙ y (t) = m_{2} ∙ ε (t) ∙ ω^{2} ∙ \cos (ω ∙ t) ∙ \cos α

+ 2 ∙ m_{2} ∙ \dot{ε} (t) ∙ ω ∙ \sin (ω ∙ t) ∙ \cos α - m_{2} ∙ \ddot{ε} (t) ∙ \cos (ω ∙ t) ∙ \cos α,

where the dots above the corresponding quantities denote the first-order or the second-order derivative of this quantity with respect to time.

Fig. 2Dynamic diagram of the conveyor’s oscillatory system

3. Results and discussion

3.1. Numerical modeling of the system oscillations in the Mathematica software

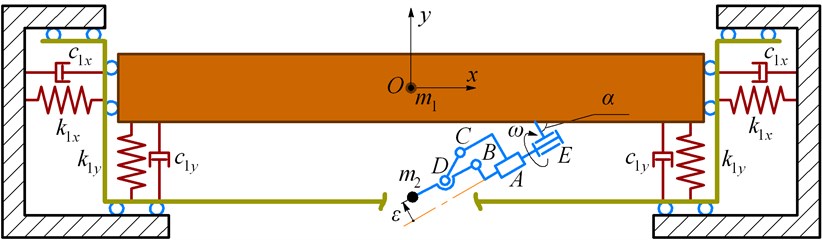
Let us study the conveyor’s oscillations by numerical solving of the system of differential equations (1) in the Mathematica software with the help of the Runge-Kutta methods. The following input parameters are considered: $m_{1} =$ 56.072 kg, $m_{2} =$ 0.301 kg, $c_{x} =$ 180 (N∙s)/m, $k_{x} =$ 2.149∙10⁴ N/m, $ω =$ 314 s^-1, $α =$ 30°. The numerical modeling is carried out for the following values of the unbalanced mass eccentricity $ε$ : 0, 10, 20, 35 mm. The results are shown in Fig. 3 by the blue, brown, green, and red lines, respectively. Horizontal and vertical amplitudes vary from zero at $ε =$ 0 mm to 0.1 mm and 0.16 mm, respectively, at $ε =$ 35 mm. The maximal values of the corresponding speeds reach 0.03 m/s and 0.05 m/s. Horizontal acceleration is about 9 m/s², while the vertical one exceeds the value of 16 m/s². This allows for concluding about the detachable motion conditions when the parts being conveyed are jumping (bouncing) over the conveying (screening) surface. In addition, the obtained results substantiate the initial idea of this research: by controlling the eccentricity of the unbalanced mass, it is possible to adjust the machine’s operational conditions in accordance with the technological requirements set for different materials to be conveyed and sieved. Considering the case of $ε =$ 10 mm, the amplitude values of the horizontal and vertical displacements are about 0.03 mm and 0.05 mm, speeds – 0.009 m/s and 0.015 m/s, accelerations – 2.5 m/s² and 4.5 m/s². At $ε =$ 20 mm, the corresponding values of the system’s kinematic parameters are the following: 0.06 mm and 0.09 mm, 0.018 m/s and 0.03 m/s, 5 m/s² and 9 m/s².

Fig. 3Numerically modeled kinematic characteristics of the conveyor’s oscillatory system

3.2. Simulation of the conveyor operation in the SolidWorks software

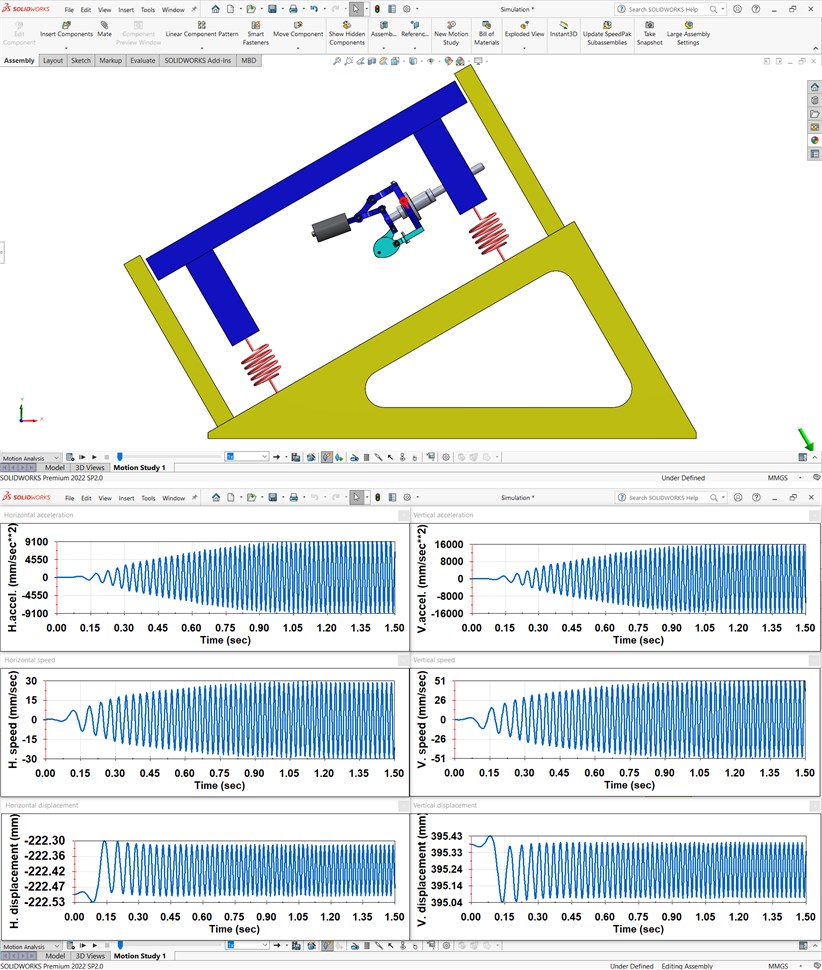
Let us verify the correctness of the obtained numerical modeling results by computer simulation (virtual experiment) of the conveyor operation with the help of the SolidWorks Motion software. In the considered case, let us adopt the eccentricity of $ε =$ 35 mm. The corresponding simulation model and results are presented in Fig. 4. All the parameters of the considered oscillatory system are similar to those mentioned above. Unlike the numerical modeling, the simulation in the Solidworks Motion software allows for taking into account the simplified operational parameters of the electric drive used for actuating the oscillatory system. The transient (starting) conditions last for about 0.8 s. Analyzing the obtained simulation results, the conclusions about their satisfactory agreement with the numerical modeling results can be drawn. The amplitude values of the horizontal and vertical displacements are about 0.1 mm and 0.16 mm, speeds – 30 mm/s and 51 mm/s, accelerations – 9100 mm/s² and 16000 mm/s².

The experimental prototype of the considered vibratory screening conveyor (Fig. 1) has been manufactured at the Vibroengineering Laboratory of Lviv Polytechnic National University and is currently being tested under different operational conditions. Further research on this subject is focused on developing the automatic control system adjusting the conveyors’ excitation parameters (forced frequency and unbalanced mass eccentricity) in accordance with the operational conditions (effective (useful) load, conveying speed, overloading factor, etc.) and technological requirements set for different types of materials to be conveyed and sieved.

Fig. 4Simulation model and results of virtual experiments performed in the SolidWorks software

4. Conclusions

The presented paper is focused on studying the dynamic behavior of the vibratory screening conveyor under different operational conditions. The enhanced centrifugal exciter is proposed and implemented in the conveyor’s single-mass oscillatory system. The corresponding dynamic diagram is constructed, and the differential equations describing the system motion are deduced. Using the Mathematica software, the numerical modeling of the system oscillations is carried out. The verification of the theoretically obtained results is performed in the Solidworks software using the conveyor’s simulation model. The results show that the horizontal and vertical amplitudes of the working member vary from zero at $ε = 0 m m$ to 0.1 mm and 0.16 mm, respectively, at $ε =$ 35 mm. The maximal values of the corresponding speeds reach 0.03 m/s and 0.05 m/s. Horizontal acceleration is about 9 m/s², while the vertical one exceeds the value of 16 m/s², ensuring the detachable motion conditions when the parts being conveyed are jumping (bouncing) over the conveying (screening) surface. The performed studies can be used while developing control systems for regulating the conveyor operational efficiency in accordance with the changeable loading conditions or technological requirements.

References

C. Yu et al., “Comparison of flip-flow screen and circular vibrating screen vibratory sieving processes for sticky fine particles,” Minerals Engineering, Vol. 187, p. 107791, Sep. 2022, https://doi.org/10.1016/j.mineng.2022.107791

Publisher
P. Krot et al., “Development and verification of the diagnostic model of the sieving screen,” Shock and Vibration, Vol. 2020, pp. 1–14, Jun. 2020, https://doi.org/10.1155/2020/8015465

Publisher
H. Khoshdast, H. Khoshdast, and S. Jalilifard, “Dynamic analysis of a dashpots equipped vibrating screen using finite element method,” Physicochemical Problems of Mineral Processing, Vol. 57, No. 1, pp. 112–126, Nov. 2020, https://doi.org/10.37190/ppmp/130001

Publisher
F. Safranyik, B. M. Csizmadia, A. Hegedus, and I. Keppler, “Optimal oscillation parameters of vibrating screens,” Journal of Mechanical Science and Technology, Vol. 33, No. 5, pp. 2011–2017, May 2019, https://doi.org/10.1007/s12206-019-0403-1

Publisher
V. Borovets, O. Lanets, V. Korendiy, and P. Dmyterko, “Volumetric vibration treatment of machine parts fixed in rotary devices,” in Lecture Notes in Mechanical Engineering, pp. 373–383, 2021, https://doi.org/10.1007/978-3-030-68014-5_37

Publisher
H. Yan, Y. Li, F. Yuan, F. Peng, X. Yang, and X. Hou, “Analysis of the screening accuracy of a linear vibrating screen with a multi-layer screen mesh,” Strojniški vestnik – Journal of Mechanical Engineering, Vol. 66, No. 5, pp. 289–299, May 2020, https://doi.org/10.5545/sv-jme.2019.6523

Publisher
Y. Wei, C. Tao, L. Zheng, and M. Huang, “Design of vibrating screen separation equipment for powder materials,” in Journal of Physics: Conference Series, Vol. 2235, No. 1, p. 012028, May 2022, https://doi.org/10.1088/1742-6596/2235/1/012028

Publisher
L. Peng, H. Feng, Z. Wang, H. Wang, H. Yang, and H. Huang, “Screening mechanism and properties of a cantilevered vibrating sieve for particles processing,” Applied Sciences, Vol. 9, No. 22, p. 4911, Nov. 2019, https://doi.org/10.3390/app9224911

Publisher
X. Nguyen, K. L. Nguyen, and G. N. Dinh, “Study of the dynamics and analysis of the effect of the position of the vibration motor to the oscillation of vibrating screen,” Journal of Physics: Conference Series, Vol. 1384, No. 1, p. 012035, Nov. 2019, https://doi.org/10.1088/1742-6596/1384/1/012035

Publisher
T. Bento Linhares and C. Bruno Santos Vimieiro, “Analysis of the dynamic forces acting on a vibrating screen and its support structure using a scale model,” Measurement, Vol. 176, p. 109179, May 2021, https://doi.org/10.1016/j.measurement.2021.109179

Publisher
Z. Zhao, H. Zhu, G. Chen, J. Zhong, and L. Chen, “Analysis of influence factors on the sieving efficiency in tea vibration sieving,” Agricultural Research, Vol. 8, No. 2, pp. 279–286, Jun. 2019, https://doi.org/10.1007/s40003-018-0381-z

Publisher
O. Lanets, O. Kachur, V. Korendiy, and V. Lozynskyy, “Controllable crank mechanism for exciting oscillations of vibratory equipment,” in Lecture Notes in Mechanical Engineering, pp. 43–52, 2021, https://doi.org/10.1007/978-3-030-77823-1_5

Publisher
V. Gursky, P. Krot, V. Korendiy, and R. Zimroz, “Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines,” Machines, Vol. 10, No. 2, p. 130, Feb. 2022, https://doi.org/10.3390/machines10020130

Publisher
V. Korendiy, I. Kuzio, S. Nikipchuk, O. Kotsiumbas, and P. Dmyterko, “On the dynamic behavior of an asymmetric self-regulated planetary-type vibration exciter,” Vibroengineering Procedia, Vol. 42, pp. 7–13, May 2022, https://doi.org/10.21595/vp.2022.22580

Publisher
V. Korendiy, V. Gurey, V. Borovets, O. Kotsiumbas, and V. Lozynskyy, “Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter,” Vibroengineering Procedia, Vol. 43, pp. 7–13, Jun. 2022, https://doi.org/10.21595/vp.2022.22703

Publisher
V. Gurskyi, V. Korendiy, P. Krot, R. Zimroz, O. Kachur, and N. Maherus, “On the dynamics of an enhanced coaxial inertial exciter for vibratory machines,” Machines, Vol. 11, No. 1, p. 97, Jan. 2023, https://doi.org/10.3390/machines11010097

Publisher

Cited by

Self-synchronisation of vibration exciters of a biharmonic vibration drive

Nikolay Yaroshevich | Vitalii Puts | Tetyana Yaroshevych | Viktor Martyniuk

(2024)

Substantiation of the methodology for calculating the design of a small-sized hydraulic pulse vibrator

Roman Obertyukh | Andrii Slabkyi | Oleksandr Petrov | Dmytro Bakalets

(2024)

About this article

Received

05 January 2023

Accepted

24 January 2023

Published

11 February 2023

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2023.23175

Keywords

vibration exciter

unbalanced rotor

dynamic characteristics

single-mass oscillatory system

dynamic diagram

numerical modeling

simulation

kinematic parameters

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 25

Kinematic analysis and geometrical parameters justification of a planetary-type mechanism for actuating an inertial vibration exciter

Vitaliy Korendiy, Oleh Parashchyn, Volodymyr Heletiy, Viacheslav Pasika, Volodymyr Gurey, Nadiia Maherus

Research article

2023 10 20

Generating rectilinear, elliptical, and circular oscillations of a single-mass vibratory system equipped with an enhanced twin crank-type exciter

Vitaliy Korendiy, Oleksandr Kachur, Rostyslav Predko, Oleh Kotsiumbas, Rostyslav Stotsko, Mykola Ostashuk

Research article

2023 02 11

Dynamics of a wheeled robot driven by an unbalanced rotor and equipped with the overrunning clutches

Vitaliy Korendiy, Oleksandr Kachur, Volodymyr Gurey, Igor Kuzio, Tetyana Hurey, Oleksandr Havrylchenko

Research article

2022 10 22

Simulation and experimental investigation of kinematic characteristics of the wheeled in-pipe robot actuated by the unbalanced rotor

Vitaliy Korendiy, Oleksandr Kachur, Volodymyr Gurey, Rostyslav Predko, Roman Palash, Oleksandr Havrylchenko

O. Kachur, V. Korendiy, O. Lanets, R. Kachmar, I. Nazar, and V. Heletiy, “Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter,” Vibroengineering PROCEDIA, Vol. 48, pp. 8–14, Feb. 2023, https://doi.org/10.21595/vp.2023.23175

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23175
UR  - https://doi.org/10.21595/vp.2023.23175
TI  - Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter
T2  - Vibroengineering PROCEDIA
AU  - Kachur, Oleksandr
AU  - Korendiy, Vitaliy
AU  - Lanets, Oleksii
AU  - Kachmar, Roman
AU  - Nazar, Ihor
AU  - Heletiy, Volodymyr
PY  - 2023
DA  - 2023/02/11
PB  - JVE International Ltd.
SP  - 8-14
VL  - 48
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Kachur_2023,
	doi = {10.21595/vp.2023.23175},
	url = {https://doi.org/10.21595/vp.2023.23175},
	year = 2023,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {48},
	pages = {8--14},
	author = {Oleksandr Kachur and Vitaliy Korendiy and Oleksii Lanets and Roman Kachmar and Ihor Nazar and Volodymyr Heletiy},
	title = {Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]O. Kachur, V. Korendiy, O. Lanets, R. Kachmar, I. Nazar, and V. Heletiy, “Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter,” Vibroengineering PROCEDIA, vol. 48, pp. 8–14, Feb. 2023, doi: 10.21595/vp.2023.23175.

Copy IEEE

Copied to clipboard!

Kachur, Oleksandr, Vitaliy Korendiy, Oleksii Lanets, Roman Kachmar, Ihor Nazar, and Volodymyr Heletiy. “Dynamics of a Vibratory Screening Conveyor Equipped with a Controllable Centrifugal Exciter.” Vibroengineering PROCEDIA 48 (February 11, 2023): 8–14. https://doi.org/10.21595/vp.2023.23175.

Copy Chicago

Copied to clipboard!

Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

Abstract

Highlights

1. Introduction

2. Research methodology

2.1. 3D-model of the vibratory screening conveyor and the enhanced centrifugal exciter

2.2. Dynamic diagram and mathematical model of the conveyor’s oscillatory system

3. Results and discussion

3.1. Numerical modeling of the system oscillations in the Mathematica software

3.2. Simulation of the conveyor operation in the SolidWorks software

4. Conclusions

References

Cited by

About this article

Related Articles