Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter

Korendiy, Vitaliy; Gurey, Volodymyr; Borovets, Volodymyr; Kotsiumbas, Oleh; Lozynskyy, Vasyl

doi:10.21595/vp.2022.22703

Vibroengineering Procedia

Browse Procedia

Published: 13 June 2022

Check for updates

Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter

Vitaliy Korendiy¹

Volodymyr Gurey²

Volodymyr Borovets³

Oleh Kotsiumbas⁴

Vasyl Lozynskyy⁵

^{1, 2, 3}Department of Robotics and Integrated Mechanical Engineering Technologies, Lviv Polytechnic National University, Lviv, Ukraine

⁴Department of Motor Vehicle Transport, Lviv Polytechnic National University, Lviv, Ukraine

⁵Department of Electronics and Information Technology, Lviv Polytechnic National University, Lviv, Ukraine

Corresponding Author:

Vitaliy Korendiy

Cite the article Download PDF

Downloads 324

CrossRef Citations 5

Abstract

Vibration exciters are of the most important parts of vibratory technological equipment. Among a great variety of exciters, the inertial ones are currently the most widely used due to their design simplicity, well-studied control techniques, and relatively large efficiency. The present paper deals with a prospective type of inertial exciters based on a planetary mechanism. The main purpose of this research consists in substantiating the possibilities of providing triangular, rectangular, hexagonal, and other paths of oscillations of a single-mass vibratory system driven by a symmetric planetary-type vibration exciter. The mathematical model of the system motion is developed using the Euler-Lagrange equations, and the following numerical modeling is carried out with the help of the Runge-Kutta methods integrated in the Mathematica software. Virtual experiments are conducted in the SolidWorks software using the 3D-model of the vibratory system. The obtained results are presented in the form of time response curves and motion paths of the oscillating body under different operational conditions. The major scientific novelty of the paper consists in substantiating the parameters of the symmetric planetary-type vibration exciter allowing for generating triangular, rectangular, hexagonal oscillations of the single-mass vibratory system. The obtained results can be effectively used while designing new and improving existent vibratory technological equipment, e.g., conveyors, screens, feeders, sieves, etc.

Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter

Highlights

The possibilities of providing triangular, rectangular and hexagonal paths of oscillations of a single-mass vibratory system with a symmetric planetary-type vibration exciter are substantiated.
The mathematical model of the system motion is developed and the following numerical modeling is carried out in the Mathematica software. Virtual experiments are conducted in the SolidWorks software.
The obtained results are presented in the form of time response curves and motion paths of the oscillating body under different operational conditions.
The parameters of the symmetric planetary-type vibration exciter allowing for generating triangular, rectangular, hexagonal oscillations of the single-mass vibratory system are considered.

1. Introduction

Vibratory technological equipment is widely used in various industries in order to efficiently perform the conveying, feeding, screening, sieving, compacting, polishing, and a wide range of other technological operations. In order to improve the operational efficiency of vibratory machines, numerous researchers and designers work out the possibilities of developing the enhanced excitation mechanisms. Among a great variety of vibration exciters, the inertial ones are currently of the most widely used due to their design simplicity, well-studied control techniques and relatively large efficiency [1]-[5]. In order to provide the controllable motion paths of the vibratory equipment working members, the multi-motor drives are sometimes used. For example, the paper [1] investigates the possibilities of changing the vibration direction angle of the elliptical vibrating screen driven by two motors. The rectilinear oscillations of the five-mass vibratory system excited by two counter-rotating unbalanced rotors are studied in [2]. The dynamic behavior of the vibratory machine equipped with the eccentric self-regulating unbalanced rotor and driven by an induction motor is investigated in [3]. The paper [4] presents the motion equations of the single-, double- and three-mass vibratory systems performing rectilinear oscillations excited by passive auto-balancers. In [5], the authors studied the dynamics of the vibration machine excited by an unbalanced rotor driven by an electric motor with limited power.

On the other hand, the operational efficiency of the vibratory technological equipment can be significantly improved by implementing the planetary-type inertial vibration exciters [6]-[11]. The paper [6] analyses the dynamics and substantiates the occurrence of the self-resonance operational conditions of the symmetric planetary-type vibration exciter. In [7], the author proposed the enhanced design of the vibration exciter allowing for generating the rectilinear (directed) oscillations. The planetary-type adjustable exciter with two unbalanced rotors synchronized by the chain transmission is studied in [8]. The paper [9] is dedicated to investigating the operational conditions of the self-regulating unbalanced rotor used for exciting oscillations of vibration machines with changeable technological load. The dynamic and efficiency parameters of the asymmetric planetary-type vibrations exciters are thoroughly investigated in [10] and [11].

Considering numerous scientific publications related with inertial exciters, in particular, those [1]-[11] mentioned above, it can be concluded that the problems of implementing the planetary-type exciters for providing the controllable kinematic and dynamic parameters of the vibratory equipment are not thoroughly investigated. Therefore, the present paper continues the authors’ previous investigations presented in [12]-[14] and devoted to improving the controllable vibration exciters able to ensure the efficient operation of various vibratory equipment under the changeable loading conditions. The major scientific novelty of the paper consists in substantiating the parameters of the symmetric planetary-type vibration exciter allowing for generating triangular, rectangular, hexagonal, and other paths of oscillations of the single-mass vibratory system.

2. Research methodology

2.1. Dynamic diagrams of vibratory systems with symmetric planetary-type exciters

Let us consider the single-mass vibratory system able to oscillate in two mutually perpendicular directions (Fig. 1). The system is set into motion due to the action of the inertial forces upon the oscillating body. These forces arise when the planet gear rolls on the outside of the sun gear pitch circle, or on the inside of the ring (annual) gear pitch circle (see Fig. 1). In the considered cases, the corresponding sun gear or ring gear is fixed to the oscillating body. The driving motor shaft is located at the hinge O and rotates the carrier OD in clockwise direction. Considering the symmetric planetary-type vibration exciter, the distance AO is equal to the pitch circle radius $R_{1}$ of the corresponding fixed gear. If the radius of the planet gear pitch circle is denoted as $R_{2}$ , the length $l_{O D}$ of the carrier OD can be determined as $l_{O D} = R_{1} \pm R_{2}$ , where the “plus” sign is used in the case of the fixed sun gear, and the “minus” sign is applied when the ring gear is fixed to the oscillating body. The mass of the oscillating body is equal to $m_{1}$ , whilst $m_{2}$ , $m_{3}$ denote the masses of the planet gear and the additional disturbing body rigidly connected with the planet gear at the distance $l_{D E} = R_{3}$ from the hinge D.

Fig. 1Dynamic diagrams of the single-mass vibratory systems with planetary-type exciters

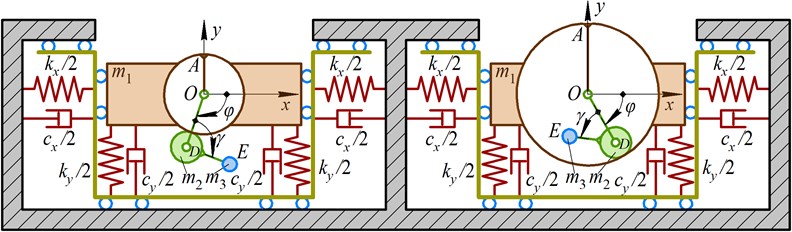
The oscillating body performing the periodic plane-parallel motion is restrained by the system of horizontal and vertical spring-damper elements characterized by the corresponding stiffness and damping coefficients $k_{x}$ , $c_{x}$ , $k_{y}$ , $c_{y}$ . If the direction of the carrier OD rotation is characterized by the angle $φ$ and is considered to be clockwise, the direction of the planet gear and the disturbing body rotation around the hinge D depends on the exciter type: with fixed sun gear or with fixed ring gear. The corresponding directions are defined in Fig. 1 by the angle $γ$ that can be determined by the following expression: $γ = γ_{0} + φ ∙ R_{1} / R_{2}$ .

2.2. Mathematical model describing the system motion

Considering the angle $φ$ as a controllable parameter, let us use the coordinate system $x O y$ to define the hinge O position in a vertical plane. In this case, the hinge O is assumed to be coincident with the oscillating body’s mass center. Therefore, it is enough to adopt two generalized coordinates $x$ , $y$ to uniquely describe the system motion. Using the Euler-Lagrange equations, the mathematical model of the system dynamics can be derived as follows:

1

(m_{1} + m_{2} + m_{3}) ∙ \ddot{x} + c_{x} ∙ \dot{x} + k_{x} ∙ x = (m_{2} + m_{3}) (R_{1} + k ∙ R_{2}) ({\dot{φ}}^{2} ∙ \cos φ + \ddot{φ} ∙ \sin φ) - \frac{m_{3} ∙ R_{3} ∙ (k ∙ R_{1} + R_{2})}{R_{2}} ∙ (\frac{{\dot{φ}}^{2} ∙ (k ∙ R_{1} + R_{2})}{R_{2}} \cos (φ + k (γ_{0} + \frac{R_{1}}{R_{2}} φ)) + \ddot{φ} ∙ \sin (φ + k (γ_{0} + \frac{R_{1}}{R_{2}} φ))),

2

(m_{1} + m_{2} + m_{3}) ∙ \ddot{y} + c_{y} ∙ \dot{y} + k_{y} ∙ y = (m_{2} + m_{3}) (R_{1} + k ∙ R_{2}) ({\dot{φ}}^{2} ∙ \sin φ - \ddot{φ} ∙ \cos φ) + \frac{m_{3} ∙ R_{3} ∙ (k ∙ R_{1} + R_{2})}{R_{2}} ∙ (\frac{{\dot{φ}}^{2} ∙ (k ∙ R_{1} + R_{2})}{R_{2}} \sin (φ + k (γ_{0} + \frac{R_{1}}{R_{2}} φ)) - \ddot{φ} ∙ \cos (φ + k (γ_{0} + \frac{R_{1}}{R_{2}} ∙ φ))),

where $k$ is the coefficient defining the type of the planetary gear mechanism: $k =$ 1 in the case of the fixed sun gear; $k =$ –1 when the ring gear is fixed to the oscillating body.

2.3. Simulation model of the vibratory system developed in the SolidWorks software

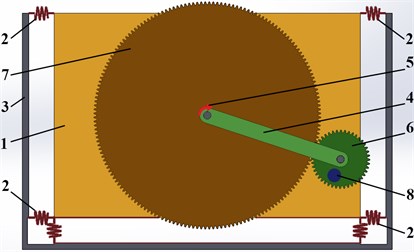
In order to carry out the virtual experiments aimed at analyzing the correctness of the derived mathematical model, the corresponding 3D-design of the vibratory system is developed in the SolidWorks software (see Fig. 2). The system consists of the oscillating body 1 suspended from the unmovable base 3 by the spring-damper elements 2. The carrier (crank) 4 is set into motion by the motion drive 5, and uniformly rotates around the horizontal axis fixed in the mass center of the oscillating body 1. The planet gear 6 rolls on the outside of the sun gear 7 that is connected to the body 1. The unbalanced (disturbing) mass 8 is fixed on the planet gear 6.

Fig. 2Simulation model of the vibratory system equipped with the planetary-type exciter

3. Results and discussion

3.1. Numerical modeling of the system motion in the Mathematica software

Let us consider the case of steady-state oscillations of the vibratory system equipped with the symmetric planetary-type vibration exciter in which the sun gear is fixed ( $k = 1$ ). The forced frequency is constant: $ω =$ 157 rad/s. Therefore, the motion of the carrier is performed according to the following law: $φ = φ_{0} + ω ∙ t$ . To carry out further numerical modeling, the following input parameters are introduced: $φ_{0} =$ 0, $γ_{0} =$ 3.14, $m_{1} =$ 30 kg, $R_{1} =$ 0.088 m, $R_{3} =$ 0.04 m, $k_{x} = k_{y} =$ 3∙10⁶ N⁄m, $c_{x} = c_{y} =$ 100 (N∙s)/m. The masses $m_{2}$ , $m_{3}$ , and radius $R_{2}$ are considered as controllable parameters defining the paths (trajectories) of the oscillating body.

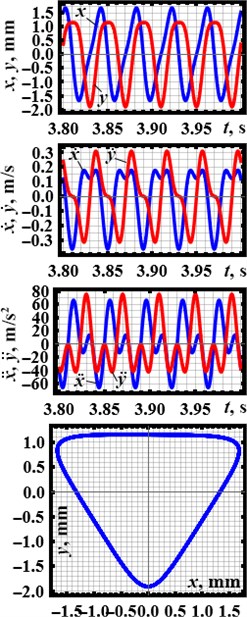
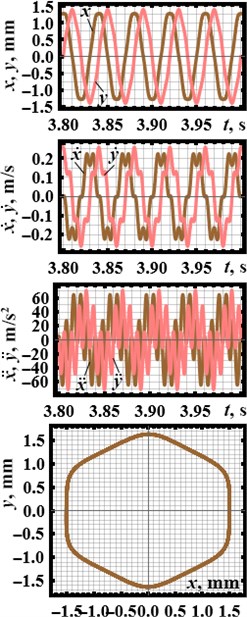
The results of numerical modeling (Fig. 3) are presented in the form of time dependencies of the basic kinematic characteristics of the system motion: horizontal and vertical displacements, velocities, accelerations. In addition, the motion paths (trajectories) of the oscillating body are plotted under different inertial and geometric parameters of the planetary-type vibration exciter. For example, the triangular path of the body oscillations is obtained at: $m_{2} =$ 0.8 kg, $m_{3} =$ 0.03 kg, $R_{2} =$ 0.088 m (Fig. 3(a)). The rectangular path is observed at: $m_{2} =$ 1.1 kg, $m_{3} =$ 0.08 kg, $R_{2} =$ 0.044 m (Fig. 3(b)). The hexagonal path is drawn at: $m_{2} =$ 1.3 kg, $m_{3} =$ 0.04 kg, $R_{2} =$ 0.022 m (Fig. 3(c)). The corresponding analytical relations between inertial and geometric parameters of the symmetric planetary-type vibration exciter providing certain motion paths of the oscillating body will be derived in further investigations. In the present paper, let us consider the kinematic characteristics of the body at the mentioned parameters.

Fig. 3Kinematic characteristics of the system motion at different design parameters of the planetary-type vibration exciter: a) m2= 0.8 kg, m3= 0.03 kg, R2= 0.088 m; b) m2= 1.1 kg, m3= 0.08 kg, R2= 0.044 m; c) m2= 1.3 kg, m3= 0.04 kg, R2= 0.022 m

Kinematic characteristics of the system motion at different design parameters of the planetary-type vibration exciter: a) m2= 0.8 kg, m3= 0.03 kg, R2= 0.088 m; b) m2= 1.1 kg, m3= 0.08 kg, R2= 0.044 m; c) m2= 1.3 kg, m3= 0.04 kg, R2= 0.022 m

a)

b)

c)

All the motion paths considered above (triangular, rectangular, hexagonal) are characterized by the largest horizontal and vertical displacements (swings, peak-to-peak values) of about 3 mm. The oscillating body’s horizontal and vertical speeds vary in the range of –0.35,…, 0.35 m/s, while the accelerations change within –80,…, 80 m/s². All the characteristic differences between displacements, velocities and accelerations of the oscillating body at different inertial and geometric parameters of the planetary-type vibration exciter can be observed in Fig. 3.

3.2. Simulation of the system motion in the SolidWorks software

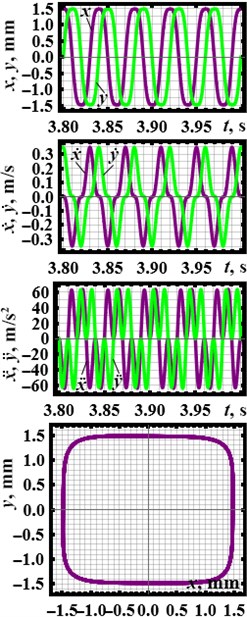
Applying the same geometric, inertial, damping, and stiffness parameters of the vibratory system as the ones used for carrying out numerical modeling, let us conduct virtual experiments of the system motion in the SolidWorks software. The obtained simulation results are presented in Fig. 4. The starting (transient, unsteady) conditions lasts about 1,…, 1.5 s. Under the steady-state oscillations, the rectangular and hexagonal motion paths of the body, as well as its other kinematic characteristics satisfactorily agree with the ones obtained by numerical modeling.

Fig. 4Kinematic characteristics of the system motion simulated in the SolidWorks software at different design parameters of the planetary-type vibration exciter: a) m2= 1.1 kg, m3= 0.08 kg, R2= 0.044 m; b) m2= 1.3 kg, m3= 0.04 kg, R2= 0.022 m

Kinematic characteristics of the system motion simulated in the SolidWorks software at different design parameters of the planetary-type vibration exciter: a) m2= 1.1 kg, m3= 0.08 kg, R2= 0.044 m; b) m2= 1.3 kg, m3= 0.04 kg, R2= 0.022 m

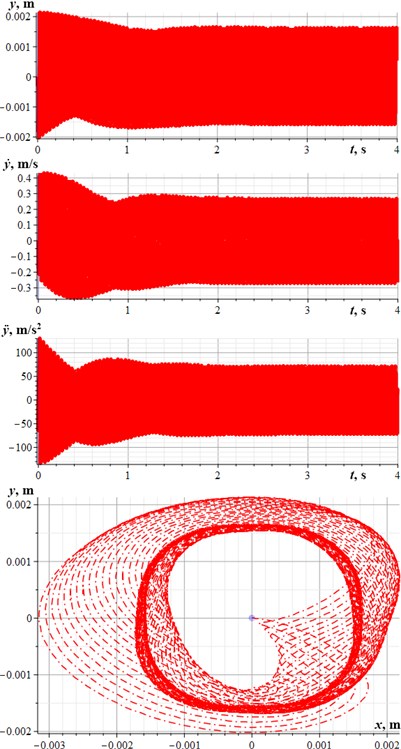
a)

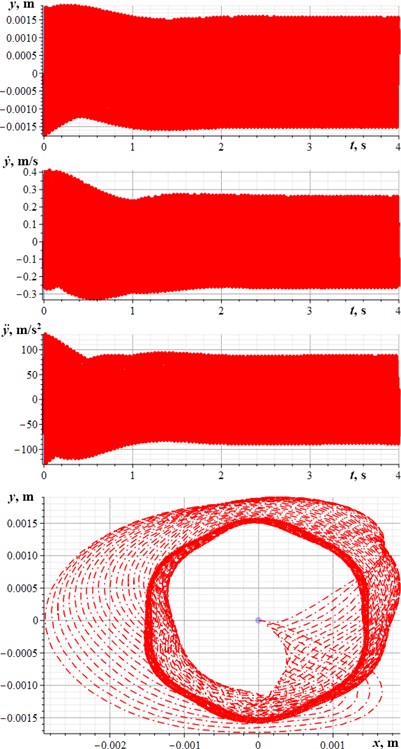
b)

4. Conclusions

The paper studies the dynamics of the single-mass vibratory system equipped with the symmetric planetary-type vibration exciter. The mathematical model of the system motion is derived. The results of numerical modeling performed in the Mathematica software satisfactorily agree with the simulation results obtained in the SolidWorks software. The starting conditions lasts 1,…, 1.5 s. Under the steady-state oscillations of the body, the triangular path is obtained at: $m_{2} =$ 0.8 kg, $m_{3} =$ 0.03 kg, $R_{2} =$ 0.088 m; the rectangular path – at: $m_{2} =$ 1.1 kg, $m_{3} =$ 0.08 kg, $R_{2} =$ 0.044 m; the hexagonal path – at: $m_{2} =$ 1.3 kg, $m_{3} =$ 0.04 kg, $R_{2} =$ 0.022 m. All the motion paths are characterized by the largest horizontal and vertical displacements of about 3 mm. The oscillating body’s horizontal and vertical speeds vary in the range of –0.35,…, 0.35 m/s, while the accelerations change within –80,…, 80 m/s². The obtained results can be effectively used while designing new and improving existent vibratory technological equipment, e.g., conveyors, screens, feeders, sieves, polishing machines, compactors, etc.

References

B. Chen, J. Yan, Z. Yin, and K. K. Tamma, “A new study on dynamic adjustment of vibration direction angle for dual-motor-driven vibrating screen,” Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, Vol. 235, No. 2, pp. 186–196, Apr. 2021, https://doi.org/10.1177/0954408920952603

Publisher
W. Hu, X. Zhang, W. Zhang, W. Chen, and S. Cui, “Stability and motion characteristics in a vibrating system with five rigid frames driven by two counter-rotating exciters,” Journal of Low Frequency Noise, Vibration and Active Control, Vol. 40, No. 4, pp. 1780–1794, Dec. 2021, https://doi.org/10.1177/14613484211019643

Publisher
V. M. Shatokhin, V. N. Sobol, W. Wуjcik, G. Duskazaev, and D. Jarykbassov, “Dynamical processes simulation of unbalanced vibration devices with eccentric rotor and induction electric drive,” PRZEGLĄD ELEKTROTECHNICZNY, Vol. 1, No. 4, pp. 81–87, Apr. 2019, https://doi.org/10.15199/48.2019.04.14

Publisher
V. Yatsun, G. Filimonikhin, K. Dumenko, and A. Nevdakha, “Equations of motion of vibration machines with a translational motion of platforms and a vibration exciter in the form of a passive auto-balancer,” Eastern-European Journal of Enterprise Technologies, Vol. 5, No. 1 (89), pp. 19–25, Oct. 2017, https://doi.org/10.15587/1729-4061.2017.111216

Publisher
N. Yaroshevich, O. Yaroshevych, and V. Lyshuk, “Drive dynamics of vibratory machines with inertia excitation,” Mechanisms and Machine Science, Vol. 95, pp. 37–47, 2021, https://doi.org/10.1007/978-3-030-60694-7_2

Publisher
R. Palevičius and K. Ragulskis, “The self-resonance effect of the planetary vibration excitation systems,” Journal of Vibroengineering, Vol. 14, No. 1, pp. 244–249, 2012.

Search CrossRef
V. V. Mikheyev, “New type of vibration generator with vibratory force oriented in preferred direction,” Journal of Vibration Engineering and Technologies, Vol. 6, No. 2, pp. 149–154, Apr. 2018, https://doi.org/10.1007/s42417-018-0025-4

Publisher
V. V. Mikheyev and S. V. Saveliev, “Planetary adjustable vibratory exciter with chain gear,” in Journal of Physics: Conference Series, Vol. 1210, No. 1, p. 012097, Mar. 2019, https://doi.org/10.1088/1742-6596/1210/1/012097

Publisher
I. Lyan, K. Krestnikovskii, G. Panovko, and A. Shokhin, “Determination of mass-geometric characteristics of self-regulating debalance of an inertial vibration exciter,” Vibroengineering Procedia, Vol. 25, pp. 70–75, Jun. 2019, https://doi.org/10.21595/vp.2019.20810

Publisher
A. Kim, M. Doudkin, A. Ermilov, G. Kustarev, M. Sakimov, and M. Mlynczak, “Analysis of vibroexciters working process of the improved efficiency for ice breaking, construction and road machines,” Journal of Vibroengineering, Vol. 22, No. 3, pp. 465–485, May 2020, https://doi.org/10.21595/jve.2020.20446

Publisher
M. Marek, G. Kustarev, and N. Andrjuchov, “Theoretical studies and conditions analysis of the inertial slider slippage of asymmetric planetary vibration exciter for snowplow,” Bulletin of D. Serikbayev EKTU, No. 3, pp. 63–78, 2021, https://doi.org/10.51885/1561-4212_2021_3_63

Publisher
O. Lanets, O. Kachur, V. Korendiy, and V. Lozynskyy, “Controllable crank mechanism for exciting oscillations of vibratory equipment,” in Lecture Notes in Mechanical Engineering, pp. 43–52, 2021, https://doi.org/10.1007/978-3-030-77823-1_5

Publisher
V. Korendiy, V. Gursky, O. Kachur, V. Gurey, O. Havrylchenko, and O. Kotsiumbas, “Mathematical modeling of forced oscillations of semidefinite vibro-impact system sliding along rough horizontal surface,” Vibroengineering Procedia, Vol. 39, pp. 164–169, Dec. 2021, https://doi.org/10.21595/vp.2021.22298

Publisher
V. Gursky, P. Krot, V. Korendiy, and R. Zimroz, “Dynamic analysis of an enhanced multi-frequency inertial exciter for industrial vibrating machines,” Machines, Vol. 10, No. 2, p. 130, Feb. 2022, https://doi.org/10.3390/machines10020130

Publisher

Cited by

Force analysis of the planetary-type mechanisms of the enhanced vibration exciters

(2024)

On the Dynamics of an Enhanced Coaxial Inertial Exciter for Vibratory Machines

(2023)

Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

(2023)

Generating rectilinear, elliptical, and circular oscillations of a single-mass vibratory system equipped with an enhanced twin crank-type exciter

(2023)

Kinematic analysis and geometrical parameters justification of a planetary-type mechanism for actuating an inertial vibration exciter

(2023)

About this article

Received

14 May 2022

Accepted

29 May 2022

Published

13 June 2022

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2022.22703

Keywords

vibratory technological equipment

planetary mechanism

mathematical model

operational conditions

numerical modeling

3D-model

simulation

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 25

Kinematic analysis and geometrical parameters justification of a planetary-type mechanism for actuating an inertial vibration exciter

Vitaliy Korendiy, Oleh Parashchyn, Volodymyr Heletiy, Viacheslav Pasika, Volodymyr Gurey, Nadiia Maherus

Research article

2023 10 20

Generating rectilinear, elliptical, and circular oscillations of a single-mass vibratory system equipped with an enhanced twin crank-type exciter

Vitaliy Korendiy, Oleksandr Kachur, Rostyslav Predko, Oleh Kotsiumbas, Rostyslav Stotsko, Mykola Ostashuk

Research article

2023 05 18

Analyzing the possibilities of generating the reciprocating motion and plane oscillations of a working member of a vibratory lapping-polishing machine

Vitaliy Korendiy, Viktor Zakharov, Igor Kuzio, Volodymyr Borovets, Oleksandr Havrylchenko, Yaroslav Danylo

Research article

2023 02 11

Dynamics of a vibratory screening conveyor equipped with a controllable centrifugal exciter

Oleksandr Kachur, Vitaliy Korendiy, Oleksii Lanets, Roman Kachmar, Ihor Nazar, Volodymyr Heletiy

V. Korendiy, V. Gurey, V. Borovets, O. Kotsiumbas, and V. Lozynskyy, “Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter,” Vibroengineering PROCEDIA, Vol. 43, pp. 7–13, Jun. 2022, https://doi.org/10.21595/vp.2022.22703

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22703
UR  - https://doi.org/10.21595/vp.2022.22703
TI  - Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter
T2  - Vibroengineering PROCEDIA
AU  - Korendiy, Vitaliy
AU  - Gurey, Volodymyr
AU  - Borovets, Volodymyr
AU  - Kotsiumbas, Oleh
AU  - Lozynskyy, Vasyl
PY  - 2022
DA  - 2022/06/13
PB  - JVE International Ltd.
SP  - 7-13
VL  - 43
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Korendiy_2022,
	doi = {10.21595/vp.2022.22703},
	url = {https://doi.org/10.21595/vp.2022.22703},
	year = 2022,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {43},
	pages = {7--13},
	author = {Vitaliy Korendiy and Volodymyr Gurey and Volodymyr Borovets and Oleh Kotsiumbas and Vasyl Lozynskyy},
	title = {Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]V. Korendiy, V. Gurey, V. Borovets, O. Kotsiumbas, and V. Lozynskyy, “Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter,” Vibroengineering PROCEDIA, vol. 43, pp. 7–13, Jun. 2022, doi: 10.21595/vp.2022.22703.

Copy IEEE

Copied to clipboard!

Korendiy, Vitaliy, Volodymyr Gurey, Volodymyr Borovets, Oleh Kotsiumbas, and Vasyl Lozynskyy. “Generating Various Motion Paths of Single-Mass Vibratory System Equipped with Symmetric Planetary-Type Vibration Exciter.” Vibroengineering PROCEDIA 43 (June 13, 2022): 7–13. https://doi.org/10.21595/vp.2022.22703.

Copy Chicago

Copied to clipboard!

Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter

Abstract

Highlights

1. Introduction

2. Research methodology

2.1. Dynamic diagrams of vibratory systems with symmetric planetary-type exciters

2.2. Mathematical model describing the system motion

2.3. Simulation model of the vibratory system developed in the SolidWorks software

3. Results and discussion

3.1. Numerical modeling of the system motion in the Mathematica software

3.2. Simulation of the system motion in the SolidWorks software

4. Conclusions

References

Cited by

About this article

Related Articles