On dynamics of a rigid body moving on a horizontal plane by means of motion of an internal particle

1. Introduction

Investigation of dynamic of rigid body, which moves by means of relative motions of its internal components is a relevant engineering problem. The advantage of the so-called vibrating mobile robots is that they are simple in design, i.e. do not require external elements such as wheels or track chains and can be produced as isolated capsules. This circumstance makes them resistant to aggressive external environment. That is why they can be used both on hard surfaces and in liquids. In papers [1-9] dynamics and control of a rigid body moving on a rough horizontal plane by means of relative motions of the internal components has been studied.

In this paper we consider the mechanical system consisting of a rigid body of mass $M$ and a particle of mass $m$ moving inside the body in a circle of radius $R$. The center of the circle is located in the body mass center and the angular velocity $\omega$ of the relative circular motion of the particle is a constant.

Fig. 1Coordinate systems

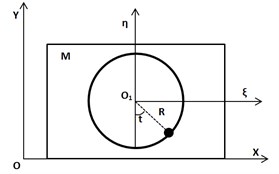
We consider a rectilinear translation of the body in a rough horizontal plane. In this case the position of the body can be defined by one variable $X$, which is the X-coordinate of its center of mass in fixed coordinate system OXY (see Fig.1).

Let us introduce dimensionless time $t$ so that the period of particle relative motion is equal to $2\pi$. Without loss of generality we suppose that at moment $t$= 0 the particle, moving counterclockwise, passes the lowest point of the circle. Then the time $t$ can be regarded as angle defining the position of the particle in moving (with the body) coordinate system O₁ξη (see Fig. 1).

Taking into account gravity and dry friction forces we have the following equation of motion [7]:

where:

and $u=dx/dt$. The dimensionless coordinate $x$ and the parameter $\mu$, are introduced by formulas:

where $g$ is the gravitational acceleration, $k$ is the coefficient of dry friction.

We also assume that the body can start moving from state of rest, i.e. $k^2\le 1/({\mu }^2-1)$ as well as the body moves without jumps on the horizontal plane, i.e. $\mu \ge 1$. In [7] the partial solution of Eq. (1) with initial condition $u\left(0\right)=0$ has been studied in detail for all possible parameters values. In this paper we study solutions of Eq. (1) with arbitrary initial conditions. In Sections 3 and 4 we show that the above partial solution plays an important role in dynamics of the system considered. In particular, it has properties of a limit cycle.

2. Zones of friction deceleration and periodic motions

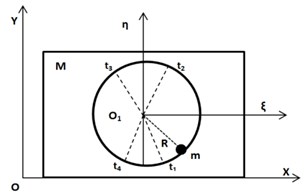
First we note that at $u\left(t\right)\ne 0$ the right hand side of Eq. (1) is equal to zero at the moments of time, when the horizontal component of inertia force applied to the particle and the dry friction force have opposite directions, but their absolute values are equal. In the interval [0;$2\pi$] such moments of time can be calculated as follows [7]:

The positions of the particle corresponding to the moments $t_1,t_2,t_3,t_4$are shown in Fig. 2. In the intervals $\left(t_2,t_3\right)$ and $(t_4,t_1)$ direction of the body’s acceleration is opposite to the velocity of the body. The above intervals we call upper and lower zones of friction deceleration respectively. They play a significant role for the analysis of the body motion. In particular, if the body stops, when the particle is in one of them, then the body remains at rest until the particle leaves the zone of friction deceleration. This phenomenon we call the body sticking.

Fig. 2Zones of friction deceleration

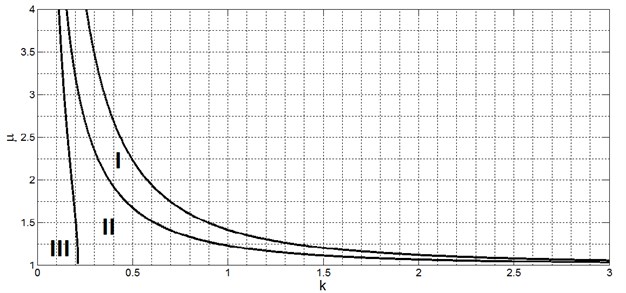
It was shown in [7] that for any possible values of parameters $k$ and $\mu$ there exists motion of body with $2\pi$-periodically changing velocity. Depending on the parameters such a periodic motion can have a quite different nature. The area of possible values of parameters $k$ and $\mu$ is separated into three domains I, II and III corresponding to different types of the periodic motions (see Fig. 3).

Domain I is defined by the following inequalities:

In domain I the solution of Eq. (1) with initial condition $u\left(t_1\right)=0$ is periodic. This solution describes the motion of the body with stops both in the upper and in the lower zones of friction deceleration. Moreover, the coordinate $x\left(t\right)$ is also a $2\pi$-periodic function in this case.

Domain II is defined by inequalities:

In this domain the solution of Eq. (1) with initial condition $u\left(t_1\right)=0$ is also $2\pi$-periodic. However, the coordinate $x\left(t\right)$ is not periodic function in this case. The body moves with a stop only in the lower zone of friction deceleration such that $x\left(t+2\pi \right)-x\left(t\right)>0$.

Domain III is defined by the inequalities:

In domain III the solution of Eq. (1) with initial condition $u\left(t_1\right)=0$ is not periodic, but it approaches a periodic limit cycle, which describes motion of the body without stopping in any zones of friction deceleration.

Fig. 3Domains of periodic motion; horizontal axis – k, vertical axis – μ

3. Motion of the body in domains I and II

Let the parameters belong to domain I. Consider the solution of Eq. (1) with initial condition $u\left(t_1\right)=u_1$, where $u_1$ is a real positive number. For positive velocity $u$ the Eq. (1) reads:

That is:

Eq. (9) describes the motion of the body until the velocity $u$ is positive, i.e. the motion in the interval [${t_1,t}^{\text{'}}$], where $u\left(t^{\text{'}}\right)=0$. It can be shown that $\sin t-k\left(\mu +\cos t\right)>0$ in the interval [$t_1,t_2$] and $\sin t-k\left(\mu +\cos t\right)<0$ in the interval [$t_2;t_1+2\pi$]. It means that, function $u\left(t\right)$ increases in the interval [$t_1,t_2$] and decreases in the interval [$t_2;t_1+2\pi$].

On the other hand, from Eq. (9) we have:

Thus, if $u_1>2\pi k\mu$, then in the interval [$t_1;t_1+2\pi$] the body moves in positive direction without stopping. The velocity of the body decreases by $2\pi k\mu$ for the period $2\pi$.

Let us now suppose that $u_1<2\pi k\mu$. In this case the body stops in the interval [$t_2;t_1+2\pi$], i.e. $t^{\text{'}}<t_1+2\pi$. Note that $t^{\text{'}}>t_2$, because function $u\left(t\right)$ increases in the interval [$t_1,t_2$].

If the body stops in the upper or in the lower zone of friction deceleration, then it remains at rest till the moment $t_3$ or $t_1+2\pi$ respectively. In both cases $u\left(t_1+2\pi \right)=0$, that is for $t>t^{\text{'}}$ the body moves with $2\pi$-periodically changing velocity.

It remains to consider the case when the body stops in the interval [$t_3,t_4$]. Thus, we suppose that $t_3{<t}^{\text{'}}<t_4$ and consider the motion of the body for $t>t^{\text{'}}$. In this case Eq. (1) takes the following form:

That is:

It can be shown that $\sin t+k\left(\mu +\cos t\right)<0$ in the interval $\left[t_3,t_4\right]$ and $\sin t+k\left(\mu +\cos t\right)>0$ in the interval [$t_4;t_1+2\pi$]. It means, that function $u\left(t\right)$ defined by Eq. (11) decreases in the interval [$t^{\text{'}},t_4$] and increases in the interval [$t_4;t_1+2\pi$]. Thus, after the stop at the moment $t=t^{\text{'}}$ the body starts to move in opposite direction, i.e. with negative velocity until it stops again at some moment $t=t^{\text{'}\text{'}}>t_4$. By using Eq. (12) and taking in to account the condition $u\left(t^{\text{'}\text{'}}\right)=0$ we have:

On the other hand, there exists the periodic motion in domain I such that at the moment $t=t_3$ the body starts to move in negative direction of axis OX and stops in lower zone of friction deceleration at the moment $t=t_{**}$, where $t_4<t_{**}<t_1+2\pi$, (see [7] for more details). For such a motion we have $u\left(t_3\right)=u\left(t_{**}\right)=0$. Taking this fact into account by analogy with Eq. (13) we have:

Now we recall that $\sin t+k\left(\mu +\cos t\right)<0$ in the interval [$t_3,t_4$], that is why:

By taking into account Eqs. (13), (14) we can rewrite the inequality (15) in the following form:

Since $\sin t+k\left(\mu +\cos t\right)>0$ in the interval [$t_4;t_1+2\pi$], it follows from Eq. (16) that $t^{\text{'}\text{'}}$<$t_{**}<t_1+2\pi$, i.e. the body stops in the lower zone of friction deceleration and remains at rest till the moment $t_1+2\pi$. That is, for $t>t_1$ the body moves with $2\pi$-periodically changing velocity.

Thus, if the body starts to move with positive velocity, then it always passes in periodic mode of motion for a finite period of time. It is easy to see that the same result takes place in the case of negative initial velocity.

By analogy it can be also shown that in domain II the motion of the body has similar properties.

4. Motion of the body in domain III. Stability of periodic motion

Let us suppose that the parameters belong to domain III. In this case there exists a periodic mode of motion such that the body stops and reverses its direction of motion twice in the period$2\pi$ [7]. The stops of the body take place outside of both upper and lower zone of friction deceleration. That is the sticking phenomenon does not take place and there exists two moments of time $t_1^{*}\in [t_1;t_2]$ and $t_2^{*}\in [t_3;t_4]$, such that $u\left(t_1^{*}\right)=u\left(t_2^{*}\mathrm{}\right)=0$. The values $t_1^{*}$ and $t_2^{*}$ satisfy the following system of equations [7]:

It is clear that if values $t_1^{*}$ and $t_2^{*}$ are found, than the periodic mode of motion is fully determined. Numerical investigations have shown that in domain III the above system of Eq. (17) has a unique solution.

In order to prove the asymptotic stability of the above periodic mode of motion, we consider solution of Eq. (1) with the initial condition $u\left(t_1^{*}\right)=\epsilon$, where $\epsilon$ is a small value. Without loss of generality we assume that $\epsilon >0$. We will construct such a solution by integrating Eq. (1) in finite intervals of time, where the velocity of the body keeps a definite direction, i.e. the function $u\left(t\right)$ does not change sign within these intervals.

At the first step we integrate Eq. (1) with the initial condition $u\left(t_1^{*}\right)=\epsilon$ in the interval $\left(t_1^{*},t_2^{*}+\tau \right)$, where value $\tau$ satisfies the condition $u\left(t_2^{*}+\tau \right)=0$. As a result, we have:

Let us expand the left hand side of Eq. (18) in a power series in $\tau$:

By solving Eq. (19) with respect to $\tau$, we have:

At the second step by integrating Eq. (1) in the interval $(t_2^{*}+\tau ,t_1^{*}+2\pi )$ with the initial condition $u\left(t_2^{*}+\tau \right)=0$, we get:

Now we expand left and right hand side of Eq. (21) in a power series in $\tau$:

By substituting Eq. (20) in Eq. (22), we get:

Consider the expression:

First, we note that $k\left(\mu +\cos t_2^{*}\right)>0$, because we have supposed $\mu >1$. Then, we recall that $t_2^{*}\in [t_3;t_4]$, hence $\sin t_2^{*}<0$. Now it is easy to see that the following inequality holds:

The last inequality can be rewritten in the form:

The process of integration of Eq. (1) can be continued. Finally, we get the following asymptotic estimate:

It follows from Eq. (27) that $u(t_1^{*}+2\pi n)\to 0$ as $n\to \infty$, i.e. the solution with the initial condition $u\left(t_1^{*}\right)=\epsilon$ approaches the periodic solution with the initial condition $u\left(t_1^{*}\right)=0$ at $t\to \infty$. It means that the above periodic solution is asymptotically stable.

5. Conclusions

In this paper an analytical study of dynamics of a rigid body with a moving internal particle is performed. The body moves on a rough horizontal plane without jumps. It appears that for any possible parameter values there exists a periodic mode of motion, which is a limit cycle. The above periodic mode is asymptotically stable. The stability has global character, i.e. for all initial conditions the motion of the body approaches the periodic mode. Depending on parameters a finite or infinite period of time is necessary to pass into the periodic mode of motion.