On the analysis of forced oscillations of systems with two random sources of parametric effects

Roev, Boris; Vinokur, Aleksey

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

On the analysis of forced oscillations of systems with two random sources of parametric effects

Boris Roev¹

Aleksey Vinokur²

^{1, 2}Moscow State University of Printing Arts, Moscow, Russia

²National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russia

Corresponding Author:

Boris Roev

Cite the article Download PDF

Downloads 1379

Abstract

The problem of forced oscillations in a mechanical system with random parameters is considered in this paper. The analysis of the interaction of forced and parametric oscillators is conducted by the example of the system where the properties of inertia and stiffness are randomized. The parametric effects are presented in the form of narrowband random processes. The obtained amplitude-frequency characteristics demonstrate the development of dynamic processes.

1. Introduction

When considering a number of machines, in particular the printing ones, the relevant issue is the interaction of parametric and forced random oscillations that occur in them. Problems of this kind in general terms were studied in [1-6].

We demonstrate the results of the interaction of forced and parametric random oscillations study by the example of the system performing torsion oscillations, when the coefficients of the inertial term and the stiffness-related term change randomly. The equation Eq. (1) describing these oscillations is as follows:

1

(1 - f_{1} (t)) \ddot{θ} + 2 ε \dot{θ} + ω_{0}^{2} (1 - f_{3} (t)) θ = m (t),

where $θ (t)$ – angle of rotation $f_{j} (t)$ – parametric effects, $m (t)$ – equivalent rotational moment; $ε$ , $ω_{0}$ – the system parameters [4]; the description of inciting factors $f_{j} (t)$ and $m (t)$ is presented hereafter.

2. The method

To solve the problem, we use a modified spectral method [7, 8]. For functions $θ (t)$ $f_{j} (t)$ we introduce the following integral representations Eq. (2):

2

θ (t) = θ_{0} (t) + \int_{- \infty}^{\infty} ψ (ω, t) Q (ω) e^{i ω t} d ω,

f_{j} (t) = \int_{- \infty}^{\infty} F_{j} (ω) e^{i ω t} d ω, j = 1,3,

where $θ_{0} (t)$ – the expected rotation angle of $θ (t)$ ; $ψ (ω, t)$ – an unknown deterministic function; $Q (ω)$ and $F_{j} (ω)$ – random spectra that satisfy the conditions of stochastic orthogonality. The external action is deterministic and is presented as: $m (t) = m_{0} \cos Ω t$ .

After substituting Eq. (2) into Eq. (1) and drawing up the torque ratios by the method described in [7, 8], for the unknown function $θ_{0} (t)$ and $ψ (ω, t)$ we obtain the following system of differential equations Eq. (3):

3

{\ddot{θ}}_{0} + 2 ε {\dot{θ}}_{0} + ω_{0}^{2} θ_{0} - \int_{- \infty}^{\infty} [(\ddot{ψ} + 2 i ω \dot{ψ} - ω^{2} ψ) S_{f 1 θ} + ω_{0}^{2} ψ S_{f 3 θ}] d ω = m_{0} c o s Ω t,

[\ddot{ψ} + 2 (ε + i ω) \dot{ψ} + (ω_{0}^{2} - ω^{2} + 2 i ε ω) ψ] S_{f 1 θ} (ω) - {\ddot{θ}}_{0} S_{f 1} (ω) - ω_{0}^{2} θ S_{f 1 f 3} (ω) = 0,

[\ddot{ψ} + 2 (ε + i ω) \dot{ψ} + (ω_{0}^{2} - ω^{2} + 2 i ε ω) ψ] S_{f 3 θ} (ω) - {\ddot{θ}}_{0} S_{f 1 f 3} (ω) - ω_{0}^{2} θ S_{f 3} (ω) = 0 .

Let the parametric effects be the perfect narrow-band processes with spectral densities Eq. (4):

4

S_{f j} (ω) = \frac{σ_{f j}^{2}}{2} δ (ω - ω_{j}),

with the same carrier frequency $ω_{1} = ω_{3} = ω_{*}$ , but with different variance $σ_{f j}^{2}$ . Here $δ (ω)$ is the Dirac delta-function.

Then we find a particular solution of this system which describes the steady-state forced oscillations. Since the right part of the system is $m (t) = m_{0} \cos Ω t$ , then the solution Eq. (5) will be sought in the following form:

5

θ_{0 *} (t) = A \cos Ω t + B \sin Ω t,

ψ (ω, t) = D (ω) \cos Ω t + G (ω) \sin Ω t .

As a result of the substitution of Eq. (4) and Eq. (5) in Eq. (3) and making the necessary transformations, we obtain a formula for the amplitude of rotation angles Eq. (6):

6

\bar{A} = \sqrt{A^{2} + B^{2}} = \frac{m_{0}}{ω_{0}^{2} {\bar{Δ}}_{1}} \sqrt{{\bar{α}}_{22}^{2} + {\bar{α}}_{21}^{2}},

where:

{\bar{α}}_{11}^{} = 1 - γ^{2} + I_{1}, {\bar{α}}_{12}^{} = (2 δ γ + I_{2}), {\bar{α}}_{21}^{} = (- 2 δ γ + I_{3}), {\bar{α}}_{22}^{} = 1 - γ^{2} + I_{4},

I_{1} = σ_{f 1}^{2} \frac{a_{11} A_{1} + b_{11} B_{1}}{A_{1}^{2} + B_{1}^{2}} + σ_{f 3}^{2} \frac{c_{5} A_{1} + d_{5} B_{1}}{A_{1}^{2} + B_{1}^{2}}, I_{2} = σ_{f 1}^{2} \frac{a_{21} A_{1} + b_{21} B_{1}}{A_{1}^{2} + B_{1}^{2}} + σ_{f 3}^{2} \frac{c_{6} A_{1} + d_{6} B_{1}}{A_{1}^{2} + B_{1}^{2}},

I_{3} = σ_{f 1}^{2} \frac{a_{31} A_{1} + b_{31} B_{1}}{A_{1}^{2} + B_{1}^{2}} + σ_{f 3}^{2} \frac{c_{6} A_{1} + d_{6} B_{1}}{A_{1}^{2} + B_{1}^{2}}, I_{4} = σ_{f 1}^{2} \frac{a_{41} A_{1} + b_{41} B_{1}}{A_{1}^{2} + B_{1}^{2}} + σ_{f 3}^{2} \frac{c_{5} A_{1} + d_{5} B_{1}}{A_{1}^{2} + B_{1}^{2}},

a_{11} = - γ^{2} \cdot (c_{1} + c_{4}), b_{11} = - γ^{2} \cdot (d_{1} + d_{4}), a_{21} = γ^{2} \cdot (c_{2} - c_{3}),

b_{21} = γ^{2} \cdot (d_{2} - d_{3})_{1}, a_{31} = - γ^{2} \cdot (c_{2} + c_{3}), b_{11} = - γ^{2} \cdot (d_{2} + d_{3}),

a_{41} = - γ^{2} \cdot (c_{1} - c_{4}), b_{21} = - γ^{2} \cdot (d_{1} - d_{4}), c_{1} = (γ_{1}^{2} - γ^{2}) (1 - γ^{2} - γ_{1}^{2}),

d_{1} = 2 δ γ_{1} (γ_{1}^{2} - γ^{2}), c_{2} = 2 δ γ (γ_{1}^{2} - γ^{2}), d_{2} = 2 γ γ_{1} (γ_{1}^{2} - γ^{2}),

c_{3} = - 4 δ γ_{1}^{2} γ, d_{3} = 2 γ_{1} γ (1 - γ^{2} - γ_{1}^{2}), c_{4} = - 4 γ_{1}^{2} γ^{2}, d_{4} = 4 δ γ^{2} γ_{1},

c_{5} = 1 - γ^{2} - γ_{1}^{2}, d_{5} = 2 δ γ_{1}, c_{6} = 2 δ γ, d_{6} = 2 γ_{1} γ,

A_{1} = {(1 - γ^{2} - γ_{1}^{2})}^{2} + 4 \cdot (γ^{2} (δ^{2} - γ_{1}^{2}) - δ^{2} γ_{1}^{2}), B_{1} = 4 δ γ_{1} \cdot (1 + γ^{2} - γ_{1}^{2}),

γ = \frac{Ω}{ω_{0}}, γ_{1} = \frac{ω_{*}}{ω_{0}}, δ = \frac{ε}{ω_{0}} .

3. The results

In order to visualize the results of the study, these characteristics must be built into a volumetric image and in the form of level graphic charts. If we record the frequency of the external and the parametric effects in the form of one-dimensional arrays $γ_{i}$ and $γ_{1 j}$ ( $i =$ 1,..., 200; $j =$ 1,..., 300 with a step of 0.02), then the amplitude (6) occurring in the drive system, will be a two-dimensional array ${\bar{A}}_{i j}$ , whose graphical image is a surface. Level graphic charts provide an opportunity to observe a change in the amplitude-frequency characteristics on the frequency plane. In this case the vertical axis corresponds to the frequency of the external effect, and the horizontal axis corresponds to the frequency of the parametric one. Let us consider the effect of the variance $σ_{f 3}^{2}$ of parametric influence, taking only stiffness, while considering that the inertia effect is absent $σ_{f 1}^{2} = 0$ . In this case the dimensionless damping parameter was taken as $δ =$ 0.2. First, let us consider the case when $σ_{f 3}^{2} = 0$ . Then the amplitude-frequency response will correspond to the system with one degree of freedom with constant parameters, where there is a single resonance at the natural frequency. At the same time, there is no distortion on the level graphic chart Fig. 1.

Fig. 1The amplitude-frequency characteristic with σf12=0 and σf32=0: A – amplitude, γ and γ1 – frequency of external and parametric action

With increase in variance of the parametric influence on the part of stiffness $σ_{f 3}^{2}$ , in the area of the main parametric resonance $γ_{1} =$ 2,0 the distortion of the amplitude-frequency characteristic is observed Figs. 2-4, which changes significantly the character of the dynamic processes in the system. Also there occur additional resonant peaks.

Fig. 2The amplitude-frequency characteristic with σf12= 0 and σf32= 0.04 (A – amplitude, γ and γ1 – frequency of external and parametric action)

Fig. 3The amplitude-frequency characteristic with σf12= 0 and σf32= 0.16 (A – amplitude, γ and γ1 – frequency of external and parametric action)

Very interesting is the case when the variance of the parametric effects, associated with rigidity, $σ_{f 3}^{2} =$ 1.0. Here there are two resonances, the most significant of which is observed at low frequencies Fig. 4. A further increase in this variance again changes the picture of the dynamic processes occurring in the system. Next, we consider the influence of the inertial parametric effect on the character of amplitude-frequency characteristics Figs. 5-8.

Fig. 4The amplitude-frequency characteristic with σf12= 0 and σf32= 1.0 (A – amplitude, γ and γ1 – frequency of external and parametric action)

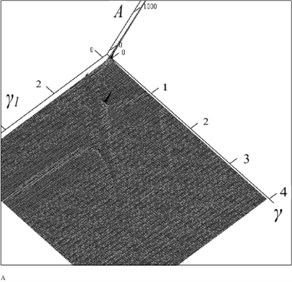
Fig. 5The amplitude-frequency characteristic with σf12= 0 and σf32= 1.44 (A – amplitude, γ and γ1 – frequency of external and parametric action)

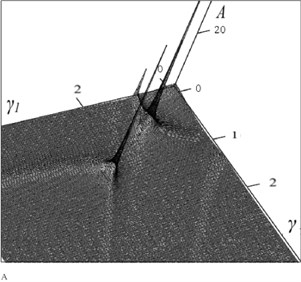
Fig. 6The amplitude-frequency characteristic with σf12= 0.04 and σf32= 0.04 (A – amplitude, γ and γ1 – frequency of external and parametric action)

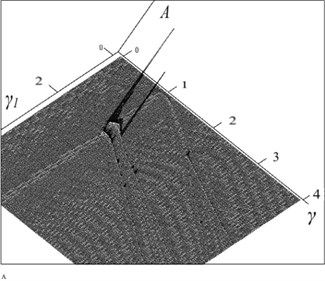
Fig. 7The amplitude-frequency characteristic with σf12= 0.04 and σf32= 0.16 (A – amplitude, γ and γ1 – frequency of external and parametric action)

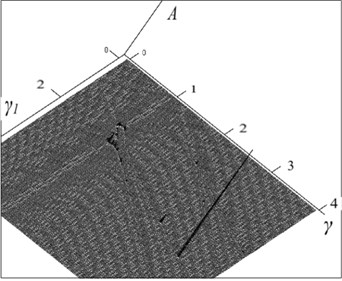
Fig. 8The amplitude-frequency characteristic with σf12= 0.04 and σf32= 1.0 (A – amplitude, γ and γ1 – frequency of external and parametric action)

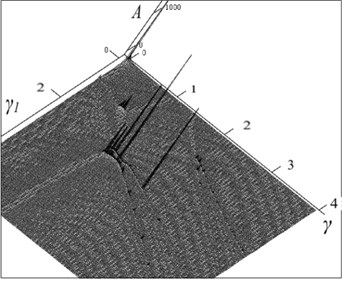
In this case, there is a qualitative change in the behavior of the system under external periodic effects. At low values of the inertial effect variance $σ_{f 1}^{2} =$ 0.04 on the amplitude-frequency characteristic there occur a group of resonant peaks. The most significant peaks are observed in the area of the main parametric resonance ( $γ_{1} =$ 2,0; $j =$ 100). With increase in this variance, the resonance peaks begin to shift from the resonant fields of parametric and forced oscillations. On the level graph charts these peaks are represented by dots. The shift of these resonances is connected, apparently, with the presence of other parametric resonances besides the main one. Each of them can only appear when there is a certain combination of frequencies of the external and parametric effects, because the system becomes sensitive to even a slight change in its parameters.

4. Conclusions

In [7] the results of the study of forced oscillations in mechanical systems were presented in the form of amplitude-frequency characteristics with fixed values of frequency and variance of parametric random effects. In order to have a complete understanding of the dynamic processes in these systems, within the framework of the method adopted in this work, it is necessary to analyze a significant number of amplitude-frequency characteristics. The results obtained show that the increase in the variance of the parametric effect, associated with the stiffness of the system, leads to an increase in the number of resonant peaks, because any slight change in the parameters of the effect can change their appearance significantly.

References

Bolotin V. V. Sluchainye Kolebaniya Uprugikh Sistem (Random Oscillations of Elastic Systems). Nauka, Moscow, 1979, (in Russian).

Search CrossRef
Klyatskin V. I. Stokhasticheskie Uravneniya i Volny v Sluchaino-Neodnorodnykh Sredakh (Stochastic Equations and Waves in Randomly Inhomogeneous Mediums). Nauka, Moscow, 1980, (in Russian).

Search CrossRef
Dimentberg M. F. Nelineinye Stokhasticheskie Zadachi Mekhanicheskikh Kolebanii (Nonlinear Stochastic Problems of Mechanical Oscillations). Nauka, Moscow, 1980, (in Russian).

Search CrossRef
Kolovsky M. Z. Dynamics of Machines. Mashinostroenie, 1989, (in Russian).

Search CrossRef
Babitskyv I., Krupenin V. L. Vibration of Strongly Nonlinear Discontinuous Systems. Springer-Verlag, Berlin, Heidelberg, New York, 2001.

Search CrossRef
Krupenin V. L. Investigation of one-dimensional and multidimensional vibroimpact processes during random broadband excitation. Journal of Machinery Manufacture and Reliability, Vol. 39, Issue 6, 2010, p. 530-538.

Search CrossRef
Roev B. A. Forced and Parametric Oscillations. Technical Application. LAP LAMBERT Academic Publishing, 2013.

Search CrossRef
Vinokur A. I., Roev B. A., Yakovlev R. V. Stability of reversed pendulum under random fluctuation of its fulcrum. Proceedings of the Institutions of Higher Education, Issues of the Graphic Arts and Publishing, Vol. 1, 2015, p. 14-19, (in Russian).

Search CrossRef

About this article

Received

07 September 2016

Accepted

12 September 2016

Published

07 October 2016

SUBJECTS

Mechanical vibrations and applications

Keywords

variance

carrier frequency

parametric effect

resonance

random process

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.