Slow oscillations in systems with inertial vibration exciters

1. Introduction

Inertial vibration exciters are used to drive a wide variety of vibration machines. Most of these machines operate in resonance mode. The problem of their passage through the resonance zone is quite important for vibration engineering. It has been well studied already. A review of the works in this field is given, for example, in the books [1, 2]. In particular, these studies draw our attention to the fact of existence of fast, slow and semi-slow motions in the region of the Sommerfeld effect. The existence of semi-slow rotor motions nearby the resonance zone of the carrier system was mentioned in [3-6]. It is important that semi-slow oscillations are used to facilitate the passage of vibration machines though the resonance zones.

In [3], a quantitative analysis of semi-slow oscillations of an unbalanced rotor is performed; an expression for the frequency of such oscillations is obtained. Attention is drawn to the fact that the equation of semi-slow oscillations can be used to improve the start-up control systems for super resonance vibration machines. Practical examples of the use of semi-slow motions to facilitate the passage through the resonance zone are considered in [7-9].

This paper is devoted to the extension of the results obtained in [3]. Using the direct motion separation method it is shown that the general solution for the fast motion equation describes a transition process towards ascertainment of a stationary motion mode of an unbalanced rotor in the resonance zone of vibration machine, as well as that semi-slow oscillations of the rotor speed are seen as transition process in the region of the Sommerfeld effect.

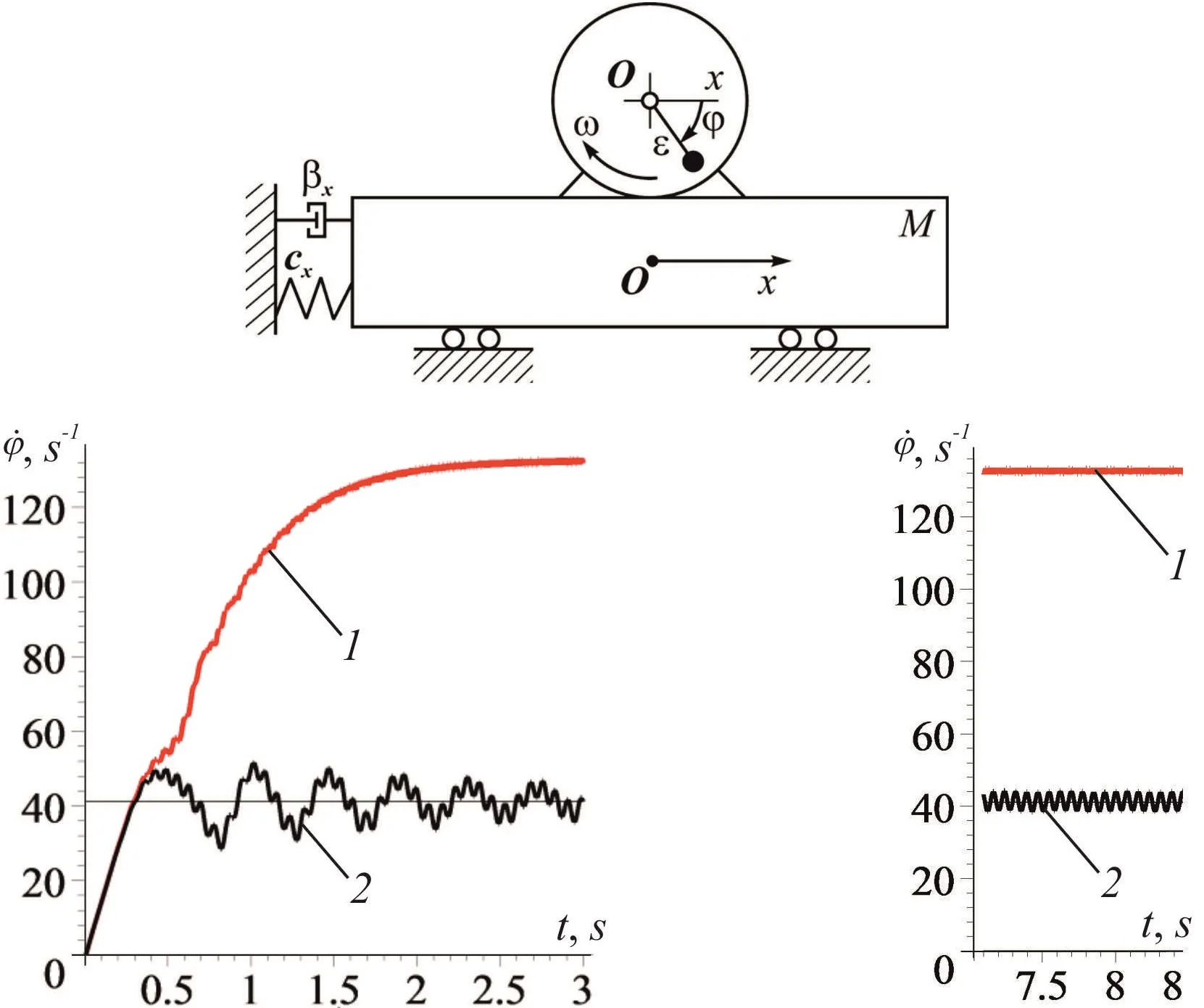
2. Dynamic model and system motion equations

The dynamic model of the vibration machine is adopted in the form of a bearing body connected with a fixed base by linear elastic and damping elements; with an unbalanced vibration exciter (unbalanced rotor) driven by an asynchronous electric motor (Fig. 1) placed on. The bearing body can move only in a strictly fixed direction $Ox$. The equations of system motions can be represented as:

where $\phi$ – rotor angle; $x$ – relocation of bearing body; $I$ – rotor moment of inertia; $m$, $\epsilon$ – rotor mass and its eccentricity; $c_x$ – coefficient of elastic element axial stiffness; ${\beta }_x$ – coefficient of elastic element viscous friction; $L\left(\dot{\phi }\right)$ – electric motor torque (its static characteristic); $R\left(\dot{\phi }\right)$– moment of resistance to rotation; $g$ – gravity acceleration.

Fig. 1Dynamic model of vibration machine

3. Semi-slow speed oscillations of unbalanced rotor

To study the motion of the rotor during its passage though the resonance zone we use the method of direct separation of motions [1, 2]. Looking for solutions to system Eqs. (1), (2) in the form of $\dot{\phi }=\omega \left(t\right)+\dot{\psi }\left(t,\mathrm{}\omega t\right)$, $x=x\left(t,\mathrm{}\omega t\right)$, we consider $\omega \left(t\right)$ – as slow, and $\dot{\psi }$ and $x$ – as fast $2\pi$ – periodic in $\tau =\omega t$ functions, while their average value over the period on $\tau$ equals to zero; we also accept that $\dot{\psi }\ll \omega$. We are determining the coordinate $\phi$ in the following way: $\phi =\omega \left(t\right)\mathrm{}t+\alpha \left(t\right)+\psi \left(t,\mathrm{}\omega t\right)$, where $\alpha \left(t\right)$ is some function $t$, which we consider as slow one; we will disregard it in the future.

Note that the “sticking” mode of the rotor speed during slow passage of the vibration machine through the resonance zone is of particular interest because its the most loaded mode of its operation.

Following this method, we get the equations of slow and fast rotor motions in the form obtained in [2]:

where $V\left(\omega \right)=m\epsilon ⟨\ddot{x}\mathrm{s}\mathrm{i}\mathrm{n}\phi +g\mathrm{c}\mathrm{o}\mathrm{s}\phi ⟩$ – vibration moment; $k$ – total damping coefficient; $\mu \mathrm{\Psi }(\ddot{x},\phi )=m\epsilon (\ddot{x}\mathrm{s}\mathrm{i}\mathrm{n}\phi +g\mathrm{c}\mathrm{o}\mathrm{s}\phi -⟨\ddot{x}\mathrm{s}\mathrm{i}\mathrm{n}\phi +g\mathrm{c}\mathrm{o}\mathrm{s}\phi ⟩)$; $\mu$ – small parameter.

Here and down the text, angle brackets indicate the averaging over a period $T=2\pi$ by quick time $\tau$. Moments $L\left(\dot{\phi }\right)$, $R\left(\dot{\phi }\right)$ linearized nearby “sticking” frequency $\dot{\phi }=\omega$ ($\omega \le p_x$), according to the formulas $L\left(\dot{\phi }\right)=L\left(\omega \right)-k_1\dot{\psi }$, $R\left(\dot{\phi }\right)=R\left(\omega \right)+k_2\dot{\psi }$, when $k_1+k_2=k$, $k_1$, $k_2$ – electrical and mechanical damping factors [2]; $p_x=\sqrt{c_x/M}$.

In [2] in the initial approximation, $\psi ={\psi }^{\left(0\right)}=0$, ${\phi }^{\left(0\right)}=\omega t$, $x^{\left(0\right)}=A_x^{\left(0\right)}\mathrm{c}\mathrm{o}\mathrm{s}(\omega t-{\gamma }_x)$, was obtained the expression for the vibration moment:

where:

In Eq. (5) value $A_x$ represents the amplitude of the stationary forced oscillations described by the equation $M\ddot{x}+{\beta }_x\dot{x}+c_{x}x=m\epsilon {\omega }^2\mathrm{c}\mathrm{o}\mathrm{s}\omega t+{\mu }^{2}X$.

Expression for vibration moment Eq. (5) is the following:

where $A_{st}=m\epsilon /M$ – the amplitude of steady-state induced resonant oscillations; $k_{dyn}=\frac{{\lambda }_x^2}{\sqrt{{\left(1-{\lambda }_x^2\right)}^2+4h_x^2{\lambda }_x^2}}$ – dynamic coefficient; ${\lambda }_x=\omega /p_x$; $h_x=b_x/p_x$.

According to Eq. (6), the magnitude of the vibration moment is proportional to the square of the dynamic coefficient, i.e. its frequency dependence is of a substantially resonant character. Thus, when the rotor passes slowly through the resonance zone, there is a rapid increase in the inhibitory vibration moment, which leads to the frequency “sticking”. To analyze the transition process towards the steady rotor motion in the region of the Sommerfeld effect, let’s examine the equation of fast motions Eq. (4). We represent Eqs. (4) in the form obtained in [3] while studying the semi-slow oscillations of the rotor ($\phi =\omega t+\psi$):

Note that the same as in [3], we do not take into consideration the effect of the gravity moment on the ongoing dynamic processes.

By linearizing the right side Eq. (7) on $\psi$ taking into account the solution of the Eq. (2) as $x^{\left(0\right)}$, we give the equation of fast motions in the form:

where:

Note that the estimates of the terms of the fast motions equations made in [3, 10] were taken into account above.

As we can see, the equation of fast motions takes the form of the equation of small forced oscillations; the coefficient $c_{\psi }$ can be called the conditional stiffness coefficient. In case of a slow passage through the resonance zone, the coefficient $c_{\psi }$ begins to increase significantly; when $\omega =p_x$ – it turns into zero. If the frequency exceeds the critical value $\omega =p_x$, the coefficient $c_{\psi }$ takes a negative value, and, accordingly, the stationary mode becomes unstable. Therefore, the term $c_{\psi }\psi$ is so called a restoring moment; when $\omega <p_x$ it “ensures” the stability of the stationary regime in the region of the Sommerfeld effect.

In Eq. (8), the value $p_{\psi }$ represents the natural frequency of so-called semi-slow oscillations of the unbalanced rotor. A detailed analysis of the expression for the frequency is given in [3]; it is shown that for the validity of the equation of semi-slow oscillations it is necessary that $\omega /p_{\psi }>3$, as a rule, this condition is satisfied for vibration machines under study.

To study the transition regime towards steady motion in the region of the Sommerfeld effect, we have to find the general solution of the fast motion Eq. (9). For clarity, we will disregard the influence of resistance forces. At the same time, we take into account that: the effect occurs with a rapid increase in the vibration moment $V\left(\omega \right)$, which action can be evaluated by impetus ($2\omega \gg p_{\psi }$); inhibitory effect of vibration moment occurs during the half of its oscillations period; prior to the occurrence of the effect the rotor speed oscillations are relatively small. Consequently, the initial conditions are presented as ${\psi }_0=0$, ${\dot{\psi }}_0=-V_{\mathrm{m}\mathrm{a}\mathrm{x}}/I\omega$. Then, the expression describing the oscillations of the rotor frequency during the establishment of a stationary mode will be presented as follows:

where ${\mathrm{Ф}}_1=-\frac{V_{\mathrm{m}\mathrm{a}\mathrm{x}}}{I\omega }-\frac{2\omega V_{\mathrm{m}\mathrm{a}\mathrm{x}}}{I(4{\omega }^2-p_{\psi }^2)}$, ${\mathrm{Ф}}_2=\frac{2\omega V_{\mathrm{m}\mathrm{a}\mathrm{x}}}{I(4{\omega }^2-p_{\psi }^2)}$.

Let’s analyze the resulting solution. In this case, we have to recall the assumption adopted above on disregarding the friction forces, they only dampen free vibrations in the case $p_{\psi }\ll \omega$. Therefore, when a stationary mode of rotor rotation is established, a transient process takes place, which can be described as a damping biharmonic oscillation of the rotor speed with a fundamental frequency equal to the frequency $p_{\psi }$, i.e. non-stationary process looks like a relatively slow oscillations. It is not difficult to establish that the initial amplitudes of these oscillations are large enough, they are at least a third as much as the amplitudes of the stationary regime that is being established subsequently. Of course, semi-slow oscillations are dampening over time and turn into purely forced monoharmonic oscillations.

4. Results of computer simulation

During the simulation, the following parameter values were set: $M=$ 40 kg; $m=$ 3 kg; $\epsilon =\mathrm{}$0,03 m; $I=\mathrm{}$0,006 kg⋅m²; $c_x=$ 7,5⋅10⁴ N/m; ${\beta }_x=$ 135 kg/s; electric motor – asynchronous, with a frequency $n_s=$ 1500 rtm, power $P=$ 0,6 kW [11].

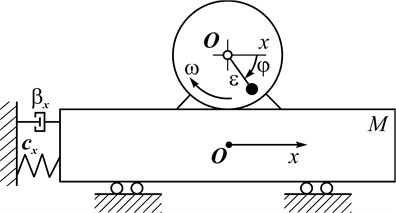
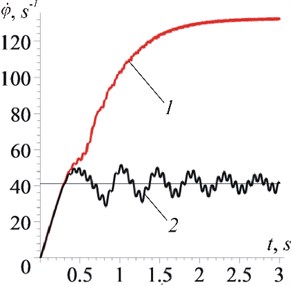
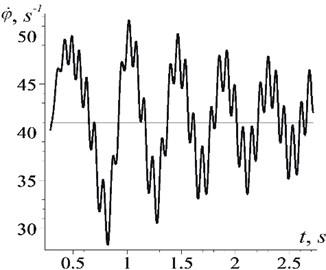
Fig. 2Change of rotor speed spinning in time: a) from the moment of the engine start-up; b) in the steady regime: 1 – passage through the resonance zone; 2 – speed “sticking”

a)

b)

As it can be seen from the graphs Fig. 2(a), Fig. 3(a), when the rotor speed is “sticking”, biharmonic oscillations are excited, which are the result of superimposement of damping oscillations with a relatively low frequency (13,8 s^-1), approximately equal to the frequency $p_{\psi }$, on fast oscillations (83,7 s^-1), frequency of which is close to the doubled frequency of the rotor speed “sticking” ($2\omega \approx$ 83 s^-1; $\omega \approx p_x=$ 43,3 s^-1) In this case, the initial amplitudes of such oscillations are quite large (the maximum reaches 11,8 s^-1, but subsequently, in the stationary mode they decrease to 3,3 s^-1), and the dampening of semi-slow oscillations is relatively slow (up to 5 s).

The graphs in Fig. 2 convincingly indicate that semi-slow oscillations are seen as an unsteady process in the region of the Sommerfeld effect.

The simulation results are in good agreement with the calculation results according to the formulas obtained: $p_{\psi }\approx$ 13,3 s^-1; ${\mathrm{Ф}}_1\approx$ 8,5 s^-1, ${\mathrm{Ф}}_2\approx$ 2,9 s^-1 (the frequency of “sticking” is accepted according to Fig. 2 and is equal to $\omega \approx$ 41,4 s^-1).

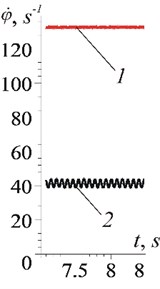
In support of the foregoing, a graph (Fig. 3(b)) of the rotor frequency oscillations during the speed “sticking” is presented, a graph was obtained as a result of a numerical solution of the fast motion Eq. (9). Comparing this graph with the numerical solution of the initial system of Eqs. (1), (2), we can conclude that the results are well comparable and describe the same dynamic process.

Fig. 3Change of rotor speed spinning in stationary regime obtained by numerical solution: a) the initial system of motion Eqs. (1), (2); b) equations of fast motions Eq. (9)

a)

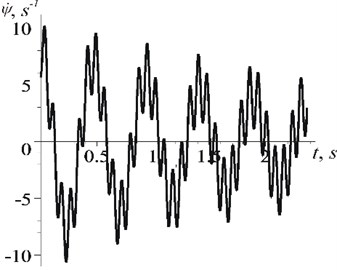
b)

5. Results and discussion

Thus, when a speed of the unbalanced rotor stucks in the resonance zone, its relatively slow (compared to the frequency $\omega$) damping oscillations are excited. Taking into account the quantitative estimates of parameters of motions (frequencies) taking place in the system, such oscillations are often called semi-slow.

The described regularity of the system motion is also represented as the presence of the “inner pendulum” and its semi-slow oscillations in the region of the Sommerfeld effect. The natural oscillation frequency of the “inner pendulum” is also called the “Blechman frequency” [8]. Using this approach, it can be easily found with sufficient accuracy for practical use.

The maximum amplitudes of the arising semi-slow oscillations of the rotor speed are quite large, and their dampening happens slowly, thus it can be of a significant danger for vibration machines [11].

Following the approach used, it is easy to show that the action of the gravity moment on the rotor does not directly have a significant effect on the dynamic processes under study.

For the case when the oscillatory part of the system has several degrees of freedom, the equation of semi-slow oscillations retains its form. Only the expression for the frequency of semi-slow oscillations is changing, the methodology used for determining is the same.

6. Conclusions

Semi-slow speed oscillations of the unbalanced rotor observed during the vibration machine passage through the resonance zone are seen as a transition process towards the steady rotor motion in the region of the Sommerfeld effect.

Semi-slow speed oscillations can cause significant drive vibrations, that must be taken into account when designing this type of vibration machines.

The conducted research will contribute to the selection of parameters for the algorithms for controlling the passage of vibration machines with inertial vibration exciters through the resonance zone.