Engineering model of the vibrational transportation process

1. Introduction

The most common existing model of the vibrational transportation process for solids and granular materials treats the material transported as a single body (a material point) moving without the air resistance. The interaction of the body with the vibrating surface is taken into account in the law of Coulomb (dry) friction and the stereomechanic impact theory [1-9]. For brevity, this will be referred to as the basic model.

In a large number of vibrating machines, the particle motion regime implemented implies that the particles are systematically separated from the vibrating surface. Moreover, in the most common ranges of parameter variations, the basic model predicts the possibility of many different motion regimes, with their minor domains of existence and stability adjoining or overlapping in the parameter space. In the phase space, these regimes correspond to minor domains of attraction [1-10]. Under the above conditions, it apparently makes no sense to calculate the vibrational transportation velocities for each regime, especially since this does not correspond to the parameter setting accuracy. In such cases, it seems more appropriate to consider a simpler (“crude”) process model. In this model, the process is represented as a series of particle throws at a certain angle to the horizon, where the longitudinal displacement of the material is deemed to be caused by such throws. As a result, using certain additional assumptions, simple formulas may be obtained for estimating the vibrational transportation velocity, suitable in a wide working range of parameter variations. The calculation results for the formulas proposed are in good agreement with the experiments, both available in the literature and obtained in this work.

In connection with the study, the general topic of rational modeling of similar systems with complex behavior (multiplicity of regimes, multistability) is discussed [11-14].

2. On the basic model of vibrational transportation

The “basic” model mentioned above leads to the consideration of a substantially nonlinear or, more precisely, “piecewise linear” system with a variable structure. In accordance with the model, the material point may be separated from the vibrating surface, may rest on the surface, or may be sliding in one direction or the other. The general case considered implies motion along a plane performing rectilinear translational harmonic oscillations with the amplitude of $A$ and frequency of $\omega$ at a certain angle of $\beta$ to the plane; and the plane may be tilted to the horizon at an angle of $\alpha$ (see Fig. 1).

Fig. 1Oscillations of machine working surface

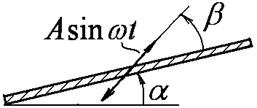
The longitudinal and transverse projections of the oscillation velocity for the points of the plane are determined by the following formulas:

If the transverse overload parameter:

is less than 1, then the particles are moving without detaching from the plane; and if the parameter is over 1, then the particles periodically separate from the surface. There are only several types of separation-free steady motion (regimes) [1-3]. For the detaching motion, however, such regimes are numerous (see, in particular, [1-10]), especially with the parameter values of $\text{2.0}<w_v<\text{6.5}$ (see, for example, [3], p. 23, Fig. 6) that are characteristic of a large number of machines of this type. The conditions here are as described in the introduction (multiplicity of regimes, multistability). Obtaining vibrational transportation velocity formulas for each of the regimes seems pointless. It, therefore, seems adequate to apply a “crude” model of the process, avoiding the above-mentioned complexity. Such a model may only be valid in the above range of the most commonly used parameter values of $w_v$ and only with respect to the vibrational transportation velocity, being the integral characteristic of motion. In addition, there is reason to believe that the vibrational transportation velocity value is a smooth monotonous function of the system parameters.

3. Process engineering model, vibrational transportation velocity

The model proposed is extremely simple. It is assumed that the vibrational transportation process consists of a sequence of particle throws at an angle to the horizon and uses certain elements of the basic model.

Let us first consider the case of a horizontal plane of $\alpha =0$. It is also assumed that the recovery coefficient is $R=0$, that is, the impact is absolutely inelastic. We believe that the throw of a particle weighing $m$ occurs at an angle of $\beta$ to the horizon, starting at the point in time of $t_0$, when, similarly to the basic model, the normal reaction $N=mg-mA{\omega }^2\mathrm{s}\mathrm{i}\mathrm{n}\beta \mathrm{s}\mathrm{i}\mathrm{n}\omega t$ acting on the particle vanishes. In this case, the initial velocity is equal to the velocity of the plane at the moment of separation $t=t_0$. At this point, the separation phase ${\delta }_0$ is described by:

and the following is valid for the projections of the initial velocity:

Let us first consider a particle flight under the assumption that the plane is motionless (we will find out below that this assumption is true for the regimes of interest). The flight duration $t_{\mathrm{*}}$ is determined using the elementary equality of $A\omega \mathrm{s}\mathrm{i}\mathrm{n}\beta =\frac{1}{2}g{t}_{\mathrm{*}}$, and the corresponding phase angle is:

Let us assume that, in the regimes considered, the particle flight occurs only once per period of motion velocity variation $T_p$, and the particle longitudinal displacement occurs only during the flight. Then the average particle velocity, i.e. the vibrational transportation velocity, will be:

Let us use $\phi$ and ${\delta }_0$ to denote the phase angles of the end and start of the flight; then ${\phi }_{\mathrm{*}}=\phi -{\delta }_0$. According to Eq. (5), at $w_v=\pi p$, the particle flight continues for exactly $p$ oscillation periods of the plane $T_0=2\pi /\omega$ and the particle contacts with the plane only when $\phi ={\delta }_0+2\pi p$, that is, there are continuous tossing regimes. In such regimes, the plane occupies the same position at the moments of collision, and the longitudinal displacement of the particle occurs only during the flight. In other words, for such conditions, Eq. (6) is correct in the sense of the basic model. Let us also note that, in the range of values close to $w_v=\pi p$, the regimes under consideration are also observed in the basic model and the values of ${\phi }_{\mathrm{*}}=2w_v$, according to Eq. (5), are close to those determined for the basic model by solving the transcendental equation for $\phi$ (see [1], p. 157, Eq. (11.4)). Therefore, when $w_v=\pi p$, Eq. (6) yields $v_m=A\omega \mathrm{c}\mathrm{o}\mathrm{s}\beta$. It seems logical to assume that this expression will also be approximately true for the intermediate values of $w_v>\pi$.

When using this approximation, we assume that the physical value of vibrational transportation velocity monotonically depends on the parameters of $A\omega$ and $w_v$. As a result, we obtain the following formulas:

It is somewhat more difficult to obtain the corresponding formulas for $\alpha \ne 0$ and $R\ne 0$. Let us take these without the conclusion based on the formula from the [3] (see Eq. (31), p. 28):

where $\left|\alpha \right|<\rho =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}f$; $f$ and $\rho$ are the coefficient and angle of sliding friction, respectively; and $\lambda$ is the coefficient of instant friction.

4. Comparison with experimental data

The experimental determination of vibrational transportation velocities of individual bodies and granular materials is covered in a number of works, reviewed in the Handbook [3]. Among the recent works on the subject, let us particularly note [15, 16]. There are also data covering material displacement velocities on vibrating screens [17] (see also [15]). The calculation results for Eq. (7-10) demonstrate good agreement with the data listed. The coincidence of Eq. (10) with the empirical formula of L.P. Levin [18] is notable, presented in our work in the form of $v_m=\frac{2}{\pi }A\omega \mathrm{c}\mathrm{o}\mathrm{s}\beta \approx 0.64A\omega \mathrm{c}\mathrm{o}\mathrm{s}\beta \text{.}$ Namely, when $\alpha =\text{0}$ and $R=\text{0.2,}$ Eq. (10) yields $v_m=0.67A\omega \mathrm{c}\mathrm{o}\mathrm{s}\beta$. The study performed actually translates this empirical formula into the status of a theoretically substantiated formula.

Fig. 2Dependence of the dimensionless transportation velocity on the transverse overload wv (1, 2, 3 are the calculated dependencies: 1 is R=0; 2 is R=0.2; 3 is R=0.25 (Eq. (9), (10)); 4 is the empirical dependence [18]; the experimental values are as follows: ● – pieces of crushed stone, ▲ – pieces of rubber, ■ – a copper cylinder, O – granular material)

In addition, special experiments were carried out in this work for the vibrational transportation of single-piece materials (20-40 mm crushed stone pieces, rubber pieces, a copper cylinder) and a fine crushed stone bed (fraction of 3–7 mm) with the thickness of approx. 10 mm. In the experiments performed using the vibration stand designed by Mekhanobr [19], the oscillation amplitude of the tray $A$ varied between 0.38 to 4.4 mm, with the frequency $\omega$ of 37.7 to 264 1/s (6–42 Hz). The tray was mounted horizontally, with the vibration angle $\beta$ of 45°. The experimental results are presented by points in Fig. 2; solid lines show the results of calculations using the formulas proposed. The figure demonstrates good agreement between the theoretical and experimental results at the recovery coefficients of $R=$ 0.20-0.25. The coefficient values were established experimentally.

The experiments have confirmed the smooth monotonic nature of the dependence between the velocity $v_m$ and the overload factor $w_v$, including in the ranges where various particle motion regimes are present according to the basic model. The linear nature of the dependence between $v_m$ and $w_v$ has also been confirmed at a constant value of $A\omega$ in the range of $w_v<\pi$, as well as the practical independence of $v_m$ from $w_v$ at $w_v>\pi$.

5. On modeling dynamic systems with complex behavior

The study touches on the general problem of rational modeling of a dynamic system. Similarly to the problem considered, let us assume complex behavior of the system modeled: in a certain domain of the parameter space, there are a large number of steady motion regimes; their minor domains of existence and stability are closely adjacent or overlapping; and, in the phase space, these regimes correspond to certain minor domains of attraction (multiplicity of regimes, multistability). At the same time, the parameters setting accuracy does not correspond to the sizes of the domains indicated. Let us find a certain integral characteristic of the regimes, similar to the average motion velocity considered above or energy consumption. Note that the situation described is characteristic of piecewise smooth systems and discontinuous systems [20] and is also observed for a number of “smooth” systems, for example, in the problem of the behavior of a pendulum with a vibrating suspension axis [4, 21-23]. It seems that, in such a situation, it would be advisable, for example, to consider a more “crude” model, as it was done above. Another way is to use approximation methods, in particular, those related to the averaging idea [4, 20] (which, however, is often the same) or a probabilistic description.

Let us also note that the idea of moving from a model with Coulomb friction to a “smooth” model was successfully used in [24] for numerical studies.

6. Conclusions

Simple model representations are used in the work to obtain formulas for estimating the vibrational transportation velocity in intensive tossing regimes that are characteristic of a wide class of vibrational transportation and process machines. A simple formula has also been obtained for the significant process value of the material dimensionless flight time (flight phase). It turned out to be double the value of the transverse overload factor. The calculation results for the formulas proposed are in good agreement with the experimental data. The issues of modeling similar systems with complex behavior have been discussed.