On the dynamics of vibrational capture of rotation of an unbalanced rotor

1. Introduction

Vibrational maintenance of rotation of an unbalanced rotor under the action of axis vibrations is an important nonlinear effect underlying the principle of operation of a number of machines. The effect is successfully used in cone inertial crushers and ore grinders, vibrating screens, mills and feeders, as well as in vibration motion converters.

A large number of works have been devoted to the study of the effect. The presentation and generalization of the main research results are given in monographs [1, 2]. Practically important issues related to the determination of the field of attraction of certain stationary modes of rotation of the rotor under the action of axis vibration were considered in [3-5]. Among the recent works devoted to the practical use of the effect, we can note the articles [6-8].

In the monograph [1], attention is drawn to the fact that a relatively simple description of the effect of vibrational maintenance of rotation of an unbalanced rotor is obtained on the basis of the approach of vibrational mechanics and the method of direct separation of movements. Note that in the monograph [9] this method considers the main and some multiple modes of stationary rotation of an unbalanced rotor under the action of vibration.

The proposed work is devoted to the further development of the studies of the effect of vibrational maintenance of rotation of an unbalanced rotor, given in [1, 2]. Using the method of direct separation of movements, an engineering interpretation of the phenomenon of vibrational capture of rotation of an unbalanced rotor is obtained. For the case when the resistance to rotation is mainly due to friction in the bearings, a simple condition for the existence of a stationary mode of motion is obtained.

2. Description of the system and the equation of motion

Let us consider an unbalanced rotor (unbalanced vibration exciter), the suspension axis of which performs vertical harmonic oscillations excited by an ideal energy source according to the law $y=A\mathrm{c}\mathrm{o}\mathrm{s}\omega t$ (Fig. 1). It is assumed that the axis of the rotor is horizontal, and the direction of oscillation is perpendicular to the axis. Note that the more general case of axis oscillations in two mutually perpendicular directions studied in [1, 2] does not fundamentally differ from the one under consideration, but requires more cumbersome calculations.

The equation of motion of an unbalanced rotor with a vibrating axis has the form:

where $I$ – the moment of inertia of the rotor; $\phi$– the angle of rotation of the rotor; $L\left(\dot{\phi }\right)$– the torque of the electric motor;$R\left(\dot{\phi }\right)$ – the moment of the forces of resistance to rotation of the rotor; $m,\epsilon$ – the mass and eccentricity of the rotor; $A$, $\omega$ – the amplitude and frequency of oscillations of the rotor axis; $g$ – acceleration of gravity.

Fig. 1An unbalanced rotor whose axis performs harmonic oscillations

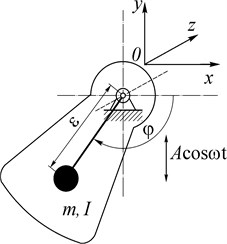
We believe that the moment $R\left(\dot{\phi }\right)$ can take into account not only the resistance in the rotor bearings, but also the payload; the rotor is driven by an asynchronous electric motor. Taking into account that stationary modes of motion are studied below, we will take into account the moment of the engine using its static characteristics.

3. Equation of slow movements of an unbalanced rotor

Let us study the basic mode of stationary rotation of the rotor, i.e. its rotation with an average angular velocity ${\dot{\phi }}_m$ equal to (close to) the frequency of axis oscillations. Limiting the motion of the rotor to a little different from the uniform one, we present Eq. (1) in the form [1]:

where $k=k_1+k_2$ – total damping coefficient; $\mu >0$ – small parameter; $Ф\left(\phi ,\omega t\right)=L\left(\omega \right)-R\left(\omega \right)-m\epsilon ({\omega }^{2}A\mathrm{c}\mathrm{o}\mathrm{s}\phi \mathrm{c}\mathrm{o}\mathrm{s}\omega t-g\mathrm{c}\mathrm{o}\mathrm{s}\phi )$.

When Eq. (2) is obtained, the moments are linearized $L\left(\dot{\phi }\right)$, $R\left(\dot{\phi }\right)$ near the frequency $\dot{\phi }=\omega$, and $k_1=-(dL\left(\dot{\phi }\right)/d\dot{\phi }{)}_{\dot{\phi }=\omega }>0$, $k_2=(dR\left(\dot{\phi }\right)/d\dot{\phi }{)}_{\dot{\phi }=\omega }>0$ [1].

Using the method of direct separation of movements, we will study the rotation of the rotor of the form $\phi =\omega t+\alpha \left(t\right)+\psi \left(t,\omega t\right)$. At the same time, we consider $\alpha \left(t\right)$ to be slow, and $\psi \left(t,\omega t\right)$ to be small fast $2\pi$ – periodic by $\tau =\omega t$ function, whose average value for the period is zero $⟨\psi \left(t,\omega t\right)⟩=0$. The angle brackets $⟨\dots ⟩$ indicate the averaging of the expression contained in them over a period $2\pi /\omega$ of fast time $\tau$.

Following the traditional procedure of the method used, we write down the equations of slow and fast rotor movements in the form [1]:

where $V\left(\omega \right)=-m\epsilon ⟨{\omega }^{2}A\mathrm{c}\mathrm{o}\mathrm{s}\phi \mathrm{c}\mathrm{o}\mathrm{s}\omega t-g\mathrm{c}\mathrm{o}\mathrm{s}\phi ⟩$.

In Eq. (3), the expression $V\left(\omega \right)$ is the so-called vibrational moment [1] – the average value of the additional moment acting on the rotor due to axis vibrations. When using this method, it is possible to solve the equation of rapid motion approximately. Then, in the initial approximation we have $\psi ={\psi }^{\left(0\right)}=0$. With this solution in mind, we get $V\left(\omega \right)=-V_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{c}\mathrm{o}\mathrm{s}\alpha$, where $V_{\mathrm{m}\mathrm{a}\mathrm{x}}=m\epsilon {\omega }^{2}A/2$.

From Eq. (3) follows the well-known [1] condition $\left|L\left(\omega \right)-R\left(\omega \right)/V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right|\le 1$ for the existence of a stationary rotation of the rotor with a frequency $\omega$. In the case under consideration, when the angular velocities $\omega$ and $\dot{\phi }$ are not too different from each other, we represent this assumption in the form $\left|k({\omega }_0-\omega )/V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right|\le 1$, where ${\omega }_0$ – is the speed of steady rotation of the rotor in the absence of axis oscillations (the so-called partial velocity [1]). For cases, when the moment of resistance to rotation of the rotor is due to the friction in the bearings, this condition can be given a more practical form:

where $L\left({\omega }_n\right)$, ${\omega }_n$ – rated torque and rated speed of the electric motor; ${\omega }_c$ – synchronous motor speed; $F=m\epsilon {\omega }^2$ – amplitude of the driving force developed by an unbalanced rotor.

Note that when obtaining condition (5), the fact is taken into account that the effect of speed on the torque of an asynchronous electric motor is expressed very sharply, in contrast to the moment of the resistance forces in the bearings.

Condition Eq. (5) can be used for a rough assessment of possibility of the existence of a mode capturing the rotation of the rotor with the frequency of axis oscillation.

Obviously, when the rotor rotates at a speed ${\omega }_0$, close to the oscillation frequency $\omega$ condition Eq. (5) is necessarily fulfilled (it is assumed that the proximity of the intervals ${\omega }_0-\omega$ and ${\omega }_c-{\omega }_n$).

When condition Eq. (5) is met, the equation $L\left(\omega \right)-R\left(\omega \right)-V_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{c}\mathrm{o}\mathrm{s}\alpha =0$ admits two substantially different solutions: ${\alpha }_{\mathrm{1,2}}=\pm \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{L\left(\omega \right)-R\left(\omega \right)}{V_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)$. For the stability of the regime that meets the solutions ${\alpha }_{\mathrm{1,2}}$, it is necessary to fulfil the condition $\mathrm{s}\mathrm{i}\mathrm{n}\alpha <0$ [1]. Note that this condition is obtained by composing an equation in variations for Eq. (3) and solution ${\alpha }_{\mathrm{1,2}}$.

The general solution of Eq. (3) with respect to velocity $\dot{\alpha }$can be represented as ($t=0$, $\dot{\alpha }={\dot{\alpha }}_0$): $\dot{\alpha }=({\dot{\alpha }}_0-{\dot{\alpha }}_{st})e^{-kt/I}+{\dot{\alpha }}_{st}$, where ${\dot{\alpha }}_{st}=\left(L\right(\omega )-R(\omega )+V)/k$.

The Eq. (3) describes the slow process of establishing a stationary rotation mode of an unbalanced rotor with the frequency of axis oscillation. The duration of the transition process is determined by the value $T=I/k$ of the so-called time constant of the machine unit.

According to the expressions obtained, when the partial angular velocity ${\omega }_0$ coincides with the oscillation frequency of the axis $\omega$, the stationary solutions of Eq. (5) will be: ${\alpha }_{\mathrm{1,2}}=\pm \pi /2$; at the same time, the solution ${\alpha }_2=-\pi /2$ is stable. From the expression $V\left(\omega \right)=-V_{max}\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ follows that at the slightest deviation from ${\alpha }_2=-\pi /2$, a restoring moment appears. Hence, the effect of the vibrational moment $V\left(\omega \right)$ is reduced to the establishment and subsequent maintenance of a stable shift between the phases of oscillatory and rotational movements.

If the frequency of the resulting vibration $\omega$ is slightly different from the frequency ${\omega }_0$, the variable $\dot{\alpha }$ will asymptotically tend to the value ${\dot{\alpha }}_{st}=\pm \mathrm{\Delta }\omega$. In this case, the sustainable solution will be different from ${\alpha }_2=-\pi /2$. At the same time, when ${\omega }_0>\omega$, the phase shift $\alpha \left(t\right)$ between motions decreases, and when ${\omega }_0<\omega$ – increases (moreover, increases the more significantly the greater the difference in frequencies). Consequently, in these cases, vibration moment changes operator and, accordingly, its impact will be reduced to slowing down (case ${\omega }_0>\omega$, the vibration moment is negative) or pushing (${\omega }_0<\omega$, $V\left(\omega \right)$ – positive) the rotation of the rotor. As a result, the rotation of the rotor is ensured with a frequency equal to the frequency of the axis oscillations, moreover, with a certain phase shift. As we can see the vibration imposes its own rhythm of movement on the rotor.

The nature of the impact of vibration is determined, first of all, by the steady phase shift between rotational and oscillatory motion. Taking into account that modern means of controlling electric motors make it possible to control the phases of their rotation [10], it seems possible to control the impact of vibration.

The effect of vibration trapping of the rotation of an unbalanced rotor is clearly visible in Fig. 2, obtained by computer simulation. The parameters in Eq. (1) are as follows: $m=$ 30 kg; $\epsilon =$ 0.03 m; $I=$ 0.07 kg⋅m²; $A=$ 0.005 m; at the same time, a dynamic model of an asynchronous electric motor with $P=$ 1.5 kW and $n_c=$ 1500 rtm, given in [11, 12], was used. Note that in Fig. 2, at the moment of time $t=$ 1.1 s, the rotor axis begins to make vertical vibrations; after a short transient process, the rotor rotation frequency becomes equal to the vibration frequency $\omega$ ($\omega =$ 146 s^-1 or the second curve – $\omega =$136 s^-1, horizontal straight – ${\omega }_0\approx$ 141 s^-1); the dashed line shows the asymptotic tendency of the partial speed of the rotor ${\omega }_0$ to the value $\omega$; phase shift in case of vibration braking $\alpha \approx$ –1.53 rad$>{\alpha }_2$, while maintaining rotation – $\alpha \approx$ –1.64 rad $<{\alpha }_2$.

Thus, if before the occurrence of a stationary mode of motion, vibration both slows down and accelerates the rotation of the rotor according to some arbitrary law. After establishment of the stationary mode, its effect becomes single-valued: only braking or only rotational. This means that in the stationary mode of motion, an unbalanced rotor with a vibrating axis either gives off or takes away energy from the source of vibrations.

It is obvious that the manifestations of vibration increase with a large static moment of the rotor, as well as with high frequencies and amplitudes of vibrations of the rotor axis. Consequently, the described effects can occur with resonant phenomena in the carrier system of rotary mechanisms.

Fig. 2Changes in time: a) the rotation frequency of an unbalanced rotor; b) the phase shift between rotational and oscillatory movements: 1) ω= 146 s-1; 2) ω= 136 s-1

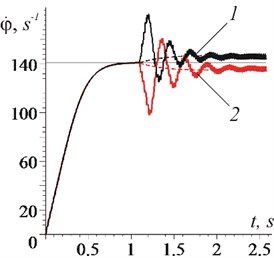
a)

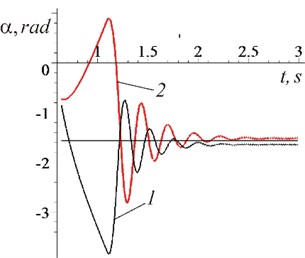
b)

Note that the results obtained also apply to the start-up and run-out modes. So during run-up of the rotor the vibration moment becomes moment becomes commensurate with the starting torque of the engine, and during the run-out – with the moment of resistance to rotation, the rotor speed may “get stuck” at the vibration frequency. This fact is confirmed by computer modelling.

As you can see, the vibration of the axis of an unbalanced rotor during start-up can lead to the Sommerfeld effect, and in stationary mode – to a change in the average rotational speed and to a significant increase of the amplitudes of its oscillations. Obviously, in the case of an arbitrary periodic vibration of the rotor axis, represented as a decomposition $y=\sum _{n=1}^{\infty }{A}_n\mathrm{c}\mathrm{o}\mathrm{s}(n\omega t+{\gamma }_n)$, it is also possible to rotate it with velocity ${\dot{\phi }}_m=n\omega$ equal to the frequency of the corresponding harmonic.

4. The equation of fast movements of an unbalanced rotor

Consider Eq. (4) of fast movements of an unbalanced rotor. With the help of the methodology used in [13, 14], Eq. (4) it is not difficult to present in the form:

where $b_{\psi }=k/2I$; $p_{\psi }^2=c_{\psi }/I$; $c_{\psi }=-V_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{s}\mathrm{i}\mathrm{n}\alpha$; ${Ф}_v=-V_{\mathrm{m}\mathrm{a}\mathrm{x}}/I$.

Note that the effect of the moment of gravity on the rotation of the rotor is not taken into account.

As we can see, Eq. (6) takes the form of an oscillatory type equation. The coefficient $c_{\psi }$ can be called the dynamic (vibration) coefficient of rigidity; in stable stationary modes it is positive. The value $p_{\psi }$ is the frequency of small free oscillations of an unbalanced rotor or, according to [1, 2], the frequency of free pendulum oscillations of the rotor near a stable stationary mode. It is easy to establish that when the condition $A<\epsilon$ is met, the frequency $p_{\psi }$ is significantly less than the frequency $\omega$ (in the given example $p_{\psi }\approx$ 25 s^-1). This means that when a stationary rotation mode is established, there will be a pronounced transient process with large initial amplitudes and a relatively slow main frequency.

Note that the equations of slow oscillations of an unbalanced rotor are used to select the parameters of control systems for the process of passing the resonance zone during the start-up of vibration machines with an unbalanced drive [1, 12].

The excitation of slow (semi-slow) oscillations of unbalanced rotors on a vibrating base when establishing stationary rotation modes can be considered a general pattern [2, 14, 15].

5. Conclusions

In the stationary rotation mode of an unbalanced rotor with the axis oscillation frequency, a well-defined stable phase shift between rotational and oscillatory movements is established. Each such phase shift corresponds to a certain operator and magnitude of the vibration moment acting on the rotor. Consequently, in the stationary mode of rotation of the rotor, the effect of vibration (estimated by the vibration moment) becomes quite definite: only braking or rotational; braking – when the vibration frequency of the rotor axis is less than the partial frequency of its rotation; rotational – when $\omega >{\omega }_0$.

During the vibrational capture of the rotation of an unbalanced rotor, relatively slow non-stationary oscillations of its speed with large initial amplitudes can be excited.

The results obtained can be used to improve the control systems of mechatronic vibration installations.