On extreme values in queues in series

1. Introduction

A brief review of the latest achievements in the theory of queues in series after the year of 2005 is provided in this paper. A good example of studying queues in series behavior and valuable insights in order to understand the behavior of manufacturing systems is provided by Wu and McGinnis, [3]. Generally speaking, there are many practical manufacturing systems that can be modeled as queues in series. For example, any mixed-model assembly process has the structure of queues in series [3]. A realistic case, corresponding to this model, can be found in publishing companies, printing shops, etc. [4].

A practical multi-server case is a lot more sophisticated than single-server queues in series [5], since each workstation may have multiple servers with different capabilities and each server may have a complicated configuration. Obviously, such technical combinations suffer different types of interruptions. Modelling the behaviour of such a technical configuration by analysis of all the details is a formidable task [5].

In this paper, functional limit theorems for extreme values of the main characteristics of queues in series are proved in heavy traffic (maximum of the total virtual waiting time of a customer, maximum of the virtual waiting time of a customer). Recent investigations [6] show that under conditions of heavy traffic the network does not always agree with the regulated Brownian motion diffusion limit for the standard network without special arrivals. However, if the traffic fed into the system is generated by independent or weakly dependent sources and the smallest relevant time scale is not too fine, the central limit theorem suggests that the input traffic is close to Gaussian [2].

The main tool used in this paper for the analysis of queues in series in heavy traffic is functional limit theorems for renewal and compound renewal processes (the proof can be found in Billingsley, [7]). The same heavy traffic fluid limits for multi-server models were investigated by Liu and Whitt, [8]. Renewal process approximation and network performance measures of the single-server system are investigated in detail by S. Yeong Lin et al. [9], and Mei and Winands [10], where new fundamental insights on heavy traffic are provided and revealed explicitly, especially how the expected delay at each of the queues depends on the system parameters, and on the interarrival time distributions at each of the queues.

In this paper, the natural setting for functional limit theorems is the weak convergence of probability measures on the function space $D\left[\mathrm{0,1}\right](\equiv D).$ Since an excellent treatment of this subject has been published by Billingsley [7], we shall only make a few remarks in regards to our terminology and notation. Stochastic processes characterizing a queueing system give rise to sequences of random functions in $D$, the space of all right-continuous functions on $\left[\mathrm{0,1}\right]$ having left limits and endowed with the Skorohod metric, $d$ [11]. In Billingsley [7], this metric is denoted by $d_0.$ With $d$, $D$ is a complete, separable metric space. Let $\mathcal{D}$ be a class of Borel sets of $D$. Then, if $P_n$ and $P$ are probability measures on $\mathcal{D}$ which satisfy:

for every bounded, continuous, real-valued function $f$ on $D$, we say that $P_n$ weakly converges to $P$, as $n\to \infty$, and write $P_n\Rightarrow P.$ A random function $X$ is a measurable mapping from some probability space ($\mathrm{\Omega },\mathcal{B},\mathcal{P}$) into $D$ having the distribution $P=\mathcal{P}{X}^{-1}$ on ($D,\mathcal{D}$). We say that a sequence of random functions $\left\{X_n\right\}$ weakly converges to the random function $X$, and write $X_n\Rightarrow X$, if the distribution $P_n$ of $X_n$ weakly converges to the distribution $P$ of $X$. A sequence of random functions $\left\{X_n\right\}$ converges to $X$ in probability, if $X_n$ and $X$ are defined on a common domain and for any $\epsilon >0$, $P\left\{d\right(X_n,X)\ge \epsilon \}\to 0.$ When $X$ is a constant function (not random), the convergence in probability is equivalent to a weak convergence. In such cases, we write $d(X_n,X)\Rightarrow 0$ or $X_n\Rightarrow X$. If $X_n$ and $Y_n$ have a common domain, we also write $d(X_n,Y_n)\Rightarrow 0$, when for all $\epsilon >0$, $P\left\{d\right(X_n,Y_n)>\epsilon \}\to 0$. We also use the uniform metric $\rho$ which is defined by $\rho (x,y)=\underset{0\le t\le 1}{\mathrm{s}\mathrm{u}\mathrm{p}}\left|x\right(t)-y(t\left)\right|$ for $x,y\in D$. Also, note that $d(x,y)\le \rho (x,y)$ for $x,y\in D$.

2. Statement of the problem

In this paper, we state that queue in series is a $k$-phase system, when $k\ge 2$. We investigate a $k$-phase queue in series (i.e., $k$-phase queue means that the system has $k$ servers connected sequentially in such a way, that the customer after being served by the $j$-th server, goes to the $(j+1)$-th server, while $j<k$, or leaves the system when $j=k$). Denote the phase of the queueing system by the sum of the waiting time of the customer and the service time of the customer. Let us denote $t_m$ as a time of arrival of the $m$-th customer, $S_m^{\left(j\right)}$ as a service time of the $m$-th customer in the $j$-th phase of a queue in series; $z_m=t_{m+1}-t_m$. Let us introduce independent renewal processes $x_j\left(t\right)=\{\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}:{\sum }_{i=1}^k‍S_i^{\left(j\right)}\le t\}$ (the number of customers that can be served in the $j$-th phase of the queues in series in the interval $[0,t]$ if devices are working without time waste), $e\left(t\right)=\{\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}:{\sum }_{i=1}^k‍z_i\le t\}$ (the number of customers who arrive to the queues in series in the interval $[0,t]$. Next, denote by ${\tau }_j\left(t\right)$ the number of customers that were served at the $j$-th phase in the interval $[0,t]$, $j=\mathrm{1,2},\dots ,k$, $t>0$.

Suppose that the virtual waiting time of the customer in each phase of the queues in series is unlimited, the discipline service of customers is “first come, first served” (FCFS). All random variables are defined in one common probability space ($\mathrm{\Omega },\mathcal{F},\mathcal{P}$).

Let interarrival times $\left(z_m\right)$ to the queues in series and service times $\left(S_m^{\left(j\right)}\right)$ in each phase of the queues in series as $j=\mathrm{1,2},\dots ,k,$ be mutually independent identically distributed random variables.

Assume:

Also, denote by $W_j\left(t\right)$ a virtual waiting time of arrival of the customer up to the $j$-th phase of the queues in series at time $t$ (the total virtual waiting time of a customer), by $V_j\left(t\right)$ – a virtual waiting time of the customer in the $j$-th phase of the queues in series at time $t$ (the time one must wait until a customer arrives at the $j$-th phase of the queues in series to be served); and by $S_j\left(t\right)$ the time of service of customers, arriving at the $j$-th phase of the queues in series in the interval $[0,t]$, $j=\mathrm{1,2},\dots ,k$, $t>0.$ Note that $W_j\left(t\right)=\sum _{i=1}^j‍V_i\left(t\right)$, $j=\mathrm{1,2},\dots ,k$, $t>0.$$W_j\left(t\right)$ can be interpreted as a continuous analog of the sojourn time process, $j=\mathrm{1,2},\dots ,k$, $t>0$ [12].

Note that $S_j\left(t\right)=\sum _{i=1}^{{\tau }_{j-1}\left(t\right)}‍S_i^{\left(j\right)}$, $j=\mathrm{1,2},\dots ,k$, $t>0.$

Also, let:

If $V\left(0\right)=0$ (a queueing system at time 0 is empty), then [13]:

Let us consider a sequence of queues in series as in Minkevičius [14]: we assume that sequences of queues in series tend to grow to infinity as $n\to \infty$. Thus, $S_{m,n}^{\left(j\right)}$ are identically distributed random variables in the $n$-th queues in series, $j=\mathrm{1,2},\dots ,k$, $S_{m,n}^{\left(0\right)}=z_{m,n}\text{,}$$m\ge 1$, $n\ge 1.$

Define $G_{j,n}\left(x\right)=P(S_{m,n}^{\left(j\right)}<x)$, ${\widehat{\alpha }}_{j,n}=E{S}_{m,n}^{\left(j\right)}$, $j=\mathrm{0,1},2,\dots ,k$, ${\beta }_n=\underset{1\le j\le k}{\mathrm{m}\mathrm{i}\mathrm{n}}{\beta }_{j,n}.$

Let:

and:

Note that, if ${\beta }_n>0$, then ${\beta }_{j,n}>0,j=\mathrm{1,2},\dots ,k$ and ${\widehat{\alpha }}_{k,n}>{\widehat{\alpha }}_{k-1,n}>\cdots >{\widehat{\alpha }}_{1,n}>{\widehat{\alpha }}_{0,n}>0.$ It must be mentioned that, under conditions of heavy traffic, ${\beta }_n>0$ and ${\beta }_n\to 0$, $n\to \infty$ [15].

3. The main results

First, we prove a functional limit theorem on the maximum of the total virtual waiting time of a customer in queues in series.

Theorem 3.1. If conditions Eq. (1) and (2) are fulfilled, then:

where $y_j\left(t\right)=\sum _{i=1}^j‍\{{\sigma }_i\cdot z_i(t\left)\right\}$ and $z_j\left(t\right)$ are independent standard Wiener processes, $j=\mathrm{1,2},\dots ,k$, $0\le t\le 1.$

Proof. Denote a family of random functions in $D$ as follows:

Applying a triangle inequality, we obtain that for $j=\mathrm{1,2},\dots ,k$:

But:

Therefore, from this and Eq. (3) we achieve that:

Finally, from Eq. (4) we obtain that:

The proof that [16]:

Also, note that for $i=\mathrm{1,2},\dots ,k$:

If Eqs. (1) and (2) are satisfied, then:

where ${\widehat{z}}_j\left(t\right)$, $j=\mathrm{1,2},\dots ,k$ and $t>0$ are Wiener processes with a positive endless drift.

Moreover, applying a continuous mapping theorem [7], we obtain that:

Thus, we prove that:

if conditions Eq. (2) are fulfilled.

The method for proving Eq. (10) is the same as applying the formula from Harrison’s book, [15]. For any $\epsilon >0$ and $\beta =-\infty$, we obtain:

where $\mathrm{\Phi }(\cdot )$ is a normal distribution function, $j=\mathrm{1,2},\dots ,k$ and $t>0.$

Note that if $z\left(0\right)=0,$ then $\underset{0\le s\le t}{\mathrm{s}\mathrm{u}\mathrm{p}}{\widehat{z}}_j\left(t\right)\ge 0$, $j=\mathrm{1,2},\dots ,k$ and $t>0.$ Consequently:

Thus:

which proves Eq. (10). Thus (see again a continuous mapping theorem):

from Eqs. (11) and (7) we achieve that $\rho ({\stackrel{-}{N}}_j^n,{\widehat{N}}_j^n)\Rightarrow 0$, $j=\mathrm{1,2},\dots ,k.$

Finally, proving:

is similar to Eqs. (8)-(12).

We denote $X~Y$, if the random variables $X$ and $Y$ have the same distribution function. It is clear, that:

If conditions Eq. (2) are satisfied, then, similarly as in Eqs. (8)-(12), we can prove that:

Again, by applying a continuous mapping theorem to the supremum function, we obtain that:

It follows, that:

From Eqs. (4), (12) and (15) we obtain that $d(W_j^n,M_j^n)\Rightarrow 0$, $j=\mathrm{1,2},\dots ,k.$ However [13]:

where $z_i\left(t\right)$ are independent standard Wiener processes, $j=\mathrm{1,2},\dots ,k$, $0\le t\le 1$.

Hence and applying Eqs. (2) we derive that:

In order to secure a multivariate weak convergence, it suffices for individual components of a limit process to be continuous in [0,1] [14]. Therefore, the proof is complete.

Next, we prove a functional limit theorem on the maximum of the virtual waiting time of a customer in queues in series.

Theorem 3.2. If conditions Eqs. (1) and (2) are fulfilled, then:

where $z_j\left(t\right)$ are independent standard Wiener processes, $j=\mathrm{1,2},\dots ,k$, $0\le t\le 1.$

Proof. The proof is similar to that of Theorem 3.1, and we omit it. The proof is complete.

4. Final note on the theorems

If all the servers in the queues in series configuration are asymptotically busy at all the phases, the service processes at different phases are asymptotically independent and form the differences of independent renewal processes. Thus, the processes $z_j\left(t\right)$, $j=\mathrm{1,2},\dots ,k$, $0\le t\le 1$ in Theorems 3.1, 3.2 are independent.

5. Computational simulation

In this section, we provide a simulation to illustrate an intuitive queues in series network model. We use “Simul8” software to imitate model’s behavior.

In order to simulate heavy traffic conditions, we choose an input of independent identically distributed process, having constant mean and standard deviation. The network model has an increasing virtual waiting time in each of the evolving phase of the network. In further examples, theoretical models with 2, 4 and 24 servers will be presented. In all of the network configurations, a constantly decaying service rate is set for each server in order to decrease $x_j\left(t\right)$ (the number of customers that can be served in the $j$-th phase of the network in the interval $[0,t]$). E.g., in 2-server configuration with arrival rate of 100 customers/minute and ${\sigma }^2=\text{25}$ standard deviation, service rates are set as ${\widehat{\alpha }}_1=E{S}_n^{\left(1\right)}=\text{90,}$ and ${\widehat{\alpha }}_2=E{S}_n^{\left(2\right)}=\text{80,}$ which satisfies the main requirement for heavy traffic, ${\beta }_j={\widehat{\alpha }}_j/{\widehat{\alpha }}_{j-1}-1>0$.

One can notice from the Fig. 1, that in the first phase the network is working in almost full capacity with some of the customers stopped due to heavy traffic, whilst in the second phase the server is utilized only by 67 percent, with more customers stopped (6.6 percent) and most of the customers waiting to be served (26 percent).

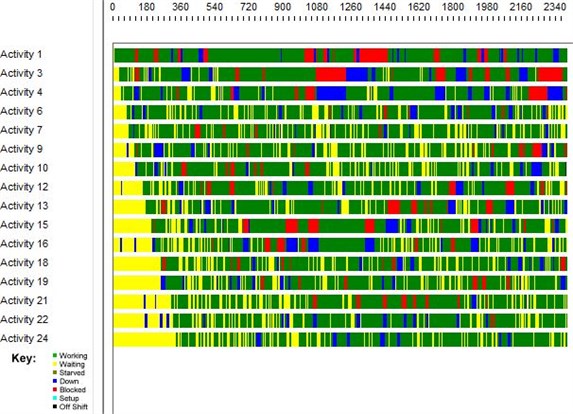
Timeline decomposition (Fig. 2) illustrates the periods of waiting and service times between each server in the network more clearly. Further, we provide graphical illustrations from the queues in series network model with 4 and 24 phases, accordingly (Figs. 3-6).

Graphical results show the same network behavior as in 2-server queues in series configuration, with an increasing virtual waiting time with each evolving phase of the network.

Fig. 12-server model of queues in series

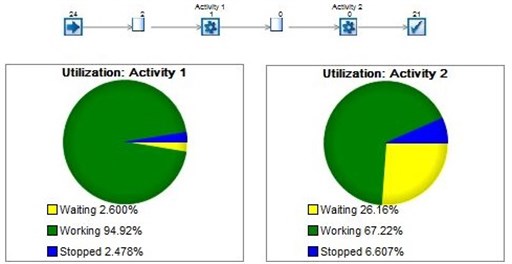
Fig. 2Timeline decomposition of 2-server queues in series

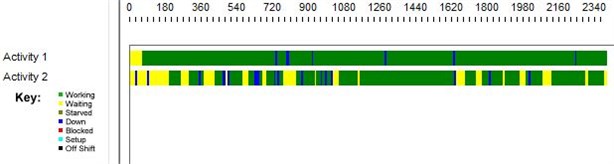
Fig. 34-server model of queues in series

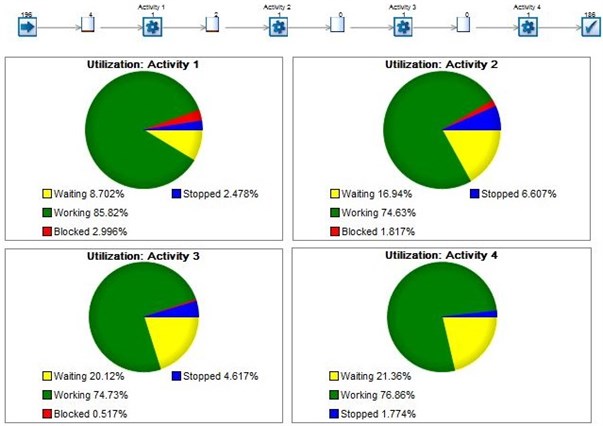
Fig. 4Timeline decomposition of 4-server queues in series

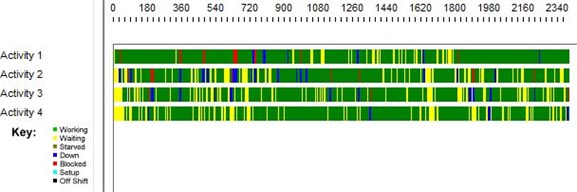
Fig. 524-server model of queues in series

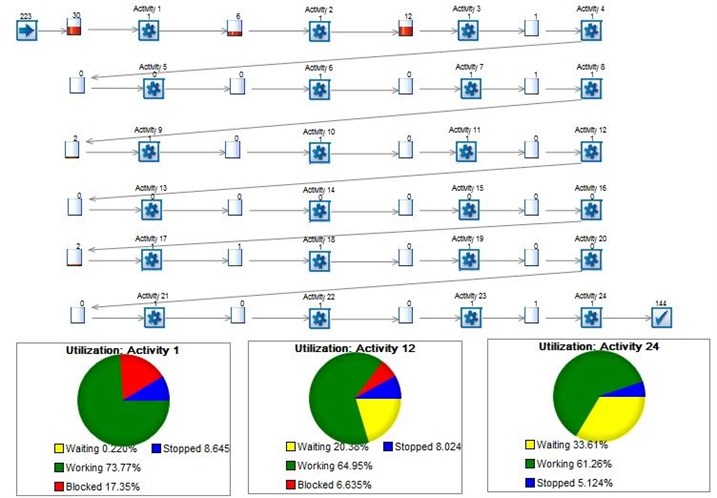
Fig. 6Timeline decomposition of 24-server queues in series

6. Conclusions

All the provided examples show that the queue of customers and the virtual waiting time grows indefinitely when the network of queues in series operates under conditions of heavy traffic. That proofs the operation of theoretical model described in this paper.