Vibration research of heavy trucks. Part 2: Optimization of vehicle dynamic parameters

2.1. The dynamic model of heavy trucks

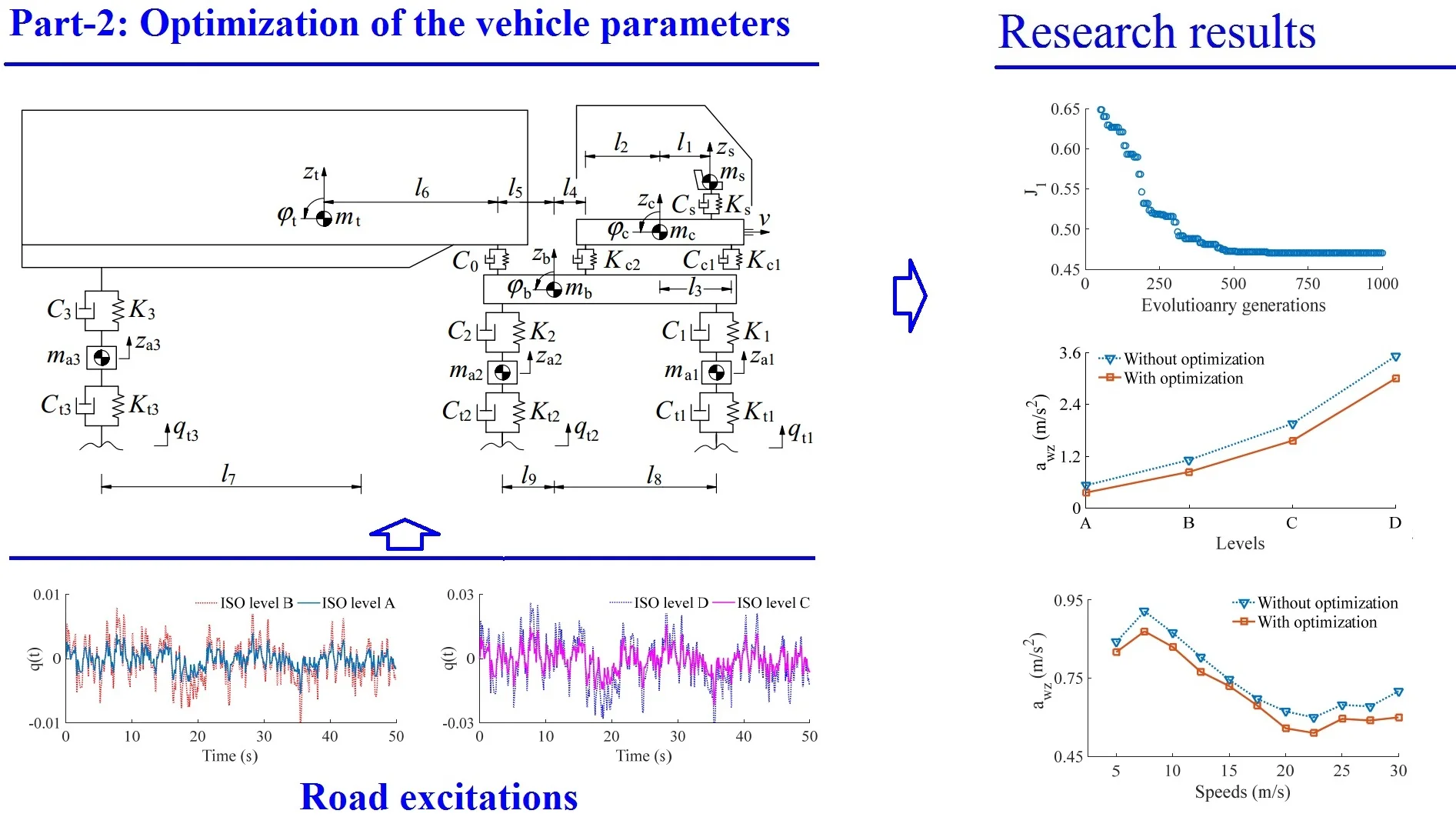
Based on research results in Part-1, the dynamic parameters of the vehicle suspension system with the vehicle dynamic model are plotted in Fig. 1, where, $z_s$, $z_c$, $z_b$, $z_t$, and $z_{ai}$ are the displacements in the $z$-direction of the seat, cab, body, trailer, and axle; ${\phi }_c$, ${\phi }_b$, and ${\phi }_t$ are the pitch angles of the cab, body, and trailer, respectively; $C_s$, $C_{cn}$, $C_i$, and $C_{ti}$ are the damping parameters of the suspension systems of the seat, cab, vehicle, and wheel, respectively; $K_s$, $K_{cn}$, $K_i$, and $K_{ti}$ are the stiffness parameters of the suspension systems of the seat, cab, vehicle, and wheel, respectively; $m_s$, $m_c$, $m_b$, $m_t$, and $m_{ai}$ are the mass of the seat, cab, body, trailer, and vehicle’s unsprung; $l_m$ are all geometric dimensions ($i=$ 1,…,3, $n=$ 1, 2, $m=$ 1,…, 9).

Fig. 1Lumped parameter model of heavy trucks

Based on the lumped parameter model of the vehicle in Fig. 1 and Newton-II law, the motion equations of the vehicle is represented by the matrix form as in Eq. (1):

where $M$, $C$, $C_a$, and $K$ are the matrices of the mass, passive damping, active damping, and stiffness of the vehicle, $Z$ is the displacement vector, and $F_q\left(t\right)$ is the excitation force vector of the vibrations from the road surface.

2.2. Road surface roughness

Based on the established method of the random road surface in Section 3 of Part-1, and according to the standard ISO 8068 [15], four types of level A to D of the road surface roughness are established and simulated at 72 km/h, as shown in Fig. 2. The excitation of these road surfaces is then applied for the simulation process of the vehicle.

Fig. 2Road profiles according to ISO 8068

2.3. Evaluation criteria of ride comfort

According to the ISO 2631-1 [16], the influence of the vibration on the driver’s health and ride comfort had been mainly assessed through the weighted RMS (Root-Mean-Square) of the acceleration responses, and it is described as follows:

where $a_z$ and $a_{\phi c}$ are the acceleration responses of the driver’s seat and cab that depend on the time of measurement $T$.

The weighted RMS acceleration responses of the vertical driver’s seat and the pitch angle of the cab of heavy trucks can be calculated from Eq. (2), their values are then compared with $a_{wz}$, as given in Table 1.

3.1. Multi-objective genetic algorithm (MGA)

The MGA is a multi-optimization method via the natural selection, and it is defined as finding the Maximum or Minimum functions of one or more goals. Thus, the MGA is simply described by the mathematical method as follows [5, 17-18]:

Find the vector $a={\left[a_1,a_2,\dots ,a_n\right]}^T$ for the optimization of the function $M\left(a\right)$:

Subject to $g_i\left(a\right)\le$ 0, $i=$ 1, 2,…, $p$, $h_j\left(a\right)=$ 0, $j=$ 1, 2,..., $q$, where $M\left(a\right)$ is the vector of the study goals, and $M\left(a\right)$ must be obtained the Maximum or Minimum values. $p$ and $q$ are the boundary conditions of the optimal regions.

The MGA structure has been defined by the steps of “encoding, population initialization, fitness evaluation, parent selection, genetic operations (crossover and mutate), and termination criterion”. Therefore, a flowchart of the MGA program for the optimization of the vehicle dynamic parameters is plotted in Fig. 3.

3.2. Application of the GA for optimization of the vehicle dynamic parameters

The goal of this study to apply the MGA is to optimize the parameters $\left\{C_s,C_{cn},C_i,C_{ti}\right\}$ and $\left\{K_s,K_{cn},K_i,K_{ti}\right\}$ of the damping and stiffness of the suspension systems of the seat, cab, vehicle, and wheel to reach the Minimum values of the weighted RMS values of the driver’s seat vibration ($a_{wz}$) and cab’s pitch vibration ($a_{w\phi c}$) via the lumped parameter model of the vehicle and the AGA model in Figs. 1 and 3. Therefore, the MGA’s structure has been established as follows:

(1) Encoding and initial populations: The dynamic parameters of $\{C_s,C_{cn},C_i,C_{ti}\}$ and $\left\{K_s,K_{cn},K_i,K_{ti}\right\}$ are connected to the chromosome regarded as the vectors to reduce the length of the chromosome and enhance the seeking speed of the AGA. Besides, the initial population, the generated individuals is random. With each gene, it is also randomly chosen in its region. In this study, the initial population size is established by 200.

Fig. 3The flowchart of the MGA

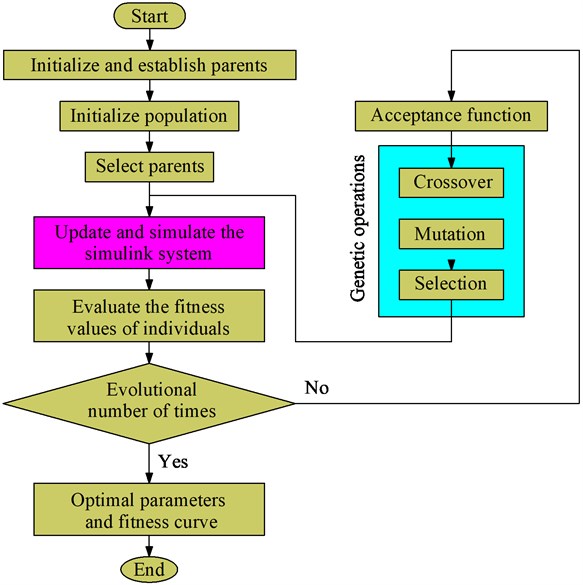
(2) Research values and fitness functions: In this study, the Minimum RMS values of the acceleration vibrations of the driver’s seat ($a_{wz}$) and cab ($a_{w\phi c}$) given in Eq. (2) have been chosen as the study aims. To research the Minimum RMS values of the acceleration vibrations, two fitness values of $J_1$ and $J_2$ are simplified to compute the study aims as follows [5]:

The individuals with the smaller fitness values $J_1$ and $J_2$ which are obtained via the subsystem model indicate that the obtained dynamic parameters are the better. Thus, the individuals have been updated before the evolution process ends, and the optimal result of the individuals is obtained.

(3) The process of genetic operations: Herein, the genetic operations have two process including crossover and mutation operations. This study chooses the crossover probability of 0.95 and mutation probability of 0.05 in $n=$ 1000 generations for the process of genetic operations. In the mutation operation of each individual with a probability of 0.05, the new individual is then generated and added in the population. Finally, based on two fitness values of $J_1$ and $J_2$, only the better individuals have been selected to perform next generations. For the termination criterion, it is happen when the change of the $J_1$ or $J_2$ between two adjacent generations below 10^-3, and the results of the congregation are then obtained. The MGA code is given in Table 1.

4.1. Optimal results

To find the optimal parameters for the heavy trucks, assuming that the vehicle travels under a random road surface of ISO level B at 72 km/h forward speed. The vehicle’s parameters as listed in Table 2 and its road surface excitation as plotted in Fig. 2 are chosen as the parameter inputs of the optimal model in Fig. 3. Additionally, based on the research results in Part-1, an optimal range of the vehicle dynamic parameters proposed to improve the vehicle ride comfort in Table 3 are used to limit the boundary conditions of the MGA. Therefore, the boundary conditions of the dynamic parameters for the MGA model are listed in Table 4. The MGA is then performed to find the optimal values of $J_1$ and $J_2$ in $n=$ 1000 generations.

Fig. 4The curve of fitness values of the AGA

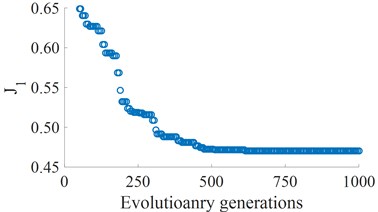
a) The fitness of the driver’s seat vibration

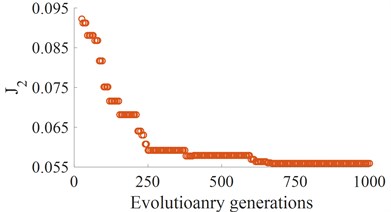
b) The fitness of the cab pitch vibration

According to the optimization code of the basic genetic algorithm programs in Table 1 [19], an optimal program of the heavy truck dynamic model is developed and applied to find the minimum values of the $a_{wz}$ and $a_{w\phi c}$. The results of the optimal running process are shown in Fig. 4. The results show that the Minimum fitness values of $J_1$ and $J_2$ are reached from the value 700 of evolutionary generation to the end. Thus, the optimization of the individuals is also obtained at the value 700 of generation. By decoding, the optimized values of the stiffness and damping parameters are presented in Tables 5 and 6. The optimal values of the vehicle dynamic parameters are then used to compute and assess the optimal performance.

Based on the optimal results of vehicle parameters, the simulated results of the vehicle with the optimal parameters are simulated and compared with the original parameters under the same simulation conditions. The acceleration vibrations of the vertical driver’s seat and cab’s pitch angle; and their weighted RMS acceleration responses ($a_{wz}$ and $a_{w\phi c}$) are plotted in Fig. 5 and listed in Table 7. As shown in Figs. 5(a) and (b), the vertical driver’s seat and cab’s pitch angle accelerations with the optimal parameters of heavy trucks are significantly reduced in comparison without optimization. The obtained results in Table 7 showed that the weighted RMS accelerations of the $a_{wz}$ and $a_{w\phi c}$ are significantly reduced by 26.3 % and 35.3 %. According to the standard ISO 2631-1 (Table 1 of Part-1) [16], the driver felt a little not uncomfortable. Thus, the ride comfort of heavy trucks is remarkably improved by the optimization of the vehicle dynamic parameters on ISO lever B. To evaluate the optimal performance of the vehicle dynamic parameters under different simulation conditions, the different road surfaces and speeds are simulated and analyzed below.

Fig. 5Optimal results of the acceleration vibrations of the cab and seat

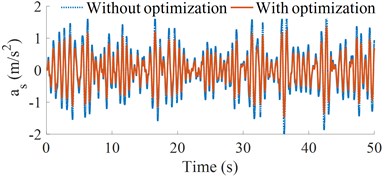
a) Driver’s seat vertical acceleration

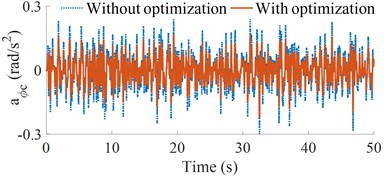
b) Cab pitch acceleration

Fig. 6Result of the weighted RMS accelerations of the cab and seat under various road surfaces

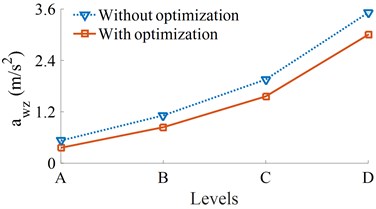
a) Driver’s seat vertical acceleration

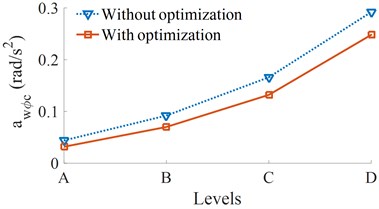
b) Cab pitch acceleration

4.2. The optimal result under various road surfaces

At the speed of the vehicle moving 72 km/h, four different road surface roughness of ISO level A (very good) to ISO level D (poor) have been used to evaluate the effect of road surface roughness on the effectiveness of the optimal parameters. The results of the $a_{wz}$ and $a_{w\phi c}$ are shown in Fig. 6. It can see that all their values are significantly reduced compared to without optimization. Thus, with the optimal parameters, the vehicle ride comfort has been also enhanced under different simulation conditions of the road surfaces.

4.3. The optimal result under various vehicle speeds

The simulation of the vehicle with its optimal parameters over a range of vehicle velocities under the road surface roughness of the level B is plotted in Fig. 7.

Fig. 7Result of the weighted RMS accelerations of the cab and seat under various vehicle speeds

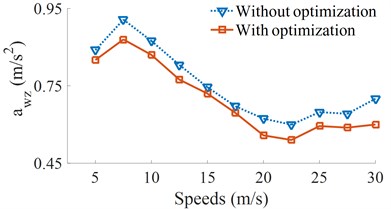
a) Driver’s seat vertical acceleration

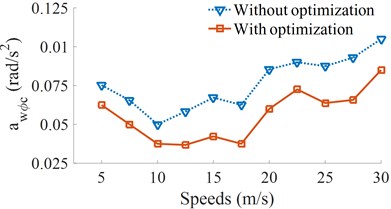
b) Cab pitch acceleration

Figs. 7(a) and (b) show that the $a_{wz}$ and $a_{w\phi c}$ of heavy trucks are significantly reduced in comparison without optimization in all the different speed conditions of heavy trucks. The research result also shows that the speeds of heavy trucks strongly affect the vehicle ride comfort. Within the speed region from 5 m/s to 15 m/s (18 km/h to 54 km/h) of the vehicle traveling, the weighted RMS acceleration of the vertical driver’s seat is strongly increased, while the weighted RMS acceleration of the cab’s pitch angle is minimum. It means that the cab shacking is improved, but the driver ride comfort is increased, thus, the drive feels uncomfortable when the vehicle moving at low speeds.

It is also found that the $a_{wz}$ and $a_{w\phi c}$ are significantly reduced at the speed from 17.5 m/s to 22.5 m/s (63 km/h to 81 km/h). It implied that the ride comfort of heavy trucks is clearly improved. On the contrary, with the increase of accelerations the speeds from 25 m/s to 30 m/s (99 km/h to 108 km/h), all the $a_{wz}$ and $a_{w\phi c}$ are increased, thus, the vehicle ride comfort is reduced. Based on the analysis results, a range of the vehicle speed from 17.5 m/s to 20 m/s (63 km/h to 72 km/h) should be used to more enhance the ride comfort of heavy trucks.