Influence of hydraulic engine mounts on engine shake based on full vehicle model

Guo, Rong; Gao, Jun; Wei, Xiaokang

Vibroengineering Procedia

Browse Procedia

Published: 08 December 2016

Check for updates

Influence of hydraulic engine mounts on engine shake based on full vehicle model

Rong Guo¹

Jun Gao²

Xiaokang Wei³

^{1, 2, 3}Clean Energy Automotive Engineering Center, Tongji University, Shanghai, China

Corresponding Author:

Rong Guo

Cite the article Download PDF

Downloads 1450

Abstract

This work proposes a full vehicle model including hydraulic engine mounts (HEMs) to better describe the characteristics of the vehicle engine shake performance. The model consists of 14 degree of freedoms (DOFs), namely 6 of the powertrain, 1 of the fluid within the inertia track of the HEM, 3 of the car body and 4 of the unsprung mass. Simulation based on the model is performed to demonstrate how the powertrain mounting system including the HEM influences the frequency response of vehicle subjected to harmonic excitations from road.

1. Introduction

Present automotive industry is witnessing a neck to neck fight to produce highly developed models with better performance. One of the performance requirements is accurate engine shake models to give better evaluation of the influence on the ride comfort caused by powertrain systems. Some popular models for vehicle ride analysis have been implemented by many researchers. Wen-Bin Shangguan et al. [1] established a vehicle model with 13 Degree of Freedoms (DOFs). Based on the model, the vibration at the seat track is calculated with input from road profile. Feng Wang [2] compared and analyzed the vibration characteristics based on a 6 DOF powertrain model and 13 DOF model with the powertrain system. The simulation results based on the latter model coincided with the experiment results better.

However, the models they set up are based on the assumption that the powertrain are on the elastic support connected to the vehicle body, which means, only rubber mounts are taken into account. It is known that hydraulic engine mounts (HEMs) are widely used in cars, therefore it is necessary to study the vibration response of the vehicle body based on the engine shake models with the mounting system including HEMs.

Vilsecker J. [3] considered the powertrain and the body as two subsystems, with the HEM between them. Tao C et al. [4] established a 3 DOF model with powertrain system, and then demonstrated that HEMs could better cancel the vehicle vibration. Fukazawa M. et al. [5] developed a CAE method to predict the vibration transfer function of the HEM on a vehicle with sufficient precision. The models including HEMs and vehicle body are simple and not adequate for more accurate analysis.

This work focuses on providing more accurate engine shake model by replacing a rubber mount in the 13 DOF vehicle model with a HEM. Simulation based on the model is performed to evaluate the effect of the HEM on the engine shake performance by comparing the results obtained from the known 13 DOF model.

2. Full vehicle model with powertrain for engine shake analysis

2.1. Mechanical model of the HEM

The linear mechanical model of HEM for the vertical vibration analysis under low frequency and large amplitude excitations is established, as shown in Fig. 1. The parameter $m_{i}$ , $b_{i}$ , $A_{i}$ , $X_{i}$ denotes the effective fluid mass in the inertia track, the damping coefficient for the linear fluid motion, the area of the inertia track, and the linear displacement of the fluid in the inertia track. $A_{p}$ , $k_{r}$ , $b_{r}$ represents equivalent area of the upper chamber, stiffness and damping properties of the main spring. The compliance of upper chamber and lower chamber is defined as $C_{1}$ , $C_{2}$ . The transmitted force to the force is derived for the mechanical model to ensure this system is mathematically equivalent to the original system equations. Observing the transmitted force at each pin, the force equations are determined:

1

F_{T_{1}} = k_{r} X + b_{r} \dot{X}, F_{T_{2}} = k_{1} (X - \frac{A_{i}}{A_{p}} X_{i}) - k_{2} \frac{A_{i}}{A_{P}} X_{i} - m_{i} {\ddot{X}}_{i} - b_{i} {\dot{X}}_{i},

F_{T_{3}} = k_{2} \frac{A_{i}}{A_{i}} X_{i}, F_{T_{4}} = b_{i} {\dot{X}}_{i} .

Fig. 1Low frequency, large amplitude linear model

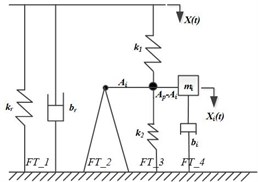
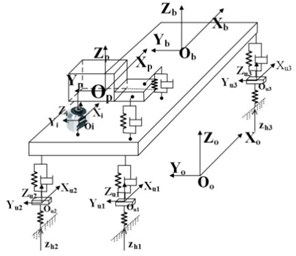
Fig. 2Full vehicle model including HEMs

2.2. Full vehicle model for engine shake including hydraulic engine mount

A 14 DOFs full vehicle model shown in Fig. 2 for the analysis of engine shake is proposed in this work. The model includes 6 DOFs of the powertrain, 3 DOFs of car body, 4 DOFs of the four unsprung mass, and 1 DOF of the fluid within the inertia track of the HEM.

In static equilibrium status, the following coordinate systems are defined. The Vehicle Coordinate System (VCS) is denoted with $O_{o}$ - $X_{o} Y_{o} Z_{o}$ ; the Powertrain Coordinate System (PCS) is denoted $O_{p}$ - $X_{p} Y_{p} Z_{p}$ ; the Car Body Coordinate system (BCS) is denoted with $O_{b}$ - $X_{b} Y_{b} Z_{b}$ . The origins of $O_{p}$ - $X_{p} Y_{p} Z_{p}$ and $O_{b}$ - $X_{b} Y_{b} Z_{b}$ are located at the center of gravity (CoG) of powertrain and car body, respectively. The coordinate systems for the unsprung mass (UCS)are denoted as $O_{u i}$ - $X_{u i} Y_{u i} Z_{u i}$ ( $i =$ 1,2, 3, 4) with its origin located at the CoG of each unsprung mass. The $X_{o}$ - and $Y_{o}$ - axis in the VCS are parallel to the horizontal plane, and $Z_{o}$ - axis is normal to the horizontal plane and the positive direction is upward. The positive $X_{o}$ - axis points to the rear of the vehicle. The $X_{p}$ -, $X_{b}$ -, $X_{i}$ and $X_{u j}$ - axes are parallel to $X_{o}$ - axis; the $Y_{p}$ -, $Y_{b}$ -, $Y_{i}$ - and $Y_{u j}$ - axes are parallel to the $Y_{o}$ - axis; the $Z_{p}$ -, $Z_{b}$ -, $Z_{i}$ and $Z_{u j}$ - axes are parallel to the $Z_{o}$ - axis, respectively. In static equilibrium, each dynamic coordinate system coincides with its fixed coordinate system. A right-hand Mount Coordinate System (MCS) denoted as $o_{i}$ - $u_{i} v_{i} w_{i}$ ( $i =$ 1, 2, 3, 4) is built for each mount, with its origin $o_{i}$ at the center of the mount. The stiffness and damping of the rubber mounts in $u_{i}$ -, $v_{i}$ - and $w_{i}$ - directions are $k_{u i}$ , $k_{v i}$ , $k_{w i}$ and $c_{u i}$ , $c_{v i}$ , $c_{w i}$ , while $k_{s 1}$ , $k_{s 2}$ , $k_{s 3}$ , $k_{s 4}$ and $c_{s 1}$ , $c_{s 2}$ , $c_{s 3}$ , $c_{s 4}$ are the stiffness and damping of the suspensions. $k_{t 1}$ , $k_{t 2}$ , k_t3. k_t4 denotes the stiffness of the tires.

The displacement excitation from ground to wheels is defined as $q_{h} = {(z_{h 1}, z_{h 2}, z_{h 3}, z_{h 4})}^{T}$ , and the displacements of CoGs for powertrain $m_{p}$ , car body $m_{b}$ and unsprung mass $m_{u i}$ are defined as $q_{p} = {(x_{p}, y_{p}, z_{p}, θ_{x p}, θ_{y p}, θ_{z p})}^{T},$ $q_{b} = {(z_{b}, θ_{x b}, θ_{x b})}^{T}$ and $q_{u} = {(z_{u 1}, z_{u 2}, z_{u 3}, z_{u 4})}^{T},$ respectively, where $T$ denotes the transpose of a vector. The displacement vector is defined as $q = {[q_{p}^{T}, q_{b}^{T}, q_{u}^{T}, z_{i}]}^{T}$ . The component in $q_{h}$ denotes the excitation to left front (LF) wheel, right front (RF) wheel, left rear (LR) wheel and right rear (RR) wheel, respectively. Displacement of the unsprung mass $i$ is defined as $z_{u i}$ . The component in $q_{b}$ represents the vertical displacement in $Z$ direction and angular displacement around $X$ and $Y$ directions; $θ_{x p}$ , $θ_{y p}$ , $θ_{z p}$ are the angular displacement around the $X$ , $Y$ , $Z$ directions respectively in the PCS. The coordinate system for the fluid in the inertia track of the HEM is defined as $O_{i}$ - $X_{i} Y_{i} Z_{i}$ with its origin located at the COG of the fluid mass.

2.2.1. The kinetic energy

The kinetic energy of the whole system consists of translational and rotational energy of vehicle body, as well as the translational energy of the wheels. The kinetic energy of the powertrain can be written as:

2

E_{T 1} = \frac{1}{2} \cdot m_{p} {\dot{x}}_{p}^{2} + \frac{1}{2} \cdot m_{p} {\dot{y}}_{p}^{2} + \frac{1}{2} \cdot m_{p} {\dot{z}}_{p}^{2} + \frac{1}{2} \cdot I_{x x} {\dot{θ}}_{x p}^{2} + \frac{1}{2} \cdot I_{y y} {\dot{θ}}_{y p}^{2}

+ \frac{1}{2} \cdot I_{z z} {\dot{θ}}_{z p}^{2} - \frac{1}{2} \cdot I_{x y} {\dot{θ}}_{x}_{p} {\dot{θ}}_{y p} - \frac{1}{2} \cdot I_{y z} {\dot{θ}}_{y p} {\dot{θ}}_{z p} - \frac{1}{2} \cdot I_{z x} {\dot{θ}}_{z}_{p} {\dot{θ}}_{x}_{p},

where the moments of inertia ( $I_{x x}$ , $I_{y y}$ , $I_{z z}$ ) and inertia products ( $I_{x y}$ , $I_{y z}$ , $I_{x z}$ ) of a powertrain are defined in the PCS.

Similarly, the kinetic energy of the body can be expressed as follows:

3

E_{T 2} = \frac{1}{2} \cdot m_{b} {\dot{z}}_{b}^{2} + \frac{1}{2} \cdot J_{x} {\dot{θ}}_{x b}^{2} + \frac{1}{2} \cdot J_{y} {\dot{θ}}_{y b}^{2},

where $J_{x}$ , $J_{y}$ denote moments of inertia of the body. The kinetic energy of the unsprung mass become:

4

E_{T 3} = \frac{1}{2} \cdot m_{u 1} {\dot{z}}_{u 1}^{2} + \frac{1}{2} \cdot m_{u 2} {\dot{z}}_{u 2}^{2} + \frac{1}{2} \cdot m_{u 3} {\dot{z}}_{u 3}^{2} + \frac{1}{2} \cdot m_{u 4} {\dot{z}}_{u 4}^{2} .

Assuming that there are $N$ HEMs in the mounting system, then the kinetic energy of the fluid in the inertia track $m_{i}$ is:

5

E_{T 4} = \sum_{i = 1}^{N} \frac{1}{2} m_{i} {\dot{z}}_{i}^{2},

where $z_{i}$ represents the displacement of the fluid. The total kinetic energy can be calculated:

6

E_{T} = E_{T 1} + E_{T 2} + E_{T 3} + E_{T 4} = 1 / 2 \cdot {\dot{q}}^{T} M \dot{q}

Eq. (6) can be expressed in the quadratic form:

7

E_{T} = \frac{1}{2} \cdot [\begin{array}{l} {\dot{q}}_{p} & {\dot{q}}_{b} & {\dot{q}}_{u} & {\dot{z}}_{i} \end{array}] \cdot d i a g (M_{p}, M_{b}, M_{u}, m_{i}) {[\begin{array}{l} {\dot{q}}_{p} & {\dot{q}}_{b} & {\dot{q}}_{u} & {\dot{z}}_{i} \end{array}]}^{T} .

2.2.2. The potential energy

The potential energy of the mounting system is:

8

E_{v 1} = 1 / 2 \cdot \sum_{i = 1}^{n} (k_{u i} Δ u_{i}^{2} + k_{v i} Δ v_{i}^{2} + k_{w i} Δ w_{i}^{2}) = 1 / 2 \cdot q^{T} K_{1}^{'} q .

The displacement of $m_{i}$ in $O_{i}$ - $X_{i} Y_{i} Z_{i}$ are defined as $x_{m i}$ , $y_{m i}$ , $z_{m i}$ , then the potential energy of the HEM become:

9

E_{v 2} = 1 / 2 \cdot k_{r} x_{m i}^{2} + 1 / 2 \cdot k_{r} y_{m i}^{2} + 1 / 2 \cdot k_{r} z_{m i}^{2} + 1 / 2 \cdot k_{1} (z_{m i} - A_{i} / A_{p} z_{i})^{2}

+ 1 / 2 \cdot k_{2} {(\frac{A_{i}}{A_{p} z_{i}})}^{2} = \frac{1}{2} \cdot q^{T} K_{2}^{'} q .

Similarly, the potential energy of the entire suspension system can be obtained:

10

E_{v 3} = \frac{1}{2} \cdot k_{s 1} Δ z_{s 1}^{2} + \frac{1}{2} \cdot k_{s 2} Δ z_{s 2}^{2} + \frac{1}{2} \cdot k_{s 3} Δ z_{s 3}^{2} + \frac{1}{2} \cdot k_{s 4} Δ z_{s 4}^{2} = \frac{1}{2} \cdot q^{T} K_{3}^{'} q .

The total potential energy of the tire system becomes:

11

E_{v 4} = \frac{1}{2} \cdot k_{t 1} Δ z_{u 1}^{2} + \frac{1}{2} \cdot k_{t 2} Δ z_{u 2}^{2} + \frac{1}{2} \cdot k_{t 3} Δ z_{u 3}^{2} + \frac{1}{2} \cdot k_{t 4} Δ z_{u 4}^{2} = \frac{1}{2} \cdot q^{T} K_{4}^{'} q .

As a result, the total potential energy of the 14DOF system proposed can be derived:

12

E_{v} = E_{v 1} + E_{v 2} + E_{v 3} + E_{v 4} .

Also, the stiffness matrix of the 14DOF system can be derived:

13

K = K_{1}^{'} + K_{2}^{'} + K_{3}^{'} + K_{4}^{'} .

2.2.3. The dissipation energy

The dissipation energy of the rubber mounts can be written as:

14

E_{D 1} = 1 / 2 \cdot \sum_{i = 1}^{N} (c_{u i} Δ {\dot{u}}_{i}^{2} + c_{v i} Δ {\dot{v}}_{i}^{2} + c_{w i} Δ {\dot{w}}_{i}^{2}) = 1 / 2 \cdot {\dot{q}}^{T} C_{1}^{'} \dot{q} .

The dissipation energy of the HEM can also be derived:

15

E_{D 2} = \frac{1}{2} \cdot b_{r} {\dot{x}}_{m i}^{2} + \frac{1}{2} \cdot b_{r} {\dot{y}}_{m i}^{2} + \frac{1}{2} \cdot b_{r} {\dot{z}}_{m i}^{2} + \frac{1}{2} \cdot b_{i} {\dot{z}}_{i}^{2} = \frac{1}{2} \cdot {\dot{q}}^{T} C_{2}^{'} \dot{q} .

The dissipation energy of the suspension system is:

16

E_{D 3} = \frac{1}{2} \cdot c_{s 1} Δ {\dot{z}}_{s 1}^{2} + \frac{1}{2} \cdot c_{s 2} Δ {\dot{z}}_{s 2}^{2} + \frac{1}{2} \cdot c_{s 3} Δ {\dot{z}}_{s 3}^{2} + \frac{1}{2} \cdot c_{s 4} Δ {\dot{z}}_{s 4}^{2} = \frac{1}{2} \cdot {\dot{q}}^{T} C_{3}^{'} \dot{q} .

Therefore, the total dissipation energy of the 14DOF system proposed can be described as:

17

E_{D} = E_{D 1} + E_{D 2} + E_{D 3} .

The stiffness matrix of the 14DOF system becomes:

18

C = C_{1}^{'} + C_{2}^{'} + C_{3}^{'} .

2.2.4. Response of the seat track

The transfer function between the inputs and outputs can be derived:

19

H (w) = \frac{q_{b} (w)}{q_{h} (w)} = (K - M \cdot w^{2} + j \cdot C \cdot w) \cdot K_{u},

where $H (w)$ is a (14×4) matrix, each column of which represents the response of the 14 DOF to the excitation at corresponding tires. Therefore, the transmissibility of vehicle body is $|H (w)|$ . Then the acceleration response magnitude becomes:

20

| H_{a} (w) | = | (j \cdot w)^{2} \cdot H (w) | = w^{2} \cdot |H (w)| .

Then acceleration response magnitude at the seat track becomes:

21

H_{a s t} (w) = H_{a}^{7} (w) + H_{a}^{8} (w) (r_{y s t} - r_{y b}) + H_{a}^{9} (w) (r_{x s t} - r_{x b}),

where $H_{a}^{7} (w)$ , $H_{a}^{8} (w)$ , $H_{a}^{9} (w)$ denote the 7th, 8th, and 9th row of $H_{a} (w)$ , respectively. $r_{x s t}$ , $r_{y s t}$ represents the $X$ axis and $Y$ axis coordinates of seat track in the VCS.

3. Simulation and analysis

The acceleration response magnitudes of the vehicle body under different inputs are calculated, as demonstrated in Fig. 3.

Fig. 3Acceleration response magnitude of the vehicle body under different inputs: a) RF wheel input; b) LF wheel input; c) RR wheel input; d) LR wheel input

Acceleration response magnitude of the vehicle body under different inputs: a) RF wheel input; b) LF wheel input; c) RR wheel input; d) LR wheel input

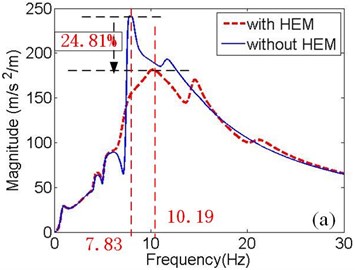
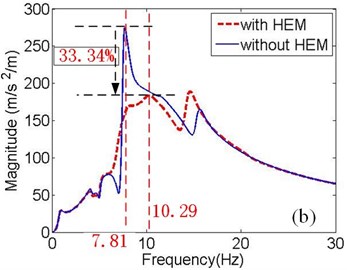
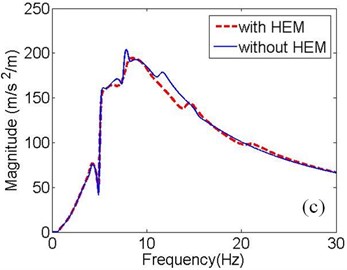
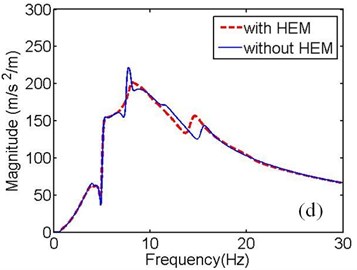
Fig. 3(a)-(b) illustrate that the magnitude of bounce resonance in the full vehicle model without HEMs is much higher than that in the 14 DOF model. After the engine rubber mount is replaced by HEM, the magnitude peak value of the acceleration response to the RF wheel and LF wheel input decrease by approximately 24.81 % and 33.34 % respectively. The HEM with high resistance is responsible for the restraint of the resonance, while the damping coefficients of rubber mounts are too small to mitigate the resonance. The resonant frequencies switch from 7.83 Hz to 10.19 Hz and from 7.81 Hz to 10.29 Hz respectively.

Fig. 3(c)-(d) show that the HEM has little influence on the response magnitude when the input is from RF wheel or RR wheel, for the reason that the curves are so close to each other. Therefore, the following analysis neglects evaluating the acceleration response to LR wheel and RR wheel inputs. Based on the above analysis, we derive the acceleration responses of seat track under right front and LR wheel inputs, which are shown in Fig. 4.

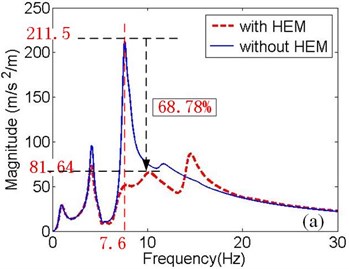
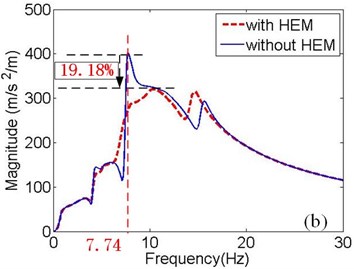
In Fig. 4(a), the bounce resonance at 7.6 Hz, dominates the curve when the powertrain is mounted without HEMs. However, when the mounting system features the HEM, the bounce resonance is severely restrained by up to 68.78 %. The resonance frequency switches to approximately 10 Hz. Compared with the green curve, the blue curve fluctuates more smoothly with a maximum value of 81.64. When the HEM is adopted, the maximum value in Fig. 4(b) is 3.97 times as much as that in Fig. 4(a). It can be seen that the resonance of the green curve at 7.74 Hz is limited by 19.18 % due to the damping of the HEM.

Fig. 4Acceleration response magnitude of the seat track under different inputs: a) RF wheel input; b) LF wheel input

4. Conclusions

In this work, a full vehicle model with 14 DOFs including the fluid in the inertia track of the HEM is proposed to calculate the engine shake at vehicle body and seat track. It is concluded that the mounting system with the HEM has greater restriction on the body and seat track shake subjected to front wheel inputs, compared with the mounting system simply with rubber mounts. Furthermore, the response magnitude due to LF wheel input is much higher than that due to RF wheel input for the reason that the HEM is at the right hand side of the powertrain.

References

Shangguan Wen-Bin, et al. Design method of automotive powertrain mounting system based on vibration and noise limitations of vehicle level. Mechanical Systems and Signal Processing, Vol. 76, 2016, p. 677-695.

Search CrossRef
Wang Feng, Jin Y. J., Zhang J. W. Vibration simulation and optimization of a powertrain mounting system based on a full vehicle model. Journal of Vibration and Shock Vol. 27, Issue 4, 2008, p. 134-138.

Search CrossRef
Vilsecker J., Mack W., Falkner A., et al. On the complexity of hydromount-models in full vehicle simulation. Proceedings in Applied Mathematics and Mechanics, Vol. 11, Issue 1, 2011, p. 341-342.

Search CrossRef
Tao C., Zhu H., Xu P., et al. Frequency-dependent hydraulic engine mount with five-parameters fractional derivative model in vehicle model. SAE Technical Papers, 2015.

Search CrossRef
Masahiro Fukazawa, Murao T., Unigame S. The method to predict the vibration transfer function of hydraulic engine mount on a vehicle. Aquichan, Vol. 4, Issue 4, 2009, p. 70-72.

Search CrossRef
Ms Trupti Bhoskar, et al. Genetic algorithm and its applications to mechanical engineering: a review. Materials Today: Proceedings, Vol. 2, Issue 4, 2015, p. 2624-2630.

Search CrossRef

About this article

Received

08 November 2016

Accepted

09 November 2016

Published

08 December 2016

SUBJECTS

Vibration in transportation engineering

Keywords

engine shake

full vehicle model

hydraulic engine mount

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.