A novel Pennes’ bioheat transfer equation with memory-dependent derivative

1. Introduction

The memory-dependent derivative is defined in an integral form of a common derivative with a Kernel function on a slipping interval [1]. Thus, this kind of definition is better than the fractional one for reflecting the memory effect (instantaneous change rate depends on the past state). Its definition is more intuitionistic for understanding the physical meaning and the corresponding memory dependent differential equation has more expressive force.

The fractional order calculus is more important in many applications in different areas of engineering and modern physics. We can use the fractional calculus to modify the classical Fourier law of heat conduction. The commonly used definition of fractional derivative is the Caputo type [2, 3]:

with:

where $b$ is a fixed real number, $m$ is an integer which satisfies $m-1<\alpha \le m$, $\mathrm{\Gamma }$ is the Euler’s Gamma function and $f^{\left(m\right)}$ is the common $m$-order derivative which has specific physical meaning and $K_{\alpha }(t-\xi )$ is the Kernel of function.

From Eq. (1), we see the $\alpha$-th order fractional derivative at time $t$ is not defined locally, it relies on the total effects of the commonly used $m$-order integer derivative on the interval [$a$, $t$]. So, it can be used to describe the variation of a system in which the instantaneous change rate depends on the past state, which is called “memory effect” in a visualized manner [4]. This is why the fractional theory is widely used.

The first order memory-dependent derivative of a function $f\left(\xi \right)$ was introduced by Wang and Li [1]. They defined it in an integral form of a common derivative with a Kernel of function on slipping interval in the form:

where $\omega$ is the time-delay parameter and $K(t-\xi )$ is the Kernel of function which can be chosen freely [5]. The Taylor theorem in terms of memory-dependent derivatives can found in [5] as:

where:

As in [5], we can expand the heat flux vector $\overrightarrow{q}(x,t+\omega )$ by Taylor’s series of memory-dependent derivative and neglected the terms up to the first order in time-delay $\omega$ to get:

Recently, an interesting application of memory-dependent derivative is given by Yu et al. [6]. They introduced the memory-dependent derivative (MDD) instead of fractional calculus into the rate of heat flux in Lord-Shulman theory [7] of generalized thermoelasticity to denote memory-dependence as:

Eq. (7) has more clear physical meaning.

In this paper, a new mathematical model for Pennes’ bioheat equation using the new memory-dependent derivative is established. The one-dimensional thermal behavior in living tissue subject to instantaneous surface heating is investigated. Numerical calculations are performed to study the temperature transients in the skin exposed to instantaneous surface heating. Numerical results are plotted in the form of two-dimensional graphs and discussed. In this novel model, the time delay parameter is a new indicator of bio-heat efficiency in living tissues.

2. Pennes’ bioheat transfer equation with memory-dependent derivative

Heat transfer in biological systems is usually modelled by the Pennes’ bioheat equation [8] based on the classical Fourier’s law (which specifies a linear relationship between heat flux and temperature gradient):

as:

where $T(\overrightarrow{x},t)$ is the temperature of living tissue and $Q(\overrightarrow{x},t)$ is the volumetric heat generated by metabolism and blood perfusion, given by:

where $G_B$ is the blood perfusion, $C_B$ is the volumetric specific heat of blood, $T_B$ is the artery temperature and $Q_m$ is the metabolic heat source. A well-known problem with Fourier’s law is that it yields infinitely fast propagation of thermal signal, incompatible with physical reality and physiological considerations in a transient process. This equation implies an instantaneous thermal energy deposition in medium, i.e. any local temperature disturbance causes an instantaneous perturbation in temperature at each point in medium.

As explained above, heat pulses obtained by the classical bio-heat conduction equation propagate at infinite speed. Much attention has been devoted to modifying the classical heat conduction equation to ensure finite speed pulse propagation. In mathematical terms, the governing partial differential equation is transformed from parabolic to hyperbolic type [9]. A general form of bioheat transfer model in living tissues based on the generalized Fourier’s law [7]:

can be put in the form:

where $\tau$ is a relaxation time parameter, $k$ is the tissue thermal conductivity and $C$ is the specific heat.

From a mathematical viewpoint, the Fourier’s law Eq. (8) for the considered new memory-dependent derivative with time-delay parameter $\omega$ is given by:

Taking the memory-time derivative of Eq. (9) (suppressing $\overrightarrow{x}$ for convenience), we get:

Multiplying Eq. (14) by $\omega$ and adding to Eq. (9), we obtain:

Substituting from Eq. (13) into the Eq. (15), we finally get:

Eq. (16) is the new bioheat transfer equation with memory- dependent derivative, taking into account the time-delay parameter$\omega$. The Pennes’ bioheat equation is follows as a limit case when $\omega \to 0$. This model is more intuitionistic for understanding the physical meaning and the corresponding memory dependent differential equation is more expressive.

3. Application

The temperature distribution in human skin with instantaneous surface heating for more understanding to the thermal wave propagation behaviour of fractional bioheat transfer equation is considered. One dimensional model of the FPBE in a finite medium was established. The predictions of the FPBE equation are then compared those of other representations of the Pennes’ equation, to reveal the distinct differences in heat transfer modelling processes.

The one-dimensional form of Eq. (16), given $Q_m$= constant, is written as:

Then the initial steady state temperature $T_0(x,0)$ in skin is derived from Eq. (17) as:

Subtracting Eq. (18) from Eq. (17), yields:

where the evaluation temperature $\theta (x,t)$ is defined as $\theta (x,t)=T(x,t)-T_0$.

In numerical solutions, we assume that heat flux approaches zero deep within the tissue $(x-d)$ as expected in biological body.

The homogeneous initial conditions are:

The appropriate boundary conditions are taken as:

From now on, the kernel function form $K(t-\xi )$ can be chosen freely as:

where $a$ and $b$ are constants.

4. The solution in Laplace transform domain

Appling the Laplace transform with parameter $p$ defined by the formula:

to both sides of Eq. (19) taking into account the initial conditions Eq. (20) and to the boundary conditions Eqs. (21), the equations become:

with the boundary conditions:

where:

Imposing the boundary conditions Eq. (21) upon the heat flow Eq. (24), the exact solution for the temperature distribution $\stackrel{-}{\theta }(x,p)$ in the Laplace transform domain is obtained as:

5. Numerical results and discussions

The Laplace transform in the above equation is inverted numerically by Zakian algorithm [10, 11]. Biological skin is a very complex heterogeneous medium, containing many different layers, each having their own unique thermal and blood perfusion properties.

Typical values of thermal properties for skin tissue and other parameters have been chosen as $\rho =$ 1000 kg/m³, $C=C_B=$ 4200 J/kg °C [12]. The distance between the skin and body core is $d=$ 0.01208 m and the surface temperature is taken as ${\theta }_0=$ 12 °C.

Fig. 1 shows that the effect of the time-delay parameter $\omega$ on the temperature distribution in living tissue. The time-delay parameter plays an important role in bioheat transfer. The heat energy taken away by the blood is directly proportional to the perfusion rate. Also, the skin temperature is maximum at $x=$ 0 for $\omega =$ 0.09. This research also provides some new points for studying transient heat transfer processes in biological systems.

Fig. 1Temperature distributions versus skin depth temperature for different values of time-delay ω and K(t-ξ)=1-(t-ξ) with k= 0.2 W/m °C, GB= 8.0 kg/m3s and at t= 250 s

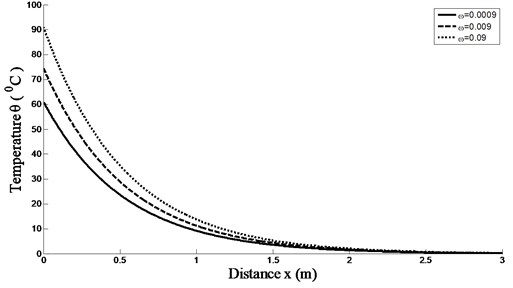
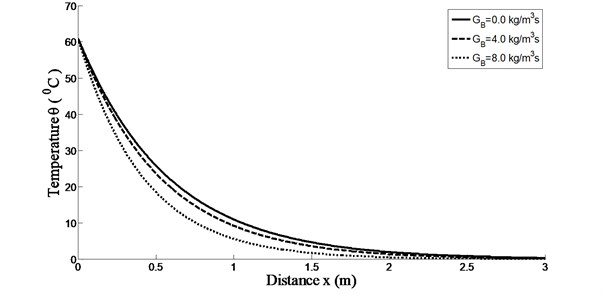
Fig. 2 depicts the effect of the perfusion rate of blood on the temperature distribution in living tissue. The perfusion rate of blood shows an important role in bioheat transfer. Since the skin temperature exceeds the arterial temperature, blood perfusion performs a cooling function. The heat energy extracted by the blood is proportional to the perfusion rate. It is clear from the Fig. 2 that the skin temperature for $G_B=$ 8.0 kg/m³s is lower than that for $G_B=$ 4.0 kg/m³s and $G_B=$0.0 kg/m³s. In this case the skin temperature also attains its maximum value at $x=\text{0}$.

Fig. 2Temperature distributions versus skin depth temperature for time-delay ω= 0.0009 and K(t-ξ)=1-(t-ξ) with k= 0.2 W/m °C and at t= 250 s for different blood perfusion rate GB

6. Conclusions

The main goal of this work is to introduce a new mathematical model for the Pennes’ bioheat transfer equation memory-dependent derivative involving time-delay parameter $\omega$. In this paper, the memory-dependent derivative is successfully incorporated into a bioheat transfer model. In an attempt to reconcile the novel and classical approaches to bioheat transfer, results of our model were compared with those of the classical and hyperbolic bioheat transfer equations

The Pennes’ bioheat transfer model with memory dependent derivative is established and applied to investigate the thermal response in living tissue with instantaneous surface heating. It is observed that thermal wave propagation may provide realistic prediction of temperature distribution in living tissue. The blood perfusion develops the cooling function to prevent the tissue rising, but does not affect the thermal propagation velocity. In this novel theory, we propose that the time-delay parameter$\omega$ becomes a new indicator of bioheat transfer efficiency in living tissues.