The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Youssef, Hamdy M.; Al Thobaiti, Abdullah A.

doi:10.21595/jets.2022.22568

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 30 June 2022

Check for updates

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Hamdy M. Youssef¹

Abdullah A. Al Thobaiti²

¹Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, 21955, Saudi Arabia

¹Mathematics Department, Faculty of Education, Alexandria University, Alexandria, Egypt

²Mathematical Department, Faculty of Applied Sciences, Umm Al-Qura University, Makkah, 21955, Saudi Arabia

Corresponding Author:

Hamdy M. Youssef

Cite the article Download PDF

Abstract

In this paper, a new analysis of thermoelastic, homogeneous, and isotropic nanobeams has been constructed in the context of the Green-Naghdi type-II heat conduction law. The first end of the nanobeam is based on a graphene strip, which contains an electrical current with a small voltage which is a novel application. Under simply supported boundary conditions with fixed side ratios, the nanobeam has been thermally loaded with a heat source due to the thermal effect of the electrical current. On the time variable, the Laplace transform technique was utilized to solve the governing differential equations. The solutions were computed in the Laplace transform’s domain. Tzou’s approximation technique based on an iteration formula was used to calculate the Laplace transform inversions numerically. The numerical findings for various values of the electrical voltage and electrical resistivity of the graphene nano-strip have been displayed using graphs illustrating distinct scenarios. All the nanobeam’s researched functionalities have been reported to be influenced by electrical voltage and electrical resistivity. The electrical voltage and resistivity of a graphene nano-strip might be utilized as a tuner to regulate the nanobeam's vibration and energy.

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Highlights

Green-Naghdi type-II heat conduction model has been applied to analyze thermoelastic microbeams in this study
The nano-strip of graphene at the microbeam's beginning end is connected by a low-voltage electrical current.
The extended thermoelasticity theory Lord-Shulman model was used.
Gradually increasing electrical voltage raises thermal and mechanical stress and strain energy density as well as the lateral deflection, stress and strain energy density values.
The graphene microstrip might be used as a tuner to regulate the vibration and energy of the microbeam by controlling the voltage and resistance of the microstrip.

1. Introduction

Thermoelasticity is a kind of heat transfer based on Fourier's law of heat transfer, which consists of two partial differential equations: one for motion and the other for energy conservation [1-4]. Lord and Shulman modified Fourier's rule of heat conduction in the case of an isotropic body by including the relaxation time in the equation [5]. The law of heat conduction (Cattaneo's heat conduction, also known as non-law Fourier’s of heat conduction) has been revised to incorporate both the heat flux and its time derivative, and it has been proposed to replace the traditional Fourier's law of heat conduction. The heat equation is hyperbolic in this theory, avoiding the problem of infinite propagation [6-11].

Green and Naghdi (G-N) proposed three different theories of thermoelasticity based on entropy equality rather than entropy inequality [9-11]. In each theory, the vector of the heat flux vector has a distinct constitutive consideration. As a result, Green-Naghdi type-I, Green-Naghdi type-II, and Green-Naghdi type-III were developed. The classical thermoelasticity system is the same as a type-I theory in linearized form. There is no energy dissipation in the type-II theory; instead, it is regarded as a specific instance of type-III, which contains energy dissipation in its definition [12-17].

Because it creates the most vibration, the vibration nanobeam resonator is the most important of the nano/micro-beam resonators. Alghamdi investigated thermoelastic damping vibration with gaps in a beam resonator using dual-phase-lagging generalised thermoelasticity theory [1]. On the micro/nanoscale, Sharma and Grover explored the transverse vibrations of homogeneous isotropic and thermoelastic thin beam resonators that contained voids [18]. Sun and Saka explored the thermoelastic damping vibration of circular plate resonators using out-of-plane microplates [19]. The vibration and heat transmission mechanisms of nanobeams have been studied by a significant number of writers [20-24]. Eman and Youssef studied the vibration of gold nanobeam due to thermal shock [21]. Kidawa investigated the effects of internal and external damping on transverse vibrations of a beam induced by a moving heat source using Green functions and their characteristics in his research [23]. A rectangular nanobeam with simple support was subjected to a thermal shock that was spread along its span, and Boley investigated the vibrations of the beam [22]. Manolis and Beskos investigated the elastic dynamic response of beam constructions to heat loading by using a computer approach study [24].

In mechanics, the study of viscothermoelastic materials, often known as relaxation characteristics, is becoming increasingly relevant. Biot has published on viscothermoelasticity theory and thermodynamic vibrational principles, among other topics [25, 26]. Drozdov devised a constitutive model for the viscothermoelasticity behaviour of polymers when they are exposed to finite stresses [27]. To study the relaxing effects of volume-features of viscoelastic materials thermoelasticity, Ezzat and El-Karmany used a novel thermo-viscoelasticity model for isotropic media devised by the authors [28]. Carcione et al. devised a numerical technique for wave simulations in elastic media based on the Kelvin-Voigt mechanical model [29]. Grover studied transverse vibrations in micro-scale viscothermoelastic beam resonators [30-32]. A homogeneous thermoelastic thin beam with vacancies on the micro/nano-scale was studied by Sharma and Grover in terms of closed-form equations for transverse vibrations [18]. Grover and Seth studied viscothermal elastic micro-scale beam resonators using a dual-phase lagging model [33].

Since the groundbreaking observations of Novoselov et al., graphene has continued to pique the interest of scientists around the world [34]. Single-layer graphene has exciting electrical features, including ballistic transport, a quantum Hall effect at ambient temperature, and a size-dependent band gap, all of which have the potential to allow new types of nanoscale electronic devices and sensors, such as transistors [35].

Green-Naghdi type-II heat conduction law has been used for the first time in this study to analyse thermoelastic, homogeneous, and isotropic nanobeams, which have a graphene strip as the initial end of the nanobeam linked to a low voltage electrical current. The nanobeam will become thermally loaded with a heat source as a result of the electrical current's thermal action on the low-voltage nano-graphene strip. The microbeam was electrically isolated using an electrical isolator with high thermal conductivity.

2. Problem formulation

We consider the flexural deflections are very small for a thin thermoelastic nanobeam of thickness $h (- h / 2 \leq z \leq h / 2)$ , width $b (- b / 2 \leq y \leq b / 2)$ , and length $l (0 \leq x \leq l)$ .

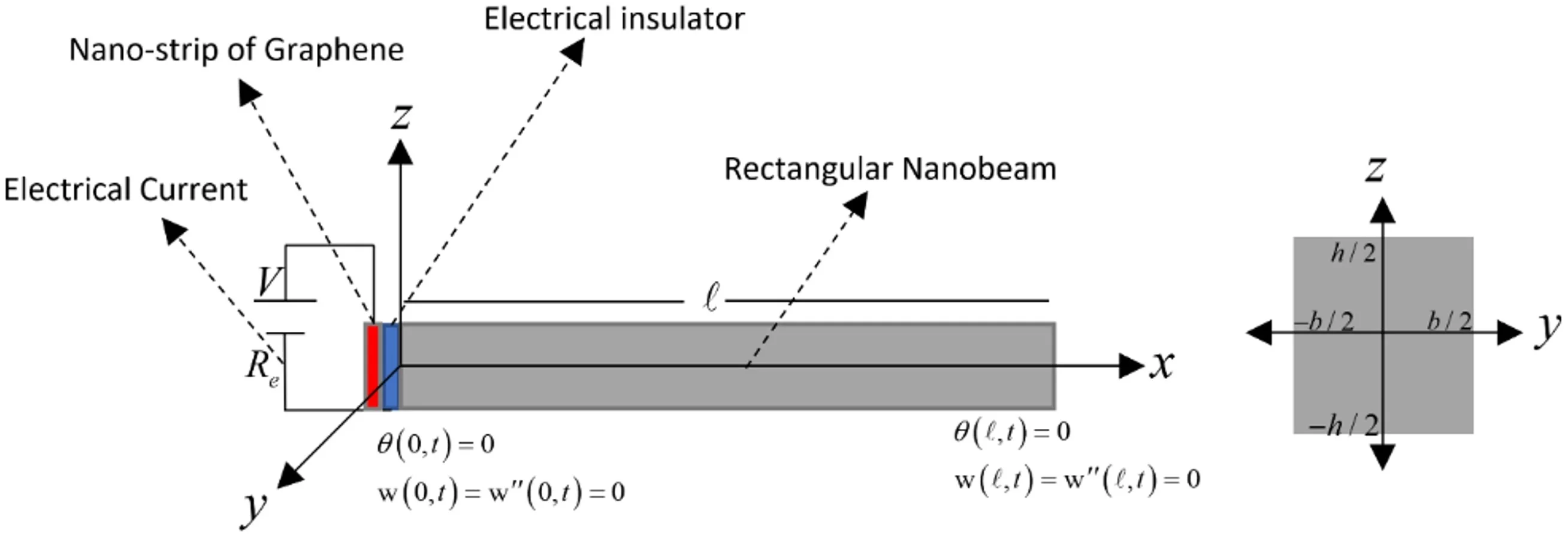
Fig. 1Rectangular thermoelastic nanobeam based on an electrical insulator and a nano-strip of graphene

The $x$ , $y$ , and $z$ -axes are defined through the longitudinal, width, and thickness directions of the beam as in Fig. 1.

In an equilibrium state, the nanobeam has no damping, unstressed, unstrained, and the reference temperature is $T_{0}$ everywhere [6].

Beam bending will use the Euler-Bernoulli equation, which states that any plane cross-section that is perpendicular to the beam’s axis (neutral surface) will stay so [30].

Then, the displacement components will take the forms [30, 32, 33, 36]:

1

u (x, y, z, t) = - z \frac{\partial w (x, t)}{\partial x}, v (x, y, z, t) = 0, w (x, y, z, t) = w (x, t) .

The flexural moment of the cross-section and equation of motion is given by [30, 32, 33, 36]:

2

M (x, t) = β M_{T} (x, t) + (λ + 2 μ) I \frac{\partial^{2} w (x, t)}{\partial x^{2}},

where the equation of motion takes the form:

3

\frac{\partial^{2} M (x, t)}{\partial x^{2}} + ρ A \ddot{w} (x, t) = 0 .

The thermal moment $M_{T}$ of the nanobeam about the x-axis is given by [30-33, 36, 37]:

4

M_{T} (x, t) = \int_{- h / 2}^{h / 2} b T (x, z, t) z d z,

where $I = b h^{3} / 12$ gives the moment of inertia of the cross-section around the $x$ -axis, $ρ$ is the density of the material, $A = h b$ is the cross-section area, $β = (3 λ + 2 μ) α_{T}$ , $λ$ and $μ$ are the elastic constant, and $α_{T}$ is the coefficient of linear thermal expansion.

Thus, the equation of motion which gives thermally induced lateral vibrations of the nanobeam takes the form [30]:

5

β \frac{\partial^{2} M_{T} (x, t)}{\partial x^{2}} + (λ + 2 μ) I \frac{\partial^{4} w (x, t)}{\partial x^{4}} + ρ A \ddot{w} (x, t) = 0 .

The Green-Naghdi type-II heat conduction equation takes the form [30]:

6

\frac{\partial^{2} T (x, z, t)}{\partial x^{2}} + \frac{\partial^{2} T (x, z, t)}{\partial z^{2}} = \frac{ρ C_{υ}}{K^{*}} \ddot{T} (x, z, t) + \frac{β T_{0}}{K^{*}} \ddot{e} (x, z, t) - \frac{Q (x, z, t)}{K^{*}},

where $K^{*} = (λ + 2 μ) C_{υ} / 4$ which is called the Green-Naghdi theorem parameter, $C_{υ}$ is the specific heat under constant strain, and $Q$ is the external heat source.

The cubical dilatation (volumetric strain) has the form:

7

e (x, z, t) = \frac{\partial u (x, z, t)}{\partial x} + \frac{\partial v (x, z, t)}{\partial y} + \frac{\partial w (x, z, t)}{\partial z} .

Thus, from the Eq. (1) we have:

8

e (x, z, t) = - z \frac{\partial^{2} w (x, t)}{\partial x^{2}} .

Then, we obtain:

9

σ_{x x} (x, z, t) = (λ + 2 μ) e (x, z, t) - β (T (x, z, t) - T_{0}) .

The upper and lower surfaces of the beam do not have heat transfer, so ${\frac{\partial T (x, z, t)}{\partial z}|}_{z = \pm \frac{h}{2}} = 0$ . Hence, for a nanobeam, we can postulate the temperature depends on a “ $s i n (p z)$ ” function through the thickness direction of the beam, where $p = π / h$ , which gives [38]:

10

θ (x, z, t) = T (x, z, t) - T_{0} = ϑ (x, t) s i n (p z),

and

11

Q (x, z, t) = q (x, t) s i n (p z),

where $θ (x, z, t)$ is devoted to the temperature increment.

Hence, from the Eqs. (4), (5), and (10), we obtain:

12

\frac{12 β}{h^{3} (λ + 2 μ)} \frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} \int_{- h / 2}^{h / 2} s i n (p z) z d z + \frac{\partial^{4} w (x, t)}{\partial x^{4}} + \frac{12 ρ}{h^{2} (λ + 2 μ)} \ddot{w} (x, t) = 0 .

By using Eqs. (6) and (10), we get:

13

(\frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} - p^{2} ϑ (x, t)) s i n (p z) = ε \ddot{ϑ} (x, t) s i n (p z) - \frac{T_{0} β}{K^{*}} z \frac{\partial^{2} \ddot{w} (x, t)}{\partial x^{2}} - \frac{q (x, t)}{K^{*}} s i n (p z),

where $ε = ρ C_{υ} / K^{*}$ which gives the thermal viscosity parameter of the material.

After executing the integrations, the Eq. (12) has the form:

14

\frac{24 β}{h π^{2} (λ + 2 μ)} \frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} + \frac{\partial^{4} w (x, t)}{\partial x^{4}} + \frac{12 ρ}{h^{2} (λ + 2 μ)} \ddot{w} (x, t) = 0 .

After re-write the Eq. (13), we obtain:

15

\frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} - p^{2} ϑ (x, t) = ε \ddot{ϑ} (x, t) - \frac{T_{0} β}{K^{*}} \frac{z}{s i n (p z)} \frac{\partial^{2} \ddot{w} (x, t)}{\partial x^{2}} - \frac{q (x, t)}{K^{*}} .

The Eq. (9) takes the form:

16

σ_{x x} = (λ + 2 μ) e - β ϑ s i n (p z) .

The following non-dimensional variables will be used [19]:

17

(x', w', h', l', z') = ε c_{0} (x, w, h, l, z), (t', τ') = ε c_{0}^{2} (t, τ),

σ^{'} = \frac{σ}{λ + 2 μ}, ϑ^{'} = \frac{ϑ}{T_{0}}, q^{'} = \frac{q}{T_{0} K^{*} ε^{2} c_{0}^{3}}, \begin{array}{l} c_{0}^{2} = \frac{λ + 2 μ}{ρ} \end{array} .

Then, we have:

18

\frac{\partial^{4} w (x, t)}{\partial x^{4}} + ε_{1} \ddot{w} (x, t) + ε_{2} \frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} = 0,

19

\frac{\partial^{2} ϑ (x, t)}{\partial x^{2}} - ε_{3} ϑ (x, t) = ε_{4} \ddot{ϑ} (x, t) - ε_{5} \frac{\partial^{2} \ddot{w} (x, t)}{\partial x^{2}} - ε_{6} q (x, t),

20

σ_{x x} = e - ε_{7} θ,

where:

ε_{1} = \frac{12}{h^{2}}, ε_{2} = \frac{24 β T_{0}}{h π^{2} (λ + 2 μ)}, ε_{3} = p^{2}, ε_{4} = ε c_{0}^{2},

ε_{5} = \frac{c_{0}^{2} β z}{K^{*} s i n (p z)}, ε_{6} = c_{0}, ε_{7} = \frac{β T_{0}}{(λ + 2 μ)} .

(The primes have been dropped for convenience).

Laplace transform will be applied with the following definition:

21

\bar{f} (x, s) = \int_{0}^{\infty} f (x, t) e^{- s t} d t,

where the inverse of the Laplace transform takes the form:

22

L^{- 1} (\bar{f} (s)) = f (t) \approx \frac{e^{υ t}}{t} [\frac{1}{2} \bar{f} (υ) + R e \sum_{n = 1}^{N} {(- 1)}^{n} \bar{f} (υ + \frac{i n π}{t})],

where $R e$ means the real part, while $i$ is the imaginary number unit, for faster convergence, many experiments confirmed that the value of the parameter “ $υ$ ” could satisfy the relation $υ t \approx$ 4.7 [39].

Then, the Eqs. (18)-(20) will take the following forms:

23

\frac{d^{4} \bar{w}}{d x^{4}} + ε_{1} s^{2} \bar{w} + ε_{2} \frac{d^{2} \bar{ϑ}}{d x^{2}} = 0,

24

\frac{d^{2} \bar{ϑ}}{d x^{2}} - ε_{3} \bar{ϑ} = ε_{4} s^{2} \bar{ϑ} - ε_{5} s^{2} \frac{d^{2} w}{\partial x^{2}} - ε_{6} \bar{q},

25

{\bar{σ}}_{x x} = \bar{e} - ε_{7} \bar{θ},

26

\bar{e} = - z \frac{d^{2} \bar{w}}{d x^{2}} .

Consider that the beam is subjected to a particular heating source that comes from the thermal effect due to connection with a simple circuit with electrical resistance $R_{e}$ (Ω) and electric voltage $V$ (V). Then, Joule’s equation of electrical heating is given by:

27

q = \frac{V^{2}}{R_{e}} t .

Then, after using Laplace transform, we have:

28

\bar{q} = \frac{V^{2}}{R_{e} s^{2}},

which gives:

29

\frac{d^{2} \bar{ϑ}}{d x^{2}} - ε_{3} \bar{ϑ} = ε_{4} s^{2} \bar{ϑ} - ε_{5} s^{2} \frac{d^{2} w}{\partial x^{2}} - \frac{ε_{6} V^{2}}{s^{2} R_{e}} .

We re-write the Eqs (23) and (24) obtain the forms:

30

(D^{4} + ε_{1} s^{2}) \bar{w} + ε_{2} D^{2} \bar{ϑ} = 0,

and

31

- ε_{5} s^{2} D^{2} \bar{w} + (D^{2} - (ε_{3} + ε_{4} s^{2})) \bar{ϑ} = - \frac{ε_{6} V^{2}}{s^{2} R_{e}},

where $D^{r} = d^{r} / d x^{r}$ .

By eliminating the Eqs. (30) and (31), we obtain:

32

\{D^{6} - L D^{4} + M D^{2} - N\} \bar{w} = 0,

and

33

\{D^{6} - L D^{4} + M D^{2} - N\} \bar{ϑ} = - ψ,

where $L = ε_{3} + ε_{4} s^{2} - ε_{5} ε_{2} s^{2}$ , $M = ε_{1} s^{2}$ , $N = ε_{1} s^{2} (ε_{3} + ε_{4} s^{2})$ , and $ψ = ε_{1} ε_{6} V^{2} / R_{e}$ .

The general solution of the Eq. (32) as follows:

34

\bar{w} = \sum_{j = 1}^{3} A_{j} s i n h (k_{j} (l - x)) .

The general solution of the Eq. (33) as follows:

35

\bar{ϑ} = \frac{ψ}{N} + \sum_{j = 1}^{3} B_{j} s i n h (k_{j} (l - x)) .

To get the relation between the parameters $A_{j}$ and $B_{j}$ , we use the relation in Eq. (30), which gives:

36

(K_{j}^{4} + ε_{1} s^{2}) A_{j} + ε_{2} K_{j}^{2} B_{j} = 0, j = 1,2, 3 .

Then we have:

37

\bar{ϑ} = \frac{ψ}{N} - \frac{1}{ε_{2}} \sum_{j = 1}^{3} \frac{(K_{j}^{4} + ε_{1} s^{2})}{K_{j}^{2}} A_{j} s i n h (k_{j} (l - x)) .

The boundary conditions:

38

\sum_{j = 1}^{3} A_{j} s i n h (k_{j} l) = 0,

39

\sum_{j = 1}^{3} k_{j}^{2} A_{j} s i n h (k_{j} l) = 0,

40

\sum_{j = 1}^{3} \frac{(K_{j}^{4} + ε_{1} s^{2})}{K_{j}^{2}} A_{j} s i n h (k_{j} l) = \frac{ε_{2} ψ}{N} .

By solving the Eqs. (38)-(40), we get the parameters $A_{1}$ , $A_{2}$ , $A_{3}$ as follows:

A_{1} = \frac{ε_{2} (ε_{3} + ε_{4} s^{2}) ψ}{(k_{1}^{2} - k_{2}^{2}) (k_{1}^{2} - k_{3}^{2}) s i n h (k_{1} l)}, A_{2} = \frac{ε_{2} (ε_{3} + ε_{4} s^{2}) ψ}{(k_{2}^{2} - k_{1}^{2}) (k_{2}^{2} - k_{3}^{2}) s i n h (k_{2} l)},

A_{3} = \frac{ε_{2} (ε_{3} + ε_{4} s^{2}) ψ}{(k_{3}^{2} - k_{1}^{2}) (k_{3}^{2} - k_{2}^{2}) s i n h (k_{3} l)} .

That completes the solution of the Laplace transform domain.

The lateral deflection function is as follows:

41

\bar{w} (x, s) = ε_{2} (ε_{3} + ε_{4} s^{2}) ψ [\frac{s i n h (k_{1} (l - x))}{(k_{1}^{2} - k_{2}^{2}) (k_{1}^{2} - k_{3}^{2}) s i n h (k_{1} l)}

+ \frac{s i n h (k_{2} (l - x))}{(k_{2}^{2} - k_{1}^{2}) (k_{2}^{2} - k_{3}^{2}) s i n h (k_{2} l)} + \frac{s i n h (k_{3} (l - x))}{(k_{3}^{2} - k_{1}^{2}) (k_{3}^{2} - k_{2}^{2}) s i n h (k_{3} l)}],

and the temperature increment function is as follows:

42

\bar{θ} (x, s) = \frac{ψ s i n (p z)}{ε_{1} s^{2} (ε_{3} + ε_{4} s^{2})} - (ε_{3} + ε_{4} s^{2}) ψ s i n (p z) [\frac{(K_{1}^{4} + ε_{1} s^{2}) s i n h (k_{1} (l - x))}{K_{1}^{2} (k_{1}^{2} - k_{2}^{2}) (k_{1}^{2} - k_{3}^{2}) s i n h (k_{1} l)}

+ \frac{(K_{2}^{4} + ε_{1} s^{2}) s i n h (k_{2} (l - x))}{K_{2}^{2} (k_{2}^{2} - k_{1}^{2}) (k_{2}^{2} - k_{3}^{2}) s i n h (k_{2} l)} + \frac{(K_{3}^{4} + ε_{1} s^{2}) s i n h (k_{3} (l - x))}{K_{3}^{2} (k_{3}^{2} - k_{1}^{2}) (k_{3}^{2} - k_{2}^{2}) s i n h (k_{3} l)}] .

From Eqs. (26) and (41), we obtain the deformation in the form:

43

e (x, z, s) = - z ε_{2} (ε_{3} + ε_{4} s^{2}) ψ [\frac{k_{1}^{2} s i n h (k_{1} (l - x))}{(k_{1}^{2} - k_{2}^{2}) (k_{1}^{2} - k_{3}^{2}) s i n h (k_{1} l)}

+ \frac{k_{2}^{2} s i n h (k_{2} (l - x))}{(k_{2}^{2} - k_{1}^{2}) (k_{2}^{2} - k_{3}^{2}) s i n h (k_{2} l)} + \frac{k_{3}^{2} s i n h (k_{3} (l - x))}{(k_{3}^{2} - k_{1}^{2}) (k_{3}^{2} - k_{2}^{2}) s i n h (k_{3} l)}] .

The strain-energy density function through the nanobeam is given by [40]:

44

ϖ (x, z, t) = \sum_{i, j}^{3} \frac{1}{2} σ_{i j} (x, z, t) e_{i j} (x, z, t) = \frac{1}{2} σ (x, z, t) e (x, z, t) .

3. Numerical results

Copper is taken as the thermoelastic material, so the following values of the different physical constants have been used [32]: $α_{T} =$ 1.78 10^-5 K^-1, $ρ =$ 8954 kg m^-3, $T_{0} =$ 300 K, $C_{υ} =$ 383.1 J kg^-1 K^-1, $λ =$ 77.6×10⁹ N m^-2, $μ =$ 38.6×10⁹ N m^-2.

The resistivity of the graphene in the nanoscale has values $R_{e} =$ 500 Ω [35].

The aspect ratios of the nanobeam are fixed as $l / h =$ 8 and $b = h / 2$ . We will take the range of the nanobeam length $l (1 - 100)$ ×10^-12 m, and the original time $t$ , and the relaxation time $τ_{0}$ of order 10^-12sec and 10^-14sec, respectively.

The figures were prepared by using the dimensionless variables for nanobeam length $l =$ 1.0, $θ_{0} =$ 1.0, $z = h / 4$ , and $t =$ 1.0.

The numerical results of the problem have been illustrated in two groups of figures; the first group shows the distributions of the vibration (lateral deflection), cubical deformation, temperature increment, stress, and strain-energy density when the value of the electrical resistance of the nano-strip of graphene is constant and takes the value $R_{e} =$ 500 Ω and for three different values of the electrical voltage $V =$ (1.0, 1.1, 1.2) V, while the second group represents the distributions of the same functions when the value of the electrical voltage of nano-strip of graphene is constant and takes the value $V =$ 1.0 V and for three different values of the electrical resistance $R_{e} =$ (500, 550, 600) Ω.

Figs. 2-6 show that the value of the electrical voltage has considerable impacts on the distributions of the temperature increment, vibration (lateral deflection), cubical deformation, stress, and strain energy density. The increase in the value of the electrical voltage leads to an increase in the temperature increment and the absolute values of the vibration (lateral deflection), cubical deformation, stress, and strain energy density.

Fig. 2The temperature increment distribution with variance voltage and constant resistance

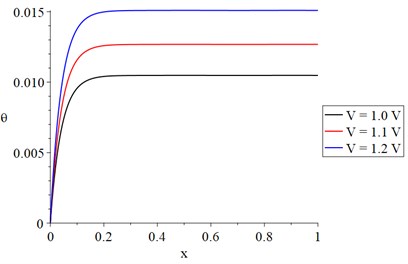
Fig. 3The vibration distribution with variance voltage and constant resistance

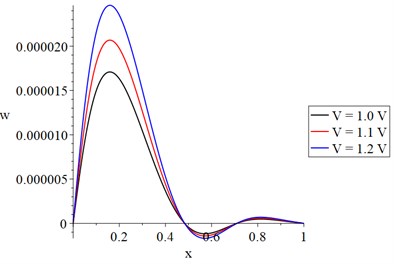
Fig. 4The strain distribution with variance voltage and constant resistance

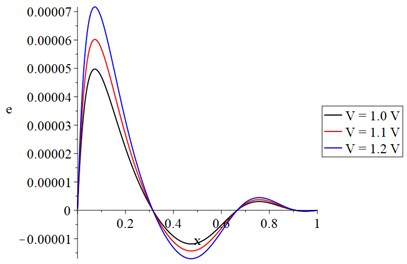
Fig. 5The stress distribution with variance voltage and constant resistance

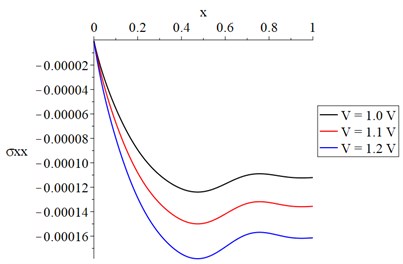
Fig. 6The strain-energy density distribution with variance voltage and constant resistance

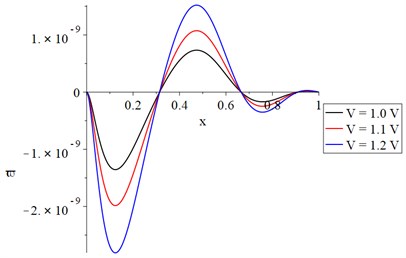
Fig. 7The temperature increment distribution with variance resistance and constant voltage

In Fig. 2, in the three curves, we find that the value of the temperature increment increases sharply up in a distance of not more than 0.15 due to the thermo-electrical effect at this end and then the curves go to the state of stability to the end but with different values based on the voltage value. In Figs. 3, 4 and 6, each curve has three peak points where the absolute value of the peak point increases when the value of the voltage increases. Along the $x$ -axis, the values of the peak points decrease when the distance $x$ increases. In Fig. 5, each curve of the stress curves has two peak points, and its absolute value increases when the voltage value increases.

Fig. 8The vibration distribution with variance resistance and constant voltage

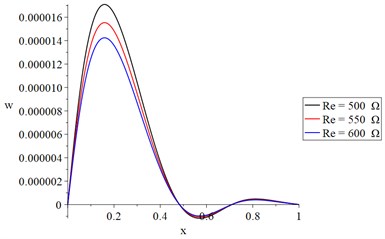
Fig. 9The strain distribution with variance resistance and constant voltage

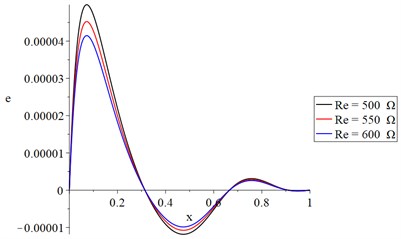
Fig. 10The stress distribution with variance resistance and constant voltage

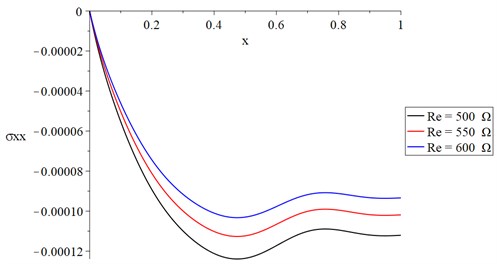
Fig. 11The strain-energy density distribution with variance resistance and constant voltage

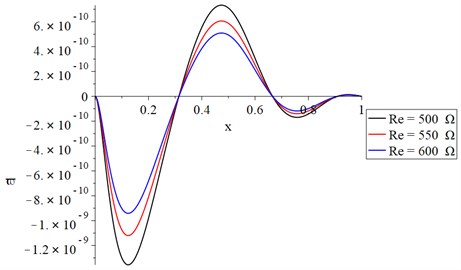
The distributions of temperature increment, vibration (lateral deflection), cubical deformation, stress, and strain energy density are all significantly affected by the electrical resistance value, as shown in Figs. 7-11. The temperature increment and absolute values of the vibration (lateral deflection), cubical deformation, stress, and strain energy density decrease with an increase in the electrical resistance.

In Fig. 7, we find that the value of temperature increment increases sharply up in a distance of not more than 0.15 due to the thermo-electrical effect at this end and then the curves go to the state of stability to the end but with different values based on the electrical resistance value. In Figs. 8, 9, and 11, each curve has three peak points where the value of each peak point decreases when the value of the electrical resistance increases. Along the $x$ -axis, the values of the peak points decrease when the distance $x$ increases. In Fig. 10, each curve of the stress curves has two peak points, and its absolute value decreases when the electrical resistance increases.

As a result, we can claim that the electrical resistance may be utilized to control both the vibration and the energy generated along the microbeam.

To ensure that the findings are reliable, we compared them to those reported in [36, 37].

4. Conclusions

Green-Naghdi type-II heat conduction model has been applied to analyze thermoelastic microbeams in this study. The nano-strip of graphene at the microbeam’s beginning end is connected by a low-voltage electrical current. The extended thermoelasticity theory Lord-Shulman model was used. The microbeam has been thermally loaded because of the electrical current operating on a low-voltage nano-strip of graphene.

Electrical voltage and electrical resistance have been discovered to play a substantial role in all the functions tested.

Gradually increasing electrical voltage raises thermal and mechanical stress and strain energy density as well as the lateral deflection, stress and strain energy density values. Temperature increment, absolute values of vibration (lateral deflection), cubical deformation, tension, and strain energy density increase with increasing electrical resistance.

The graphene microstrip might be used as a tuner to regulate the vibration and energy of the microbeam by controlling the voltage and resistance of the microstrip.

References

N. Alghamdi, “Dual-phase-lagging thermoelastic damping vibration in micro-nano scale beam resonators with voids,” International Journal of Multidisciplinary and Current Research, Vol. 5, pp. 71–78, 2017.

Search CrossRef
N. A. Alghamdi and H. M. Youssef, “Dual-phase-lagging thermoelastic damping in-extensional vibration of rotating nano-ring,” Microsystem Technologies, Vol. 23, No. 10, pp. 4333–4343, Oct. 2017, https://doi.org/10.1007/s00542-017-3294-z

Publisher
M. A. Biot, “Thermoelasticity and irreversible thermodynamics,” Journal of Applied Physics, Vol. 27, No. 3, pp. 240–253, 1956.

Publisher
H. M. Youssef and N. Alghamdi, “Thermoelastic damping in nanomechanical resonators based on two-temperature generalized thermoelasticity theory,” Journal of Thermal Stresses, Vol. 38, No. 12, pp. 1345–1359, 2015.

Publisher
H. W. Lord and Y. Shulman, “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, pp. 299–309, Sep. 1967, https://doi.org/10.1016/0022-5096(67)90024-5

Publisher
R. S. Dhaliwal and H. H. Sherief, “Generalized thermoelasticity for anisotropic media,” Quarterly of Applied Mathematics, Vol. 38, No. 1, pp. 1–8, 1980.

Publisher
C. M. Hoang, “Thermoelastic damping depending on vibration modes of nano beam resonator,” Communications in Physics, Vol. 25, No. 4, p. 317, Jan. 2016, https://doi.org/10.15625/0868-3166/25/4/6887

Publisher
A. K. Naik, M. S. Hanay, W. K. Hiebert, X. L. Feng, and M. L. Roukes, “Towards single-molecule nanomechanical mass spectrometry,” Nature Nanotechnology, Vol. 4, No. 7, pp. 445–450, Jul. 2009, https://doi.org/10.1038/nnano.2009.152

Publisher
A. D. O. ’Connell et al., “Quantum ground state and single-phonon control of a mechanical resonator,” Nature, Vol. 464, No. 7289, pp. 697–703, Apr. 2010, https://doi.org/10.1038/nature08967

Publisher
J. T. M. van Beek and R. Puers, “A review of MEMS oscillators for frequency reference and timing applications,” Journal of Micromechanics and Microengineering, Vol. 22, No. 1, p. 013001, Jan. 2012, https://doi.org/10.1088/0960-1317/22/1/013001

Publisher
I. A. Abbas, “Analytical solution for a free vibration of a thermoelastic hollow sphere,” Mechanics Based Design of Structures and Machines, Vol. 43, No. 3, pp. 265–276, Jul. 2015, https://doi.org/10.1080/15397734.2014.956244

Publisher
N. Sarkar and A. Lahiri, “A three-dimensional thermoelastic problem for a half-space without energy dissipation,” International Journal of Engineering Science, Vol. 51, pp. 310–325, Feb. 2012, https://doi.org/10.1016/j.ijengsci.2011.08.005

Publisher
M. Rezazadeh, M. Tahani, and S. M. Hosseini, “Thermoelastic damping in a nonlocal nano-beam resonator as NEMS based on the type III of Green-Naghdi theory (with energy dissipation),” International Journal of Mechanical Sciences, Vol. 92, pp. 304–311, Mar. 2015, https://doi.org/10.1016/j.ijmecsci.2015.01.001

Publisher
S. Y. Atwa, “Generalized magneto-thermoelasticity with two temperature and initial stress under Green-Naghdi theory,” Applied Mathematical Modelling, Vol. 38, No. 21-22, pp. 5217–5230, Nov. 2014, https://doi.org/10.1016/j.apm.2014.04.023

Publisher
M. I. A. Othman, S. Y. Atwa, and R. M. Farouk, “The effect of diffusion on two-dimensional problem of generalized thermoelasticity with Green-Naghdi theory,” International Communications in Heat and Mass Transfer, Vol. 36, No. 8, pp. 857–864, Oct. 2009, https://doi.org/10.1016/j.icheatmasstransfer.2009.04.014

Publisher
Saurav Sharma, Kunal Sharma, and Raj Rani Bhargava, “Effect of viscosity on wave propagation in anisotropic thermoelastic with Green-Naghdi theory type-II and type-III,” Физика и Механика Материалов, Vol. 27, No. 2, pp. 144–158, 2013.

Search CrossRef
I. A. Abbas, “Fractional order GN model on thermoelastic interaction in an infinite fibre-reinforced anisotropic plate containing a circular hole,” Journal of Computational and Theoretical Nanoscience, Vol. 11, No. 2, pp. 380–384, Feb. 2014, https://doi.org/10.1166/jctn.2014.3363

Publisher
J. N. Sharma and D. Grover, “Thermoelastic vibrations in micro-/nano-scale beam resonators with voids,” Journal of Sound and Vibration, Vol. 330, No. 12, pp. 2964–2977, Jun. 2011, https://doi.org/10.1016/j.jsv.2011.01.012

Publisher
Y. Sun and M. Saka, “Thermoelastic damping in micro-scale circular plate resonators,” Journal of Sound and Vibration, Vol. 329, No. 3, pp. 328–337, Feb. 2010, https://doi.org/10.1016/j.jsv.2009.09.014

Publisher
N. S. Al-Huniti, M. A. Al-Nimr, and M. Naji, “Dynamic response of a rod due to a moving heat source under the hyperbolic heat conduction model,” Journal of Sound and Vibration, Vol. 242, No. 4, pp. 629–640, May 2001, https://doi.org/10.1006/jsvi.2000.3383

Publisher
E. A. N. Al-Lehaibi and H. M. Youssef, “Vibration of gold nano-beam with variable Young’s modulus Due to Thermal Shock,” World Journal of Nano Science and Engineering, Vol. 5, No. 4, pp. 194–203, 2015, https://doi.org/10.4236/wjnse.2015.54020

Publisher
B. A. Boley, “Approximate analyses of thermally induced vibrations of beams and plates,” Journal of Applied Mechanics, Vol. 39, No. 1, pp. 212–216, Mar. 1972, https://doi.org/10.1115/1.3422615

Publisher
J. Kidawa-Kukla, “Application of the Green functions to the problem of the thermally induced vibration of a beam,” Journal of Sound and Vibration, Vol. 262, No. 4, pp. 865–876, May 2003, https://doi.org/10.1016/s0022-460x(02)01133-1

Publisher
G. D. Manolis and D. E. Beskos, “Thermally induced vibrations of beam structures,” Computer Methods in Applied Mechanics and Engineering, Vol. 21, No. 3, pp. 337–355, Mar. 1980, https://doi.org/10.1016/0045-7825(80)90101-2

Publisher
M. Biot, “Theory of stress‐strain relations in anisotropic viscoelasticity and relaxation phenomena,” Journal of Applied Physics, Vol. 25, No. 11, pp. 1385–1391, 1954.

Publisher
M. A. Biot, “Variational principles in irreversible thermodynamics with application to viscoelasticity,” Physical Review, Vol. 97, No. 6, pp. 1463–1469, Mar. 1955, https://doi.org/10.1103/physrev.97.1463

Publisher
A. D. Drozdov, “A constitutive model in finite thermoviscoelasticity based on the concept of transient networks,” Acta Mechanica, Vol. 133, No. 1-4, pp. 13–37, Mar. 1999, https://doi.org/10.1007/bf01179008

Publisher
M. A. Ezzat and A. S. El-Karamany, “The relaxation effects of the volume properties of viscoelastic material in generalized thermoelasticity,” International Journal of Engineering Science, Vol. 41, No. 19, pp. 2281–2298, Nov. 2003, https://doi.org/10.1016/s0020-7225(03)00108-3

Publisher
J. M. Carcione, F. Poletto, and D. Gei, “3-D wave simulation in anelastic media using the Kelvin-Voigt constitutive equation,” Journal of Computational Physics, Vol. 196, No. 1, pp. 282–297, May 2004, https://doi.org/10.1016/j.jcp.2003.10.024

Publisher
D. Grover, “Viscothermoelastic vibrations in micro-scale beam resonators with linearly varying thickness,” Canadian Journal of Physics, Vol. 90, No. 5, pp. 487–496, May 2012, https://doi.org/10.1139/p2012-044

Publisher
D. Grover, “Damping in thin circular viscothermoelastic plate resonators,” Canadian Journal of Physics, Vol. 93, No. 12, pp. 1597–1605, Dec. 2015, https://doi.org/10.1139/cjp-2014-0575

Publisher
D. Grover, “Transverse vibrations in micro-scale viscothermoelastic beam resonators,” Archive of Applied Mechanics, Vol. 83, No. 2, pp. 303–314, Feb. 2013, https://doi.org/10.1007/s00419-012-0656-y

Publisher
D. Grover and R. K. Seth, “Viscothermoelastic micro-scale beam resonators based on dual-phase lagging model,” Microsystem Technologies, Vol. 24, No. 3, pp. 1667–1672, Mar. 2018, https://doi.org/10.1007/s00542-017-3515-5

Publisher
K. S. Novoselov et al., “Electric field effect in atomically thin carbon films,” Science, Vol. 306, No. 5696, pp. 666–669, Oct. 2004, https://doi.org/10.1126/science.1102896

Publisher
P. N. Nirmalraj, T. Lutz, S. Kumar, G. S. Duesberg, and J. J. Boland, “Nanoscale mapping of electrical resistivity and connectivity in graphene strips and networks,” Nano Letters, Vol. 11, No. 1, pp. 16–22, Jan. 2011, https://doi.org/10.1021/nl101469d

Publisher
K. Saanouni, J. F. Mariage, A. Cherouat, and P. Lestriez, “Numerical prediction of discontinuous central bursting in axisymmetric forward extrusion by continuum damage mechanics,” Computers and Structures, Vol. 82, No. 27, pp. 2309–2332, Oct. 2004, https://doi.org/10.1016/j.compstruc.2004.05.018

Publisher
D. Grover and R. K. Seth, “Generalized viscothermoelasticity theory of dual-phase-lagging model for damping analysis in circular micro-plate resonators,” Mechanics of Time-Dependent Materials, Vol. 23, No. 1, pp. 119–132, Feb. 2019, https://doi.org/10.1007/s11043-018-9388-x

Publisher
Hamdy Youssef and Najat A. Al-Ghamdi, “Vibration of Gold nano beam in context of two-temperature generalized thermoelasticity without energy dissipation,” ICTEA: International Conference on Thermal Engineering, Vol. 2017, Mar. 2017.

Search CrossRef
D. Tzou and M.-T. M. H. Transfer, The Lagging Behavior. Washington: Taylor Francis, 1997.

Search CrossRef
H. M. Youssef and K. A. Elsibai, “State-space approach to vibration of gold nano-beam induced by ramp type heating,” Nano-Micro Letters, Vol. 2, No. 3, pp. 139–147, Sep. 2010, https://doi.org/10.1007/bf03353632

Publisher

Cited by

Stability and analysis of the vibrating motion of a four degrees-of-freedom dynamical system near resonance

TS Amer | AI Ismail | MO Shaker | WS Amer | HA Dahab

(2024)

Thermo-Electrical Influence of Graphene Nano-Strip on Viscothermoelastic Nanobeam Vibration

Mohammad Salem J. Alzahrani | Najat A. Alghamdi | Hajar A. Alshehri

(2023)

Evaluation of the stability of a two degrees-of-freedom dynamical system

TS Amer | AI Ismail | WS Amer

(2023)

Influence of the static pre-stress on the thermal quality factor of a micro-resonator under the dual-phase-lag heat conduction model

Eman A. N. Al-Lehaibi

(2023)

Influence of graphene nano-strips on the vibration of thermoelastic nanobeams

Mohammad Salem J. Alzahrani | Najat A. Alghamdi | Jamiel A. Alotaibi

(2023)

About this article

Received

03 April 2022

Accepted

31 May 2022

Published

30 June 2022

DOI

https://doi.org/10.21595/jets.2022.22568

Keywords

vibration

thermoelasticity

nanobeam

thermo-electrical effect

graphene

electrical voltage

electrical resistivity

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2022 05 15

The vibration analysis of a nanobeam due to a ramp-type heating under Moore-Gibson-Thompson theory of thermoelasticity

Eman A. N. Al-Lehaibi

Research article

2021 11 11

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir, Adiya Dar, Mohamed I. A. Othman

Research article

2021 06 30

Vibration of a simply supported graphene sheet with uncertain small scale parameter based on nonlocal theory

G. Q. Xie, S. S. Ni

Research article

2020 11 21

Numerical analysis of the damage mechanics variable and vibration of a viscothermoelastic microbeam with variable thermal conductivity

Hamdy M. Youssef, Alaa A. El-Bary, Haitham M. Atef, A. H. El-Sharif

H. M. Youssef and A. A. Al Thobaiti, “The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model,” Journal of Engineering and Thermal Sciences, Vol. 2, No. 1, pp. 1–12, Jun. 2022, https://doi.org/10.21595/jets.2022.22568

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2022.22568
UR  - https://doi.org/10.21595/jets.2022.22568
TI  - The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model
T2  - Journal of Engineering and Thermal Sciences
AU  - Youssef, Hamdy M.
AU  - Al Thobaiti, Abdullah A.
PY  - 2022
DA  - 2022/06/30
PB  - JVE International Ltd.
SP  - 1-12
VL  - 2
IS  - 1
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Youssef_2022,
	doi = {10.21595/jets.2022.22568},
	url = {https://doi.org/10.21595/jets.2022.22568},
	year = 2022,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {2},
	number = {1},
	pages = {1--12},
	author = {Hamdy M. Youssef and Abdullah A. Al Thobaiti},
	title = {The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-{II} model},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]H. M. Youssef and A. A. Al Thobaiti, “The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model,” Journal of Engineering and Thermal Sciences, vol. 2, no. 1, pp. 1–12, Jun. 2022, doi: 10.21595/jets.2022.22568.

Copy IEEE

Copied to clipboard!

Youssef, Hamdy M., and Abdullah A. Al Thobaiti. “The Vibration of a Thermoelastic Nanobeam Due to Thermo-Electrical Effect of Graphene Nano-Strip under Green-Naghdi Type-II Model.” Journal of Engineering and Thermal Sciences 2, no. 1 (June 30, 2022): 1–12. https://doi.org/10.21595/jets.2022.22568.

Copy Chicago

Copied to clipboard!

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Abstract

Highlights

1. Introduction

2. Problem formulation

3. Numerical results

4. Conclusions

References

Cited by

About this article

Related Articles