Dual-phase-lag model on microelongated thermoelastic rotating medium

Othman, Mohamed I. A.; Atwa, Sarhan Y.; Eraki, E. E. M.; Ismail, Mohamed F.

doi:10.21595/jets.2022.22597

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 30 June 2022

Check for updates

Dual-phase-lag model on microelongated thermoelastic rotating medium

Mohamed I. A. Othman¹

Sarhan Y. Atwa²

E. E. M. Eraki³

Mohamed F. Ismail⁴

^{1, 3}Department of Mathematics, Faculty of Science, Zagazig University, P.O. Box 44519, Zagazig, Egypt

^{2, 4}Department of Engineering Mathematics and Physics, Higher Institute of Engineering, El Shorouk Academy, P.O. Box 11837, Cairo, Egypt

Corresponding Author:

Mohamed I. A. Othman

Cite the article Download PDF

Downloads 321

CrossRef Citations 1

Abstract

The dual-phase-lag (DPL) model is applied to study the influence of rotation on a two-dimensional micro-elongated thermoelastic medium problem. Mechanical force along with the layer of the elastic half-space interface and micro-elongated thermoelastic half-space is applied. The analytic expressions for displacement component, temperature distribution, micro-elongational scalar and stress components have been derived and represented graphically. The rotation has been studied in the presence DPL model and Lord-Shulman theory.

1. Introduction

A microelongated elastic solid possesses four degrees of freedom: three for translation and micro-elongation. In micro-elongation theory, the material particles can perform only volumetric micro-elongation in addition to classical deformation of the medium. The material points of such a medium can stretch and contract independently of their translations. Solid-liquid crystals, composite materials reinforced with chopped elastic fibres porous media with pores filled with non-viscous fluid or gas can be categorized as micro-elongated medium. The variation of periodical heat source response in a functionally graded micro-elongated medium was discussed by [1, 2]. The plane strain problem in a thermoelastic micro-elongated solid with an overlying infinite non-viscous fluid was discussed by [3]. More interesting problems have been studied about the thermoelastic micro-elongated solid in different cases [4-9].

In the generalized theories, the governing equations involve thermal relaxation times and they are of a hyperbolic type. The extended thermoelasticity theory by [10-14] which introduces one relaxation time in the thermoelastic process and the temperature-rate dependent theory of thermoelasticity by [15], which takes into account two relaxation times are two well-established generalized theories of thermoelasticity.

A new model called the dual-phase-lag model for the heat transport mechanism in which Fourier’s law is replaced by an approximation to the modification of Fourier’s law with two different time translations for the heat flux and the temperature gradient was investigated by [16-20]. The effect of thermal loading due to laser pulse in generalized thermoelastic medium with voids in the dual-phase-lag model was studied by [21]. A dynamic problem in thermoelastic solid using a dual-phase-lag model with an internal heat source was explained by [22]. The effect of rotation on micropolar generalized thermoelasticity with two-temperatures and the thermal laser pulse using a DPL model has been discussed by [23, 24].

In this paper, the effect of rotation on a two-dimensional micro-elongated thermoelastic medium problem has been discussed. The normal mode analysis is used to derive the expressions for the considered variables for a DPL model of thermoelasticity and the variances of the considered variables are represented graphically.

2. Formulation of the problem

The system of prevailing equations of a microelongated thermoelastic solid with rotation, in the DPL model, as [4, 7] (Fig. 1):

1

σ_{i j, j} = ρ [u_{i, t t} + {Ω \times (Ω \times u)}_{i} + (2 Ω \times u_{, t})_{i}],

2

a_{0} φ_{, i i} + β_{1} T - λ_{1} φ - λ_{0} u_{j, j} = \frac{1}{2} ρ j_{0} φ_{, t t},

3

k (1 + τ_{θ} \frac{\partial}{\partial t}) T_{, i i} = (1 + τ_{q} \frac{\partial}{\partial t}) (ρ c_{e} \frac{\partial T}{\partial t} + β_{0} T u_{k, k t}) + β_{1} T_{0} φ_{, t},

4

σ_{i j} = 2 μ ε_{i j} + (λ e - β_{0} T + λ_{0} φ) δ_{i j} .

where the displacement vector $u (x, z, t) = u (u_{1}, 0, u_{3})$ , and the rotation $Ω = (0, Ω, 0)$ then the equations of motion are given by:

5

μ \nabla^{2} u_{1} + (λ + μ) e_{, x} - β_{0} T_{, x} + λ_{0} φ_{, x} = ρ (u_{1, t t} - Ω^{2} u_{1} + 2 Ω u_{3, t}),

6

μ \nabla^{2} u_{3} + (λ + μ) e_{, z} - β_{0} T_{, z} + λ_{0} φ_{, z} = ρ (u_{3, t t} - Ω^{2} u_{3} + 2 Ω u_{1, t}) .

For simplification, we shall use the following non-dimensional variables:

7

{x'}_{i} = \frac{w^{*}}{c_{1}} x_{i}, z^{'} = \frac{w^{*}}{c_{1}} z, {u'}_{i} = \frac{w^{*} ρ c_{1}}{β_{0} T_{0}} u_{i}, u_{i}^{e'} = \frac{w^{*} ρ c_{1}}{β_{0} T_{0}} u_{i}^{e},

t^{'} = w^{*} t, {τ^{'}}_{θ} = w^{*} τ_{θ}, {τ^{'}}_{q} = w^{*} τ_{q}, {σ'}_{i j} = \frac{σ_{i j}}{β_{0} T_{0}}, σ_{i j}^{e'} = \frac{σ_{i j}^{e}}{β_{0} T_{0}},

φ^{'} = \frac{λ_{0}}{β_{0} T_{0}} φ, T^{'} = \frac{T}{T_{0}}, Ω^{'} = \frac{Ω}{w^{*}}, {P^{'}}_{1} = \frac{P_{1}}{β_{0} T_{0}}, w^{*} = \frac{ρ c_{1}^{2} c_{e}}{k}, c_{1}^{2} = \frac{λ + 2 μ}{ρ} .

Fig. 1Geometry of the problem

The displacement potentials $Φ (x, z, t)$ and $Ψ (x, z, t)$ which relate to displacement components have been introduced, we obtain:

8

u_{1} = Φ_{, x} + ψ_{, z}, u_{3} = Φ_{, z} - ψ_{, x} .

From Eqs. (7) and (8) into Eqs. (2), (3), (5) and (6), we obtain:

9

[(a_{1} + a_{2}) \nabla^{2} + Ω^{2} - \frac{\partial^{2}}{\partial t^{2}}] Φ + 2 Ω ψ_{, t} - T + φ = 0,

10

- 2 Ω Φ_{, t} + (a_{1} \nabla^{2} + Ω^{2} - \frac{\partial^{2}}{\partial t^{2}}) ψ = 0,

11

- a_{5} \nabla^{2} Φ + a_{3} T + (\nabla^{2} - a_{4} - a_{6} \frac{\partial^{2}}{\partial t^{2}}) φ = 0,

12

- a_{8} (1 + τ_{q} \frac{\partial}{\partial t}) \nabla^{2} Φ_{, t} + (1 + τ_{θ} \frac{\partial}{\partial t}) \nabla^{2} T - a_{7} (1 + τ_{q} \frac{\partial}{\partial t}) T_{, t} - a_{9} φ = 0 .

3. Normal mode analysis

The solution of the considered physical variable can be decomposed in terms of normal modes as the following form:

13

[u_{i}, φ, T, ψ, Φ, σ_{i j}, u_{i}^{e}, σ_{i j}^{e}] (x, z, t) = [u_{i}^{*}, φ^{*}, T^{*}, ψ^{*}, Φ^{*}, σ_{i j}^{*}, u_{i}^{e *}, σ_{i j}^{e *}] (z) e^{(ω t + i b x)},

where, $ω$ is a complex constant, $i = \sqrt{- 1}$ , $b$ is the wave number in the $x$ direction.

Using Eq. (13) into Eqs. (9)-(12), then we have:

14

(a_{10} D^{2} + a_{11}) Φ^{*} + 2 Ω ω ψ^{*} - T^{*} + φ^{*} = 0,

15

- 2 Ω ω Φ^{*} + (a_{1} D^{2} + a_{12}) ψ^{*} = 0,

16

(- a_{5} D^{2} + a_{13}) Φ^{*} + a_{3} T^{*} + (D^{2} - a_{14}) φ^{*} = 0,

17

(- a_{17} D^{2} + a_{18}) Φ^{*} + (a_{16} D^{2} - a_{19}) T^{*} - a_{9} w φ^{*} = 0 .

Eqs. (14-17) have a non-trivial solution if the determinant coefficients of the physical quantities equal to zero, then we get:

18

(D^{8} - A D^{6} + B D^{4} - C D^{2} + E) {Φ^{*} (z), ψ^{*} (z), T^{*} (z), φ^{*} (z)} = 0 .

The coefficients $a_{i}$ , $A$ , $B$ , $C$ , $E$ and $H_{i n}$ are given in Appendix A1.

Eq. (18) can be factorized as:

19

(D^{2} - k_{1}^{2}) (D^{2} - k_{2}^{2}) (D^{2} - k_{3}^{2}) (D^{2} - k_{4}^{2}) {Φ^{*} (z), ψ^{*} (z), T^{*} (z), φ^{*} (z)} = 0,

where, $k_{n}^{2}$ , ( $n =$ 1, 2, 3, 4) are roots of the characteristic equation of Eq. (19).

The general solutions of Eq. (19) bound as $(z \to \infty)$ is given by:

20

(Φ^{*}, ψ^{*}, T^{*}, φ^{*}) (z) = \sum_{n = 1}^{4} (1, H_{1 n}, H_{2 n}, H_{3 n}) M_{n} e^{- k_{n} z} .

Substituting from Eq. (20) into Eq. (8) we obtain the components of displacements:

21

u_{1}^{*} (z) = \sum_{n = 1}^{4} (i b - k_{n} H_{1 n}) M_{n} e^{- k_{n} z},

22

u_{3}^{*} (z) = \sum_{n = 1}^{4} - (k_{n} + i b H_{1 n}) M_{n} e^{- k_{n} z} .

Substituting Eqs. (7) and (13) into (4) and by using of Eqs. (20)-(22) we get:

23

(σ_{x x}^{*}, σ_{z z}^{*}, σ_{x z}^{*}) (z) = \sum_{n = 1}^{4} (H_{4 n}, H_{5 n}, H_{6 n}) M_{n} e^{- k_{n} z} .

The equations of motion and stress components in an elastic medium are given by [7]:

24

σ_{i j, j}^{e} = ρ^{e} u_{i, t t}^{e},

25

σ_{i j}^{e} = λ^{e} u_{k, k}^{e} δ_{i j} + μ^{e} (u_{i, j}^{e} + u_{j, i}^{e}) .

Substituting from Eqs. (7) and (13) into Eq. (24):

26

(l_{3} D^{2} - δ_{1}) u_{1}^{e *} + i b l_{2} D u_{3}^{e *} = 0,

27

i b l_{2} D u_{1}^{e *} + (l_{1} D^{2} - δ_{2}) u_{3}^{e *} = 0 .

Eliminating $u_{1}^{e *}$ , $u_{3}^{e *}$ between Eqs. (26) and (27), we obtain:

28

(D^{4} - G D^{2} + N) {u_{1}^{e *} (z), u_{3}^{e *} (z)} = 0 .

Eq. (28) can be factorized as:

29

(D^{2} - r_{1}^{2}) (D^{2} - r_{2}^{2}) {u_{1}^{e *} (z), u_{3}^{e *} (z)} = 0,

where, $r_{n}^{2}$ , ( $n =$ 1, 2) are the roots of the characteristic equation of Eq. (29), the solutions of Eq. (29) are:

30

u_{1}^{e *} (z) = \sum_{n = 1}^{2} R_{n} e^{- r_{n} z} + \sum_{n = 1}^{2} R_{n + 2} e^{r_{n} z},

31

u_{3}^{e *} (z) = \sum_{n = 1}^{2} L_{1 n} R_{n} e^{- r_{n} z} + \sum_{n = 1}^{2} L_{1 (n + 2)} R_{n + 2} e^{r_{n} z} .

From Eqs. (7) and (13) into (25) and by using the Eqs. (30) and (31), we obtain the components of stresses in an elastic medium:

32

σ_{x x}^{e *} (z) = \sum_{n = 1}^{2} L_{2 n} R_{n} e^{- r_{n} z} + \sum_{n = 1}^{2} L_{2 (n + 2)} R_{n + 2} e^{r_{n} z},

33

σ_{z z}^{e *} (z) = \sum_{n = 1}^{2} L_{3 n} R_{n} e^{- r_{n} z} + \sum_{n = 1}^{2} L_{2 (n + 2)} R_{n + 2} e^{r_{n} z},

34

σ_{x z}^{e *} (z) = \sum_{n = 1}^{2} L_{4 n} R_{n} e^{- r_{n} z} + \sum_{n = 1}^{2} L_{4 (n + 2)} R_{n + 2} e^{r_{n} z},

where, the coefficients $l_{i}$ , $δ_{i}$ , $G$ , $N$ and $L_{i n}$ are given in Appendix A2

4. The boundary conditions

The parameters $M_{n}$ , ( $n =$ 1, 2, 3, 4) and $R_{n}$ , ( $n =$ 1, 2, 3, 4) can be determined by using the boundary conditions at the surface are [3-7]:

35

σ_{z z} = σ_{z z}^{e}, σ_{x z} = σ_{x z}^{e}, u_{1} = u_{1}^{e}, u_{3} = u_{3}^{e}, φ = 0, \frac{\partial T}{\partial z} = 0, a t z = 0,

σ_{z z} = σ_{z z}^{e} - P_{1} e^{(ω t + i b x)}, σ_{x z} = 0, a t z = - h,

where, $P_{1}$ is the magnitude of the mechanical force.

The using of the expressions of the variables considered in the past boundary conditions Eq. (35), to get the equations that are satisfied with the parameters. And hence, eight equations will be gained. The inverse matrix method is applied to the eighth equation, to obtain the value of $M_{n}$ ( $n =$ 1, 2, 3, 4) and $R_{n}$ ( $n =$ 1, 2, 3, 4):

36

(\begin{array}{l} M_{1} \\ M_{2} \\ M_{3} \\ M_{4} \\ R_{1} \\ R_{2} \\ R_{3} \\ R_{4} \end{array}) = {(\begin{matrix} H_{51} & H_{52} & H_{53} & H_{54} & - L_{31} & - L_{32} & - L_{33} & - L_{34} \\ H_{61} & H_{62} & H_{63} & H_{64} & - L_{41} & - L_{42} & - L_{43} & - L_{44} \\ i b - k_{1} H_{11} & i b - k_{2} H_{12} & i b - k_{3} H_{13} & i b - k_{4} H_{14} & - 1 & - 1 & - 1 & - 1 \\ - k_{1} - i b H_{11} & - k_{2} - i b H_{12} & - k_{3} - i b H_{13} & - k_{4} - i b H_{14} & - L_{11} & - L_{12} & - L_{13} & - L_{14} \\ H_{31} & H_{32} & H_{33} & H_{34} & 0 & 0 & 0 & 0 \\ - k_{1} H_{21} & - k_{2} H_{22} & - k_{3} H_{23} & - k_{4} H_{24} & 0 & 0 & 0 & 0 \\ H_{51} e^{k_{1} h} & H_{52} e^{k_{2} h} & H_{53} e^{k_{3} h} & H_{54} e^{k_{4} h} & - L_{31} e^{r_{1} h} & - L_{32} e^{r_{2} h} & - L_{33} e^{- r_{1} h} & - L_{34} e^{- r_{2} h} \\ H_{61} e^{k_{1} h} & H_{62} e^{k_{2} h} & H_{63} e^{k_{3} h} & H_{64} e^{k_{4} h} & 0 & 0 & 0 & 0 \end{matrix})}^{- 1} (\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ - P_{1} \\ 0 \end{matrix}) .

5. Numerical results and discussion

The analysis is conducted for aluminum epoxy-like material as [24]: $λ =$ 7.59×10¹⁰ N/m², $μ =$ 1.89××10¹⁰ N/m², $a_{0} =$ 0.61×10^-10 N, $ρ =$ 2.19×10³ kg/m³, $β_{0} = β_{1} =$ 0,05×10⁵ N/(m².k), $c_{e} =$ 966 J/(kg.k), $k =$ 252 J/(m.s.k), $j_{0} =$ 0.196×10^-4 m², $λ_{0} = λ_{1} =$ 0.37×10¹⁰ N/m², $T_{0} =$ 293 k, $τ_{θ} =$ 0.02 s, $τ_{q} =$ 0.5 s, $ω = ω_{0} + i ζ$ , $ω_{0} =$ 3.56, $ζ =$ – 4.81, $b =$ 8, $h =$ 1×10^-6.

The physical constants for elastic medium (granite) as [5]: $λ^{e} =$ 0.884×10¹⁰ N/m², $μ^{e} =$ 1.2667×10¹⁰ N/m², $ρ^{e} =$ 2.6×10³ kg/m³, $c_{e}^{e} =$ 720.7 J/(kg.k), $k^{e} =$ 3.1 J/(m.s.k.)

In light of the results of this paper, the computations are conducted for the value of non-dimensional time $t =$ 0.01, in the range of $0 \leq z \leq 0.4$ on the surface $x =$ 3.01. The numerical strategy stated herein is utilized for the distribution of horizontal displacement $u_{1}$ , the vertical displacement $u_{3}$ , the temperature $T$ , the micro-elongational scalar $φ$ , the stress components $σ_{x x}$ , $σ_{z z}$ and $σ_{x z}$ with distance $z .$ To study the influence of rotation on the solution in the DPL model and the L-S theory and the effect of phase-lag of heat flux and phase-lag of temperature gradient on the solution in the DPL model, this paper introduces the results of the numerical assessment in the form of graphs. The results are shown in Figs. 2-15 for the mechanical force with magnitude $P_{1} = 1$ for the DPL model and the L-S theory.

Fig. 2Distribution of the horizontal displacement u1 with the distance z

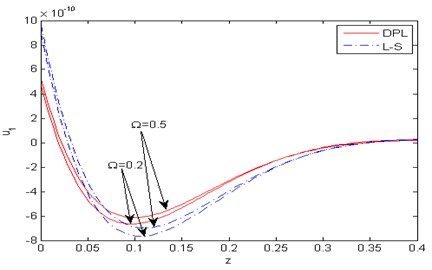
Fig. 3Distribution of the vertical displacement u3 with the distance z

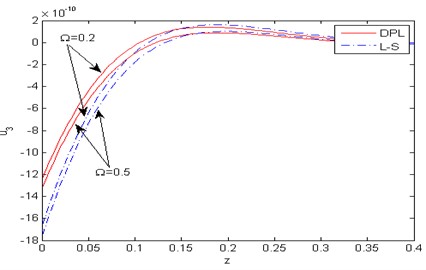
Fig. 4Distribution of the temperature T with distance z

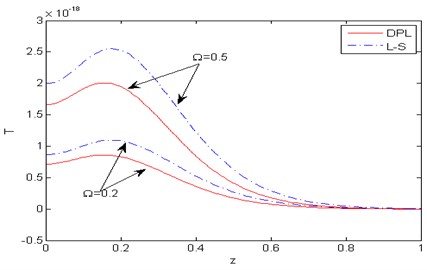
Fig. 5Distribution of the micro-elongational scalar φ with the distance z

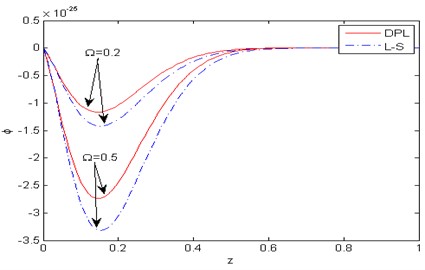
Fig. 6Distribution of the force stress component σxx with the distance z

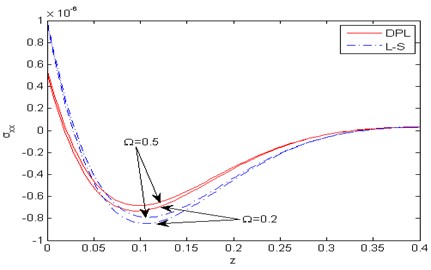
Fig. 7Distribution of the force stress component σzz with the distance z

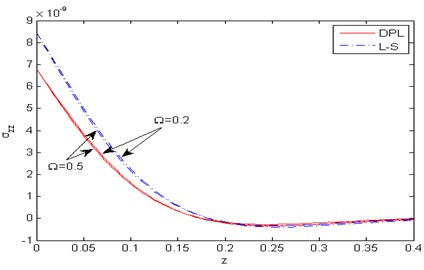
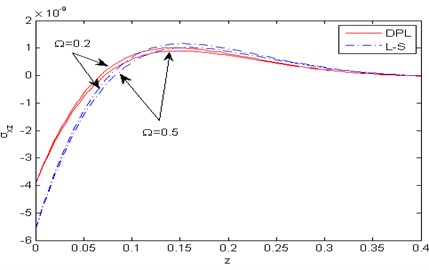
Fig. 8Distribution of the force stress component σxz with horizontal distance z

5.1. Influence of rotation

Figs. 2-8 show comparison between the displacement components $u_{1}$ , $u_{3}$ , the temperature $T$ , the micro-elongational scalar $φ$ and the force stresses components $σ_{x x}$ , $σ_{z z}$ , $σ_{x z}$ for various values of $Ω$ $(Ω =$ 0.2, 0.5) for the DPL model and the L-S theory. Fig. 2 represents the distribution of the horizontal displacement $u_{1}$ with the distance $z$ . It is observed that $u_{1}$ increases with the increase of rotation for the two theories. In the (DPL) model and the L-S theory, the values of the horizontal displacement $u_{1}$ for $Ω =$ 0.2 are small as opposed to those for $Ω =$ 0.5. Fig. 3 illustrates the variation of the vertical displacement $u_{3}$ against the distance $z$ , it is observed that the effect of rotation $Ω$ is inversely proportional to the value of the vertical displacement $u_{3}$ in the DPL model and the L-S theory i.e the rotation $Ω$ has a decreasing effect. Fig. 4 describes the distribution of the temperature $T$ with the distance $z$ . In this figure, all curves start from a positive value and then converge to zero with large values of the distance $z$ and fulfill the boundary condition. It is obvious that the values of the temperature $T$ increases with increase of rotation for the two theories. Fig. 5 shows the variation of the micro-elongational scalar $φ$ against the distance $z$ , it is clear that the values of $φ$ start from zero and decrease to a minimum then increase up to vanish. It is obvious that the values of $φ$ increase with the decrease of rotation for two theories, and satisfies the boundary condition. Fig. 6 is plotted to describe the distribution of the stress components $σ_{x x}$ with the distance $z$ . In this figure, all curves begin from a positive value, then decrease to a minimum and increase up to vanishes at large values of $z$ . The effect of rotation $Ω$ is directly proportional to the value of the stress component $σ_{x x}$ in both the DPL model and the L-S theory. Fig. 7 exhibits the variation of the stress component $σ_{z z}$ against the distance $z$ . In the DPL model, the effect of different values of rotation is hardly visible. It is shown that the influence of rotation is inversely proportional to the value of the stress component $σ_{z z}$ in the L-S theory. Fig. 8 compares among the two different values of rotation for the DPL model and the L-S theory. It is obvious that the value of the stress component $σ_{x z}$ increases as the rotation decreasing.

Fig. 9Distribution of the horizontal displacement u1 with the distance z

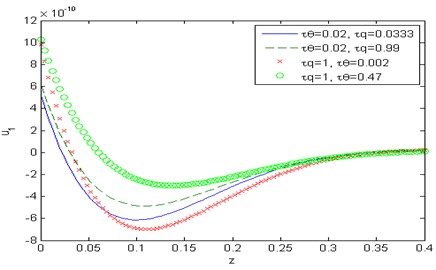
Fig. 10Distribution of the vertical displacement u3 with the distance z

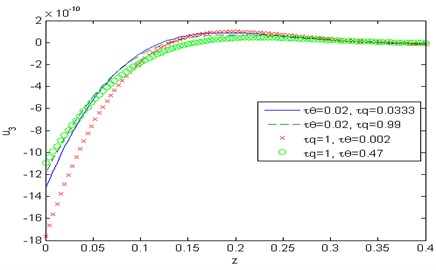
Fig. 11Distribution of the temperature T with distance z

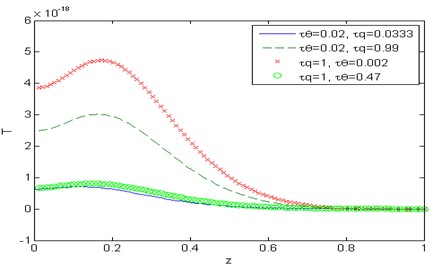
Fig. 12Distribution of the micro-elongational scalar φ with the distance z

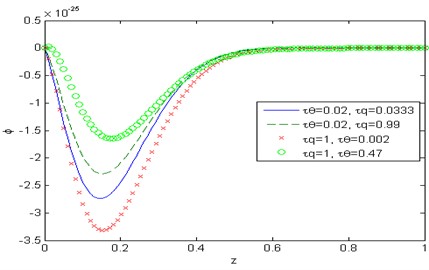
Fig. 13Distribution of the force stress component σxx with the distance z

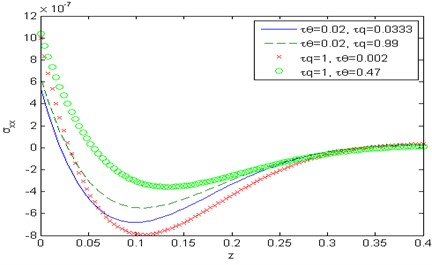
Fig. 14Distribution of the force stress component σzz with the distance z

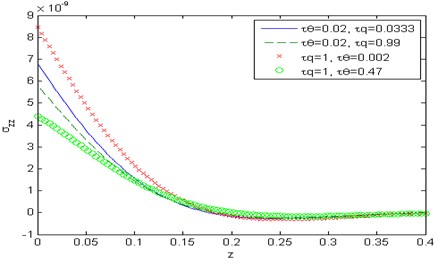
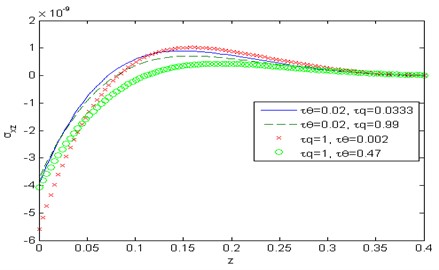
Fig. 15Distribution of the force stress component σxz with the distance z

5.2. Influence of the phase-lag of the heat flux and the phase-lag of temperature gradient

Figs. 9-15 show comparison between the displacement components $u_{1}$ , $u_{3}$ , the temperature $T$ , the micro-elongational scalar $φ$ and the force stress components $σ_{x x}$ , $σ_{z z}$ , $σ_{x z}$ , when it comes to thermoelasticity the DPL model for different values of the temperature gradient phase-lag $τ_{θ}$ , such as $τ_{θ} =$ 0.002, 0.47 at $τ_{q} =$ 1, $Ω =$ 0.5 and for different values of the heat flux phase-lag $τ_{q} =$ 0.0333, 0.99 at $τ_{θ} =$ 0.02, $Ω =$ 0.5. Fig. 9 depicts that the phase-lag of temperature gradient and the heat flux have an increasing effect on the magnitude of the horizontal displacement $u_{1}$ , whereas in fig. 15 they have a decreasing effect on the magnitude of the stress component $σ_{x z}$ in the range 0. $05 \leq z \leq 0.4 .$ Figs. 10 and 13 show that the phase-lag of the heat flux has an increasing effect on the vertical displacement $u_{3}$ over the range $0 \leq z \leq 0.11$ and on the stress component $σ_{x x}$ over the range $0 \leq z \leq 0.4,$ whereas, the phase-lag of the temperature gradient has a decreasing influence on both. Figs. 11 and 14 in that order, exhibit that the temperature $T$ , and the stress component $σ_{z z}$ are inversely proportional to the value of $τ_{q}$ for $z > 0 .$ Fig. 12, explains that the value of micro-elongational scalar $φ$ increases with the increase of $τ_{q}$ and $τ_{θ} .$

5.3. The 3D surface curves

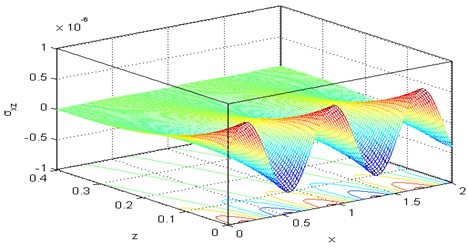
Figs. 16-21 are representing the 3D surface curves for the physical quantities, i.e., the horizontal displacement component $u_{3},$ the micro-elongational scalar $φ$ and the stress components $σ_{x x}$ , $σ_{x z}$ , for the DPL model by keeping in mind the effect of rotation $Ω =$ 0.5. The importance of these figures is that they have been utilized to study the dependence of previous physical quantities on both components of distance.

Fig. 163D curve distribution of the horizontal displacement u1versus distances at Ω=0.5τθ= 0.02, τq= 0.5

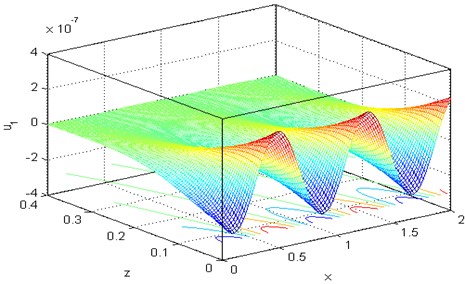
Fig. 173D curve distribution of the vertical displacement u3 versus distances at Ω= 0.5, τθ= 0.02, τq= 0.5

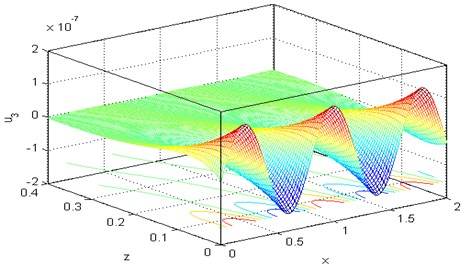
Fig. 183D curve distribution of the micro-elongational scalar φ versus distances at Ω= 0.5, τθ= 0.02, τq = 0.5

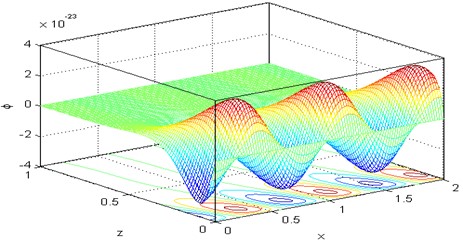
Fig. 193D curve distribution of the force stress component σxx versus distances at Ω= 0.5, τθ= 0.02, τq= 0.5

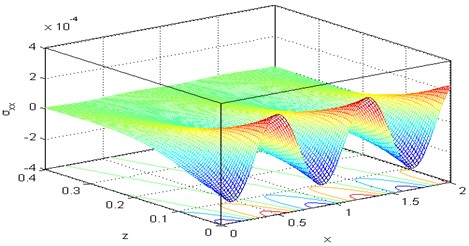
Fig. 203D curve distribution of the force stress component σzz versus distances at Ω= 0.5, τθ= 0.02, τq= 0.5

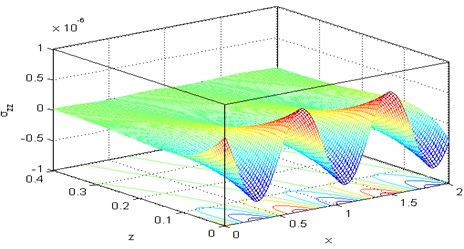
Fig. 213D curve distribution of the force stress component σxz versus distances at Ω= 0.5, τθ= 0.02, τq= 0.5

6. Conclusions

According to the results of this work, one can see that the effect of rotation, the micro-elongational scalar and the applied boundary conditions play a major role in the study of thermoelastic medium deformation. The effect of rotation and the micro-elongational scalar has an obvious influence on all physical quantities. All the physical quantities, converge to zero very steeply with the distance $z$ increases. A comparison between the DPL model and the L-S theory is conducted. An analytical solution depended on normal mode analysis of the problem on thermoelastic micro-elongated layer by encircling finite elastic under influence of the rotation has been developed and used it.

References

S. Shaw and B. Mukhopadhyay, “Periodically varying heat source response in a functionally graded microelongated medium,” Applied Mathematics and Computation, Vol. 218, No. 11, pp. 6304–6313, Feb. 2012, https://doi.org/10.1016/j.amc.2011.11.109

Publisher
S. Shaw and B. Mukhopadhyay, “Moving Heat Source Response in a Thermoelastic Microelongated Solid,” Journal of Engineering Physics and Thermophysics, Vol. 86, No. 3, pp. 716–722, May 2013, https://doi.org/10.1007/s10891-013-0887-y

Publisher
Sunil Kumar Sachdeva and Praveen Ailawalia, “Plane strain deformation in thermoelastic microelongated solid,” Civil and Environmental Research, Vol. 7, No. 2, pp. 92–98, 2015.

Search CrossRef
P. Ailawalia, S. K. Sachdeva, and D. S. Pathania, “Plane strain deformation in a thermoelastic microelongated solid with internal heat source,” International Journal of Applied Mechanics and Engineering, Vol. 20, No. 4, pp. 717–731, Dec. 2015, https://doi.org/10.1515/ijame-2015-0047

Publisher
P. Ailawalia, S. Kumar, and D. S. Pathania, “Internal heat source in thermoelastic microelongated solid under Green Lindsay theory,” Journal of Theoretical and Applied Mechanics, Vol. 46, No. 2, pp. 65–82, Jun. 2016, https://doi.org/10.1515/jtam-2016-0011

Publisher
P. Ailawalia, S. K. Sachdeva, and D. S. Pathania, “A two dimensional problem on laser pulse heating in thermoelastic microelongated solid,” Archives of Thermodynamics, Vol. 40, No. 2, pp. 69–85, 2019, https://doi.org/10.24425/ather.2019.129542

Publisher
P. Ailawalia and A. Singla, “A thermoelastic microelongated layer immersed in an infinite fluid and subjected to laser pulse heating,” Mechanics and Mechanical Engineering, Vol. 23, No. 1, pp. 233–240, Jul. 2019, https://doi.org/10.2478/mme-2019-0031

Publisher
M. I. A. Othman, S. Y. Atwa, E. E. M. Eraki, and M. F. Ismail, “A thermoelastic micro‐elongated layer under the effect of gravity in the context of the dual‐phase lag model,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 101, No. 12, Dec. 2021, https://doi.org/10.1002/zamm.202100109

Publisher
M. I. A. Othman, R. S. Tantawi, and E. E. M. Eraki, “Effect of rotation on a semiconducting medium with two-temperatures under L-S theory,” Archives of Thermodynamics, Vol. 38, No. 2, pp. 101–122, Jun. 2017, https://doi.org/10.1515/aoter-2017-0012

Publisher
H. W. Lord and Y. Shulman, “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, pp. 299–309, Sep. 1967, https://doi.org/10.1016/0022-5096(67)90024-5

Publisher
M. Ezzat, M. Zakaria, O. Shaker, and F. Barakat, “State space formulation to viscoelastic fluid flow of magnetohydrodynamic free convection through a porous medium,” Acta Mechanica, Vol. 119, No. 1-4, pp. 147–164, Mar. 1996, https://doi.org/10.1007/bf01274245

Publisher
M. A. Ezzat and A. A. El-Bary, “Memory-dependent derivatives theory of thermo-viscoelasticity involving two-temperature,” Journal of Mechanical Science and Technology, Vol. 29, No. 10, pp. 4273–4279, Oct. 2015, https://doi.org/10.1007/s12206-015-0924-1

Publisher
M. A. Ezzat, A. S. El-Karamany, and A. A. El-Bary, “Modeling of memory-dependent derivative in generalized thermoelasticity,” The European Physical Journal Plus, Vol. 131, No. 10, pp. 1–12, Oct. 2016, https://doi.org/10.1140/epjp/i2016-16372-3

Publisher
M. A. Ezzat and H. M. Youssef, “Stokes’ first problem for an electro-conducting micropolar fluid with thermoelectric properties,” Canadian Journal of Physics, Vol. 88, No. 1, pp. 35–48, Jan. 2010, https://doi.org/10.1139/p09-100

Publisher
A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, pp. 1–7, Mar. 1972, https://doi.org/10.1007/bf00045689

Publisher
M. N. O. Zis¸Ik and D. Y. Tzou, “On the Wave Theory in Heat Conduction,” Journal of Heat Transfer, Vol. 116, No. 3, pp. 526–535, Aug. 1994, https://doi.org/10.1115/1.2910903

Publisher
D. Y. Tzou, “Experimental support for the lagging behavior in heat propagation,” Journal of Thermophysics and Heat Transfer, Vol. 9, No. 4, pp. 686–693, Oct. 1995, https://doi.org/10.2514/3.725

Publisher
D. Y. Tzou, “A unified field approach for heat conduction from macro – to micro-scales,” Journal of Heat Transfer, Vol. 117, No. 1, pp. 8–16, Feb. 1995, https://doi.org/10.1115/1.2822329

Publisher
A. M. Alharbi, E. M. Abd‐Elaziz, and M. I. A. Othman, “Effect of temperature‐dependent and internal heat source on a micropolar thermoelastic medium with voids under 3PHL model,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 101, No. 6, pp. 1–24, Jun. 2021, https://doi.org/10.1002/zamm.202000185

Publisher
E. M. Abd‐Elaziz and M. I. A. Othman, “Effect of Thomson and thermal loading due to laser pulse in a magneto‐thermo‐elastic porous medium with energy dissipation,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 99, No. 8, Aug. 2019, https://doi.org/10.1002/zamm.201900079

Publisher
M. I. A. Othman and E. M. Abd-Elaziz, “The effect of thermal loading due to laser pulse in generalized thermoelastic medium with voids in dual phase lag model,” Journal of Thermal Stresses, Vol. 38, No. 9, pp. 1068–1082, Sep. 2015, https://doi.org/10.1080/01495739.2015.1073492

Publisher
P. Ailawalia and S. Budhiraja, “Dynamic problem in elastic solid using dual-phase-lag model with internal heat source,” Journal of Mathematical Sciences and Applications, Vol. 2, No. 1, pp. 10–16, 2014, https://doi.org/10.12691/jmsa-2-1-3

Publisher
M. I. A. Othman, W. M. Hasona, and E. M. Abd-Elaziz, “Effect of rotation on micropolar generalized thermoelasticity with two temperatures using a dual-phase lag model,” Canadian Journal of Physics, Vol. 92, No. 2, pp. 149–158, Feb. 2014, https://doi.org/10.1139/cjp-2013-0398

Publisher
M. I. A. Othman and E. M. Abd-Elaziz, “Dual-phase-lag model on micropolar thermoelastic rotating medium under the effect of thermal load due to laser pulse,” Indian Journal of Physics, Vol. 94, No. 7, pp. 999–1008, Jul. 2020, https://doi.org/10.1007/s12648-019-01552-1

Publisher

Cited by

Effect of Inclined Mechanical Load on a Rotating Microelongated Two Temperature Thermoelastic Half Space with Temperature Dependent Properties

Pooja Kadian | Sunil Kumar | Monika Sangwan

(2024)

About this article

Received

17 April 2022

Accepted

12 May 2022

Published

30 June 2022

DOI

https://doi.org/10.21595/jets.2022.22597

Keywords

thermoelasticity

micro-elongation

rotation

normal mode

elastic solid

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 23

Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Baljeet Singh, Himanshu Singla

Research article

2022 11 03

Eigen value approach with memory dependant derivative on homogeneous isotropic infinitely extended rotating plate of a finite thickness in absence of heat source

S. Chakraborty, A. Lahiri, B. Das

Research article

2022 06 30

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Hamdy M. Youssef, Abdullah A. Al Thobaiti

Research article

2021 11 11

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir, Adiya Dar, Mohamed I. A. Othman

M. I. A. Othman, S. Y. Atwa, E. E. M. Eraki, and M. F. Ismail, “Dual-phase-lag model on microelongated thermoelastic rotating medium,” Journal of Engineering and Thermal Sciences, Vol. 2, No. 1, pp. 13–26, Jun. 2022, https://doi.org/10.21595/jets.2022.22597

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2022.22597
UR  - https://doi.org/10.21595/jets.2022.22597
TI  - Dual-phase-lag model on microelongated thermoelastic rotating medium
T2  - Journal of Engineering and Thermal Sciences
AU  - Othman, Mohamed I. A.
AU  - Atwa, Sarhan Y.
AU  - Eraki, E. E. M.
AU  - Ismail, Mohamed F.
PY  - 2022
DA  - 2022/06/30
PB  - JVE International Ltd.
SP  - 13-26
VL  - 2
IS  - 1
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Othman_2022,
	doi = {10.21595/jets.2022.22597},
	url = {https://doi.org/10.21595/jets.2022.22597},
	year = 2022,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {2},
	number = {1},
	pages = {13--26},
	author = {Mohamed I. A. Othman and Sarhan Y. Atwa and E. E. M. Eraki and Mohamed F. Ismail},
	title = {Dual-phase-lag model on microelongated thermoelastic rotating medium},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]M. I. A. Othman, S. Y. Atwa, E. E. M. Eraki, and M. F. Ismail, “Dual-phase-lag model on microelongated thermoelastic rotating medium,” Journal of Engineering and Thermal Sciences, vol. 2, no. 1, pp. 13–26, Jun. 2022, doi: 10.21595/jets.2022.22597.

Copy IEEE

Copied to clipboard!

Othman, Mohamed I. A., Sarhan Y. Atwa, E. E. M. Eraki, and Mohamed F. Ismail. “Dual-Phase-Lag Model on Microelongated Thermoelastic Rotating Medium.” Journal of Engineering and Thermal Sciences 2, no. 1 (June 30, 2022): 13–26. https://doi.org/10.21595/jets.2022.22597.

Copy Chicago

Copied to clipboard!

Dual-phase-lag model on microelongated thermoelastic rotating medium

Abstract

1. Introduction

2. Formulation of the problem

3. Normal mode analysis

4. The boundary conditions

5. Numerical results and discussion

5.1. Influence of rotation

5.2. Influence of the phase-lag of the heat flux and the phase-lag of temperature gradient

5.3. The 3D surface curves

6. Conclusions

References

Cited by

About this article

Related Articles