Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Singh, Baljeet; Singla, Himanshu

doi:10.21595/jets.2023.23268

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 23 December 2023

Check for updates

Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Baljeet Singh¹

Himanshu Singla²

¹Department of Mathematics, Post Graduate Government College, Sector-11, Chandigarh, 160011, India

²Department of Mathematics, Panjab University, Chandigarh, 160014, India

Corresponding Author:

Baljeet Singh

Cite the article Download PDF

Abstract

The governing equations of motion for an isotropic strain-gradient thermoelastic material with diffusion are formulated in context of Lord and Shulman generalization of thermoelasticity and are further specialised for a two dimensional plane. Plane harmonic solution of the governing equations in two-dimension suggests the existence of five plane waves which include four coupled longitudinal waves and a shear vertical wave. A numerical example is considered to illustrate graphically the effect of frequency, measure constant of diffusion, measure constant of thermo-diffusion, thermal relaxation time, diffusive relaxation time and the coefficients of hyperstress tensor on the phase speed and attenuation coefficients of the plane waves.

1. Introduction

Biot [1] gave the theory of coupled thermoelasticty, in which equation of motion and heat conduction equation are coupled. This theory eliminates the first shortcoming of uncoupled theory that elastic changes have no effect on the temperature. To overcome the second shortcoming of uncoupled theory, the non-classical theories of Lord and Shulman [2], Green and Lindsay [3], Green and Naghdi [4] and Tzou [5] came in to existence which are also referred as generalized thermoelastic theories in the literature. Ezzat and his coworkers [6-9] deveoped various new thermoelastic theories by considering various factors including the fractional order, memory-dependent, variable thermal conductivity and phase lag.

A spontaneous movement of particles, from high region concentration to low region concentration is called as diffusion. The coupling of temperature, mass diffusion and strain parameters in an elastic solid is called as thermodiffusion. The diffusion process has many application in fields of oil extractions, integrated circuit fabrication, geophysics and semiconductor industry. The process of thermodiffusion is applied in exploration of the field associated with the advent of semiconductor devices and the advancement of microelectronics. Nowacki [10-12] considered the coupling of elastic, thermal and diffusion parameters and developed a coupled theory of thermodiffusion. Further, Sherief et al. [13] derived the governing equations for a theory of generalized thermodiffusion in elastic solids. Aoudai [14] considered the uniqueness and reciprocity theorem in elastic media with generalized thermoelastic diffusion. Ezzat and Fayik [15] applied fractional calculus to derive an another theory of thermodiffusion in elastic solids. Karamany and Ezzat [16] introduced a theory of generalized thermodiffusion which was based on the memory-dependent derivatives. Recently, Li et al. [17] and Abouelregal [18] studied the effects of thermodiffusion in various anisotropic devices.

The gradient theory of elasticity is considered to be adequate for investigating important problems related to size effects, chiral materials and nanotechnology. The origin of the strain gradient theories of nonsimple elastic solids goes back to works of Toupin [19] and Mindlin and Eshel [20]. Aifantis [21] formulated gradient elasticity theories for infinitesimal deformations. Recently, Iesan and Quintanilla [22] developed the strain gradient theory of thermoviscoelasticity. There are various applications of strain gradient theories in literature including Ahmadi and Firoozbakhsh [23], Aifantis ([24], [25]), Forest et al. [26], Forest and Aifantis [27], Iesan and Quintanilla ([28] and [29]). Aouadi et al. [30] developed a consistent nonlinear theory of strain gradient theory for thermoelastic diffusion materials and derived the basic equation of nonlinear strain gradient theory of thermoelasticity with mass diffusion effect.

Wave propagation in thermoelastic materials is a topic of interest for many researchers since last many decades. Chadwick and Sneddon [31] studied the plane wave in a thermoelastic solid. Puri [32] studied the plane waves in generalized thermoelastic solid in context of Lord Shulman theory. Agarwal [33] studied the plane waves in generalized thermoelastic solid in context of both Green Lindsay and Lord-Shulman theories. Sharma et al. [34] studied the plane harmonic waves in orthorhombic heat conducting materials. Verma and Hasebe [35] studied the wave propagation in plates of general anisotropic media. Singh ([36], [37]) explored the plane wave characteristics in a generalized thermoelastic medium with diffusion in context of Lord-Shulman, Green-Lindsay and Green-Nagdhi theories. Various other research works on wave propagation in thermoelastic diffusive materials are also available in literature, which include Othman et al. [38], Kumar and Gupta [39], Deswal et al. [40].

No theoretical/numerical study is traced in literature yet which investigated the characteristics of plane waves in a strain-gradient generalized thermoelastic medium with the effects of diffusion/mass transfer. Motivated by the strain gradient theory of thermoelastic diffusive material given by Aouadi et al. [30], the plane wave characteristics are investigated in an isotropic strain-gradient thermoelastic diffusive material. In Section 2, the governing equations of an isotropic model are derived with the help of Lord and Shulman [2] and Aouadi et al. [30]. In Section 3, the governing equations are specialized for a plane. These specialized equations are solved in Section 4 to explore the possibility of plane waves in the model. Two velocity equations for plane waves are derived which suggest the propagation of four coupled longitudinal waves and a shear vertical wave. Some special cases of these velocity equations are also derived in absence of diffusion parameters or hyperstress coefficients or both parameters. A numerical example of Magnesium is considered in Section 5 to illustrate graphically the phase speeds and attenuation coefficients of plane waves. The theoretical and numerical findings of the present work are presented in the last section.

2. Governing equations of an isotropic model

In absence of body forces and external heat sources, the governing equations of an isotropic strain-gradient thermoelastic diffusive material are formulated in context of Aouadi et al. [30] and Lord and Shulman [2] theories as.

(a) Equations of motion:

1

ρ \frac{\partial^{2} u_{i}}{\partial t^{2}} = μ \nabla^{2} u_{i} - ν_{1} \nabla^{4} u_{i} + (μ + λ_{0}) \frac{\partial u_{j}}{\partial x_{j} \partial x_{i}} - ν_{2} \nabla^{2} \frac{\partial u_{j}}{\partial x_{j} \partial x_{i}} - γ_{1} \frac{\partial Θ}{\partial x_{i}} - γ_{2} \frac{\partial P}{\partial x_{i}} .

(b) Heat conduction equation:

2

(1 + τ_{0} \frac{\partial}{\partial t}) (γ_{1} \frac{\partial e_{k k}}{\partial t} + C_{e} \frac{\partial Θ}{\partial t} + d \frac{\partial P}{\partial t}) = κ \nabla^{2} θ .

(c) Mass diffusion equation:

3

(1 + τ_{1} \frac{\partial}{\partial t}) (γ_{2} \frac{\partial e_{k k}}{\partial t} + d \frac{\partial Θ}{\partial t} + r \frac{\partial P}{\partial t}) = h \nabla^{2} P,

where:

γ_{1} = β_{1} + \frac{a β_{2}}{b}, γ_{2} = \frac{β_{2}}{b}, λ_{0} = λ - \frac{β_{2}^{2}}{b}, C_{e} = \frac{ρ c_{E}}{T_{0}} + \frac{a^{2}}{b}, d = \frac{a}{b}, r = \frac{1}{b},

β_{1} = (3 λ + 2 μ) α_{t}, β_{2} = (3 λ + 2 μ) α_{c}, \nabla^{2} = \frac{\partial^{2}}{\partial x_{1}^{2}} + \frac{\partial^{2}}{\partial x_{2}^{2}} + \frac{\partial^{2}}{\partial x_{3}^{2}},

in which $ρ$ is the density of material, $λ$ , $μ$ are the Lame’s constants, $κ$ is coefficient of thermal conductivity, $h$ is the coefficient of mass diffusion conductivity, $ν_{1}$ , $ν_{2}$ are constitutive coefficients of hyperstress tensor, $a$ is the measure constant of thermo-diffusive effect, $b$ is the measure constant of diffusive effect, $τ_{0}$ is the thermal relaxation time, $τ_{1}$ is the diffusion relaxation time, $c_{E}$ is the specific heat at constant strain, $α_{t}$ is coefficient of linear thermal expansion, $α_{c}$ is the coefficient of linear diffusion expansion, $P$ is the chemical potential per unit mass of diffusive material, $Θ$ is increment in temperature, $T_{0}$ is the temperature of the body in natural state, $u_{i}$ is the displacement vector, $e_{i j}$ are the components of strain tensor, $e_{k k} = u_{k, k}$ , $x_{i}$ and $x_{j}$ are dependent variables and $\nabla^{2}$ is the Laplace operator.

3. Specialization in two-dimension

A half-space of an isotropic thermoelastic material with diffusion in strain gradient theory is considered in rectangular Cartesian coordinate system ( $x_{1}, x_{2}, x_{3}$ ) having the surface of the half-space as the plane $x_{3} = 0 .$ Therefore, the present analysis is restricted to $x_{1} - x_{3}$ plane. The following components of displacement vector are taken as Eq. (4):

4

u_{1} = u_{1} (x_{1}, x_{3}, t), u_{3} = u_{3} (x_{1}, x_{3}, t), u_{2} = 0 .

Using the Helmholtz decomposition theorem on vectors, the components of displacement vectors are written in terms of scalar potentials functions $ϕ_{1}$ , $ϕ_{3}$ as Eq. (5):

5

u_{1} = \frac{\partial ϕ_{1}}{\partial x_{1}} - \frac{\partial ϕ_{3}}{\partial x_{3}}, u_{3} = \frac{\partial ϕ_{1}}{\partial x_{3}} + \frac{\partial ϕ_{3}}{\partial x_{1}} .

Using Eqs. (4) and (5), the Eqs. (1) to (3) are specialized in $x_{1} - x_{3}$ plane as Eqs. (6-9):

6

((λ_{0} + 2 μ) \nabla^{2} - ρ \frac{\partial^{2}}{\partial t^{2}}) ϕ_{1} - ν_{1} \nabla^{4} ϕ_{1} - ν_{2} \nabla^{4} ϕ_{1} - γ_{1} Θ - γ_{2} P = 0,

7

μ \nabla^{2} ϕ_{3} - ν_{1} \nabla^{4} ϕ_{3} = ρ \frac{\partial^{2} ϕ_{3}}{\partial t^{2}},

8

(1 + τ_{0} \frac{\partial}{\partial t}) (γ_{1} T_{0} \nabla^{2} \frac{\partial ϕ_{1}}{\partial t} + C_{e} T_{0} \frac{\partial Θ}{\partial t} + d T_{0} \frac{\partial P}{\partial t}) = κ \nabla^{2} θ,

9

(1 + τ_{1} \frac{\partial}{\partial t}) (γ_{2} \nabla^{2} \frac{\partial ϕ_{1}}{\partial t} + d \frac{\partial Θ}{\partial t} + r \frac{\partial P}{\partial t}) = h \nabla^{2} P .

Here, the Eqs. (6), (8) and (9) are coupled in $ϕ_{1}$ , $Θ$ and $P$ and Eq. (7) is uncoupled in $ϕ_{3}$ .

4. Plane wave solution

To solve the Eqs. (6) to (9), the plane harmonic waves propagating with wave normal lying in the $x_{1} - x_{3}$ plane and making an angle $θ$ with the $x_{3}$ -axis is considered. Then, the following form of plane harmonic solutions are considered as Eq. (10):

10

{ϕ_{1}, ϕ_{3}, Θ, P} = \{{\bar{ϕ}}_{1}, {\bar{ϕ}}_{3}, \bar{Θ}, \bar{P},\} \exp (i k (x_{1} s i n θ + x_{3} c o s θ) - i ω t),

where, $i = \sqrt{- 1}$ , $k$ is wave number, $ω$ is angular frequency, ${\bar{ϕ}}_{1}$ , $\bar{Θ}$ , $\bar{P}$ and ${\bar{ϕ}}_{3}$ are arbitrary constants and the pair ( $s i n θ$ , $c o s θ$ ) denote the projection of the wave normal on to $x_{1} - x_{3}$ plane. The homogeneous system of Eqs. (11-14) is obtained by inserting Eq. (10) into Eqs. (6) to (9):

11

[k^{4} ν + (k^{2} c_{1}^{2} - ω^{2})] {\bar{ϕ}}_{1} + {\bar{γ}}_{1} {\bar{θ}}_{1} + {\bar{γ}}_{2} \bar{P} = 0,

12

K_{1} k^{2} ω^{2} {\bar{ϕ}}_{1} + (K_{2} k^{2} - ω^{2}) \bar{θ} - K_{3} ω^{2} \bar{P} = 0,

13

d_{1} k^{2} ω^{2} {\bar{ϕ}}_{1} - d_{2} ω^{2} \bar{θ} + (d_{3} k^{2} - ω^{2}) \bar{P} = 0,

14

(b_{1} k^{4} + c_{2}^{2} k^{2} - ω^{2}) {\bar{ϕ}}_{3} = 0,

where:

c_{1}^{2} = \frac{λ + 2 μ}{ρ}, c_{2}^{2} = \frac{μ}{ρ}, {\bar{γ}}_{1} = \frac{γ}{ρ}, {\bar{γ}}_{2} = \frac{γ_{2}}{ρ}, K_{1} = \frac{γ_{1}}{C_{e}}, K_{2} = \frac{κ}{C_{e} T_{0} τ_{0}^{*}},

ν = ν_{1} + ν_{2}, K_{3} = \frac{d}{C_{e}}, d_{1} = \frac{γ_{2}}{r}, d_{2} = \frac{d}{r}, d_{3} = \frac{h}{r τ_{1}^{*}}, τ_{0}^{*} = τ_{0} + \frac{ι}{ω},

τ_{1}^{*} = τ_{1} + \frac{ι}{ω}, b_{1} = \frac{ν_{1}}{ρ} .

The system of Eqs. (11) to (13) admits non-trivial solution if and only if determinant of coefficient matrix vanishes, i.e.:

15

|\begin{matrix} k^{4} ν + (k^{2} c_{1}^{2} - ω^{2}) & {\bar{γ}}_{1} & {\bar{γ}}_{2} \\ K_{1} k^{2} ω^{2} & (K_{2} k^{2} - ω^{2}) & - K_{3} ω^{2} \\ d_{1} k^{2} ω^{2} & - d_{2} ω^{2} & (d_{3} k^{2} - ω^{2}) \end{matrix}| = 0,

which is expanded as following bi-quadratic equation in $k^{2}$ :

16

S_{0} (k^{2})^{4} + S_{1} (k^{2})^{3} + S_{2} (k^{2})^{2} + S_{3} (k^{2}) + S_{4} = 0,

where:

S_{0} = d_{3} K_{2} ν, S_{1} = c_{1}^{2} d_{3} K_{2} - (d_{3} + K_{2}) ω^{2} ν - K_{2} ω^{2} ν,

S_{2} = (ω^{2})^{2} ν - c_{1}^{2} d_{3} ω^{2} - c_{1}^{2} K_{2} ω^{2} - d_{3} K_{2} ω^{2} - d_{1} {\bar{γ}}_{2} K_{2} ω^{2} - d_{3} {\bar{γ}}_{1} K_{1} ω^{2} - d_{2} K_{3} (ω^{2})^{2} ν,

S_{3} = c_{1}^{2} (ω^{2})^{2} + d_{3} (ω^{2})^{2} + K_{2} (ω^{2})^{2} + d_{1} {\bar{γ}}_{2} (ω^{2})^{2} + {\bar{γ}}_{1} K_{1} (ω^{2})^{2} - c_{1}^{2} d_{2} K_{3} (ω^{2})^{2} - d_{1} {\bar{γ}}_{1} K_{3} (ω^{2})^{2} - d_{2} {\bar{γ}}_{2} K_{1} (ω^{2})^{2},

S_{4} = ω^{6} (d_{2} K_{3} - 1) .

The four roots of velocity Eq. (16) correspond to four coupled longitudinal plane waves. The phase speed $V_{i}$ ( $i =$ 1, 2,..., 4) and the attenuation coefficients $Q_{i}$ ( $i =$ 1, 2,..., 4) of the plane waves $P_{i}$ ( $i =$ 1, 2,…, 4) may be obtained by using following formulae:

17

V_{i} = \frac{ω}{R e (k_{i})}, Q_{i} = | I m a g (k_{i}) |,

where $R e (k_{i})$ and $I m a g (k_{i})$ are the real and imaginary part of $k_{i} .$ The solution of Eq. (14) correspond to the SV wave with speed:

18

V_{5} = \sqrt{c_{2}^{2} + b_{1} k^{2}} .

4.1. In absence of hyperstress coefficients

In absence of hyperstress coefficients, the velocity Eq. (15) reduces to the Eq. (19):

19

|\begin{matrix} (k^{2} c_{1}^{2} - ω^{2}) & {\bar{γ}}_{1} & {\bar{γ}}_{2} \\ K_{1} k^{2} ω^{2} & (K_{2} k^{2} - ω^{2}) & - K_{3} ω^{2} \\ d_{1} k^{2} ω^{2} & - d_{2} ω^{2} & (d_{3} k^{2} - ω^{2}) \end{matrix}| = 0 .

The cubic Eq. (19) indicates the propagation of three coupled longitudinal waves. In absence of hyperstress coefficients, the speed of SV wave given in Eq. (18) will reduce to the speed of classical SV wave as given by Eq. (20):

20

V_{5} = \sqrt{\frac{μ}{ρ}} .

The reduced velocity Eqs. (19) and (20) are in agreement with Singh [36].

4.2. In absence of diffusion parameters

In absence of diffusion parameters, the velocity Eq. (15) reduces to Eq. (21):

21

|\begin{matrix} k^{4} ν + (k^{2} c_{1}^{2} - ω^{2}) & {\bar{γ}}_{1} \\ K_{1} k^{2} ω^{2} & (K_{2} k^{2} - ω^{2}) = 0 \end{matrix}| = 0 .

The cubic Eq. (21) indicates the propagation of three coupled longitudinal waves. The speed of SV wave given by equation (18) is independent of diffusion parameters.

4.3. In absence of both diffusion and hyperstress coefficients

In absence of diffusion and hyperstress coefficients, the Eq. (15) reduces to Eq. (22):

22

|\begin{matrix} (k^{2} c_{1}^{2} - ω^{2}) & {\bar{γ}}_{1} \\ K_{1} k^{2} ω^{2} & (K_{2} k^{2} - ω^{2}) \end{matrix}| = 0 .

The quadratic Eq. (22) suggests the propagation of two coupled plane waves. In absence of diffusion and hyperstress coefficients, the speed of SV wave given in Eq. (18) will reduce to the speed of classical SV wave as given by Eq. (20).

5. Numerical results and discussion

The objective of present numerical simulations is to check the variations of phase speeds and attenuation coefficients for a specific material. The following material constants of Magnesium at $T_{0} =$ 300 K from Singh [41] are considered to compute the phase speeds and attenuation coefficients as in Table 1.

Using above above physical constants and using Eq. (17), the velocity Eq. (16) is solved to obtain the speeds and attenuations coefficients of four coupled longitudinal waves. The velocity Eq. (18) is also solved to obtain the speed of the $S V$ wave. The wave speeds and attenuation coefficients of four coupled longitudinal waves ( $P_{1}$ , $P_{2}$ , $P_{3}$ and $P_{4}$ ) are plotted in Fig. 1 against the circular frequency $ω$ for three different values of measure constant of thermo-diffusive effect $a$ For all values of $a$ , the illustrations in figure 1 shows that the speeds and attenuation coefficients of all coupled longitudinal increase nonlinearly as the circular frequency $ω$ increases. For increasing value of frequency, the rate of increase in speeds of $P_{1}$ and $P_{2}$ waves become fast and the rate of increase in speeds of $P_{3}$ and $P_{4}$ waves becomes slow. The effect of measure constant of thermodiffusion $a$ is observed on $P_{1}$ and $P_{3}$ waves as these waves become faster as value of $a$ is increased at a given frequency $ω$ . This effect of thermodiffusion on $P_{1}$ and $P_{3}$ waves becomes more considerable as the frequency $ω$ increases. For the selected range of frequency, the speeds of $P_{2}$ and $P_{4}$ waves are not influenced considerably by changing the values of constant $a$ . The variations of the attenuation coefficients of the coupled longitudinal waves except $P_{1}$ wave are also affected due to change in values of constant $a$ at a given frequency.

Fig. 1The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when measure constant of thermo-diffusive effect a = 0.005 (solid line), a = 0.05 (dotted line) and a = 0.5 (dashed line)

The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when measure constant of thermo-diffusive effect a = 0.005 (solid line), a = 0.05 (dotted line) and a = 0.5 (dashed line)

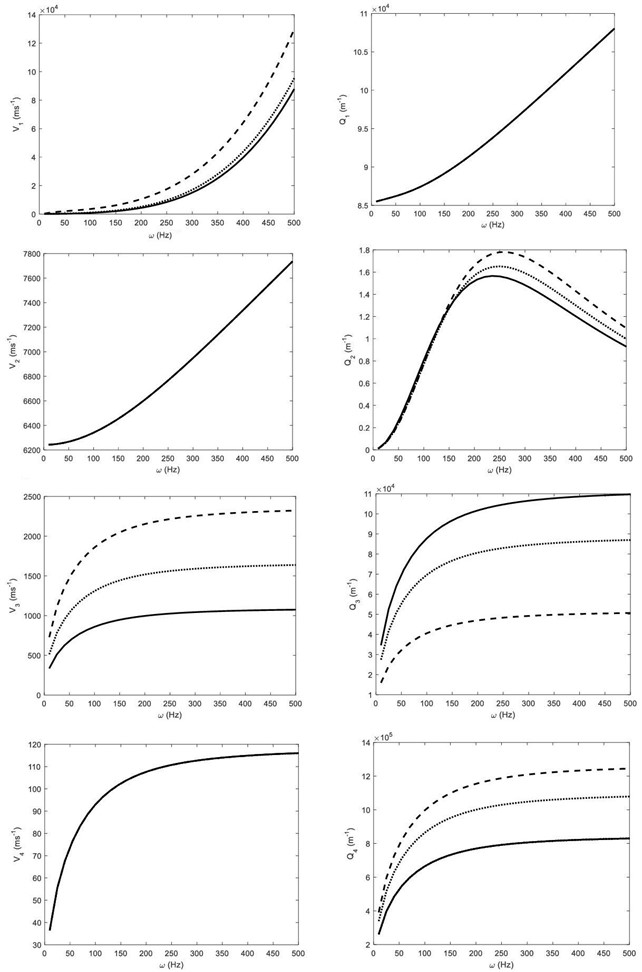
Table 1Material constants of magnesium

Symbol	Value	Unit	Symbol	Value	unit
$λ$	3.17 $\times 1 0^{10}$	Nm^–2	$μ$	1.639×10¹⁰	Nm^–2
$ρ$	1740	Kgm^–3	$C_{E}$	2361	JKg^–1deg^–1
$κ$	49.2	Wm^–1deg^–1	$h$	0.85	Kgsm^–3
$α_{t}$	0.005	deg^–1	$α_{c}$	0.005	m³Kg^–1
$a$	0.005	m^–2s^–2deg^–1	$B$	0.005	m⁵kg^–1s^–2
$τ_{0}$	0.005	s	$τ_{1}$	0.005	s
$ν_{1}$	0.002	Kgm^–1s^–2	$ν_{2}$	0.002	Kgm^–1s^–2

Fig. 2The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when measure constant of diffusive effect b = 0.005 (solid line), b = 0.05 (dotted line) and b = 0.5 (dashed line)

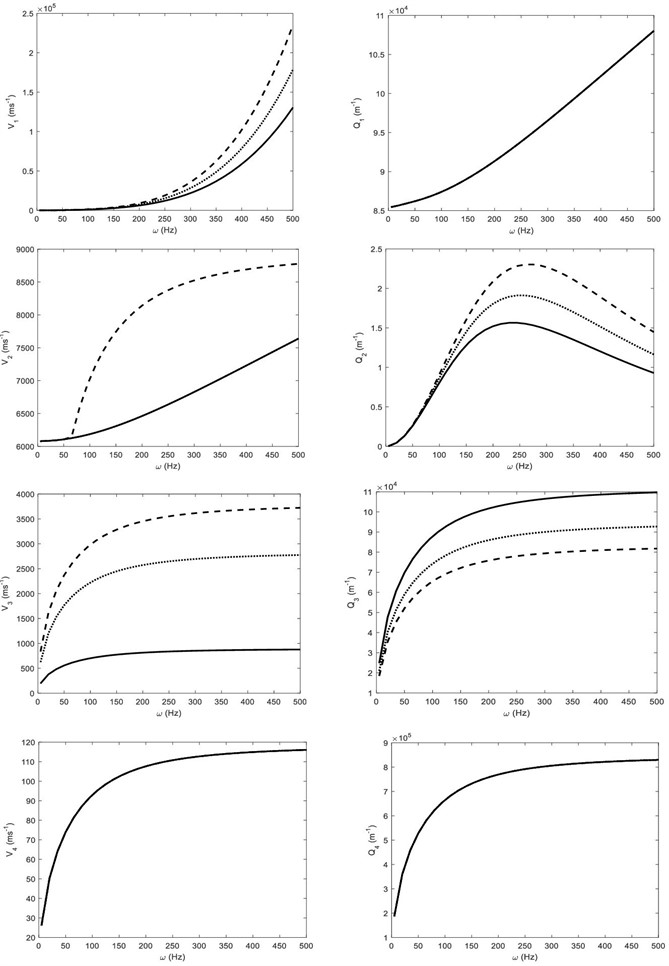
The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when measure constant of diffusive effect b = 0.005 (solid line), b = 0.05 (dotted line) and b = 0.5 (dashed line)

The wave speeds and attenuation coefficients of four coupled longitudinal waves ( $P_{1}$ , $P_{2}$ , $P_{3}$ and $P_{4}$ ) are plotted in Fig. 2 against the circular frequency $ω$ for three different values of measure constant of diffusive effect $b$ . The effect of measure constant of diffusion $b$ is observed on $P_{1}, P_{2}$ and $P_{3}$ waves as these waves become faster as value of $b$ is increased at a given frequency $ω$ . The diffusion effect on $P_{1}$ , $P_{2}$ and $P_{3}$ waves becomes more considerable as the frequency $ω$ increases. For the selected range of frequency, the speed $P_{4}$ wave is not influenced considerably by changing the values of constant $b$ . The attenuation coefficients of the coupled longitudinal waves except $P_{1}$ and $P_{4}$ waves are also affected due to change in diffusion constant $a$ at a given frequency.

Fig. 3The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when thermal relaxation time τ0 = 0.005 (solid line), τ0 = 0.05 (dotted line) and τ0 = 0.5 (dashed line)

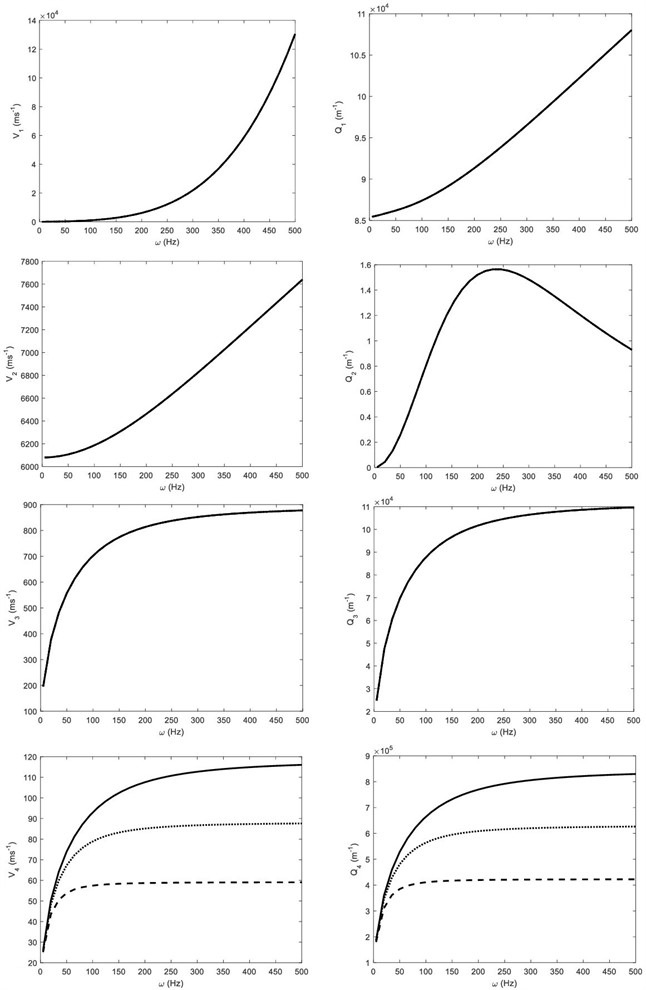
The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when thermal relaxation time τ0 = 0.005 (solid line), τ0 = 0.05 (dotted line) and τ0 = 0.5 (dashed line)

The wave speeds and attenuation coefficients of four coupled longitudinal waves ( $P_{1}$ , $P_{2}$ , $P_{3}$ and $P_{4}$ ) are plotted in Fig. 3 against the circular frequency $ω$ for three different values of thermal relaxation time $τ_{0}$ . The effect of thermal relaxation is observed on the speed and attenuation coefficient of $P_{4}$ wave only. The speed of $P_{4}$ wave becomes slow as the value of $τ_{0}$ increases at a given frequency. The effect of thermal relaxation time on speed and attenuation of $P_{4}$ wave becomes more considerable as the frequency increases.

Fig. 4The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when diffusion relaxation time τ1 = 0.005 (solid line), τ1 = 0.05 (dotted line) and τ1 = 0.5 (dashed line)

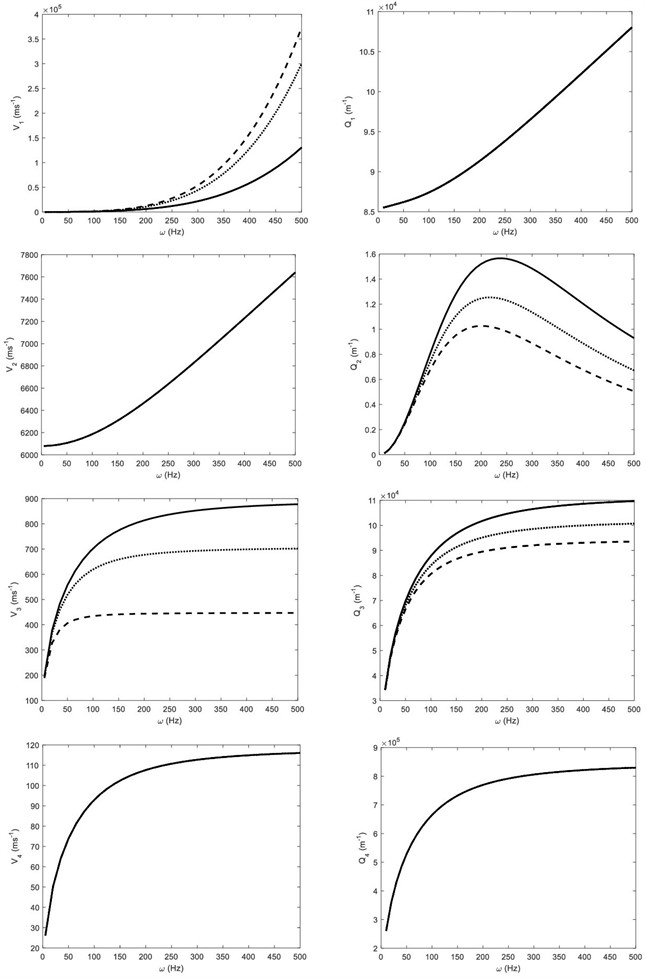
The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when diffusion relaxation time τ1 = 0.005 (solid line), τ1 = 0.05 (dotted line) and τ1 = 0.5 (dashed line)

The wave speeds and attenuation coefficients of four coupled longitudinal waves ( $P_{1}$ , $P_{2}$ , $P_{3}$ and $P_{4}$ ) are plotted in Fig. 4 against the circular frequency $ω$ for three different values of diffusion relaxation time $τ_{1}$ . The effect of diffusion relaxation time is observed on the speeds of $P_{1}$ and $P_{3}$ waves and on attenuation coefficient of $P_{2}$ and $P_{3}$ waves. For a given frequency, the speed of $P_{1}$ becomes faster as the value of $τ_{1}$ increases, whereas the speed of $P_{3}$ waves becomes slower. This effect of diffusion relaxation time on these coupled waves becomes more considerable as the value of circular frequency increases.

Fig. 5The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when the coefficient of hyperstress tensor ν = 0.005 (solid line), ν = 0.05 (dotted line) and ν = 0.5 (dashed line)

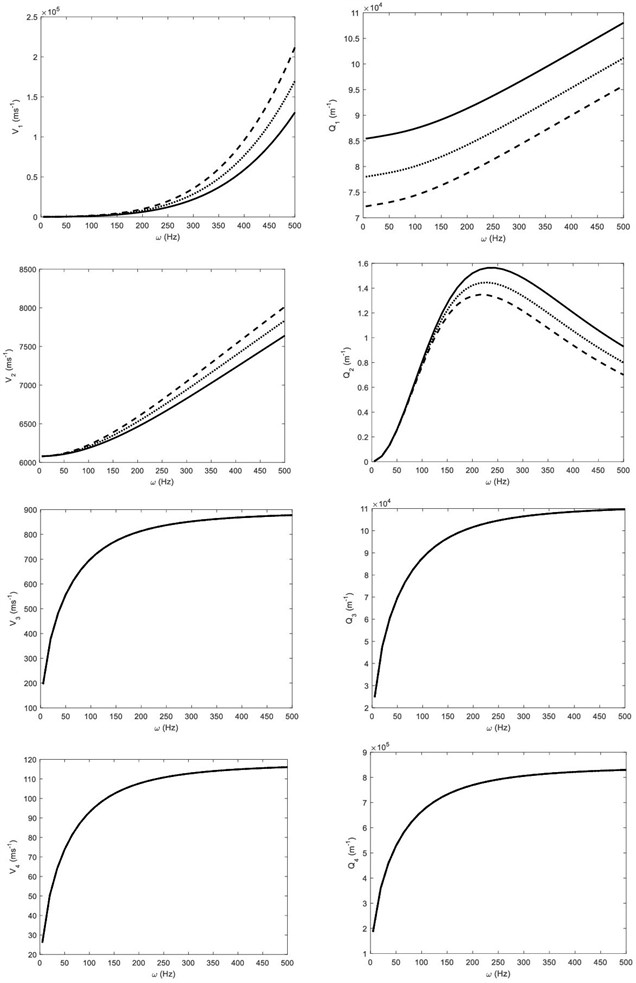
The wave speeds and attenuation coefficients of the P1, P2, P3 and P4 waves against frequency ω, when the coefficient of hyperstress tensor ν = 0.005 (solid line), ν = 0.05 (dotted line) and ν = 0.5 (dashed line)

The wave speeds and attenuation coefficients of four coupled longitudinal waves ( $P_{1}$ , $P_{2}$ , $P_{3}$ and $P_{4}$ ) are plotted in Fig. 5 against the circular frequency $ω$ for three different values of hyperstress coefficient $ν$ . The effect of hyperstress is observed on the speeds and attenuations of $P_{1}$ and $P_{2}$ waves. For a given frequency, the speeds of $P_{1}$ and $P_{2}$ becomes faster as the value of $ν$ increases. This effect of hyperstress on these coupled waves becomes more considerable as the value of circular frequency increases.

The wave speeds and attenuation coefficients of coupled longitudinal waves are also plotted in Fig. 6 (in absence of hyperstress) where $P_{2}$ wave will not propagate in absence of hyperstress. The wave speeds and attenuation coefficients of coupled longitudinal waves are plotted in Fig. 7 (in absence of diffusion) where $P_{3}$ wave will not propagate in absence of diffusion. In Fig. 8, the wave speeds and attenuation coefficients of coupled longitudinal waves are shown graphically in absence of both diffusion and hyperstress, where the $P_{1}$ and $P_{4}$ waves will propagate.

Fig. 6The wave speeds and attenuation coefficients of the P1, P3 and P4 waves against frequency ω (in absence of hyperstress)

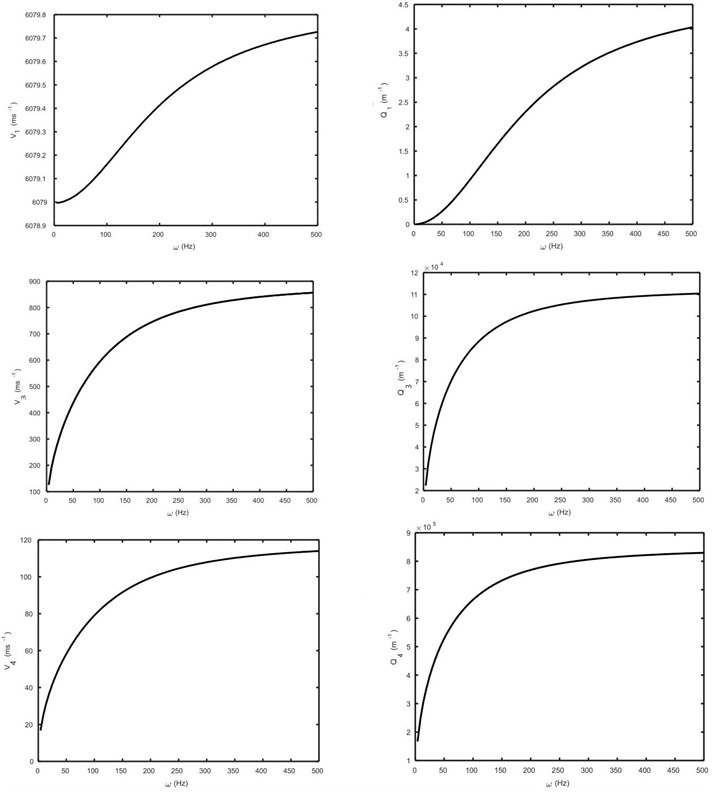
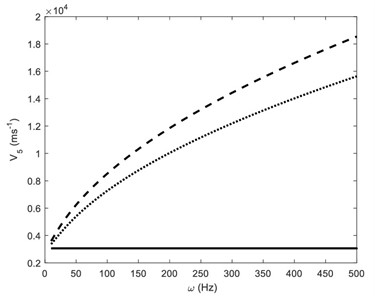
The wave speed of $S V$ wave is plotted in Fig. 9 against the circular frequency $ω$ for three different values of hyperstress coefficient $ν$ . In presence of hyperstress, the speed of $S V$ wave increases nonlinearly as the frequency increases. For a given frequency, the speed of $S V$ becomes faster as the value of $ν$ increases. This effect of hyperstress on the $S V$ wave is observed more considerable as the value of circular frequency increases.

Fig. 7The wave speeds and attenuation coefficients of the P1, P2 and P4 waves against frequency ω (in absence of diffusion)

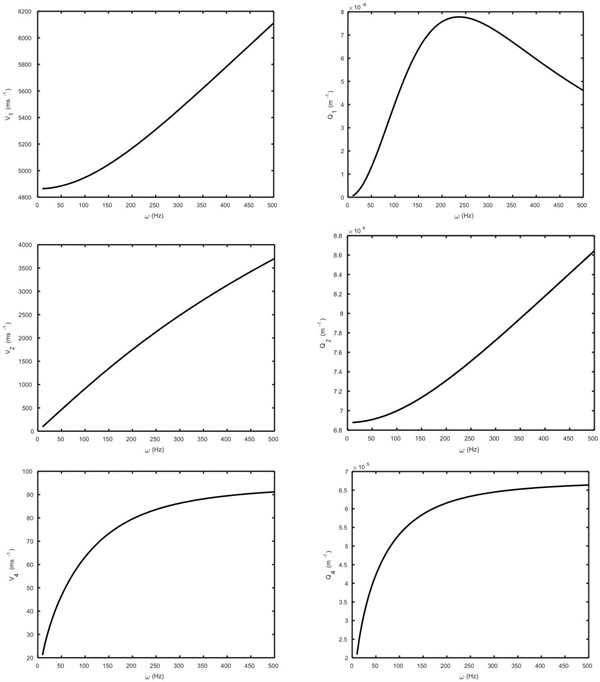
Fig. 8The wave speeds and attenuation coefficients of the P1 and P4 waves against frequency ω (in absence of hyperstress and diffusion)

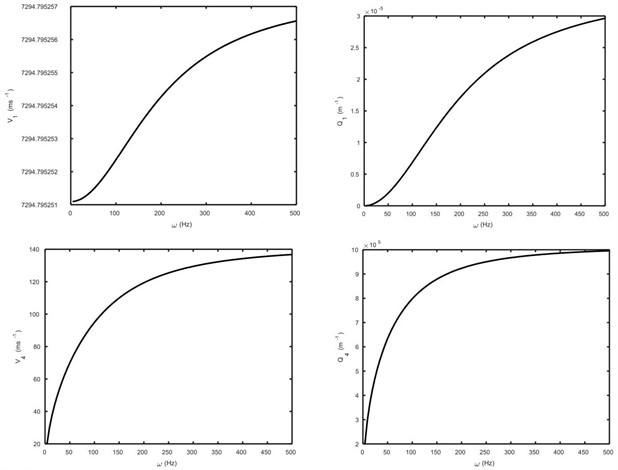
Fig. 9The wave speed of the SV wave against frequency ω, when coefficient of hyperstress tensor ν1 = 0(solid line), ν = 0.005 (dotted line) and ν = 0.05 (dashed line)

The wave speed of the SV wave against frequency ω, when coefficient of hyperstress tensor ν1 = 0(solid line), ν = 0.005 (dotted line) and ν = 0.05 (dashed line)

6. Conclusions

A problem on propagation of plane waves is considered in an isotropic, linear and homogeneous strain-gradient thermoelastic diffusive medium. The governing equations are formulated in context of Aoudai et al. [30] and Lord and Shulman [2] theories and are specialized in two-dimension. Two velocity equations for plane waves are derived, which suggest the propagation of four coupled longitudinal waves and a shear vertical wave. The numerical computations in MATLAB for a specific material (Magnesium) ensure the existence of these waves. The graphical illustrations show that the wave speeds and attenuation coefficients of these waves are affected by the circular frequency, measure constants of diffusion and thermo-diffusion, thermal and diffusion relaxation times and the coefficient of hyperstress tensor. Following some important observations are made from the present numerical results:

1) The speeds and attenuation coefficients of coupled longitudinal waves increase nonlinearly as the frequency increases.

2) For a given value of frequency, the $P_{1}$ and $P_{3}$ waves travel faster as the measure constant $a$ increases and the $P_{1}$ , $P_{2}$ and $P_{3}$ waves travel faster as the measure constant $b$ increases.

3) The effect of thermal relaxation is observed on the speed and attenuation coefficient of $P_{4}$ wave only. The speed of $P_{4}$ wave becomes slow as the value of $τ_{0}$ increases at a given frequency. The effect of diffusion relaxation time is observed on the speeds of $P_{1}$ and $P_{3}$ waves and on attenuation coefficient of $P_{2}$ and $P_{3}$ waves. For a given frequency, the speed of $P_{1}$ becomes faster as the value of $τ_{1}$ increases, whereas the speed of $P_{3}$ waves becomes slower.

4) The effect of hyperstress is observed on the speeds and attenuations of $P_{1}$ and $P_{2}$ waves. For a given frequency, the speeds of $P_{1}$ and $P_{2}$ becomes faster as the value of $ν$ increases.

5) The effects of measure constants of diffusion and thermo-diffusion, thermal and diffusion relaxation times and the coefficients of hyperstress tensor becomes more considerable as the frequency increases.

6) In absence of hyperstress or diffusion parameters, the number of coupled longitudinal waves will reduce to three. In absence of hyperstress coefficients, the $P_{2}$ wave will not propagate and the $P_{3}$ wave will not propagate in the absence of diffusion.

7) In presence of hyperstress, the speed of $S V$ wave increases nonlinearly against the frequency. For a given frequency, the the $S V$ wave travels faster as the value of $ν$ increases. This effect of hyperstress on the $S V$ wave is observed more considerable as the frequency increases.

References

M. A. Biot, “Thermoelasticity and irreversible thermodynamics,” Journal of Applied Physics, Vol. 27, No. 3, pp. 240–253, Mar. 1956, https://doi.org/10.1063/1.1722351

Publisher
H. W. Lord and Y. Shulman, “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, pp. 299–309, Sep. 1967, https://doi.org/10.1016/0022-5096(67)90024-5

Publisher
A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, pp. 1–7, Mar. 1972, https://doi.org/10.1007/bf00045689

Publisher
A. E. Green and P. M. Naghdi, “Thermoelasticity without energy dissipation,” Journal of Elasticity, Vol. 31, No. 3, pp. 189–208, Jun. 1993, https://doi.org/10.1007/bf00044969

Publisher
D. Y. Tzou, “A unified field approach for heat conduction from macro – to micro-scales,” Journal of Heat Transfer, Vol. 117, No. 1, pp. 8–16, Feb. 1995, https://doi.org/10.1115/1.2822329

Publisher
M. A. Ezzat, A. A. El-Bary, and M. A. Fayik, “Fractional fourier law with three-phase lag of thermoelasticity,” Mechanics of Advanced Materials and Structures, Vol. 20, No. 8, pp. 593–602, Sep. 2013, https://doi.org/10.1080/15376494.2011.643280

Publisher
M. A. Ezzat and A. A. El-Bary, “Magneto-thermoelectric viscoelastic materials with memory-dependent derivative involving two-temperature,” International Journal of Applied Electromagnetics and Mechanics, Vol. 50, No. 4, pp. 549–567, Mar. 2016, https://doi.org/10.3233/jae-150131

Publisher
M. A. Ezzat and A. A. El-Bary, “Effects of variable thermal conductivity and fractional order of heat transfer on a perfect conducting infinitely long hollow cylinder,” International Journal of Thermal Sciences, Vol. 108, pp. 62–69, Oct. 2016, https://doi.org/10.1016/j.ijthermalsci.2016.04.020

Publisher
M. A. Ezzat, A. S. El-Karamany, and A. A. El-Bary, “Two-temperature theory in Green-Naghdi thermoelasticity with fractional phase-lag heat transfer,” Microsystem Technologies, Vol. 24, No. 2, pp. 951–961, Feb. 2018, https://doi.org/10.1007/s00542-017-3425-6

Publisher
W. Nowacki, “Dynamical problems of thermodiffusion in solids I,” Bulletin of the Polish Academy of Sciences: Technical Sciences, Vol. 22, pp. 55–64, 1974.

Search CrossRef
W. Nowacki, “Dynamical problems of thermo diffusion in solids II,” Bulletin of the Polish Academy of Sciences: Technical Sciences, Vol. 22, pp. 205–211, 1974.

Search CrossRef
H. H. Sherief, F. A. Hamza, and H. A. Saleh, “The theory of generalized thermoelastic diffusion,” International Journal of Engineering Science, Vol. 42, No. 5-6, pp. 591–608, Mar. 2004, https://doi.org/10.1016/j.ijengsci.2003.05.001

Publisher
M. Aouadi, “Generalized theory of thermoelastic diffusion for anisotropic media,” Journal of Thermal Stresses, Vol. 31, No. 3, pp. 270–285, Feb. 2008, https://doi.org/10.1080/01495730701876742

Publisher
M. A. Ezzat and M. A. Fayik, “Fractional order theory of thermoelastic diffusion,” Journal of Thermal Stresses, Vol. 34, No. 8, pp. 851–872, Aug. 2011, https://doi.org/10.1080/01495739.2011.586274

Publisher
A. S. El-Karamany and M. A. Ezzat, “Thermoelastic diffusion with memory-dependent derivative,” Journal of Thermal Stresses, Vol. 39, No. 9, pp. 1035–1050, Sep. 2016, https://doi.org/10.1080/01495739.2016.1192847

Publisher
C. Li, H. Guo, and X. Tian, “A size-dependent generalized thermoelastic diffusion theory and its application,” Journal of Thermal Stresses, Vol. 40, No. 5, pp. 603–626, May 2017, https://doi.org/10.1080/01495739.2017.1300786

Publisher
A. E. Abouelregal, “Generalized mathematical novel model of thermoelastic diffusion with four phase lags and higher-order time derivative,” The European Physical Journal Plus, Vol. 135, No. 2, pp. 1–21, Feb. 2020, https://doi.org/10.1140/epjp/s13360-020-00282-2

Publisher
R. A. Toupin, “Theories of elasticity with couple-stress,” Archive for Rational Mechanics and Analysis, Vol. 17, No. 2, pp. 85–112, Jan. 1964, https://doi.org/10.1007/bf00253050

Publisher
R. D. Mindlin and N. N. Eshel, “On first strain-gradient theories in linear elasticity,” International Journal of Solids and Structures, Vol. 4, No. 1, pp. 109–124, Jan. 1968, https://doi.org/10.1016/0020-7683(68)90036-x

Publisher
E. C. Aifantis, “On the role of gradients in the localization of deformation and fracture,” International Journal of Engineering Science, Vol. 30, No. 10, pp. 1279–1299, Oct. 1992, https://doi.org/10.1016/0020-7225(92)90141-3

Publisher
D. Ieşan and R. Quintanilla, “On a strain gradient theory of thermoviscoelasticity,” Mechanics Research Communications, Vol. 48, pp. 52–58, Mar. 2013, https://doi.org/10.1016/j.mechrescom.2012.12.003

Publisher
G. Ahmadi and K. Firoozbakhsh, “First strain gradient theory of thermoelasticity,” International Journal of Solids and Structures, Vol. 11, No. 3, pp. 339–345, Mar. 1975, https://doi.org/10.1016/0020-7683(75)90073-6

Publisher
E. C. Aifantis, “Strain gradient interpretation of size effects,” Fracture Scaling, pp. 299–314, 1999, https://doi.org/10.1007/978-94-011-4659-3_16

Publisher
E. C. Aifantis, “Exploring the applicability of gradient elasticity to certain micro/nano reliability problems,” Microsystem Technologies, Vol. 15, No. 1, pp. 109–115, Jan. 2009, https://doi.org/10.1007/s00542-008-0699-8

Publisher
S. Forest, R. Sievert, and E. C. Aifantis, “Strain gradient crystal plasticity: thermomechanical formulations and applications,” Journal of the Mechanical Behavior of Materials, Vol. 13, No. 3-4, pp. 219–232, Aug. 2002, https://doi.org/10.1515/jmbm.2002.13.3-4.219

Publisher
S. Forest and E. C. Aifantis, “Some links between recent gradient thermo-elasto-plasticity theories and the thermomechanics of generalized continua,” International Journal of Solids and Structures, Vol. 47, No. 25-26, pp. 3367–3376, Dec. 2010, https://doi.org/10.1016/j.ijsolstr.2010.07.009

Publisher
D. Ieşan and R. Quintanilla, “Strain gradient theory of chiral Cosserat thermoelasticity without energy dissipation,” Journal of Mathematical Analysis and Applications, Vol. 437, No. 2, pp. 1219–1235, May 2016, https://doi.org/10.1016/j.jmaa.2016.01.058

Publisher
D. Ieşan and R. Quintanilla., “Qualitative properties in strain gradient thermoelasticity with microtemperatures,” Mathematics and Mechanics of Solids, Vol. 23, No. 2, pp. 240–258, 2017, https://doi.org/10.1177/10812865166808

Publisher
M. Aouadi, A. R. E. Dhaba, and A. F. Ghaleb, “Stability aspects in strain gradient theory of thermoelasticity with mass diffusion,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 98, No. 10, pp. 1794–1812, Oct. 2018, https://doi.org/10.1002/zamm.201800043

Publisher
P. Chadwick and I. N. Snedon, “Plane waves in an elastic solid conducting heat,” Journal of the Mechanics and Physics of Solids, Vol. 6, No. 3, pp. 223–230, May 1958, https://doi.org/10.1016/0022-5096(58)90027-9

Publisher
P. Puri, “Plane waves in generalized thermoelasticity,” International Journal of Engineering Science, Vol. 11, No. 7, pp. 735–744, Jul. 1973, https://doi.org/10.1016/0020-7225(73)90003-7

Publisher
V. K. Agarwal, “On plane waves in generalized thermoelasticity,” Acta Mechanica, Vol. 31, No. 3-4, pp. 185–198, Sep. 1979, https://doi.org/10.1007/bf01176847

Publisher
J. N. Sharma, V. Kumar, and S. P. Sud, “Plane harmonic waves in orthorhombic thermoelastic materials,” The Journal of the Acoustical Society of America, Vol. 107, No. 1, pp. 293–305, Jan. 2000, https://doi.org/10.1121/1.428347

Publisher
K. L. Verma and N. Hasebe, “Wave propagation in plates of general anisotropic media in generalized thermoelasticity,” International Journal of Engineering Science, Vol. 39, No. 15, pp. 1739–1763, Oct. 2001, https://doi.org/10.1016/s0020-7225(01)00014-3

Publisher
B. Singh, “Reflection of P and SV waves from free surface of an elastic solid with generalized thermodiffusion,” Journal of Earth System Science, Vol. 114, No. 2, pp. 159–168, Apr. 2005, https://doi.org/10.1007/bf02702017

Publisher
B. Singh, “Reflection of SV waves from the free surface of an elastic solid in generalized thermoelastic diffusion,” Journal of Sound and Vibration, Vol. 291, No. 3-5, pp. 764–778, Apr. 2006, https://doi.org/10.1016/j.jsv.2005.06.035

Publisher
M. I. A. Othman, N. Sarkar, and S. Y. Atwa, “Effect of fractional parameter on plane waves of generalized magneto-thermoelastic diffusion with reference temperature-dependent elastic medium,” Computers and Mathematics with Applications, Vol. 65, No. 7, pp. 1103–1118, Apr. 2013, https://doi.org/10.1016/j.camwa.2013.01.047

Publisher
R. Kumar and V. Gupta, “Plane wave propagation in an anisotropic dual-phase-lag thermoelastic diffusion medium,” Multidiscipline Modeling in Materials and Structures, Vol. 10, No. 4, pp. 562–592, Nov. 2014, https://doi.org/10.1108/mmms-01-2014-0004

Publisher
S. Deswal, S. Kumar, and K. Jain, “Plane wave propagation in a fiber-reinforced diffusive magneto-thermoelastic half space with two-temperature,” Waves in Random and Complex Media, Vol. 32, No. 1, pp. 43–65, Jan. 2022, https://doi.org/10.1080/17455030.2020.1758832

Publisher
B. Singh, “On theory of generalized thermoelastic solids with voids and diffusion,” European Journal of Mechanics – A/Solids, Vol. 30, No. 6, pp. 976–982, Nov. 2011, https://doi.org/10.1016/j.euromechsol.2011.06.007

Publisher

About this article

Received

10 March 2023

Accepted

18 September 2023

Published

23 December 2023

DOI

https://doi.org/10.21595/jets.2023.23268

Keywords

plane wave

phase velocity

attenuation coefficient

thermal and diffusion relaxation times

hyperstress coefficients

Acknowledgements

One of the author Himanshu Singla is thankful for the financial assistance provided by the Council of Scientific and Industrial Research, New Delhi, India, in the form of Senior Research Fellowship through Grant No. 09/135(0792)/2017-EMR-1.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Baljeet Singh has formulated the governing equations for the material under study. Himanshu Singla solved these equations for plane waves. Himanshu Singla also illustrated the numerical results as per numerical plan suggested by Baljeet Singh. Himanshu Singla wrote the whole manuscript and author Baljeet Singh finalized the manuscript after giving inputs in each section of the manuscript.

Conflict of interest

The authors declare that they have no potential conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2023 05 01

Wave propagation in different theories of fractional thermoelasticity

Baljeet Singh

Research article

2022 11 03

Eigen value approach with memory dependant derivative on homogeneous isotropic infinitely extended rotating plate of a finite thickness in absence of heat source

S. Chakraborty, A. Lahiri, B. Das

Research article

2021 11 11

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir, Adiya Dar, Mohamed I. A. Othman

Research article

2021 06 30

Thermal shock problem of a generalized thermoelastic solid sphere affected by mechanical damage and thermal diffusion

Hamdy M. Youssef

B. Singh and H. Singla, “Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory,” Journal of Engineering and Thermal Sciences, Vol. 3, No. 2, pp. 25–40, Dec. 2023, https://doi.org/10.21595/jets.2023.23268

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2023.23268
UR  - https://doi.org/10.21595/jets.2023.23268
TI  - Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory
T2  - Journal of Engineering and Thermal Sciences
AU  - Singh, Baljeet
AU  - Singla, Himanshu
PY  - 2023
DA  - 2023/12/23
PB  - JVE International Ltd.
SP  - 25-40
VL  - 3
IS  - 2
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

 @article{Singh_2023, title={Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory}, volume={3}, ISSN={2669-2465}, url={https://doi.org/10.21595/jets.2023.23268}, DOI={10.21595/jets.2023.23268}, number={2}, journal={Journal of Engineering and Thermal Sciences}, publisher={JVE International Ltd.}, author={Singh, Baljeet and Singla, Himanshu}, year={2023}, month=dec, pages={25–40} }

Copy Bibtex

Copied to clipboard!

[1]B. Singh and H. Singla, “Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory,” Journal of Engineering and Thermal Sciences, vol. 3, no. 2, pp. 25–40, Dec. 2023, doi: 10.21595/jets.2023.23268.

Copy IEEE

Copied to clipboard!

Singh, Baljeet, and Himanshu Singla. “Plane Waves in an Isotropic Thermoelastic Diffusive Material Using Strain Gradient Theory.” Journal of Engineering and Thermal Sciences 3, no. 2 (December 23, 2023): 25–40. https://doi.org/10.21595/jets.2023.23268.

Copy Chicago

Copied to clipboard!

Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Abstract

1. Introduction

2. Governing equations of an isotropic model

3. Specialization in two-dimension

4. Plane wave solution

4.1. In absence of hyperstress coefficients

4.2. In absence of diffusion parameters

4.3. In absence of both diffusion and hyperstress coefficients

5. Numerical results and discussion

6. Conclusions

References

About this article

Related Articles