Eigen value approach with memory dependant derivative on homogeneous isotropic infinitely extended rotating plate of a finite thickness in absence of heat source

1. Introduction

At present, the theory of magneto thermo elasticity which deals with the interactions among the strain, temperature and magnetic field has attracted research personalities not only due to its extensive uses in different fields such as geophysics, for understanding the effects of the earth’s magnetic field, seismic waves, emission of electromagnetic radiations from nuclear devices etc., but also for its applications in different fields such as engineering, high energy The classical coupled thermo elasticity theory of Biot [1] includes the strain-rate gradient in particle accelerators, nuclear reactor’s design etc.

Fourier’s law of heat conduction equation which is transformed to parabolic type diffusion equation predicting infinite speed of propagation. Whereas Cattaneo [4] and Vernotte [18] theory admits the existence of thermal waves which propagate at a finite speed. Tzou [17] made the generalization of thermo elasticity theory with dual phase lag and suggested two different phase lags (DPL) in the Fourier Law of heat conduction in which the first is for the heat flux vector and the second for the temperature gradient. Generalization of thermo elasticity theory with two relaxation time has been made by Green and Lindsay [14] who obtained the explicit versions of the constitutive equations. Ezzat [10] obtained independently these equations and the fundamental solutions for this theory. Ezzat and El-Karamany [12] established the uniqueness and reciprocity theorems for anisotropic media. Ezzat, Othman and El-Karamany [13] introduced a formulation of the boundary integral equation method for generalized thermo elasticity with two relaxation times. The heat conduction equation and all the equations of motion were modified by Green and Lindsay [14] without violating Fourier Law introducing two relaxation time parameters.

Ibrahim A. Abbas et al. [20] [23] discussed fractional order thermoelasticity in infinite medium.

The theory of materials with voids or vacuous pores was first proposed by Jace W.Nunziato and Stephen C. Cowin [21] in 1979 and in a study [22] by Marin Marin, Mohamed I. A. Othman and Ibrahim A. Abbas in which the domain of influence theorem has been extended to cover the generalized thermoelasticity of anisotropic bodies with voids in the context of Lord-Shulman and Green-Lindsay theories where it was proved that for a finite time $t>$ 0 the displacement field, the change in volume fraction and the temperature $T$ generate no disturbance outside a bounded domain .

The G-N theory introduced by Green and Naghdi [15] is based on generalized thermo elasticity where thermal displacement gradient in the constitutive equations is considered.

So we are getting different types of problems which have been solved using different approaches:

Solutions of some problems are not convergent while involving potential functions, whereas they are actually convergent in physical problems.

Because physical problems with given initial and boundary conditions are directly related to considered physical quantities (like stress, strain, heat, temperature etc.) and space variables (displacement, time etc.) but not to potential function. Bahar and Hetnarski [3] discussed the limitations of using potential functions.

Solutions are found by state-space approach where Cayley-Hamilton theorem is applied to the co-efficient matrix of the field variables.

Sometimes solutions are found by Eigen value approach, as in Das and Lahiri [6] in which using the basic equations a vector matrix differential equation is formed and the solutions for the resulting field equations are found by evaluating the Eigen values and Eigen vector of the corresponding coefficient matrix.

The use of memory dependent derivative (MDD) in the Fourier law of heat conduction means that the heat conduction equation and the constitutive equations are modified with kernel function and the time delay in which they can be chosen freely which provides more flexible approaches to describe a material’s practical response.

According to Wang and Li [19], as a new alternative to the fractional order derivative, which has certain features that lead to difficulties when applied to real world problems, the concept of memory-dependent derivative is developed.

For a differentiable function $f\left(t\right)$:

is called the ‘first order memory-dependent derivative’ at t relative to the time delay $\omega >0$ , to denote memory dependence as,$q+\omega D_{\omega }\dot{q}=-k\nabla T$, $q$ being the heat flux relative to the temperature gradient and the kernel function $K\left(t-\eta \right)$ being differentiable at $t$ and $\eta$ can be chosen freely as follows:

where, $a$ and $b$ are constants.

Wang and Li [19] introduced memory-dependent derivative into Lord and Shulman [16] generalized thermoelasticity theory. Recently, Ezzat and Bary [11] also Ezzat, El-Karamany and El-Bary [12, 13] constructed a new generalized thermoelasticity as well as thermo-visco elasticity theory with memory-dependent derivatives.

The present study deals with the concept of “Memory dependent derivative” in heat transfer process in an elastic solid body in absence of heat source in the context of two-phase-lag model of generalized thermo elasticity. Two integral transform such as Laplace transform for time variable and Fourier transform for space variable are employed to the governing equations to formulate vector-matrix differential equation which is then solved by the eigen value approach methodology. The upper and lower surfaces of the plate are shear–stress free whereas a time dependent compression is given to the both surfacesand the entire elastic medium is also rotating with a uniform angular velocity. The inversion of Fourier transformation is carried out using suitable numerical techniques while numerical inversion of Laplace transformation is done by Bellman’s method. Numerical computations for displacement, thermal strain and stress component, temperature distribution are evaluated and presented graphically under influences of different physical parameters.

2. Mathematical model

As discussed in Chakraborty, Das and Lahiri [5], in the fields relating to generalized magneto thermoelasticity with memory-dependent derivative, the displacements and the thermal fields as well as the stress-strain-temperature relations for a linear isotropic medium take the following forms:

The equation of motion:

where, $\mathbf{F}=\mathbf{J}\times \mathbf{B}={\mu }_0\left(\mathbf{J}\times \mathbf{H}\right)$ represents the Lorentz’s force.

The generalized heat conduction equation with memory dependent derivative (MDD) in absence of heat source:

The constitutive stress components are:

The strain displacement components are:

where, electro-magnetic field components are satisfying the Maxwell’s equation which is given by:

Conventionally, we can conclude the following four renowned theories such as:

For classical thermoelasticity (CD) theory [1]: $t_1=t_2=\nu ={\tau }_0=n_0=0$.

For Lord and Shulman (LS) theory [16], generalized thermoelastic formulation with one relaxation time parameter:$t_1=t_2=\nu =0,{\tau }_0>0,n_0=0$, where $\omega ⟶0$ and $D_{\omega }f\left(t\right)⟶\frac{\partial f\left(t\right)}{\partial t}$.

For Green and Lindsay (GL) theory [14], generalized thermoelastic formulation with two relaxation time parameter: $t_1=t_2=n_0=0$, $\nu \ge {\tau }_0>0$, where $\omega ⟶$0 and $D_{\omega }f\left(t\right)⟶\frac{\partial f\left(t\right)}{\partial t}$.

For dual-phase-lag (DPL) theory [17], $t_1>0$, ${\tau }_0>0$, $t_2^2=\frac{1}{2}{\tau }_0^2$, $n_0=\nu =$ 1, where $\omega ⟶0$ and $D_{\omega }f\left(t\right)⟶\frac{\partial f\left(t\right)}{\partial t}$.

Where, $u_i$are displacement components, e is the cubical dilatation, $t$ is time variable, ${\nu }_0$, ${\tau }_0$ are thermal relaxation time parameters, $n_0$ is constant positive number, $t_1$, $t_2$ are dual-phase-lag parameters, $J$ is electric current density vector, $B$is magnetic induction vector, $D$ is electric induction vector, $T$ is absolute thermo dynamical temperature distribution, $T_0$ is reference temperature chosen such that $\left|\frac{T-T_0}{T_0}\right|\ll$ 1, $\rho$is density of the medium, ${\mu }_0$ is magnetic permeability, ${\epsilon }_0$ is electric permeability, ${\delta }_{ij}$ is Kronecker’s delta tensor, ${{\alpha }_0}^2$ is Alfen velocity$=\frac{{\mu }_0{H_0}^2}{\rho }$, $c^2$ is velocity of light$=1/{\mu }_0{\epsilon }_0$, ${c_2}^2$ is velocity of transverse waves$=\mu /\rho$, $C_E$ is Specific heat at constant strain, $\lambda$, $\mu$ are Lame’s Constant, ${\alpha }_T$ is coefficient of linear thermal expansion, $\gamma =\left(3\lambda +2\mu \right){\alpha }_T$, $k$ is coefficient of thermal conductivity, $\epsilon ={\gamma }^2{T}_0/\rho C_E(\lambda +2\mu )$ is the thermal coupling parameter and $\rho$ is density of the material.

3. Formulation of physical problem

Here, the problem is considered for a homogeneous and rotating isotropic infinitely extended thick plate of a finite thickness 2L along the $x$-axis occupying region $R=\left\{\left(x,y,z\right):-L<x<L,-\infty <y<\infty \right\}$, as shown in Fig. 1.

We get the displacement components as $\mathbf{u}=\left(u\left(x,y,t\right),v\left(x,y,t\right),0\right)$ with cubical dilatation, electric and induced magnetic intensities are given by:

Fig. 1Isotropic elastic plate

In absence of body force and internal heat source, we get the equation of motion for the Lorentz’s force as:

The heat conduction equation with MDD is:

and the constitutive stress components are:

We now define the following non-dimensional variables:

Using the non-dimensional variables and for convenience omitting ‘*’ symbol, we can get the non-dimensional form of the Eqs. (5-10) such as:

where:

From now and on the kernel function $K\left(t-\xi \right)$ can be chosen freely as follows:

where, $a$ and $b$ are constants.

4. Solution procedure in laplace and fourier transform domain

The definition of Laplace and Fourier transform of a function $f(x,y,t)$ is given by:

Since, $\mathcal{L}\left[{\int }_{t-\omega }^{t}K(t-\xi )f^{\text{'}}(x,y,\xi )d\xi \right]=\stackrel{-}{f}(x,y,s)\overline{G}(x,\mathrm{\psi },s)$, where, $\overline{G}(x,\mathrm{\psi },s)=\left(1-\frac{2b}{\omega }+\frac{2a^2}{{\omega }^2{s}^2}\right)-e^{-\omega s}\left[\left(1-2b+a^2\right)+\frac{2(a^2-b^2)}{\omega s}+\frac{2a^2}{{\omega }^2{s}^2}\right].$

Taking Laplace and Fourier transform [defined by the Eq. (19)] of the Eqs. (13-15) and omitting the bar symbol, we get:

As in Das, Chakraborty and Lahiri [8] also in Das and Lahiri [7], Eqs. (20-22) can be written as:

where, $\underset{\_}{v}\left(x,\psi ,s\right)={\left[UV\mathrm{\Theta }DUDVD\mathrm{\Theta }\right]}^T$ and the coefficient matrix $\underset{\_}{A}\left(\psi ,s\right)$ is given in the “Appendix”.

For the solution of the vector-matrix differential equation (23), we now apply the method of Eigen value method as in Das, Chakraborty and Lahiri [9] also in Das and Lahiri [8]. The characteristic equation of the matrix $\underset{\_}{A}\left(\psi ,s\right)$ can be written as:

The roots of the characteristic Eq. (24) are: $\lambda =\pm {\lambda }_i$, where, $i=1\left(1\right)3$, which are also the eigenvalues of the matrix $\underset{\_}{A}$ and the corresponding eigenvector $V_i$ corresponding to the eigenvalue ${\lambda }_i$ can be calculated as: $V_i={\left[X\right]}_{\lambda =\pm {\lambda }_i}$, $i=1\left(1\right)3$, where, the values of$m_i’s$, $i=1\left(1\right)5$, are given in Appendix.

Considering the regularity condition at infinity, as in Das, Chakraborty and Lahiri [9] also in Das and Lahiri [8], the general solution of the vector-matrix differential Eq. (23) can be written as:

and Eq. (16) also gives the expressions for stress components such as:

$A_j^{\text{'}}s$ are the arbitrary constants which are determined from the following boundary conditions and the values of $M_{ij}$’s and $x_{ij}$ are given in Appendix.

5. boundary conditions

The boundary conditions are described as follows:

6. Numerical results and discussions

The inversion procedure of Laplace and Fourier transform for the expressions of displacement components, temperature distribution and stress components in space-time domain are very much complicated. For this purpose, we prefer to use an efficient computer programme using suitable programming language for the inversion of two integral transforms. Inversion of Laplace transform for the time variable is carried out numerically using Bellman [2] method whereas the inversion of Fourier transform for the space variable is carried out by Gaussian formula for fixed values of $x$ and $y$.

In the process of numerical calculation, we consider the homogeneous, isotropic, thermally and electrically conducting material medium as that of copper. The material constants (in SI unit) are given by $\lambda =$ 7.76×10¹⁰;$\mu =$3.86×10¹⁰; ${\alpha }_t=$1.78×10^-5; $H_0={10}^7/4\pi$; $L=$ 1, $T_0=$ 293; $C_E=$ 383.1; $\tau =$ 5.5; $\rho =$ 8954; $a=$0.3; $b=$ 0.4.

7. Graphical analysis

Figs. 2 and 3 depict the variations of stress (${\sigma }_{xx})$ versus the space variable ($x$) which is the depth of the plate for fixed values of time $t=t_1$, $t=t_3$ and $t=t_5$ and rotation $\mathrm{\Omega }=$ 10 and 30 respectively. As mentioned earlier for the freely choices of the values of kernel function $K\left(t-\xi \right)$, such as $K\left(t-\xi \right)=1$, $1-\frac{t-\xi }{\omega }$, $1-\left(t-\xi \right)$, ${\left(1-\frac{t-\xi }{\omega }\right)}^2$, it clearly shows that the magnitude of normal stress $\left({\sigma }_{xx}\right)$ vanishes on the upper and lower surfaces of the plate for the same set of values of parameters used in this problem. For the illustration of the stress component $\left({\sigma }_{xx}\right)$ it is also very much important the role of the kernel function $\left(t-\xi \right)$. It is obviously seen that at the lower boundary $\left(x=-L\right)$ of the plate, ${\sigma }_{xx}$ attains maximum for $K\left(t-\xi \right)={\left(1-\frac{t-\xi }{\omega }\right)}^2$ than $\left(1-\frac{t-\xi }{\omega }\right)$ which is also maximum for $K\left(t-\xi \right)=1$ than $K\left(t-\xi \right)=1-\left(t-\xi \right)$. The values of stress $\left({\sigma }_{xx}\right)$ is almost parallel for the fixed values of time $t=t_1$, $t=t_3$ and $t=t_5$ at the middle region of the plate. It is clearly shown from this figures that the stress component $\left({\sigma }_{xx}\right)$ is extensive in nature throughout the whole region $-L\le x\le L$, it also attains the maximum value at $x=$ ± 0.8. These two figures show that the magnitude of stress $\left({\sigma }_{xx}\right)$ sharply increases and also attains the maximum value at the lower boundary of the plate and similarly at the upper boundary, it sharply decreases and finally vanishes.

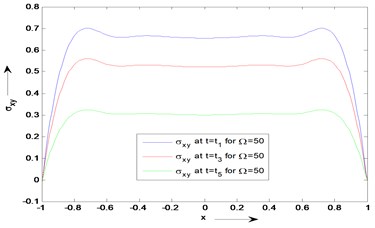
Figs. 4 and 5 give the variations of the shearing stress component $\left({\sigma }_{xy}\right)$ against the depth of the isotropic plate for the same set of values of the parameters used in the MDD model. Here, Fig. 4 is for the value of rotation $\mathrm{\Omega }=$ 10 and Fig. 5 is for $\mathrm{\Omega }=$ 50. It gives the maximum value at $x=$ ± 0.8 and no significant changes in the middle region $(-0.6\le x\le 0.6)$ of the plate.

Figs. 6 and 7 have been plotted to study the variation of stress $\left({\sigma }_{yy}\right)$ against the depth of the plate ($x$). The value of kernel function is taken to be $K\left(t-\xi \right)=1-\frac{t-\xi }{\omega }$, where, $\omega =$ 0.01 and $t=t_1$, $t=t_3$ and $t=t_5$. The qualitative behavior of the stress component $\left({\sigma }_{yy}\right)$ is given by these two figures for different values of rotation ($\mathrm{\Omega }$) and time. The three different values of rotation are taken as $\mathrm{\Omega }=$ 10 and 30 respectively. The stress component $\left({\sigma }_{yy}\right)$ also vanishes at the both lower and upper surfaces of the plate whereas the value of ${\sigma }_{yy}$ increases and decreases at the region of the plate $-1\le x\le -0.4$ and $0.4\le x\le 1$respectively. In the region,$-0.4\le x\le 0.4$, it is almost parallel to each other and significant changes occur.

Fig. 2Distribution of stress component (σxx) versus x at fixed values of time (t) and rotation Ω

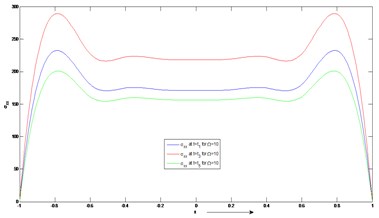
Fig. 3Variation stress component (σxx) versus x for fixed values of time (t) and rotation Ω

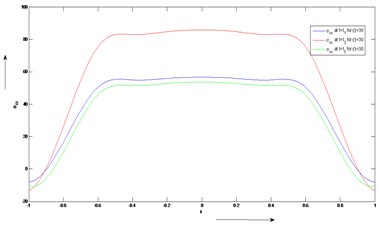
Fig. 4Distribution of stress (σxy) versus x for fixed values of time (t) and rotation Ω

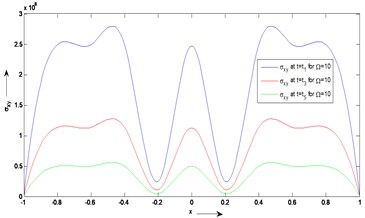
Fig. 5Distribution of stress component (σxy) versus x for fixed values of time (t) and rotation Ω

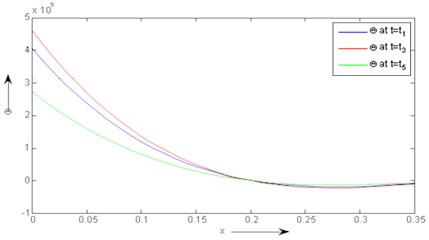
In Fig. 8, the variation of temperature ($\mathrm{\Theta }$) is found for the different choices of the kernel function $K\left(t-\xi \right)$ and the constant values of ‘a’ and ‘b’ also for fixed value of time$t=t_5$. The magnitude of temperature decreases up to $x\le$ 0.2 for different values of kernel function $K\left(t-\xi \right)$.

In Fig. 9, the variation of temperature ($\mathrm{\Theta }$) is found for the different$x$. The magnitude of temperature decreases up to $x\le$ 0.2 and no significant changes occur in the region 0.2 $\le x\le$ 0.35.

Fig. 6Distribution of stress component (σyy) versus x for fixed values of time (t) and rotation Ω

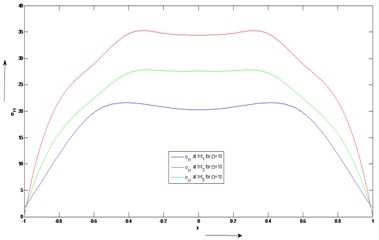
Fig. 7Distribution of stress component (σyy) versus x for fixed values of time (t) and rotation Ω

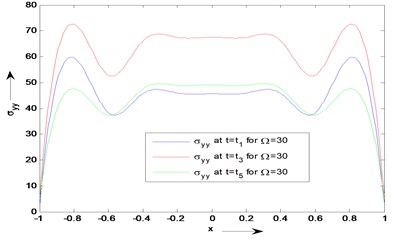
Fig. 8Distribution of temperature Θ versus x for fixed values of kernel function [Kt-ξ]

Fig. 9Distribution of temperature Θ versus x for different time

8. Application

As a new alternative to the Integral Order Calculus and Fractional Order Calculus, having certain features that lead to difficulties when applied to real world fields, such as geophysics, for understanding the effects of the earth’s magnetic field, seismic waves, emission of electromagnetic radiations from nuclear devices, engineering, high energy particle accelerators, nuclear reactor’s designing etc., the concept of Memory-Dependent Derivative was developed. We get more accurate results than the others while using Laplace and Fourier Transformations with time parameters and kernel function with the time-delay parameter.

The results will guide us to slove a 2-D problem with dynamic response of memory-dependent derivatives in homogeneous isotropic magneto-thermoelastic medium with two temperatures which is advantageous to successful applications of memory dependence in heat conduction.

9. Conclusions

The main goal of this article is to introduce a unified new model of generalized magneto thermoelasticity theory with time delay $\omega (>0)$ and the kernel function $K\left(t-\xi \right)$ using the definition for reflection of the memory effect. The form of the kernel function for time delaying memory effect can be chosen freely according to the various applications of the problems. Graphical representations are also explained the necessary importance for the stress distributions in the medium of the plate. Therefore, we can conclude that

1) Thermally and mechanically disturbances are very clear in the neighboring region of the upper and lower surfaces of the plate. No significant disturbance occurred in the middle plane or neighboring region of the middle plane.

2) Significant variations of temperature ($\mathrm{\Theta }$) are observed for different choices of kernel functions. To analyze the time delaying memory effect, it is more fruitful to us to deal with different value of kernel function and it is also more realistic and eventually more compatible to the physical aspects.

3) This problem may be reduced to the simple generalized magneto thermo-elastic model using more conventional Fourier’s law of heat conduction equation defining the values of kernel function as constant and one can compared this result as existing literature.