Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method

Sobamowo, Gbeminiyi M.; Yinusa, Ahmed A.; Dere, Zainab O.; Saheed, Rasheed O.; Gbadamosi, Ridwan O. Ola

doi:10.21595/jets.2022.22807

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 26 November 2022

Check for updates

Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method

Gbeminiyi M. Sobamowo¹

Ahmed A. Yinusa²

Zainab O. Dere³

Rasheed O. Saheed⁴

Ridwan O. Ola Gbadamosi⁵

^{1, 2}Mechanical Engineering Department, University of Lagos, Akoka, Lagos, Nigeria

³Mathematics Department, Florida State University, Tallahassee, Florida, USA

⁴Mechanical Engineering Department, Lagos State University of Science and Technology, Lagos, Nigeria

⁵Mechanical Engineering Department, Lagos State University, Epe Campus, Lagos, Nigeria

Corresponding Author:

Gbeminiyi M. Sobamowo

Cite the article Download PDF

Downloads 361

Abstract

The present investigation is concerned with the development of non-power series solutions for the unsteady state nonlinear thermal model of a radiative-convective fin having temperature-variant thermal conductivity using Laplace transform-Galerkin weighted residual method. In the study, it is demonstrated that the symbolic solutions do not involve a large number of terms, complex mathematical analysis, high computational cost, and time as compared to the power series solutions in previous studies. The solutions allow effective predictions of the extended surface thermal performance over a large domain and time. The results of the non-power series solutions are verified numerically, and very good agreements are established. Parametric studies are carried out with the aid of the symbolic non-power solutions. It is found that as the conductive-convective and conductive-radiative increase, temperature distribution decreases since the rate of heat transfer becomes augmented and hence, the fin thermal efficiency is improved. Additionally, when the thermal conductivity of the fin increases, the temperature distribution in the passive device increases. The temperature increases with time at the different positions in the fin. Following the time histories of the solution, it is shown that unsteady state solutions converge to a steady state as time progresses. It could therefore be stated the developed non-power series analytical solutions provide a good platform for comparison of the nonlinear thermal analyses of fins in thermal systems.

1. Introduction

Indisputably, there are increasing applications of passive devices for heat transfer augmentations and enhancements in thermal and electronic systems [1]. The importance of the passive devices has provoked a large volume of research in literatures. The theoretical investigations of thermal damage problems and heat transfer enhancement by the extended surfaces have attest to the facts that the controlling thermal models of the passive devices are always nonlinear. Consequently, the nonlinear thermal models have been successfully analyzed in the past studies with the aids of approximate analytical, semi-analytical, semi-numerical, and numerical methods. In such previous studies, Jordan et al. [8] adopted optimal linearization method to solve the nonlinear problems in the fin while Kundu and Das [9] utilized Frobenius expanding series method for the analysis of the nonlinear thermal model of the fin. Khani et al. [10] and Amirkolaei and Ganji [11] applied homotopy analysis method. In a further analysis, Aziz and Bouaziz [12], Sobamowo [13], Ganji et al. [14] and Sobamowo et al. [15] employed methods of weighted residual to explore the nonlinear thermal behaviour of fins. In another studies, methods of double decomposition and variation of parameter were used by Sobamowo [16] and Sobamowo et al. [17], respectively to study the thermal characteristics of fins. Also, differential transformation method has been used by some researchers such as Moradi and Ahmadikia [18], Sadri et al. [19], Ndlovu and Moitsheki [20], Mosayebidarchech et al. [21], Ghasemi et al. [22] and Ganji and Dogonchi [23] to predict the heat transfer behaviour in the passive devices. With the help of homotopy perturbation method, Sobamowo et al. [24], Arslanturk [25], Ganji et al. [26] and Hoshyar et al. [27] scrutinized the heat flow in the extended surfaces. However, these studies are for thermal analysis of fin under assumed constant heat transfer coefficient. The cases of heat transfer with variable heat transfer coefficient along the passive device varies has also be investigated [28-35]. Such analysis helps in providing the needed information on the efficiency, effectiveness, and design date of the extended surfaces under various boiling modes [33-44].

Although, as pointed out in the review of the previous studies, there are various approximate analytical and numerical solutions that gained applications in solving the thermal problems [45-52], most of these solutions involve power series. Indubitably, such power series solutions require rigorous solution procedures with inherent large number of terms which are not convenient for use in practice [15]. Therefore, the advantages of generating non-power series analytical solutions to the nonlinear transient problems are very obvious as such solutions allow effective thermal predictions of the extended surface over a large domain and time. Also, the solutions reduce the complex mathematical analysis that gives analytic expressions involving large number terms, high computational cost and time as compared to the power series solutions in previous studies. Hence, the present investigation is concern with the development non-power series analytical solutions for the transient nonlinear thermal model of a radiative-convective fin having temperature-variant thermal conductivity using Laplace transform-Galerkin weighted residual method (LT-GWRM). The developed symbolic solutions are used to examine the impacts of thermal model parameters on performance of fin.

2. Problem formulation

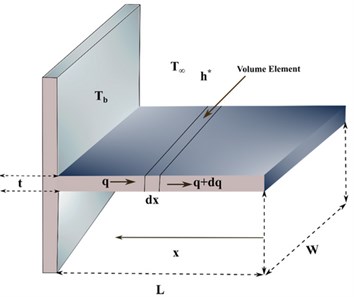
Given a solid rectangular fin having a variable thermal conductivity and exposed to convective-radiative environment at temperature $T_{\infty}$ and heat transfer co-efficient $h$ as in Fig. 1. Assuming that the extended surface is isotropic, homogeneous, and saturated with constant thermo-physical properties. It is taken that the heat transfer is one-dimensional along fin length. The prime surface is in perfectly thermal contact with fin base and there is no heat gain or loss at fin tip.

Fig. 1Schematic of convective-radiative longitudinal fin

Thermal energy equation based on model assumptions is expressed as:

1

\frac{\partial}{\partial x} (k (T^{*}) \frac{\partial T^{*}}{\partial x}) - \frac{P h}{A_{c r}} (T^{*} - T_{\infty}) - \frac{σ P ε}{A_{c r}} ({T^{*}}^{4} - T_{\infty}^{4}) = ρ c_{p} \frac{\partial T^{*}}{\partial t} .

In the case that there is a small temperature difference between the base and the tip of the fin, the term ${T^{*}}^{4}$ in Eq. (3) could be expressed as a linear function of fin temperature as:

2

{T^{*}}^{4} = T_{\infty}^{4} + 4 T_{\infty}^{3} (T^{*} - T_{\infty}) + . . . ≅ 4 T_{\infty}^{3} T^{*} - 3 T_{\infty}^{4} .

Substitution of Eq. (2) into Eq. (1), we have:

3

\frac{\partial}{\partial x} (k (T^{*}) \frac{\partial T^{*}}{\partial x}) - \frac{P h (T^{*} - T_{\infty})}{A_{c r}} - \frac{4 σ ε P T_{\infty}^{3} (T^{*} - T_{\infty})}{A_{c r}} = ρ c_{p} \frac{\partial T^{*}}{\partial t},

where thermal conductivity is expressed as a linear law:

4

k (T^{*}) = k_{b} (1 + γ (T^{*} - T_{\infty})) .

Therefore, Eq. (3) becomes:

5

\frac{\partial}{\partial x} ((1 + γ (T^{*} - T_{\infty})) \frac{\partial T^{*}}{\partial x}) - \frac{h P (T^{*} - T_{\infty})}{k_{b} A_{c r}} - \frac{4 σ ε P T_{\infty}^{3} (T^{*} - T_{\infty})}{k_{b} A_{c r}} = \frac{ρ c_{p}}{k_{b}} \frac{\partial T^{*}}{\partial t} .

The initial condition is:

6

T^{*} = T_{0}, when t = 0, for 0 < x < L,

The boundary conditions for the fin with insulated tip are given as:

7a

\frac{d T^{*}}{d x} = 0, at x = 0, for t > 0,

7b

T^{*} = T_{b}, at x = L, for t > 0 .

Using the following dimensionless parameters of Eq. (8) in Eqs. (5)-(7):

8

X = \frac{x}{L}, θ = \frac{T^{*} - T_{\infty}}{T_{b} - T_{\infty}}, τ = \frac{k_{b} t}{ρ c_{p} L^{2}}, M c = \frac{P h L^{2}}{A_{c r} k_{b}}, N r = \frac{4 σ ε P T_{\infty}^{3} L^{2}}{A_{c r} k_{b}}, β = γ (T_{L} - T_{\infty}),

we arrived at the dimensionless forms of the governing as follows:

9

\frac{\partial}{\partial X} [(1 + β θ) \frac{\partial θ}{\partial X}] - (M c + N r) θ = \frac{\partial θ}{\partial τ} .

Expansion Eq. (9), we have:

10

\frac{\partial^{2} θ}{\partial X^{2}} + β θ \frac{\partial^{2} θ}{\partial X^{2}} + β {(\frac{\partial θ}{\partial X})}^{2} - (M c + N r) θ = \frac{\partial θ}{\partial τ},

and the dimensionless initial is given as:

11

θ = θ_{0}, when τ = 0, for 0 < X < 1,

and the adimensional boundary conditions for the fin are given as:

12a

\frac{\partial θ}{\partial X} = 0, at X = 0, for τ > 0,

12b

θ = 1, at X = 0, for τ > 0,

3. Analytical solutions for the thermal problems using integral transforms

The thermal model in Eq. (10) is nonlinear and such can be solved numerically or by approximate analytical methods. However, the computational methods are approximate methods with inherent high computational cost and time. The approximate solutions involve power series with the rigorous solution procedures and large number of terms are not convenient for use in practice Therefore, the obvious advantages of generating non-power series analytical solutions to the nonlinear problems are very much important and this is given in the present study. Such non-power series solutions allow effective thermal predictions of the extended surface over a large domain and time. Also, the non-power series solutions reduce the complex mathematical analysis that gives analytic expressions involving large number terms, high computational cost and time. Therefore, it very important to find analytical or close form solutions to the thermal problems under investigations. Such symbolic solution will provide better physical insights into the importance of thermo-physical parameters than the numerical methods. In the generation of the analytical solutions to differential equations, the practical significance of transform methods facilitates observation of great many properties and hidden views, of both mathematical and physical interest, which are not yet well known and have not met with proper appreciation. Consequently, using Laplace transforms, analytical solutions are developed for the heat transfer models.

3.1. Laplace transform method (LT)

The LT of function $f (t)$ and corresponding inversion are enumerated as:

13

F (s) = \int_{0}^{\infty} e^{- s t} f (t) d t,

14

f (t) = \frac{1}{2 π i} \int_{s - i \infty}^{s + i \infty} e^{- s t} F (s) d t,

where $s = a + i b$ ( $a, b R$ ) is a complex number.

3.2. Applying LT method to the nonlinear thermal model

Applying Laplace transform to Eq. (10), provides the following solutions:

15

\frac{d^{2} \tilde{θ}}{d X^{2}} + β \tilde{θ} \frac{d^{2} \tilde{θ}}{d X^{2}} + β {(\frac{d \tilde{θ}}{d X})}^{2} - (M c + N r) \tilde{θ} = s \tilde{θ} .

Collecting like terms, we have:

16

\frac{d^{2} \tilde{θ}}{d X^{2}} + β \tilde{θ} \frac{d^{2} \tilde{θ}}{d X^{2}} + β {(\frac{d \tilde{θ}}{d X})}^{2} - (s + M c + N r) \tilde{θ} = 0,

with boundary conditions in Laplace domain are:

17

\begin{array}{l} s > 0, X = 0, \frac{\partial \tilde{θ}}{\partial x} = 0, \\ s > 0, X = 1, \tilde{θ} = \frac{1}{s} . \end{array}

An approximate solution of the form:

18

\tilde{θ} (X, s) = ϕ_{o} (X, s) + Ω ϕ_{1} (X, s) .

Which is given as:

19

\tilde{θ} (X, s) = \frac{c o s h \sqrt{(s + M c + N r)} X}{s c o s h \sqrt{(s + M c + N r)}}

+ Ω [\frac{c o s h [2 \sqrt{(s + M c + N r)}] X}{s c o s h [2 \sqrt{(s + M c + N r)}]} - \frac{c o s h \sqrt{(s + M c + N r)} X}{s c o s h \sqrt{(s + M c + N r)}}] .

Which identically satisfies the boundary conditions of Eq. (17).

Substituting Eq. (18) into Eq. (16), one has:

20

\begin{array}{l} \frac{d^{2} [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X^{2}} + β [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)] \frac{d^{2} [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X^{2}} \\ + β {(\frac{d [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X})}^{2} - (s + N c + N r) [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)] = f (X, s) . \end{array}

According to Galerkin process, the coefficient $Ω$ can be found by defining the condition:

21

\int_{0}^{1} f (X, s) ϕ_{1} (X, s) d X = 0,

22

\int_{0}^{1} \{\frac{d^{2} [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X^{2}} + β [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)] \frac{d^{2} [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X^{2}}

+ β {(\frac{d [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]}{d X})}^{2} - (s + N c + N r) [ϕ_{o} (X, s) + Ω ϕ_{1} (X, s)]\} ϕ_{1} (X, s) d X = 0 .

where:

23

{\tilde{ϕ}}_{o} (X, s) = \frac{c o s h \sqrt{(s + M c + N r)} X}{s c o s h \sqrt{(s + M c + N r)}},

24

{\tilde{ϕ}}_{1} (X, s) = [\frac{c o s h [2 \sqrt{(s + M c + N r)}] X}{s c o s h [2 \sqrt{(s + M c + N r)}]} - \frac{c o s h \sqrt{(s + M c + N r)} X}{s c o s h \sqrt{(s + M c + N r)}}] .

After substitution of Eqs. (23) and (24) into Eq. (22) and integrate, one arrives at:

25

λ_{1} Ω^{2} + λ_{2} Ω + λ_{3} = 0 .

The solution of Eq. (25) is:

26

Ω = \frac{- λ_{2} \pm \sqrt{λ_{2}^{2} - 4 λ_{1} λ_{3}}}{2 λ_{1}},

where:

27a

λ_{1} = \frac{β}{s} [- \frac{2}{3} t a n h^{2} [2 \sqrt{(s + M c + N r)}] - \frac{27}{40} t a n h [2 \sqrt{(s + M c + N r)}]

+ \frac{1}{3} t a n h^{3} [\sqrt{(s + M c + N r)}] + \frac{3}{5} t a n h [\sqrt{(s + M c + N r)}]

+ \frac{177}{40} t a n h [2 \sqrt{(s + M c + N r)}] t a n h^{2} [\sqrt{(s + M c + N r)}]

- 4 t a n h [\sqrt{(s + M c + N r)}] t a n h^{2} [2 \sqrt{(s + M c + N r)}]

- \frac{96}{15} \{\begin{array}{l} t a n h [2 \sqrt{(s + M c + N r)}] \\ \cdot t a n h^{2} [\sqrt{(s + M c + N r)}] \end{array}\} \{\frac{1 - t a n h^{2} [\sqrt{(s + M c + N r)}]}{1 + t a n h^{2} [\sqrt{(s + M c + N r)}]}\}

+ \frac{3}{8} \sqrt{(s + M c + N r)} {\{1 - t a n h^{2} [\sqrt{(s + M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(s + M c + N r)}]}{t a n h^{2} [\sqrt{(s + M c + N r)}]}\}],

27b

λ_{2} = \frac{β}{s} [\frac{14}{5} t a n h [\sqrt{(s + M c + N r)}] - \frac{2}{3} t a n h^{2} [\sqrt{(s + M c + N r)}]

- \frac{31}{40} t a n h [2 \sqrt{(s + M c + N r)}] - \frac{59}{40} t a n h [2 \sqrt{(s + M c + N r)}] t a n h^{2} [\sqrt{(s + M c + N r)}]

- \frac{32}{15} \{\begin{array}{l} t a n h [2 \sqrt{(s + M c + N r)}] \\ \cdot t a n h^{2} [\sqrt{(s + M c + N r + H a)}] \end{array}\} \{\frac{1 - t a n h^{2} [\sqrt{(s + M c + N r)}]}{1 + t a n h^{2} [\sqrt{(s + M c + N r)}]}\}

- \frac{5}{8} \sqrt{(s + M c + N r)} {\{1 - t a n h^{2} [\sqrt{(s + M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(s + M c + N r)}]}{t a n h^{2} [\sqrt{(s + M c + N r)}]}\}]

\times \frac{3}{2 s} [\sqrt{(s + M c + N r)} [t a n h^{2} [2 \sqrt{(s + M c + N r)}] - 1]

- t a n h [2 \sqrt{(s + M c + N r)}] [\frac{1}{3} t a n h^{2} [\sqrt{(s + M c + N r)}] - \frac{1}{2}]],

27c

λ_{3} = \frac{β}{s} [\frac{1}{3} t a n h^{3} [\sqrt{(s + M c + N r)}] - \frac{1}{2} t a n h [\sqrt{(s + M c + N r)}]

+ \frac{1}{4} \sqrt{(s + M c + N r)} {\{1 - t a n h^{2} [\sqrt{(s + M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(s + M c + N r)}]}{t a n h^{2} [\sqrt{(s + M c + N r)}]}\}] .

It is shown from Eq. (26) that $Ω$ has two roots. However, it is established that the appropriate root is the one that gives $β Ω \leq 0$ . The other root gives some kinds of temperature distributions which are physically meaningless.

Also, practical root of $Ω$ which includes Eqs. (27) illustates that the inversion of Eq. (18) will be very difficult to find analytically. Therefore, the inverse Laplace transform of Eq. (18) was found numerically evaluated using Simon’s approach given as:

28

θ (X, τ) = \frac{e^{a_{p} τ}}{τ} [\frac{1}{2} \tilde{θ} (X, a_{p}) + \sum_{n = 1}^{N} R e [\tilde{θ} (X, a_{p} + i \frac{n π}{τ})] (- 1)^{n}],

where optimally, $a_{p} τ =$ 4.7.

For the steady state, $τ \to \infty$ , we have:

29

θ (X) = \frac{c o s h \sqrt{(M c + N r)} X}{c o s h \sqrt{(M c + N r)}} + Ψ [\frac{c o s h [2 \sqrt{(M c + N r)}] X}{c o s h [2 \sqrt{(M c + N r)}]} - \frac{c o s h \sqrt{(M c + N r)} X}{c o s h \sqrt{(M c + N r)}}],

where in the solution of Eq. (31):

30

ξ_{1} Ψ^{2} + ξ_{2} Ψ + ξ_{3} = 0 .

Which gives:

31

Ψ = \frac{- ξ_{2} \pm \sqrt{ξ_{2}^{2} - 4 ξ_{1} ξ_{3}}}{2 ξ_{1}},

where:

32

ξ_{1} = β [- \frac{2}{3} t a n h^{2} [2 \sqrt{(M c + N r)}] - \frac{27}{40} t a n h [2 \sqrt{(M c + N r)}]

+ \frac{1}{3} t a n h^{3} [\sqrt{(M c + N r)}] + \frac{3}{5} t a n h [\sqrt{(M c + N r)}]

+ \frac{177}{40} t a n h [2 \sqrt{(M c + N r)}] t a n h^{2} [\sqrt{(M c + N r)}]

- 4 t a n h [\sqrt{(M c + N r)}] t a n h^{2} [2 \sqrt{(M c + N r)}]

- \frac{96}{15} \{\begin{array}{l} t a n h [2 \sqrt{(M c + N r)}] \\ \cdot t a n h^{2} [\sqrt{(M c + N r)}] \end{array}\} \{\frac{1 - t a n h^{2} [\sqrt{(M c + N r)}]}{1 + t a n h^{2} [\sqrt{(M c + N r)}]}\}

+ \frac{3}{8} \sqrt{(M c + N r)} {\{1 - t a n h^{2} [\sqrt{(M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(M c + N r)}]}{t a n h^{2} [\sqrt{(M c + N r)}]}\}],

33

ξ_{2} = β [\frac{14}{5} t a n h [\sqrt{(M c + N r)}] - \frac{2}{3} t a n h^{2} [\sqrt{(M c + N r)}] - \frac{31}{40} t a n h [2 \sqrt{(M c + N r)}]

- \frac{59}{40} t a n h [2 \sqrt{(M c + N r)}] t a n h^{2} [\sqrt{(M c + N r)}]

- \frac{32}{15} \{\begin{array}{l} t a n h [2 \sqrt{(M c + N r)}] \\ \cdot t a n h^{2} [\sqrt{(M c + N r)}] \end{array}\} \{\frac{1 - t a n h^{2} [\sqrt{(M c + N r)}]}{1 + t a n h^{2} [\sqrt{(M c + N r)}]}\}

- \frac{5}{8} \sqrt{(M c + N r)} {\{1 - t a n h^{2} [\sqrt{(M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(M c + N r)}]}{t a n h^{2} [\sqrt{(M c + N r)}]}\}]

\times \frac{3}{2} [\sqrt{(M c + N r)} [t a n h^{2} [2 \sqrt{(M c + N r)}] - 1]

- t a n h [2 \sqrt{(M c + N r)}] [\frac{1}{3} t a n h^{2} [\sqrt{(M c + N r)}] - \frac{1}{2}]],

34

ξ_{3} = β [\frac{1}{3} t a n h^{3} [\sqrt{(M c + N r)}] - \frac{1}{2} t a n h [\sqrt{(M c + N r)}]

+ \frac{1}{4} \sqrt{(M c + N r)} {\{1 - t a n h^{2} [\sqrt{(M c + N r)}]\}}^{2} \{\frac{t a n h [2 \sqrt{(M c + N r)}]}{t a n h^{2} [\sqrt{(M c + N r)}]}\}] .

Fin efficiency is given for the transient state as:

35

η = \int_{0}^{1} \tilde{θ} (X, s) d X = \frac{t a n h [\sqrt{(s + M c + N r)}]}{s [\sqrt{(s + M c + N r)}]} [1 - Ω \{\frac{t a n h^{2} [\sqrt{(s + M c + N r)}]}{1 + t a n h^{2} [\sqrt{(s + M c + N r)}]}\}] .

While for the steady state as:

36

η = \int_{0}^{1} θ (X) d X = \frac{t a n h [\sqrt{(M c + N r)}]}{[\sqrt{(M c + N r)}]} [1 - Ψ \{\frac{t a n h^{2} [\sqrt{(M c + N r)}]}{1 + t a n h^{2} [\sqrt{(M c + N r)}]}\}] .

Using Laplace transform, the exact analytical solution for the linear thermal model $β$ :

37

1 + \frac{4}{π} \sum_{n = 1}^{\infty} \frac{(- 1)^{n}}{2 n - 1} e^{- \frac{[(2 n - 1)^{2} π^{2} + (M c + N r)] t}{4}} c o s [\frac{(2 n - 1) π X}{2}] .

It is very difficult to provide an explicit exact analytical solution to the nonlinear thermal model in this work. Therefore, the nonlinear model was also solved numerically using Crank-Nicolson finite different method. The finite difference method for the nonlinear thermal model in Eq. (11) is:

38

(\frac{θ_{i + 1}^{n + 1} - 2 θ_{i}^{n + 1} + θ_{i - 1}^{n + 1} + θ_{i + 1}^{n} - 2 θ_{i}^{n} + θ_{i - 1}^{n}}{2 Δ^{2} X})

+ β (θ_{i}^{n}) (\frac{θ_{i + 1}^{n + 1} - 2 θ_{i}^{n + 1} + θ_{i - 1}^{n + 1} + θ_{i + 1}^{n} - 2 θ_{i}^{n} + θ_{i - 1}^{n}}{2 Δ^{2} X})

+ β {(\frac{θ_{i + 1}^{n + 1} - θ_{i - 1}^{n + 1} + θ_{i + 1}^{n} - θ_{i - 1}^{n}}{4 Δ X})}^{2} - (M c + N r) θ_{i}^{n} = (\frac{θ_{i}^{n + 1} - θ_{i}^{n}}{Δ τ}) .

The FDM for the initial condition is:

39

θ_{i}^{o} = 0 .

While FDM for boundary conditions become:

40

\frac{θ_{1}^{n} - θ_{- 1}^{n}}{2 Δ X} = 0 ​ ​ ​ ​ ​ \Rightarrow θ_{1}^{n} = θ_{- 1}^{n}, θ_{M}^{n} = 1 .

4. Results and discussion

The solutions of LT-GWRM are developed and shown in Figs. 2-10. However, Table 1 shows comparison of the results of finite difference method (FDM) and LT-GWRM for the nonlinear thermal models while Figs. 2 presents comparison of nonlinear thermal model results of LT-GWRM with the results of FDM using another set of the model parameters.

Fig. 2Comparison of nonlinear model results of FDM and LT-GWRM

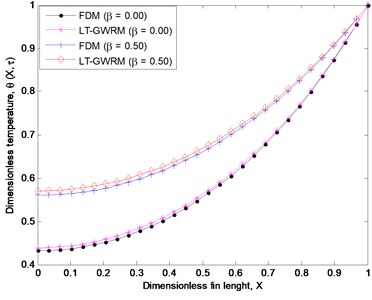
Fig. 3, 4 and 5 illustrate the effects of coductive-convective, condiuctive-radiative and magnetic field parameters on the temperature profiles of the fin, respectively. From the figures, as the coductive-convective, conductive-radiative and magnetic field parameters increase, it is shown that fin thermal distribution decreases. It can be seen in Fig. 3 that the decrease in the temperature of the fin as a result of increase in the conductive-convective parameter reveals that an increase in the heat dissipation capability of the fin or increase in the surface heat loss as the coefficient of the heat transfer increases. It could be stated that when the coefficient of heat transfer increases, it significantly enhances the heat flow from the fin base and the surrounding fluid at the surface of the fin tends to convect more heat away from the fin surface thereby reducing the temperature distribution in the fin and continuous enhance the rate of heat transfer through the fin.

Table 1Comparison of results when β= 0.5

X	FDM	LT-GWRM
0.0000	0.7897	0.7873
0.2000	0.7991	0.7963
0.4000	0.8225	0.8201
0.6000	0.8624	0.8605
0.8000	0.9223	0.9206
1.0000	1.0000	1.0000

In Fig. 4, where it is shown that the fin temperature decreases as the value of conductive-radiative parameter increases. The is because as more heat is released from the surface of the fin through thermal radiation, the intensity of the radiative cooling increases i.e. the fin loses heat to the ambient fluid effectively and consequently, fin temperature drops.

Fig. 3Effects of conductive-convective parameter on fin thermal distribution

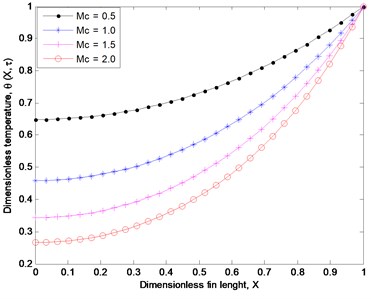
Fig. 4Effects of conductor-radiative parameter on fin thermal distribution

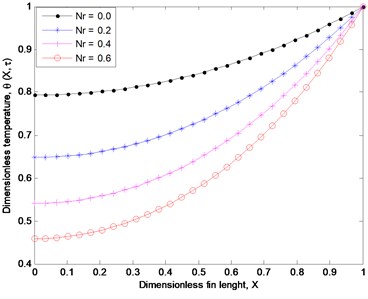
Fig. 5Impacts of thermal conductivity factor on the fin thermal distribution

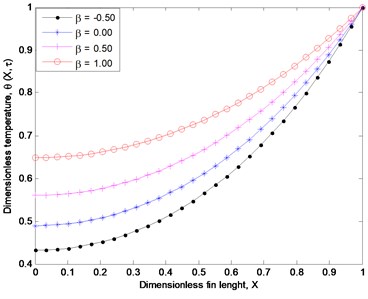
Fig. 6Effects of time on the fin thermal distribution

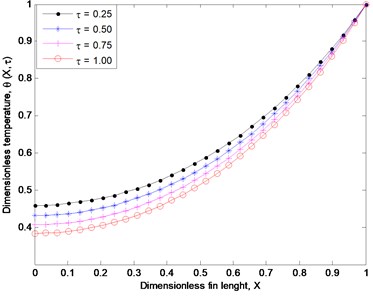
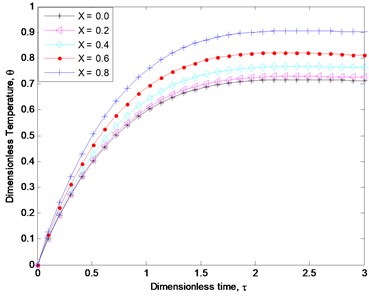
Fig. 5 shows the effect of the fin thermal conductivity on the transient thermal behaviour of the extended surface. The figure shows when the fin thermal conductivity and thermal conductivity gradient increase, the fin temperature increases, the fin temperature increases. This is because, increase in the fin thermal conductivity and the thermal conductivity gradient causes an increase in the local temperature of the fin and makes the heat conducted through the fin increases, thereby the fin heat dissipation capability or surface heat loss to reduce. Moreover, a material of high thermal conductivity tends to store more heat than dissipating it as compared to a material of low thermal conductivity that dissipates heat more easily. It could therefore be said that when a high heat dissipation process is required as in the case compact and miniaturized equipment in thermal system applications such as cooling of electronic systems and devices, it is suggested that a material of relatively low thermal conductivity should be used. Fig. 6 shows the temperature profiles at different times while Fig. 7 illustrates the temperature histories at different positions in the fin. It could be observed that at the different positions in the fin, the temperature increases with an increase in time. The time histories of the solution shows that transient solutions converge to a steady state and the fin tip temperature increases as time progresses.

Fig. 7Temperature history in the fin at various locations in the fin

5. Conclusions

In this paper, with the aid of Laplace transform-Galerkin weighted residual method, non-power series solutions have been developed for the analysis of transient nonlinear thermal behaviour of conductive-radiative-convective fin with varying thermal conductivity. The verifications of the results of the solutions were done by comparing the results of the analytical solutions with the result of a numerical method. It was established that very good agreements were found. Parametric studies in the work showed that the coductive-convective and condiuctive-radiative parameters increase, the fin’s thermal profile reduces while fin’s heat transfer capability is augmented and hence, the fin thermal efficiency is augmented. However, the fin’s thermal profile is enhanced through the ﬁn as value of the thermal conductivity term amplifies. At the different positions in the fin, the temperature grows as the time evolution progresses. The time histories of the solution shows that transient solutions converge to a steady state and the fin tip temperature increases as time progresses. This study serves to provide a good platform of comparison of results for the future works on nonlinear transient thermal analyses of fin. In our further study in the future, we will do a comparative study of two analytical solutions of power and non-power series. Such study will establish a relative advantage of the symbolic solutions over one another.

References

S. Kiwan and M. A. Al-Nimr, “Using porous fins for heat transfer enhancement,” Journal of Heat Transfer, Vol. 123, No. 4, pp. 790–795, Aug. 2001, https://doi.org/10.1115/1.1371922

Publisher
S. Kiwan, “Effect of radiative losses on the heat transfer from porous fins,” International Journal of Thermal Sciences, Vol. 46, No. 10, pp. 1046–1055, Oct. 2007, https://doi.org/10.1016/j.ijthermalsci.2006.11.013

Publisher
S. Kiwan and O. Zeitoun, “Natural convection in a horizontal cylindrical annulus using porous fins,” International Journal of Numerical Methods for Heat and Fluid Flow, Vol. 18, No. 5, pp. 618–634, Jun. 2008, https://doi.org/10.1108/09615530810879747

Publisher
S. Kiwan, “Thermal Analysis of Natural Convection Porous Fins,” Transport in Porous Media, Vol. 67, No. 1, pp. 17–29, Mar. 2007, https://doi.org/10.1007/s11242-006-0010-3

Publisher
R. S. R. Gorla and A. Y. Bakier, “Thermal analysis of natural convection and radiation in porous fins,” International Communications in Heat and Mass Transfer, Vol. 38, No. 5, pp. 638–645, May 2011, https://doi.org/10.1016/j.icheatmasstransfer.2010.12.024

Publisher
B. Kundu, D. Bhanja, and K.-S. Lee, “A model on the basis of analytics for computing maximum heat transfer in porous fins,” International Journal of Heat and Mass Transfer, Vol. 55, No. 25-26, pp. 7611–7622, Dec. 2012, https://doi.org/10.1016/j.ijheatmasstransfer.2012.07.069

Publisher
M. T. Darvishi, R. Gorla, F. Khani, and A. Aziz, “Thermal performance of a porus radial fin with natural convection and radiative heat losses,” Thermal Science, Vol. 19, No. 2, pp. 669–678, 2015, https://doi.org/10.2298/tsci120619149d

Publisher
A. Jordan, S. Khaldi, M. Benmouna, and A. Borucki, “Study of non-linear heat transfer problems,” Revue de Physique Appliquée, Vol. 22, No. 1, pp. 101–105, 1987, https://doi.org/10.1051/rphysap:01987002201010100

Publisher
B. Kundu and P. K. Das, “Performance analysis and optimization of straight taper fins with variable heat transfer coefficient,” International Journal of Heat and Mass Transfer, Vol. 45, No. 24, pp. 4739–4751, Nov. 2002, https://doi.org/10.1016/s0017-9310(02)00189-8

Publisher
F. Khani, M. A. Raji, and H. H. Nejad, “Analytical solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 8, pp. 3327–3338, Aug. 2009, https://doi.org/10.1016/j.cnsns.2009.01.012

Publisher
S. R. Amirkolaei and D. Ganji, “Thermal performance of trapezoidal and rectangular profiles fin with temperature-dependent heat transfer coefficient, thermal conductivity and emissivity,” Indian Journal of Scientific Research (IJSR), Vol. 1, No. 2, pp. 223–229, 2014.

Search CrossRef
A. Aziz and M. N. Bouaziz, “A least squares method for a longitudinal fin with temperature dependent internal heat generation and thermal conductivity,” Energy Conversion and Management, Vol. 52, No. 8-9, pp. 2876–2882, Aug. 2011, https://doi.org/10.1016/j.enconman.2011.04.003

Publisher
M. G. Sobamowo, “Thermal analysis of longitudinal fin with temperature-dependent properties and internal heat generation using Galerkin’s method of weighted residual,” Applied Thermal Engineering, Vol. 99, pp. 1316–1330, Apr. 2016, https://doi.org/10.1016/j.applthermaleng.2015.11.076

Publisher
D. D. Ganji, M. Raghoshay, M. Rahimi, and M. Jafari, “Numerical investigation of fin efficiency and temperature distribution of conductive, convective and radiative straight fins,” International Journal of Recent Research and Applied Studies, pp. 230–237, 2010.

Search CrossRef
M. G. Sobamowo, O. M. Kamiyo, and O. A. Adeleye, “Thermal performance analysis of a natural convection porous fin with temperature-dependent thermal conductivity and internal heat generation,” Thermal Science and Engineering Progress, Vol. 1, pp. 39–52, Mar. 2017, https://doi.org/10.1016/j.tsep.2017.02.007

Publisher
G. Sobamowo, “Thermal performance and optimum design analysis of fin with variable thermal conductivity using double decomposition method,” Journal of Mechanical Engineering and Technology, Vol. 9, No. 1, pp. 1–32, 2017.

Search CrossRef
G. Sobamowo, L. Jayesimi, and J. Femi-Oyetoro, “Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method,” Journal of Applied Mathematics and Computational Mechanics, Vol. 16, No. 3, pp. 85–96, Sep. 2017, https://doi.org/10.17512/jamcm.2017.3.08

Publisher
A. Moradi and H. Ahmadikia, “Analytical solution for different profiles of fin with temperature-dependent thermal conductivity,” Mathematical Problems in Engineering, Vol. 2010, pp. 1–15, 2010, https://doi.org/10.1155/2010/568263

Publisher
S. Sadri, M. R. Raveshi, and S. Amiri, “Efficiency analysis of straight fin with variable heat transfer coefficient and thermal conductivity,” Journal of Mechanical Science and Technology, Vol. 26, No. 4, pp. 1283–1290, Apr. 2012, https://doi.org/10.1007/s12206-012-0202-4

Publisher
P. L. Ndlovu and R. J. Moitsheki, “Analytical solutions for steady heat transfer in longitudinal fins with temperature-dependent properties,” Mathematical Problems in Engineering, Vol. 2013, pp. 1–14, 2013, https://doi.org/10.1155/2013/273052

Publisher
S. Mosayebidorcheh, D. D. Ganji, and M. Farzinpoor, “Approximate solution of the nonlinear heat transfer equation of a fin with the power-law temperature-dependent thermal conductivity and heat transfer coefficient,” Propulsion and Power Research, Vol. 3, No. 1, pp. 41–47, Mar. 2014, https://doi.org/10.1016/j.jppr.2014.01.005

Publisher
S. E. Ghasemi, M. Hatami, and D. D. Ganji, “Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation,” Case Studies in Thermal Engineering, Vol. 4, pp. 1–8, Nov. 2014, https://doi.org/10.1016/j.csite.2014.05.002

Publisher
D. D. Ganji and A. S. Dogonchi, “Analytical investigation of convective heat transfer of a longitudinal fin with temperature – dependent thermal conductivity, heat transfer coefficient and heat generation,” International Journal of Physical Sciences, Vol. 9, No. 21, pp. 466–474, 2014.

Search CrossRef
G. Sobamowo, O. Adeleye, and A. Yinusa, “Analysis of convective-radiative porous fin with temperature-dependent internal heat generation and magnetic field usinghomotopy perturbation method,” Journal of Computational and Applied Mechanics, Vol. 12, No. 2, pp. 127–145, 2017, https://doi.org/10.32973/jcam.2017.009

Publisher
C. Arslanturk, “Optimization of straight fins with a step change in thickness and variable thermal conductivity by homotopy perturbation method,” Journal of Thermal Science and Technology, Vol. 10, pp. 9–19, 2010.

Search CrossRef
D. Ganji, Z. Ganji, and D. Ganji, “Determination of temperature distribution for annular fins with temperature dependent thermal conductivity by HPM,” Thermal Science, Vol. 15, No. suppl. 1, pp. 111–115, 2011, https://doi.org/10.2298/tsci11s1111g

Publisher
H. A. Hoshyar, I. Rahimipetroudi, D. D. Ganji, and A. R. Majidian, “Thermal performance of porous fins with temperature-dependent heat generation via the homotopy perturbation method and collocation method,” Journal of Applied Mathematics and Computational Mechanics, Vol. 14, No. 4, pp. 53–65, Dec. 2015, https://doi.org/10.17512/jamcm.2015.4.06

Publisher
K. Haley and J. Westwater, “Boiling heat transfer from single fins,” Chemical Engineering Science, Vol. 20, p. 711, 1965.

Publisher
F. Lai and Y. Hsu, “Temperature distribution in a fin partially cooled by nucleate boiling,” AIChE Journal, Vol. 13, pp. 817–821, 1967.

Publisher
A. D. Kraus, “Sixty-Five Years of Extended Surface Technology (1922-1987),” Applied Mechanics Reviews, Vol. 41, No. 9, pp. 321–364, Sep. 1988, https://doi.org/10.1115/1.3151910

Publisher
S. P. Liaw and R. H. Yeh, “Fins with temperature dependent surface heat flux-I. Single heat transfer mode,” International Journal of Heat and Mass Transfer, Vol. 37, No. 10, pp. 1509–1515, Jul. 1994, https://doi.org/10.1016/0017-9310(94)90152-x

Publisher
S. P. Liaw and R. H. Yeh, “Fins with temperature dependent surface heat flux-II. Multi-boiling heat transfer,” International Journal of Heat and Mass Transfer, Vol. 37, No. 10, pp. 1517–1524, Jul. 1994, https://doi.org/10.1016/0017-9310(94)90153-8

Publisher
H. C. Ünal, “Temperature distributions in fins with uniform and non-uniform heat generation and non-uniform heat transfer coefficient,” International Journal of Heat and Mass Transfer, Vol. 30, No. 7, pp. 1465–1477, Jul. 1987, https://doi.org/10.1016/0017-9310(87)90178-5

Publisher
H. C. Ünal, “Determination of the temperature distribution in an extended surface with a non-uniform heat transfer coefficient,” International Journal of Heat and Mass Transfer, Vol. 28, No. 12, pp. 2279–2284, Dec. 1985, https://doi.org/10.1016/0017-9310(85)90046-8

Publisher
H. C. Ünal, “A simple method of dimensioning straight fins for nucleate pool boiling,” International Journal of Heat and Mass Transfer, Vol. 29, No. 4, pp. 640–644, Apr. 1986, https://doi.org/10.1016/0017-9310(86)90097-9

Publisher
H. C. Ünal, “An analytic study of boiling heat transfer from a fin,” International Journal of Heat and Mass Transfer, Vol. 30, No. 2, pp. 341–349, Feb. 1987, https://doi.org/10.1016/0017-9310(87)90122-0

Publisher
R. H. Yeh and S. P. Liaw, “An exact solution for thermal characteristics of fins with power-law heat transfer coefficient,” International Communications in Heat and Mass Transfer, Vol. 17, No. 3, pp. 317–330, May 1990, https://doi.org/10.1016/0735-1933(90)90096-3

Publisher
A. K. Sen and S. Trinh, “An exact solution for the rate of heat transfer from a rectangular fin governed by a power law-type temperature dependence,” Journal of Heat Transfer, Vol. 108, No. 2, pp. 457–459, May 1986, https://doi.org/10.1115/1.3246946

Publisher
S. P. Liaw and R. H. Yeh, “Analysis of pool boiling heat transfer on a single cylindrical fin,” Chinese Journal of Mechanical Engineering, Vol. 11, pp. 448–454, 1990.

Search CrossRef
R. H. Yeh and S. P. Liaw, “Theoretical study of a fin subject to various types of heat transfer,” Tatung Journal, Vol. 20, pp. 59–66, 1990.

Search CrossRef
W. W. Lin and D. J. Lee, “Boiling on a straight pin fin,” AIChE Journal, Vol. 42, No. 10, pp. 2721–2728, Oct. 1996, https://doi.org/10.1002/aic.690421004

Publisher
W.-R. Liao, L.-H. Chien, M. Ghalambaz, and W.-M. Yan, “Experimental study of boiling heat transfer in a microchannel with nucleated-shape columnar micro-pin-fins,” International Communications in Heat and Mass Transfer, Vol. 108, p. 104277, Nov. 2019, https://doi.org/10.1016/j.icheatmasstransfer.2019.104277

Publisher
A. Emamifar, H. Moghadasi, M. J. Noroozi, and H. Saffari, “Transient analysis of convective-radiative heat transfer through porous fins with temperature-dependent thermal conductivity and internal heat generation,” Journal of Thermal Engineering, Vol. 8, No. 5, pp. 666–676, Oct. 2022, https://doi.org/10.18186/thermal.1190558

Publisher
W. W. Lin and D. J. Lee, “Boiling on a straight pin fin with variable thermal conductivity,” Heat and Mass Transfer, Vol. 34, No. 5, pp. 381–386, Feb. 1999, https://doi.org/10.1007/s002310050273

Publisher
M. Hatami and D. D. Ganji, “Thermal performance of circular convective-radiative porous fins with different section shapes and materials,” Energy Conversion and Management, Vol. 76, pp. 185–193, Dec. 2013, https://doi.org/10.1016/j.enconman.2013.07.040

Publisher
M. Hatami, G. R. Mehdizadeh Ahangar, D. D. Ganji, and K. Boubaker, “Refrigeration efficiency analysis for fully wet semi-spherical porous fins,” Energy Conversion and Management, Vol. 84, pp. 533–540, Aug. 2014, https://doi.org/10.1016/j.enconman.2014.05.007

Publisher
A. Moradi, T. Hayat, and A. Alsaedi, “Convection-radiation thermal analysis of triangular porous fins with temperature-dependent thermal conductivity by DTM,” Energy Conversion and Management, Vol. 77, pp. 70–77, Jan. 2014, https://doi.org/10.1016/j.enconman.2013.09.016

Publisher
M. Darvishi, R. Gorla, and F. Khani, “Natural convection and radiation in porous fins,” Heat and Mass Transfer, Vol. 38, pp. 638–645, 2013.

Publisher
S. Saedodin and M. Shahbabaei, “Thermal analysis of natural convection in porous fins with homotopy perturbation method (HPM),” Arabian Journal for Science and Engineering, Vol. 38, No. 8, pp. 2227–2231, Aug. 2013, https://doi.org/10.1007/s13369-013-0581-6

Publisher
S. E. Ghasemi, P. Valipour, M. Hatami, and D. D. Ganji, “Heat transfer study on solid and porous convective fins with temperature-dependent heat generation using efficient analytical method,” Journal of Central South University, Vol. 21, No. 12, pp. 4592–4598, Dec. 2014, https://doi.org/10.1007/s11771-014-2465-7

Publisher
Y. Rostamiyan, D. Ganji, R. Petroudi, and K. Nejad, “Analytical investigation of nonlinear model arising in heat transfer through the porous fin,” Thermal Science, Vol. 18, No. 2, pp. 409–417, 2014, https://doi.org/10.2298/tsci111217103r

Publisher
R. Petroudi et al., “Semi-analytical method for solving non-linear equation arising of natural convection porous fin,” Thermal Science, Vol. 16, No. 5, pp. 1303–1308, 2012, https://doi.org/10.2298/tsci1205303p

Publisher
S. Abbasbandy, E. Shivanian, and I. Hashim, “Exact analytical solution of forced convection in a porous-saturated duct,” Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 10, pp. 3981–3989, Oct. 2011, https://doi.org/10.1016/j.cnsns.2011.01.009

Publisher

About this article

Received

13 July 2022

Accepted

08 October 2022

Published

26 November 2022

DOI

https://doi.org/10.21595/jets.2022.22807

Keywords

analytical solution

rectangular fin

temperature-dependent

Laplace transform

Galerkin weighted residual method

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Sobamowo M. Gbeminiyi: formulation of overarching research goals and aims. Development or design of methodology; creation of models. Management and coordination responsibility for the research activity planning and execution. Oversight and leadership responsibility for the research activity planning and execution, mentorship external to the core team. Application of mathematical and computational techniques to analyze the problem. Programming, software development; designing computer programs; implementation of the computer code and supporting algorithms; testing of existing code components.

Yinusa Ahmed Amoo: programming, software development; designing computer programs; implementation of the computer code and supporting algorithms; testing of existing code components.

Dere Zainab Olabisi: preparation, creation and/or presentation of the published work. Provision of study materials, computing resources. Acquisition of the financial support for the project leading to this publication. Conducting a research and investigation process.

Saheed Rasheed Olatunji: preparation, creation and/or presentation of the published work Provision of study materials, computing resources.

Ola-Gbadamosi Ridwan O.: provision of study materials, computing resources. Acquisition of the financial support for the project leading to this publication. Conducting a research and investigation process

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 23

Development and analysis of thermal flow field: a new experimental approach

Arun Kiran Pal

Research article

2023 11 17

Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method

M. G. Sobamowo, H. Berrehal, A. B. Ajayi, O. K. Onanuga, R. O. Fawumi

Research article

2022 10 25

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef, Raafat A. A. Salem

Research article

2021 12 28

Significance of fin tip temperature on the heat transfer rate and thermal efficiency of a convective-radiative rectangular fin with variable thermal conductivity

M. G. Sobamowo, O. A. Adeleye, A. A. Yinusa, M. O. Oyekeye, M. A. Waheed

G. M. Sobamowo, A. A. Yinusa, Z. O. Dere, R. O. Saheed, and R. O. O. Gbadamosi, “Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method,” Journal of Engineering and Thermal Sciences, Vol. 2, No. 2, pp. 84–99, Nov. 2022, https://doi.org/10.21595/jets.2022.22807

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2022.22807
UR  - https://doi.org/10.21595/jets.2022.22807
TI  - Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method
T2  - Journal of Engineering and Thermal Sciences
AU  - Sobamowo, Gbeminiyi M.
AU  - Yinusa, Ahmed A.
AU  - Dere, Zainab O.
AU  - Saheed, Rasheed O.
AU  - Gbadamosi, Ridwan O. Ola
PY  - 2022
DA  - 2022/11/26
PB  - JVE International Ltd.
SP  - 84-99
VL  - 2
IS  - 2
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Sobamowo_2022,
	doi = {10.21595/jets.2022.22807},
	url = {https://doi.org/10.21595/jets.2022.22807},
	year = 2022,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {2},
	number = {2},
	pages = {84--99},
	author = {Gbeminiyi M. Sobamowo and Ahmed A. Yinusa and Zainab O. Dere and Rasheed O. Saheed and Ridwan O. Ola Gbadamosi},
	title = {Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]G. M. Sobamowo, A. A. Yinusa, Z. O. Dere, R. O. Saheed, and R. O. O. Gbadamosi, “Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method,” Journal of Engineering and Thermal Sciences, vol. 2, no. 2, pp. 84–99, Nov. 2022, doi: 10.21595/jets.2022.22807.

Copy IEEE

Copied to clipboard!

Sobamowo, Gbeminiyi M., Ahmed A. Yinusa, Zainab O. Dere, Rasheed O. Saheed, and Ridwan O. Ola Gbadamosi. “Unsteady State Heat Transfer Analysis of a Convective-Radiative Rectangular Fin Using Laplace Transform-Galerkin Weighted Residual Method.” Journal of Engineering and Thermal Sciences 2, no. 2 (November 26, 2022): 84–99. https://doi.org/10.21595/jets.2022.22807.

Copy Chicago

Copied to clipboard!

Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method

Abstract

1. Introduction

2. Problem formulation

3. Analytical solutions for the thermal problems using integral transforms

3.1. Laplace transform method (LT)

3.2. Applying LT method to the nonlinear thermal model

4. Results and discussion

5. Conclusions

References

About this article

Related Articles