Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method

Sobamowo, M. G.; Berrehal, H.; Ajayi, A. B.; Onanuga, O. K.; Fawumi, R. O.

doi:10.21595/msea.2023.22962

Material Science, Engineering and Applications

Browse Journal

Submit article

Published: 17 November 2023

Check for updates

Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method

M. G. Sobamowo¹

H. Berrehal²

A. B. Ajayi³

O. K. Onanuga⁴

R. O. Fawumi⁵

^{1, 3}Department of Mechanical Engineering, University of Lagos, Lagos, Nigeria

²Department of Physics, Exact Sciences Faculty, Constantine 1 University, Constantine, Algeria

⁴Department of Physics, Lagos State University of Science and Technology, Ikorodu, Lagos, Nigeria

⁵Department of Advanced Engineering Management, Sheffield Hallam University, Sheffield, UK

Corresponding Author:

M. G. Sobamowo

Cite the article Download PDF

Downloads 158

Abstract

A study on enhancement of heat transfer in thermal systems by convective-radiative porous fin with temperature-invariant thermal conductivity is presented in this paper using optimal homotopy asymptotic method. The efficacy of the method is displayed through the verification of the results with the previous studies. Also, significance of various parameters of the nonlinear model on the heat transfer enhancement of thermal systems using the solutions presented by the method are discussed. The graphical representation of the thermal behaviour of the extended surfaces is presented for pictorial discussion. The results illustrate that the augmentations of the conductive-radiative, conductive-convective, porosity and magnetic field cause the extended surface temperature to reduce as a result of increased rate of heat flow via the passive device. The graphical illustrations show that the efficiency and effectiveness of the fin is high at low values of the radiative-conductive, convective-conductive, porosity and magnetic field parameters. This study will assist in proper thermal analysis of fins for effective thermal managements of engineering systems.

1. Introduction

For the passive augmentation of the rate of heat transfer in thermal and electronic components, fins are widely used. In practice, the extended surfaces are attached to heat transfer devices and components to facilitate the rate of heat transfer from the prime surface. Further augmentation of the heat transfer has been achieved through the use of porous fins. Such important passive method of heat transfer enhancements has provoked several studies over the past decades. The importance of the extended surfaces has provoked a large volume of research in literatures. The theoretical investigations of thermal damage problems and heat transfer enhancement by the extended surfaces have attest to the facts that the controlling thermal models of the passive devices are always nonlinear. Consequently, the nonlinear thermal models have been successfully analyzed in the past studies with the aids of approximate analytical, semi-analytical, semi-numerical, and numerical methods. In such previous studies, Jordan et al. [8] adopted optimal linearization method to solve the nonlinear problems in the fin while Kundu and Das [9] utilized Frobenius expanding series method for the analysis of the nonlinear thermal model of the fin. Khani et al. [10] and Amirkolaei and Ganji [11] applied homotopy analysis method. In a further analysis, Aziz and Bouaziz [12], Sobamowo [13], Ganji et al. [14] and Sobamowo et al. [15] employed methods of weighted residual to explore the nonlinear thermal behaviour of fins. In another studies, methods of double decomposition and variation of parameter were used by Sobamowo [16] and Sobamowo et al. [17], respectively to study the thermal characteristics of fins. Also, differential transformation method has been used by some researchers such as Moradi and Ahmadikia [18], Sadri et al. [19], Ndlovu and Moitsheki [20], Mosayebidarchech et al. [21], Ghasemi et al. [22] and Ganji and Dogonchi [23] to predict the heat transfer behaviour in the passive devices. With the help of homotopy perturbation method, Sobamowo et al. [24], Arslanturk [25], Ganji et al. [26] and Hoshyar et al. [27] scrutinized the heat flow in the extended surfaces. With the aid of hybrid method of Laplace transformation and Legendre wavelet collocation, Jemiseye et al. [28] presented the transient heat transfer analysis of fin made of functionally graded materials for electronics cooling. Patel and Meher [29] utilized Adomian decomposition Sumudu transform method to study the thermal characteristics of the fin under the influence of magnetic field while Moradi et al. [30] explored homotopy analysis method to analyze the same problem. In another work, Shateri and Salahshour [31] used least-square method for the heat transfer analysis in the longitudinal porous fins with various profiles and multiple nonlinearities. Sobamowo et al. [32] Laplace transform – Exp-function method to develop explicit exact solutions for nonlinear transient thermal models of a porous moving fin. To the best of the authors’ knowledge, optimal homotopy asymptotic method (OHAM) has not been applied to the fin problem. Consequently, in this work, the optimal asymptotic homotopy method is applied to carry out thermal analysis of convective-radiative porous fin with temperature-variant internal heat generation under the influence of magnetic field. Parametric studies are carried out and the results are discussed.

2. Problem formulation

In Fig. 1, it is consideration is given to a porous fin with temperature-invariant thermal properties allowing radiative and convective heat transfer. To thermally describe the behaviour of the passive device, assumptions is made that the heat flow porous medium is filled with fluid of single-phase. The solid portion of the extended surface is homogeneous and isotropic. The fin temperature changes only along its length and the condition of a perfect thermal contact between the prime surface and the fin base is assumed.

Fig. 1Schematic of the convective-radiative longitudinal porous fin [29]

The unidirectional energy model based on the assumptions and with the aid of Darcy’s model is:

1

\frac{d}{d \tilde{x}} (\frac{d \tilde{T}}{d \tilde{x}} + \frac{4 σ}{3 k_{e f f} β_{R}} \frac{d {\tilde{T}}^{4}}{d \tilde{x}}) - \frac{ρ β c_{p} g K}{v k_{e f f} A_{c r}} (\tilde{T} - T_{a})^{2} - \frac{h (1 - ε) P}{k_{e f f} A_{c r}} (\tilde{T} - T_{a})

- \frac{σ P \in}{k_{e f f} A_{c r}} ({\tilde{T}}^{4} - T_{a}^{4}) - \frac{J_{c} \times J_{c}}{σ k_{e f f} A_{c r}} A_{s} = 0 .

Eq. (1) can be expressed as:

2

\frac{d^{2} \tilde{T}}{d {\tilde{x}}^{2}} + \frac{4 σ}{3 k_{e f f} β_{R}} \frac{d}{d \tilde{x}} (\frac{d {\tilde{T}}^{4}}{d \tilde{x}}) - \frac{ρ β c_{p} g K}{v δ k_{e f f}} (\tilde{T} - T_{a})^{2} - \frac{h (1 - ε)}{k_{e f f} δ} (\tilde{T} - T_{a}) - \frac{σ \in}{k_{e f f} δ} ({\tilde{T}}^{4} - T_{a}^{4}) - \frac{J_{c} \times J_{c}}{σ k_{e f f} A_{c r}} A_{s} = 0 .

The boundary conditions are:

3a

\tilde{x} = 0, \frac{d \tilde{T}}{d \tilde{x}} = 0,

3b

\tilde{x} = L, \tilde{T} = T_{b} .

The term $T^{4}$ can be expressed as a linear function of temperature as:

4

{\tilde{T}}^{4} = T_{a}^{4} + 4 T_{a}^{3} (\tilde{T} - T_{a}) + 6 T_{a}^{2} {(\tilde{T} - T_{\infty})}^{2} + . . . ≅ 4 T_{a}^{3} \tilde{T} - 3 T_{a}^{4} .

Substitution of Eq. (6) into Eq. (5), results in:

5

\frac{d^{2} \tilde{T}}{d {\tilde{x}}^{2}} + \frac{16 σ}{3 k_{e f f} β_{R}} \frac{d^{2} \tilde{T}}{d {\tilde{x}}^{2}} - \frac{ρ β c_{p} g K}{v δ k_{e f f}} (\tilde{T} - T_{a})^{2} - \frac{h (1 - ε)}{k_{e f f} δ} (\tilde{T} - T_{a}) - \frac{4 σ T_{a}^{3} \in}{k_{e f f} δ} (\tilde{T} - T_{a}) - \frac{J_{c} \times J_{c}}{σ k_{e f f} A_{c r}} A_{s} = 0 .

It should be noted that:

6

\frac{J_{c} \times J_{c}}{σ} = σ_{m} B_{o}^{2} u^{2} .

Therefore:

7

\frac{d^{2} \tilde{T}}{d {\tilde{x}}^{2}} + \frac{16 σ}{3 k_{e f f} β_{R}} \frac{d^{2} \tilde{T}}{d {\tilde{x}}^{2}} - \frac{ρ β c_{p} g K}{v δ k_{e f f}} (\tilde{T} - T_{a})^{2} - \frac{h (1 - ε)}{k_{e f f} δ} (\tilde{T} - T_{a})

- \frac{σ T_{a}^{3} \in}{k_{e f f} δ} (\tilde{T} - T_{a}) - \frac{σ_{m \tilde{T}} B_{o}^{2} u^{2}}{A_{c r} k_{e f f}} A_{s} (\tilde{T} - T_{a}) = 0 .

The magnetic field is taken to be temperature-dependent since the magnetic field varies temperature.

Using the following nondimensional parameters in Eq. (8) on Eqs. (3) and (7):

8

X = \frac{x}{L}, θ = \frac{T - T_{a}}{T_{b} - T_{a}}, R a = \frac{g β k (T_{b} - T_{\infty}) L}{v α k_{r}}, M^{2} = \frac{h L}{k_{e f f} t},

R d = \frac{4 σ_{s t} T_{\infty}^{3}}{3 β_{R} k_{e f f}}, N r = \frac{4 σ_{s t} L T_{\infty}^{3}}{k_{e f f} t}, H = \frac{σ_{m \tilde{T}} B_{o}^{2} u^{2} A_{s}}{A_{c r} k_{e f f}} .

The following adimensional form of the governing Eq. (1) is developed:

9

\frac{d^{2} θ}{d X^{2}} + 4 R d \frac{d^{2} θ}{d X^{2}} - R a θ^{2} - M^{2} θ - N r θ - H a θ = 0,

and the adimensional boundary conditions:

10a

X = 0, \frac{d θ}{d X} = 0,

10b

X = 1, θ = 1 .

3. Application of optimal asymptotic homotopy method

In this section, application of optimal asymptotic homotopy method to the nonlinear model.

For OHAM (developed by Marinca and Herizanu [33] and [34] and applied in other works [35-40], we choose the linear operators from Eq. (9) in the form:

11

L [θ] = \frac{d^{2} θ}{d X^{2}} .

The initial approximation $θ_{0} (X)$ can be obtain as:

12

\frac{d^{2} θ_{0}}{d X^{2}} = 0,

with the boundary conditions:

13

X = 0, \frac{d θ_{0}}{d X} = 0, X = 1, θ_{0} = 1 .

Last equation has solutions:

14

θ_{0} (X) = 1 .

Nonlinear operators corresponding to Eq. (9) and linear operator given in Eq. (14) is defined by:

15

N [θ] = - α θ^{2} (X) - β θ (X),

where:

α = \frac{R a}{(1 + 4 R d)}, β = \frac{N c (1 - ε) + N r + H}{(1 + 4 R d)} .

By substituting Eq. (14) into Eq. (15), we can obtain the expression of $N [θ_{0} (X)]$ :

16

N [θ_{0} (X)] = - α - β .

If we consider the first-order approximate solution for nonlinear differential Eq. (9):

17

θ (X) = θ_{0} (X) + θ_{1} (X, C_{i}),

where $θ_{1} (X, C_{i})$ are obtained as:

18

\frac{d^{2} θ_{1}}{d X^{2}} = N [θ_{0} (X)] ℏ (X, C_{i}),

with boundary conditions:

19

X = 0, \frac{d θ_{1}}{d X} = 0, X = 1, θ_{1} = 0 .

Note that the convergence of the approximate solution $θ (X)$ depends up on the auxiliary function $ℏ (X, C_{i})$ , we can choose $ℏ (X, C_{i})$ as:

20

ℏ (X, C_{i}) = C_{1} + C_{2} e^{- X} + C_{3} e^{- 2 X} + \dots C_{p} {e^{-}}^{(p - 1) X} .

By solving Eq. (18) with boundary condition Eq. (19), we obtained:

21

θ_{1} (X) = \frac{1}{2} (β - α) \{\frac{2}{9} C_{4} (e^{- 3 X} - e^{- 3}) + \frac{1}{2} C_{3} (e^{- 2 X} - e^{- 2}) + 2 C_{2} (e^{- X} - e^{- 1})

+ (X - 1) (C_{1} X + C_{1} + 2 C_{2} + C_{3} + \frac{2}{3} C_{4})\} .

Finally, the solution in Eq. (22) is obtained through Eqs. (14) and (21):

22

θ (X) = 1 + \frac{1}{2} (β - α) \{\frac{2}{9} C_{4} (e^{- 3 X} - e^{- 3}) + \frac{1}{2} C_{3} (e^{- 2 X} - e^{- 2}) + 2 C_{2} (e^{- X} - e^{- 1})

+ (X - 1) (C_{1} X + C_{1} + 2 C_{2} + C_{3} + \frac{2}{3} C_{4})\},

where $C_{i}$ is unknown parameters which can be obtained with Least-square method (LSM). In our study we choose $p =$ 4. For example, when $R a =$ 0.3, $R d =$ 0.4, $N c =$ 0.3, $N r =$ 0.5, $H =$ 0.6 and ԑ, the values of constants are: $C_{1} =$ –3.034900727, $C_{2} =$ 6.159911506, $C_{3} =$ –6.848991138, $C_{4} =$ 2.590773069.

Substituting these values in Eq. (22), we obtain $θ (X)$ in a series form as follow:

23

θ (X) = 2.652103740 - 2.463964602 e^{- X} + 0.6848991138 e^{- 2 X}

- 0.1151443183 e^{- 3 X} - 1.439594147 X + 0.6069801454 X^{2} .

4. Efficiency of the fin

The fin efficiency is the ratio of the rate of heat transfer rate by the fin to the rate of heat transfer that would be if the entire fin were at the base temperature. Efficiency of the fin is an indication of thermal performance and is given by:

24

η = \frac{\int_{0}^{1} [\frac{ρ c_{p} g K β}{k_{e f f} t v} (T - T_{a})^{2} + \frac{h}{k_{e f f} t} (T - T_{a}) + \frac{4 σ ε T_{a}^{3}}{k_{e f f} t} (T - T_{a}) + \frac{σ B_{o}^{2} u^{2}}{k_{e f f} A_{c r}} (T - T_{a})] d x}{\frac{ρ c_{p} g K β}{k_{e f f} t v} (T_{b} - T_{a})^{2} + \frac{h}{k_{e f f} t} (T_{b} - T_{a}) + \frac{4 σ ε T_{a}^{3}}{k_{e f f} t} (T_{b} - T_{a}) + \frac{σ B_{o}^{2} u^{2}}{k_{e f f} A_{c r}} (T_{b} - T_{a})} .

Using the dimensional parameters in Eq. (17), we arrived at:

25

η = \frac{R a \int_{0}^{1} θ^{2} d X + \{N c (1 - ε) + N r + H\} \int_{0}^{1} θ d X}{R a + N c (1 - ε) + N r + H} .

5. Results and discussion

The OAHM solutions are simulated for the purpose of graphical illustrations, sensitivity and parametric investigations. Table 1 presents the verifications of results of the OAHM, numerical method (NUM) and differential transformation method (DTM). Although, the DTM provides higher accurate results than OAHM as compared to the results of NM. The higher accuracy is due to the large number of terms (18 terms) in the solutions of DTM as compared to the small number of terms (2 terms). This proves that OAHM is a very convenient mathematical method for the analysis of nonlinear fin thermal models. Also, Table 2 shows the comparison of the results of the present study with the results of the other methods in the previous studies as presented by Patel and Meher [29]. From the results in the table, the validity and superiority of the optimal homotopy asymptotic method are established as the method presents better results with the results of the numerical method.

The significance of various parameters of the nonlinear model on the thermal management enhancement of thermal systems using the solutions presented are graphical represented for pictorial discussion in Figs. 2-11. The results illustrate that the augmentations of the conductive-radiative, conductive-convective, porosity and magnetic field cause the extended surface adimensional temperature to reduce as a result of increased rate of heat flow via the passive device. The graphical illustrations show that the efficiency and effectiveness of the fin is high at low values of the radiative-conductive, convective-conductive, porosity and magnetic field parameters.

Table 1Comparative of results methods using OAHM, DTM and NUM for θX when Rd= 0.5, ε= 0.1, Ra= 0.4, Nc= 0.3, Nr= 0.2, H= 0.1

X	NUM [35]	DTM Ordre 18 [35]	OAHM Ordre 1	Difference 1	Difference 2
0.0	0.86349923	0.86349915	0.86349987	0.00000008	0.00000064
0.1	0.86481708	0.86481703	0.86481420	0.00000005	0.00000288
0.2	0.86877626	0.86877619	0.86877319	0.00000007	0.00000307
0.3	0.87539340	0.87539333	0.87539383	0.00000007	0.00000043
0.4	0.88469650	0.88469643	0.88469975	0.00000007	0.00000325
0.5	0.89672509	0.89672504	0.89672757	0.00000005	0.00000248
0.6	0.91153065	0.91153060	0.91152929	0.00000005	0.00000136
0.7	0.92917705	0.92917701	0.92917206	0.00000004	0.00000499
0.8	0.94974120	0.94974116	0.94973660	0.00000004	0.00000460
0.9	0.97331376	0.97331372	0.97331485	0.00000004	0.00000109
1.0	1.00000000	1.00000000	1.00000741	0.00000000	0.00000741
Difference 1 $= │ θ_{N U M} - θ_{D T M} │$ , Difference 2 $= │ θ_{N U M} - θ_{O H A M} │$

Table 2Comparative of the results of methods using OHAM, ADSTM and LSM Nr= 0.3, Nc= 0.4,H= 0.9, Rd= 0.5 and Ra= 0.1

X	NUM	ADSTM [29]	LSM [36]	OAHM
0.0	0.781820729	0.781820594	0.781820569	0.781820657
0.1	0.783904154	0.783904049	0.783904760	0.783904121
0.2	0.790166187	0.790166063	0.790165668	0.790166132
0.3	0.800641805	0.800641676	0.800641589	0.800641734
0.4	0.815389668	0.815389550	0.815389906	0.815389592
0.5	0.834492509	0.834492402	0.834492969	0.834492478
0.6	0.858057690	0.858057590	0.858057970	0.858057623
0.7	0.886217964	0.886217887	0.886217828	0.886217919
0.8	0.919132513	0.919132442	0.919132060	0.919132480
0.9	0.956988020	0.956987943	0.956987665	0.956987985
1.0	1.000000000	1.000000000	1.000000000	1.000000000

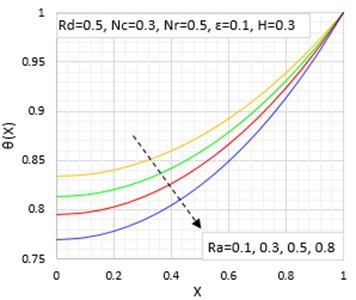
The impacts of convective-conductive, radiative-conductive and porosity parameters on the adimensional temperature distribution in the passive device is graphically illustrated in Fig. 2. The figure shows that as the convection-radiative increases the adimensional temperature in the fin increases. This also means that the local temperature in the extended surface increases as the conduction-convection parameter increases.

Fig. 2Effects of conductive-radiative on the temperature distribution

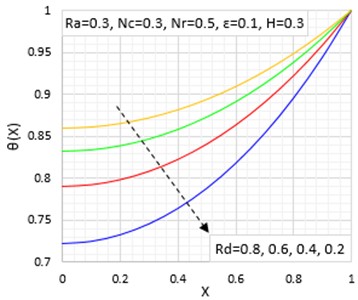
Fig. 3Effects of porous parameter on the temperature distribution

It is presented in Fig. 3 about the impact of porosity on the extended surface temperature behaviour. The graphical illustrations show that the amplification of parameter of porosity (Rayleigh number) causes the passive device temperature to be lessened because of the increased permeability allowed by the fin.

Figs. 4 and 5 display the effects of convective-conductive and radiative-conductive parameters on the fin temperature behaviour. It is shown that the rise of the conductive-radiative, and conductive-convective cause the extended surface adimensional temperature to fall as a result of increased rate of heat flow via the fin. The graphical illustrations show that the efficiency and effectiveness of the fin is high at low values of the radiative-conductive, convective-conductive, porosity and magnetic field parameters.

Fig. 4Effects of convective parameter on the temperature distribution

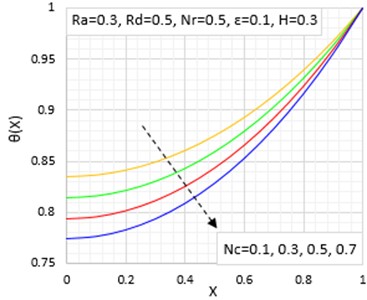
Fig. 5Effects of radiative parameter on the temperature distribution

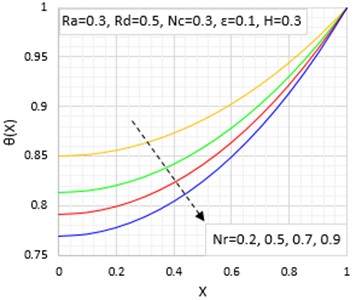
Fig. 6Effects of magnetic parameter on the temperature distribution

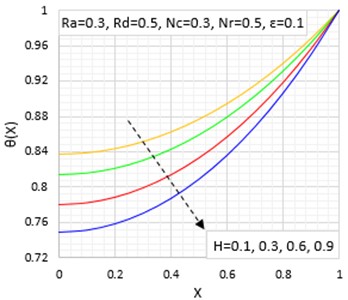
Fig. 7Effects of porosity/void ratio on the temperature distribution

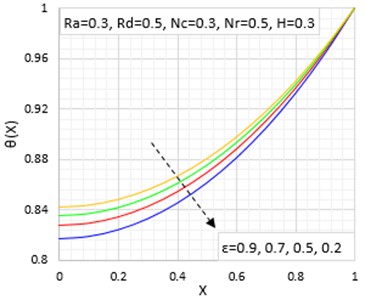
Fig. 6 displays the effect of value of magnetic field or Lorentz force on the fin temperature behaviours. It is illustrated that when the value of the parameter of the magnetic field increase, the passive device temperature decrease. The graphical illustrations show that the efficiency and effectiveness of the fin is high at low values of the magnetic field parameters.

The effects of convective-conductive, radiative-conductive, magnetic field and porous parameters on the thermal efficiency of the fin are presented in Figs. 8, 9 and 10 while the effect of porosity or void ratio on the fin thermal efficiency is shown in Fig. 11. It is shown in the figures that when the convective-conductive, radiative-conductive, porosity and magnetic field parameters rise, the passive device efficiency falls.

Fig. 8Effects of convective parameter on the thermal efficiency

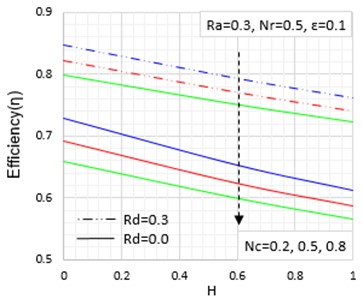
Fig. 9Effects of radiative parameter on the thermal efficiency

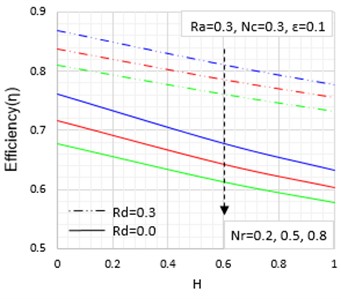
Fig. 10Effects of porous parameter on the temperature distribution

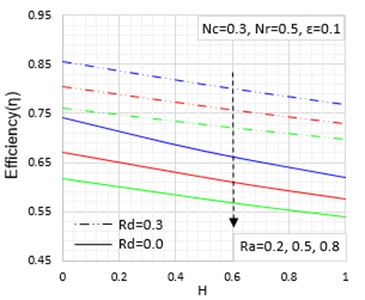
Fig. 11Effects of porosity/void ratio on the temperature distribution

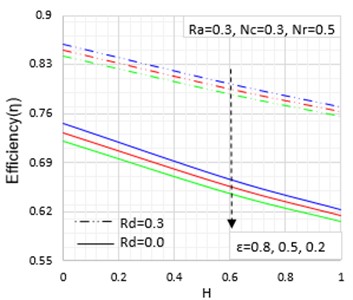
6. Conclusions

In this work, optimal asymptotic homotopy method has been used to investigate the heat transfer characteristics of a convective-radiative porous fin with temperature-invariant thermal conductivity. The effect of various parameters of the nonlinear model on the thermal management enhancement of thermal systems have been explored using the solutions presented by the approximate analytical method. The graphical representations of the thermal behaviour of the extended surfaces have been presented and the results have been discussed. The study has showed that the augmentations of the conductive-radiative, conductive-convective, porosity and magnetic field cause the extended surface temperature to reduce as a result of increased rate of heat flow via the passive device. The graphical illustrations show that the efficiency and effectiveness of the fin is high at low values of the radiative-conductive, convective-conductive, porosity and magnetic field parameters. This study will assist in proper thermal analysis of fins and will help in the passive device design.

References

S. Kiwan and M. A. Al-Nimr, “Using porous fins for heat transfer enhancement,” Journal of Heat Transfer, Vol. 123, No. 4, pp. 790–795, Aug. 2001, https://doi.org/10.1115/1.1371922

Publisher
S. Kiwan, “Effect of radiative losses on the heat transfer from porous fins,” International Journal of Thermal Sciences, Vol. 46, No. 10, pp. 1046–1055, Oct. 2007, https://doi.org/10.1016/j.ijthermalsci.2006.11.013

Publisher
S. Kiwan and O. Zeitoun, “Natural convection in a horizontal cylindrical annulus using porous fins,” International Journal of Numerical Methods for Heat and Fluid Flow, Vol. 18, No. 5, pp. 618–634, Jun. 2008, https://doi.org/10.1108/09615530810879747

Publisher
S. Kiwan, “Thermal analysis of natural convection porous fins,” Transport in Porous Media, Vol. 67, No. 1, pp. 17–29, Mar. 2007, https://doi.org/10.1007/s11242-006-0010-3

Publisher
R. S. R. Gorla and A. Y. Bakier, “Thermal analysis of natural convection and radiation in porous fins,” International Communications in Heat and Mass Transfer, Vol. 38, No. 5, pp. 638–645, May 2011, https://doi.org/10.1016/j.icheatmasstransfer.2010.12.024

Publisher
B. Kundu, D. Bhanja, and K.-S. Lee, “A model on the basis of analytics for computing maximum heat transfer in porous fins,” International Journal of Heat and Mass Transfer, Vol. 55, No. 25-26, pp. 7611–7622, Dec. 2012, https://doi.org/10.1016/j.ijheatmasstransfer.2012.07.069

Publisher
M. T. Darvishi, R. Gorla, F. Khani, and A. Aziz, “Thermal performance of a porus radial fin with natural convection and radiative heat losses,” Thermal Science, Vol. 19, No. 2, pp. 669–678, 2015, https://doi.org/10.2298/tsci120619149d

Publisher
A. Jordan, S. Khaldi, M. Benmouna, and A. Borucki, “Study of non-linear heat transfer problems,” Revue de Physique Appliquée, Vol. 22, No. 1, pp. 101–105, 1987.

Publisher
B. Kundu and P. K. Das, “Performance analysis and optimization of straight taper fins with variable heat transfer coefficient,” International Journal of Heat and Mass Transfer, Vol. 45, No. 24, pp. 4739–4751, Nov. 2002, https://doi.org/10.1016/s0017-9310(02)00189-8

Publisher
F. Khani, M. A. Raji, and H. H. Nejad, “Analytical solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 8, pp. 3327–3338, Aug. 2009, https://doi.org/10.1016/j.cnsns.2009.01.012

Publisher
S. R. Amirkolei and D. D. Ganji, “Thermal performance of a trapezoidal and rectangular profiles fin with temperature-dependent heat transfer coefficient, thermal conductivity and emissivity,” Indian Journal of Scientific Research, Vol. 1, No. 2, pp. 223–229, 2014.

Search CrossRef
A. Aziz and M. N. Bouaziz, “A least squares method for a longitudinal fin with temperature dependent internal heat generation and thermal conductivity,” Energy Conversion and Management, Vol. 52, No. 8-9, pp. 2876–2882, Aug. 2011, https://doi.org/10.1016/j.enconman.2011.04.003

Publisher
M. G. Sobamowo, “Thermal analysis of longitudinal fin with temperature-dependent properties and internal heat generation using Galerkin’s method of weighted residual,” Applied Thermal Engineering, Vol. 99, pp. 1316–1330, Apr. 2016, https://doi.org/10.1016/j.applthermaleng.2015.11.076

Publisher
D. D. Ganji, M. Raghoshay, M. Rahimi, and M. Jafari, “Numerical investigation of fin efficiency and temperature distribution of conductive, convective and radiative straight fins,” IJRRAS, pp. 230–237, 2010.

Search CrossRef
M. G. Sobamowo, O. M. Kamiyo, and O. A. Adeleye, “Thermal performance analysis of a natural convection porous fin with temperature-dependent thermal conductivity and internal heat generation,” Thermal Science and Engineering Progress, Vol. 1, pp. 39–52, Mar. 2017, https://doi.org/10.1016/j.tsep.2017.02.007

Publisher
Gbeminiyi Musibau Sobamowo, “Thermal performance and optimum design analysis of fin with variable thermal conductivity using double decomposition method,” Journal of Mechanical Engineering and Technology (JMET), Vol. 9, No. 1, pp. 1–32, Jun. 2017, https://doi.org/10.2022/jmet.v9i1.1673

Publisher
G. Sobamowo, L. Jayesimi, and J. Femi-Oyetoro, “Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method,” Journal of Applied Mathematics and Computational Mechanics, Vol. 16, No. 3, pp. 85–96, Sep. 2017, https://doi.org/10.17512/jamcm.2017.3.08

Publisher
A. Moradi and H. Ahmadikia, “Analytical solution for different profiles of fin with temperature-dependent thermal conductivity,” Mathematical Problems in Engineering, Vol. 2010, pp. 1–15, 2010, https://doi.org/10.1155/2010/568263

Publisher
S. Sadri, M. R. Raveshi, and S. Amiri, “Efficiency analysis of straight fin with variable heat transfer coefficient and thermal conductivity,” Journal of Mechanical Science and Technology, Vol. 26, No. 4, pp. 1283–1290, Apr. 2012, https://doi.org/10.1007/s12206-012-0202-4

Publisher
P. L. Ndlovu and R. J. Moitsheki, “Analytical solutions for steady heat transfer in longitudinal fins with temperature-dependent properties,” Mathematical Problems in Engineering, Vol. 2013, pp. 1–14, 2013, https://doi.org/10.1155/2013/273052

Publisher
S. Mosayebidorcheh, D. D. Ganji, and M. Farzinpoor, “Approximate solution of the nonlinear heat transfer equation of a fin with the power-law temperature-dependent thermal conductivity and heat transfer coefficient,” Propulsion and Power Research, Vol. 3, No. 1, pp. 41–47, Mar. 2014, https://doi.org/10.1016/j.jppr.2014.01.005

Publisher
S. E. Ghasemi, M. Hatami, and D. D. Ganji, “Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation,” Case Studies in Thermal Engineering, Vol. 4, pp. 1–8, Nov. 2014, https://doi.org/10.1016/j.csite.2014.05.002

Publisher
D. D. Ganji and A. S. Dogonchi, “Analytical investigation of convective heat transfer of a longitudinal fin with temperature-dependent thermal conductivity, heat transfer coefficient and heat generation,” International Journal of Physical Sciences, Vol. 9, No. 21, pp. 466–474, Nov. 2014, https://doi.org/10.5897/ijps2014.4213

Publisher
G. Sobamowo, O. Adeleye, and A. Yinusa, “Analysis of convective-radiative porous fin with temperature-dependent internal heat generation and magnetic field usinghomotopy perturbation method,” Journal of Computational and Applied Mechanics, Vol. 12, No. 2, pp. 127–145, 2017, https://doi.org/10.32973/jcam.2017.009

Publisher
C. Arslanturk, “Performance analysis and optimization of radiating fins with a step change in thickness and variable thermal conductivity by homotopy perturbation method,” Heat and Mass Transfer, Vol. 47, No. 2, pp. 131–138, Feb. 2011, https://doi.org/10.1007/s00231-010-0673-8

Publisher
D. Ganji, Z. Ganji, and D. Ganji, “Determination of temperature distribution for annular fins with temperature dependent thermal conductivity by HPM,” Thermal Science, Vol. 15, No. suppl. 1, pp. 111–115, 2011, https://doi.org/10.2298/tsci11s1111g

Publisher
H. A. Hoshyar, I. Rahimipetroudi, D. D. Ganji, and A. R. Majidian, “Thermal performance of porous fins with temperature-dependent heat generation via the homotopy perturbation method and collocation method,” Journal of Applied Mathematics and Computational Mechanics, Vol. 14, No. 4, pp. 53–65, Dec. 2015, https://doi.org/10.17512/jamcm.2015.4.06

Publisher
A. E. Jemiseye, G. M. Sobamowo, and O. O. Mayowa, “Transient thermal cooling of electronics systems using functional graded fins: hybrid computational analysis,” The Journal of Engineering and Exact Sciences, Vol. 9, No. 4, pp. 15810–1e, May 2023, https://doi.org/10.18540/jcecvl9iss4pp15810-01e

Publisher
T. Patel and R. Meher, “Thermal Analysis of porous fin with uniform magnetic field using Adomian decomposition Sumudu transform method,” Nonlinear Engineering, Vol. 6, No. 3, pp. 191–200, Jan. 2017, https://doi.org/10.1515/nleng-2017-0021

Publisher
A. Moradi, A. P. M. Fallah, T. Hayat, and O. M. Aldossary, “On solution of natural convection and radiation heat transfer problem in a moving porous fin,” Arabian Journal for Science and Engineering, Vol. 39, No. 2, pp. 1303–1312, Feb. 2014, https://doi.org/10.1007/s13369-013-0708-9

Publisher
A. R. Shateri and B. Salahshour, “Comprehensive thermal performance of convection-radiation longitudinal porous fins with various profiles and multiple nonlinearities,” International Journal of Mechanical Sciences, Vol. 136, pp. 252–263, Feb. 2018, https://doi.org/10.1016/j.ijmecsci.2017.12.030

Publisher
G. M. Sobamowo, J. N. Ojuro, O. Onanuga, A. M. O. Siqueira, and J. C. C. Campos, “Explicit exact solutions of nonlinear transient thermal models of a porous moving fin using Laplace transform – exp-function method,” The Journal of Engineering and Exact Sciences, Vol. 9, No. 10, pp. 15972–1e, Sep. 2023, https://doi.org/10.18540/jcecvl9iss10pp15972-01e

Publisher
V. Marinca and N. Herişanu, “Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer,” International Communications in Heat and Mass Transfer, Vol. 35, No. 6, pp. 710–715, Jul. 2008, https://doi.org/10.1016/j.icheatmasstransfer.2008.02.010

Publisher
V. Marinca and N. Herisanu, The Optimal Homotopy Asymptotic Method. Cham, Switzerland: Springer, 2015.

Publisher
H. Berrehal, A. Maougal, T. Hayat, and A. Alsaedi, “On the analytic solution of magnetohydrodynamic (MHD) flow by a moving wedge in porous medium,” Defect and Diffusion Forum, Vol. 389, pp. 128–137, Nov. 2018, https://doi.org/10.4028/www.scientific.net/ddf.389.128

Publisher
F.S. Lai and Y.Y. Hsu, “Temperature distribution in a fin partially cooled by nucleate boiling,” AIChE Journal, Vol. 13, No. 4, pp. 817–821, Jul. 1967, https://doi.org/10.1002/aic.690130444

Publisher
H. A. Hoshyar, D. D. Ganji, and A. Majidian, “Least square method for porous fin in the presence of uniform magnetic field,” Journal of Applied Fluid Mechanics, Vol. 9, No. 2, pp. 661–668, Jan. 2016.

Publisher
H. Berrehal and A. Maougal, “Entropy generation analysis for multi-walled carbon nanotube (MWCNT) suspended nanofluid flow over wedge with thermal radiation and convective boundary condition,” Journal of Mechanical Science and Technology, Vol. 33, No. 1, pp. 459–464, Jan. 2019, https://doi.org/10.1007/s12206-018-1245-y

Publisher
H. Berrehal, F. Mabood, and O. D. Makinde, “Entropy-optimized radiating water/FCNTs nanofluid boundary-layer flow with convective condition,” The European Physical Journal Plus, Vol. 135, No. 7, pp. 1–21, Jul. 2020, https://doi.org/10.1140/epjp/s13360-020-00536-z

Publisher

About this article

Received

28 September 2022

Accepted

13 September 2023

Published

17 November 2023

DOI

https://doi.org/10.21595/msea.2023.22962

Keywords

fins

thermal analysis

optimal homotopy asymptotic method

thermal performance

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Sobamowo M. Gbeminiyi: ideas and formulation of the research. model development. Writing – original draft preparation. writing – review and editing. application of numerical method to analyze the problem.

Hamza Berrehal: Provided solutions, simulated the solutions, Provided data and application of both analytical and numerical methods to analyse the problem.

Arinola Bola Ajayi: verification of the overall replication/reproducibility of results. writing of original draft preparation.

Olutayo Onanuga: writing of the paper – review and editing. verification of the overall replication/reproducibility of results.

Rotimi Fawumi : provisions of resources, verification of the overall replication/reproducibility of results. writing of original draft preparation.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2024 04 21

A ball screw all-round error compensation technology based on novel hybrid deep learning for CNC machine tool

Bo Zhou, Guo-Hua Chen, Jie Mao, Yi Li, Shuai-Wei Zhang

Research article

2022 11 26

Unsteady state heat transfer analysis of a convective-radiative rectangular fin using Laplace Transform-Galerkin weighted residual method

Gbeminiyi M. Sobamowo, Ahmed A. Yinusa, Zainab O. Dere, Rasheed O. Saheed, Ridwan O. Ola Gbadamosi

Research article

2022 10 25

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef, Raafat A. A. Salem

Research article

2021 12 28

Significance of fin tip temperature on the heat transfer rate and thermal efficiency of a convective-radiative rectangular fin with variable thermal conductivity

M. G. Sobamowo, O. A. Adeleye, A. A. Yinusa, M. O. Oyekeye, M. A. Waheed

M. G. Sobamowo, H. Berrehal, A. B. Ajayi, O. K. Onanuga, and R. O. Fawumi, “Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method,” Material Science, Engineering and Applications, Vol. 3, No. 2, pp. 8–20, Nov. 2023, https://doi.org/10.21595/msea.2023.22962

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/msea.2023.22962
UR  - https://doi.org/10.21595/msea.2023.22962
TI  - Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method
T2  - Material Science, Engineering and Applications
AU  - Sobamowo, M. G.
AU  - Berrehal, H.
AU  - Ajayi, A. B.
AU  - Onanuga, O. K.
AU  - Fawumi, R. O.
PY  - 2023
DA  - 2023/11/17
PB  - JVE International Ltd.
SP  - 8-20
VL  - 3
IS  - 2
SN  - 2669-2570
ER  - 

Copy Ris

Copied to clipboard!

 @article{Sobamowo_2023, title={Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method}, volume={3}, ISSN={2669-2570}, url={https://doi.org/10.21595/msea.2023.22962}, DOI={10.21595/msea.2023.22962}, number={2}, journal={Material Science, Engineering and Applications}, publisher={JVE International Ltd.}, author={Sobamowo, M. G. and Berrehal, H. and Ajayi, A. B. and Onanuga, O. K. and Fawumi, R. O.}, year={2023}, month=nov, pages={8–20} }

Copy Bibtex

Copied to clipboard!

[1]M. G. Sobamowo, H. Berrehal, A. B. Ajayi, O. K. Onanuga, and R. O. Fawumi, “Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method,” Material Science, Engineering and Applications, vol. 3, no. 2, pp. 8–20, Nov. 2023, doi: 10.21595/msea.2023.22962.

Copy IEEE

Copied to clipboard!

Sobamowo, M. G., H. Berrehal, A. B. Ajayi, O. K. Onanuga, and R. O. Fawumi. “Thermal Performance Investigation of Porous Fins with Convection and Radiation under the Influence of Magnetic Field Using Optimal Homotopy Asymptotic Method.” Material Science, Engineering and Applications 3, no. 2 (November 17, 2023): 8–20. https://doi.org/10.21595/msea.2023.22962.

Copy Chicago

Copied to clipboard!

Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method

Abstract

1. Introduction

2. Problem formulation

3. Application of optimal asymptotic homotopy method

4. Efficiency of the fin

5. Results and discussion

6. Conclusions

References

About this article

Related Articles