Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction

Odesola, A. S.; Abiala, I. O.; Sobamowo, M. G.; Fenuga, O. J.

doi:10.21595/jets.2022.22815

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 18 October 2022

Check for updates

Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction

A. S. Odesola¹

I. O. Abiala²

M. G. Sobamowo³

O. J. Fenuga⁴

^{1, 2, 3, 4}Department of Mathematics, University of Lagos, Akoka, Lagos, Nigeria

³Department of Mechanical Engineering, University of Lagos, Akoka, Lagos, Nigeria

Corresponding Author:

A. S. Odesola

Cite the article Download PDF

Abstract

This study considered the effect of chemical reaction on transient magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform Heat Source/Sink. The highly nonlinear partial differential equations governing the fluid flow alongside its boundary conditions are formulated and suitable similarity variables are introduced to transform the nonlinear partial differential equations into a set of coupled ordinary differential equations. The results revealed that as the Casson fluid parameter increases, the yield stress reduces thereby reducing the velocity, temperature, and concentration profiles. Magnetic parameter, chemical reaction parameter, stretching ratio parameter and unsteadiness parameter can be used to adjust the fluid velocity, temperature and concentration distributions. The effects of local skin friction coefficients, local Nusselt and Sherwood numbers are also shown and considered using tables. The results revealed that the unsteadiness parameter, Casson fluid parameter and magnetic parameter reduces the momentum boundary layer thickness along $x$ and $y$ direction. The work provides physical insight into the thermo-fluidic flow phenomena of Casson nanofluid under the impacts of magnetic field, internal heat generation and chemical reaction.

Highlights

Transient 3-D MHD flow of heat and mass transfer of a Casson nanofluid is analyzed numerically.
The flow process is numerically analyzed using Finite element analysis.
Effects of non-uniform Heat Source/Sink and chemical reaction on the flow process is considered.
Unsteadiness, Casson fluid and magnetic parameters reduce the momentum boundary layer thickness.
The Nusselt number depreciated, and Sherwood number increases with chemical reaction parameter.
The heat transfer rate is enhanced by varying the value of the magnetic field.
Increase in unsteadiness parameter causes the skin friction, heat and mass transfer rate to increase.

1. Introduction

Chemical reactions with combined heat and mass transfer problems are important in many processes and have gotten a lot of attention in recent years. Heat and mass transfer occur simultaneously in processes such as drying, evaporation at the surface of a water body, energy transfer in a wet cooling tower, the flow in a desert cooler, fruit tree groves, and electric power generation. A chemical reaction between a foreign mass and a fluid occurs in many chemical engineering processes. These processes are used in a variety of industrial applications, including polymer production, ceramics and glassware manufacturing, and food processing [1].

The flow application of non – Newtonian fluids are evident in polymer devolatization and processing, wire and fibre coating, heat exchangers, extrusion process, chemical processing equipment, etc. [2]. Combining heat transfer with the concept of stretching flow is vital in these areas of application. It is well known fact that the fluids appear in industrial and engineering processes are mostly non – Newtonian fluids [3]. The materials that falls into the category of non – Newtonian fluid include sugar solution, colloidal and suspension solution, honey lubricants, etc. the properties of such materials cannot be explored by simple Navier Stokes equations. In the category of non – Newtonian fluid, Casson has a distinctive features [4]. Casson fluids are Jelly, honey, protein, Human blood and fruit juices. Concentrated fluids like sauces, honey, juices, blood, and printing inks can be well described using this model [2]. Non – Newtonian fluid exhibits nonlinear relationship between the shear stress and rate of shear strain [5]. The study of heat transfer in the stretched flow is important because of its extensive application in chemical engineering. Several processes in chemical engineering including metallurgical process and polymer extrusion process involved cooling of molten liquid being stretched into a cooling system, glass fibre and paper production [6]. The quality and final product formation in such processes are dependent on the rate of cooling and stretching [7]. The combined heat and mass transfer problems with chemical reactions are of importance in many processes and therefore have received a considerable attention in recent years. The heat transportation analysis in view of the non – Newtonian fluids have achieved a great significance in technology and science applications like production of synthetic liquids, electro rheological liquid, biological liquids movement, plastic products manufacturing through extrusion, chemical in district (heating/cooling) etc. [8]. It has attracted the attention of new researchers due to their huge range of practical applications in engineering, science and industries [1- 4]. Casson fluid is classified as the most popular non – Newtonian fluids which has several applications in food processing, metallurgy, drilling operations and bio – engineering operations [9]. Human blood, jelly, honey, concentrated fruit juices, tomato sauces are some examples of Casson fluid [1].

Chemical reactions, heat, and mass transfer effects on nonlinear magnetohydrodynamic boundary layer flow over a wedge with a porous medium were investigated by [10] Kandasamy and Palanimani (2007). The effect of magnetohydrodynamic three - dimensional Casson fluid flow past a porous linearly stretching sheet was presented by [4]. In [11], the effects of chemical reactions in a Casson nanofluid hydromagnetic free convection flow induced by a nonlinearly extending sheet immersed in a permeable medium under the influence of convective boundary conditions and thermal radiation using numerical simulations was carried out. The effect of chemical reaction on three-dimensional MHD flow of couple stress Casson fluid past an unsteady stretching surface with convective boundary conditions was investigated by [12]. Investigation of the effects of an exothermic chemical reaction with Arrhenius activation energy, on MHD stagnation point flow of a Casson fluid over a nonlinearly stretching sheet was carried out by [13]. In [4], MHD three – dimensional Casson fluid flow past a porous linearly stretching sheet was carried out. It was obtained that the porosity parameter, Casson fluid parameter and magnetic parameter reduces the momentum boundary layer thickness in both directions. An unsteady MHD Casson fluid flow over a vertical cone and flat plate with non – uniform heat source/sink was studied by [14] and the results indicate that an increase in Casson fluid parameter is found to decelerate the fluid flow by increasing the plastic dynamic viscosity whereas it enhances the shear stress in flow regime. The unsteady magnetohydrodynamic free flow of a Casson fluid over an oscillating vertical plate with constant wall temperature was studied in [15]. The problem of a magnetohydrodynamic three dimensional Casson fluid flow past a porous linearly stretching sheet was investigated in [9]. Three dimensional MHD flow of couple stress Casson fluid past an unsteady stretching surface with the effect of chemical reaction and convective boundary conditions was considered by [12]. The heat and mass transfer of thermally radiating and chemically reacting MHD micropolar fluid flow past a permeable stretching sheet in a porous medium was studied by [16].] ethe Soret – Dufour characteristics in mixed convective radiated Casson fluid flow by exponentially heated surface was studied by [8], the result signifies the characteristics of temperature corresponding to convective and radiation values. This work therefore examines the numerical solution of transient MHD three-dimensional heat and mass transfer of a Casson nanofluid over a stretching sheet through a porous medium using Finite Element Method (FEM).

2. Mathematical model of the problem

We consider a transient, three-dimensional, heat and mass transfer, viscous incompressible, laminar, MHD boundary layer flow analysis of a Casson – nanofluid over an inclined stretching sheet in porous media was considered, as shown in Fig. 1. The fluid flow is caused by the multidirectional stretching of the sheet moving in its own plane with having surface velocities $u = \frac{a x}{1 - c t} + γ \frac{\partial u}{\partial z}$ , $v = \frac{b y}{1 - c t} + γ \frac{\partial v}{\partial z}$ and $w = 0$ , where $a$ , $b$ (stretching rates) are positive constants. The fluid has no lateral motion as $z \to \infty$ . Influences of Brownian and thermophoretic diffusion are considered in the transport equations. Physical properties of the fluid are assumed to be constant. The velocity components of $x$ , $y$ and $z$ are $u$ , $v$ and $w$ respectively. $T_{w}$ and $T_{\infty}$ are convective surface temperature and ambient temperature and $C_{w}$ and $C_{\infty}$ are the concentration of the fluid at the surface of the sheet and ambient concentration respectively.

Fig. 1Physical model and coordinate system

The constitutive equation of state for an isotropic and incompressible Casson fluid is as follows [17-18]:

1

τ_{i j} = \{\begin{array}{l} 2 (μ_{B} + \frac{P_{z}}{\sqrt{2 π}}) e_{i j}, π > π_{c}, \\ 2 (μ_{B} + \frac{P_{z}}{\sqrt{2 π_{c}}}) e_{i j}, π < π_{c}, \end{array}

$w$ here $τ_{i j}$ is the $(i, j)$ th component of the stress tensor, $μ_{B}$ is the plastic dynamic viscosity of the non-Newtonian fluid, $P_{z}$ is the yield stress of the fluid, $π$ is the product of the component of deformation rate with itself $(π = e_{i j}, e_{i j})$ , $e_{i j}$ is the component of deformation rate, $π_{c}$ is the critical value of product based on non-Newtonian model, $β = μ_{B} \frac{\sqrt{2 π_{c}}}{P_{z}}$ is the Casson parameter. Under the above assumptions. Using the Oberbeck Boussinesq and boundary layer approximations, the governing equations describing the continuity, momentum, energy and concentration for the three – dimensional transient flow problem are can be written in Cartesian coordinate is given by [17]:

2

\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,

3

\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} = (1 + \frac{1}{β}) \frac{μ_{n f}}{ρ_{n f}} \frac{\partial^{2} u}{\partial z^{2}} - \frac{σ_{n f} B_{0}^{2}}{ρ_{n f}} u - \frac{μ_{n f}}{ρ_{n f}} \frac{1}{K} u,

4

\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} = (1 + \frac{1}{β}) \frac{μ_{n f}}{ρ_{n f}} \frac{\partial^{2} v}{\partial z^{2}} - \frac{σ_{n f} B_{0}^{2}}{ρ_{n f}} v - \frac{μ_{n f}}{ρ_{n f}} \frac{1}{K} v,

5

\begin{array}{l} \frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} + w \frac{\partial T}{\partial z} = k_{n f} \frac{\partial^{2} T}{\partial z^{2}} - \frac{1}{ρ C_{ρ}} \frac{\partial q_{r}}{\partial z} + \frac{μ_{n f}}{(ρ C_{ρ})} [{(\frac{\partial u}{\partial z})}^{2} + {(\frac{\partial v}{\partial z})}^{2}] + \frac{σ_{n f} B_{0}^{2}}{ρ_{n f}} u^{2} \\ + τ \{D_{B} (\frac{\partial T}{\partial z} \frac{\partial C}{\partial z}) + \frac{D_{T}}{T_{\infty}} {(\frac{\partial T}{\partial z})}^{2}\} + \frac{Q}{ρ C_{ρ}} (T - T_{\infty}) + q^{'''}, \end{array}

6

\frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} + w \frac{\partial C}{\partial z} = D_{B} \frac{\partial^{2} C}{\partial z^{2}} + \frac{D_{T}}{T_{\infty}} \frac{\partial^{2} T}{\partial z^{2}} - K_{0} (C - C_{\infty}) .

The associated boundary conditions are as follows:

7

\begin{array}{l} u = \frac{a x}{1 - c t} + γ \frac{\partial u}{\partial z}, v = \frac{b y}{1 - c t} + γ \frac{\partial v}{\partial z}, w = 0, - k \frac{\partial T}{\partial z} = n_{f} (T_{f} - T), \\ - D_{B} \frac{\partial C}{\partial z} = n_{s} (C_{s} - C), z = 0, u \to 0, v \to 0, T \to T_{\infty}, C \to C_{\infty}, z \to \infty, \end{array}

where $n_{f}$ is the convective heat transfer coefficient, $n_{s}$ is the convective mass transfer coefficient $T_{f}$ and $C_{s}$ are the convective fluid temperature and concentration below the moving sheet:

7a

ρ_{n f} = ρ_{f} (1 - ϕ) + ρ_{S} ϕ,

7b

{(ρ C_{p})}_{n f} = {(ρ C_{p})}_{f} (1 - ϕ) (ρ C_{p}) ϕ .

Employing the Roseland diffusion approximation, the radiative heat flux $q_{r}$ is given by:

7c

q_{r} = \frac{- 4 σ^{*}}{3 k^{*}} \frac{\partial T^{4}}{\partial z},

where $σ^{*}$ represents the Stefan – Boltzmann constant, $k^{*}$ denotes the Rosseland mean absorption coefficient. The temperature difference within the flow are assumed to be sufficiently small so that $T^{4}$ , may be expressed as a linear function of $T$ , and can be expanded by using Taylor’s series about $T_{\infty}$ , as follows:

T^{4} = T_{\infty}^{4} + 4 T_{\infty}^{3} (T - T_{\infty}) + 6 T_{\infty}^{2} {(T - T_{\infty})}^{2} + \dots,

and neglecting the higher order terms beyond the first degree in $(T - T_{\infty})$ , we get:

7d

T^{4} ≅ 4 T_{\infty}^{3} T - 3 T_{\infty}^{4},

as used by other researchers such as [19-22].

Substituting Eq. (7d) into Eq. (7c), we have:

7e

\frac{\partial q_{r}}{\partial z} = \frac{- 16 σ^{*}}{3 k^{*}} T_{\infty}^{3} \frac{a}{v_{f}} (T_{w} - T_{\infty}) θ^{''} (η) .

The non – uniform heat generation/absorption $q'''$ in Eq. (5), as used by [23] is expressed as:

7f

q^{'''} = \frac{k_{n f} U_{w}}{x v_{f}} [A^{*} (T_{w} - T_{\infty}) f^{'} (η) + B^{*} (T - T_{\infty})],

7g

ρ_{n f} = ρ_{f} (1 - ϕ) + ρ_{S} ϕ,

7h

{(ρ C_{p})}_{n f} = {(ρ C_{p})}_{f} (1 - ϕ) (ρ C_{p}) ϕ,

7i

σ_{n f} = σ_{f} [1 + \frac{3 \{\frac{σ_{S}}{σ_{f}} - ϕ\}}{\{\frac{σ_{S}}{σ_{f}} + 2\} ϕ - \{\frac{σ_{S}}{σ_{f}} - 1\} ϕ}],

7j

μ_{n f} = \frac{μ_{f}}{{(1 - ϕ)}^{2.5}},

7k

k_{n f} = k_{f} [\frac{k_{S} - 2 k_{f} - 2 ϕ (k_{f} - k_{S})}{k_{S} - 2 K_{f} + ϕ (k_{f} - k_{S})}] .

Finding solution to the set of Eqs. (2-6), following similarity variables are introduced as given by [24]:

8

u = \frac{a x f' (η)}{1 - c t}, v = \frac{b y g' (η)}{1 - c t}, w = - \sqrt{(\frac{a v_{f}}{1 - c t})} [f (η) + s g (η)],

η = z \sqrt{\frac{a}{(1 - c t) v_{f}}}, C = C_{\infty} + (C_{w} - C_{\infty}) h (η), T = T_{\infty} + (T_{w} - T_{\infty}) θ (η),

where $θ (η)$ is the dimensionless temperature and $h (η)$ is the dimensionless concentration:

9

a f' (η) + a g' (η) - a f' (η) - a g' (η) = 0 .

The above Eq. (9) satisfies the continuity equation in Eq. (2).

The dimensional governing Eqs. (3-6) and the associated boundary conditions Eqs. (7) take the non – dimensional form:

10

(1 + \frac{1}{β}) f''' + [f + s g] f'' - {(f^{'})}^{2} - [λ + M + K_{1}] f' + G r θ + G s h = 0,

11

(1 + \frac{1}{β}) g''' + [f + s g] g'' (η) - s {(g^{'})}^{2} - [λ + M + K_{1}] g' = 0,

12

\begin{array}{l} (1 + \frac{4 R a}{3}) θ'' + P r [f + s g] θ' + (1 + \frac{1}{β}) P r [E c_{x} {(f'')}^{2} + E c_{y} {(g'')}^{2}] \\ + M P r [E c_{x} {(f')}^{2} + E c_{y} {(g')}^{2}] + N b θ' h' + N t ({(θ^{'})}^{2}) + δ P r θ + [A^{*} f^{'} + B^{*} θ] = 0, \end{array}

13

h'' + S c (f + s g) h' + S r θ'' - S c C r h = 0 .

And the boundary conditions are:

14

f = 0, g = 0, f^{'} = 1 + γ f^{''}, θ^{'} = - B_{i t} (1 - θ), h^{'} = - B_{i c} (1 - h),

g^{'} = 1 + γ g^{''}, at η = 0,

15

f^{'} \to 0, g^{'} \to 0, θ^{'} \to 0, h^{'} \to 0, at η \to \infty,

where $B_{i t} = \frac{v_{f}}{k} {(\frac{v_{f}}{a})}^{1 / 2}$ , $B_{i c} = \frac{n_{s}}{D_{B}} {(\frac{v_{f}}{a})}^{1 / 2}$ are thermal and the solutal Biot Numbers respectively.

The non – dimensional variables are:

R a = \frac{4 σ^{*} T_{\infty}^{3} (1 - c t)}{k^{*} k_{n f}}, δ = \frac{Q (1 - c t)}{{(ρ C_{p})}_{n f} a}, E c_{x} = \frac{a^{2} x^{2}}{{(ρ C_{p})}_{n f} (T_{w} - T_{\infty}) {(1 - c t)}^{2}},

P r = \frac{{(ρ C_{p})}_{n f} v_{f}}{k_{n f}}, E c_{y} = \frac{b^{2} y^{2}}{{(ρ C_{p})}_{n f} (T_{w} - T_{\infty}) {(1 - c t)}^{2}}, N b = \frac{τ D_{B} (C_{w} - C_{\infty})}{k_{n f}},

N t = \frac{τ D_{T} (T_{w} - T_{\infty})}{T_{\infty} k_{n f}}, G s = \frac{g_{n f} β_{C}}{a^{2} x} (C_{w} - C_{\infty}) {(1 - c t)}^{2}, M = \frac{σ_{n f} B_{0}^{2} (1 - c t)}{a ρ_{n f}},

K_{1} = \frac{v_{f}}{a K}, G r = \frac{g_{n f} β_{T}}{a^{2} x} (T_{w} - T_{\infty}) {(1 - c t)}^{2}, F r = \frac{C_{b} x}{\sqrt{K_{d}}}, λ = \frac{c}{a}, s = \frac{b}{a} .

The local skin friction coefficients, the Nusselt number, which denotes the rate of heat transfer at the surface of the sheet, and the Sherwood number, which denotes the rate of mass transfer at the surface of the sheet, are the physical quantities of engineering interest considered in this problem. The following are the definitions for these quantities:

16

C_{f x} = \frac{τ_{w x}}{{(ρ C_{p})}_{n f} u_{w}^{2}}, C_{f y} = \frac{τ_{w y}}{{(ρ C_{p})}_{n f} v_{w}^{2}},

τ_{w x} = μ (1 + \frac{1}{β}) {(\frac{\partial u}{\partial z})}_{z = 0}, τ_{w y} = μ (1 + \frac{1}{β}) (\frac{\partial v}{\partial z}) {}_{z = 0},

17

N u_{x} = \frac{x q_{w}}{k (T_{w} - T_{\infty})}, S h_{x} = \frac{x_{q m}}{D_{B} (C_{w} - C_{\infty})},

18

q {}_{w} = - k (1 + \frac{4 R a}{3}) {(\frac{\partial T}{\partial z})}_{z \to 0}, q_{m} = - D_{B} {(\frac{\partial C}{\partial z})}_{z \to 0},

where $τ_{w x}$ and $τ_{w y}$ are the wall shear stress along $x$ and $y$ – directions respectively $q_{w}$ and $q_{m}$ are the heat flux and mass flux at the surface respectively. Applying similarity variables into Eqs. (16-18), the following are obtained:

19

C_{f x} R e^{\frac{1}{2}} = (1 + \frac{1}{β}) f^{''} (0), C_{f y} R e^{\frac{1}{2}} = (1 + \frac{1}{β}) g^{''} (0),

20

N u_{x} R e^{\frac{1}{2}} = - (1 + \frac{4 R}{3}) θ^{'} (0), S h_{x} R e^{\frac{1}{2}} = - h^{'} (0),

where $R e = \frac{u_{w} x}{v_{f}}$ is the local Reynolds number based on the stretching velocity.

3. Method of solution

According to [22], the exact solution for the set of nonlinear differential equations alongside its boundary conditions are not possible and thus we employ a numerical method known as finite element method (FEM). This method has been applied by various researchers [25-28].

The Garlekin global finite element model of the equations for the $i$ th element thus formed is given in matrix form as follows:

21

[\begin{array}{l} [K^{11}] & [K^{12}] & [K^{13}] & [K^{14}] & [K^{15}] & [K^{16}] \\ [K^{21}] & [K^{22}] & [K^{23}] & [K^{24}] & [K^{25}] & [K^{26}] \\ [K^{31}] & [K^{32}] & [K^{33}] & [K^{34}] & [K^{35}] & [K^{36}] \\ [K^{41}] & [K^{42}] & [K^{43}] & [K^{44}] & [K^{45}] & [K^{46}] \\ [K^{51}] & [K^{52}] & [K^{53}] & [K^{54}] & [K^{55}] & [K^{56}] \\ [K^{61}] & [K^{62}] & [K^{63}] & [K^{64}] & [K^{65}] & [K^{66}] \end{array}] \{\begin{array}{l} f^{(e)} \\ r^{(e)} \\ g^{(e)} \\ t^{(e)} \\ θ^{(e)} \\ h^{(e)} \end{array}\} = \{\begin{array}{l} S^{1} \\ S^{2} \\ S^{3} \\ S^{4} \\ S^{5} \\ S^{6} \end{array}\},

where $[K {}^{m n}]$ , $\{f^{(e)}\}$ , $\{r^{(e)}\}$ , $\{g^{(e)}\}$ , $\{t^{(e)}\}$ , $\{θ^{(e)}\}$ , $\{h^{(e)}\}$ and $\{S^{m}\}$ , { $m, n =$ 1,2,…,6} is the set of matrices defined as follows with ${[K {}^{m n}]}_{3 \times 3}$ , ${[S^{m}]}_{2 \times 1}$ , { $m, n =$ 1,2,…, 6} defined as follows:

K^{11} = \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N'}^{(e)}] d η, K^{12} = - \int_{η_{E}}^{η_{E + 1}} {[N^{(e)}]}^{T} [{N'}^{(e)}] d η, K^{13} = K^{14} = K^{15} = K^{16} = 0,

K^{21} = K^{22} = K^{25} = K^{26} = 0, K^{23} = \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η,

K^{24} = - \int_{η_{E}}^{η_{E + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η, K^{31} = K^{33} = K^{34} = 0,

\begin{array}{l} K^{32} = - (1 + \frac{1}{β}) \{\int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N'}^{(e)}] d η\} + \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [{N'}^{(e)}] [N^{(e)}] [N^{(e)}] (f^{(e)} + s g^{(e)})] d η \\ - \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}] (λ + M + K_{1})] d η - \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}] [N^{(e)}]] d η, \end{array}

K^{35} = G r \int_{η_{E}}^{η_{E + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η, K_{i j}^{36} = G s \int_{η_{E}}^{η_{E + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η,

K^{41} = K^{42} = K^{43} = K^{45} = K^{46} = 0

\begin{array}{l} K^{44} = - (1 + \frac{1}{β}) \{\int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N'}^{(e)}] [{N'}^{(e)}] d η\} \\ + \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [{N'}^{(e)}] [N^{(e)}] [{N'}^{(e)}] [N^{(e)}] (f^{(e)} + s g^{(e)})] d η \\ - \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}] (λ + M + K_{1})] d η - s \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}] [N^{(e)}]] d η, \end{array}

K^{51} = K^{53} = K^{56} = 0

K^{52} = (M P r) \int_{η_{e}}^{η_{e + 1}} E c_{x} {[N^{(e)}]}^{T} [N^{(e)}] d η

+ A^{*} \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η + P r E c_{x} (1 + \frac{1}{β}) \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η,

K^{54} = (M P r) \int_{η_{e}}^{η_{e + 1}} E c_{y} {[N^{(e)}]}^{T} [N^{(e)}] d η + P r E c_{y} (1 + \frac{1}{β}) \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [N^{(e)}] d η,

K_{i j}^{55} = - (1 + \frac{4 R a}{3}) \{\int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N^{'}}^{(e)}] [{N^{'}}^{(e)}] d η\}

+ P r \int_{η_{e}}^{η_{e + 1}} ({[N^{(e)}]}^{T} [N^{(e)}] [N^{(e)}] (f^{(e)} + s g^{(e)}) d η)

+ (δ P r + N t + B^{*}) \int_{}^{} {[N^{(e)}]}^{T} [N^{(e)}] d η,

K^{61} = K^{62} = K^{63} = K^{64} = 0, K^{65} = - \int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N^{'}}^{(e)}] [{N^{'}}^{(e)}] d η,

K^{66} = - \{\int_{η_{e}}^{η_{e + 1}} {[N^{(e)}]}^{T} [{N^{'}}^{(e)}] [{N^{'}}^{(e)}] d η\}

+ S c \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}] [{N'}^{(e)}]] (f^{(e)} + s g^{(e)}) d η + S c C r \int_{η_{e}}^{η_{e + 1}} [{[N^{(e)}]}^{T} [N^{(e)}]] d η,

S^{1} = S^{2} = 0, S^{3} = - (1 + \frac{1}{β}) \{{({[N^{(e)}]}^{T} [{N^{'}}^{(e)}])|}_{η_{e}}^{η_{e + 1}}\},

S^{4} = - (1 + \frac{1}{β}) \{{({[N^{(e)}]}^{T} [N^{(e)}])|}_{η_{e}}^{η_{e + 1}}\}, S^{5} = - (1 + \frac{4 R a}{3}) \{{({[N^{(e)}]}^{T} [{N^{'}}^{(e)}] [N^{(e)}])|}_{η_{e}}^{η_{e + 1}}\},

S^{6} = \{{({[N^{(e)}]}^{T} [N^{(e)}] [{N'}^{(e)}] [{N'}^{(e)}])|}_{η_{e}}^{η_{e + 1}}\} + S r \{{({[N^{(e)}]}^{T} [N^{(e)}] [{N'}^{(e)}])|}_{η_{e}}^{η_{e + 1}}\} .

The element matrix given by Eq. (21) is of the order 18×18 and the whole domain is divided into a set of equations a matrix of order 9606×9606 is obtained. The system of equations obtained is nonlinear and therefore an iterative scheme (Gauss - Siedel method of successive relaxation) is used for solving it. After the imposition of the boundary conditions, the system of equations left is solved. Once the convergence criterion $\sum |Θ_{i}^{t} - Θ_{i}^{t - 1}| \leq 1 0^{- 4}$ is satisfied, where $Θ$ stand for either $f$ , $r$ , $g$ , $m$ , $θ$ , $h$ and $t$ represents the iterative step, the iterative process is terminated.

4. Results and discussion

The simulations of the developed numerical solutions are presented in this section. Table 1 presents the values of the surface skin friction, Nusselt number and Sherwood number obtained for different variations of the governing parameters are tabulated. Casson fluid parameter is seen to increase in $x$ direction and decrease in $y$ direction. Magnetic parameter shows an opposite behaviour that is it decreases in both directions. The rate heat transfer and mass transfer are observed to increase for increasing values of Casson and Magnetic field parameters. Also, it is observed that as the chemical reaction parameter increases the surface skin fiction increases in $x$ and decreases in $y$ direction. The Nusselt number and Sherwood number are enhanced by various values of the observed parameters enhanced. The table shows that increasing Prandtl number increase the local Nusselt number and decreases the Sherwood number.

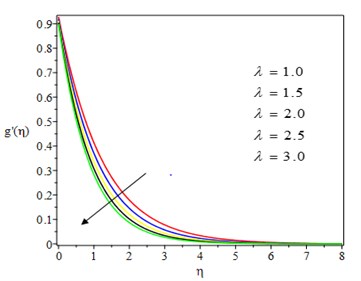
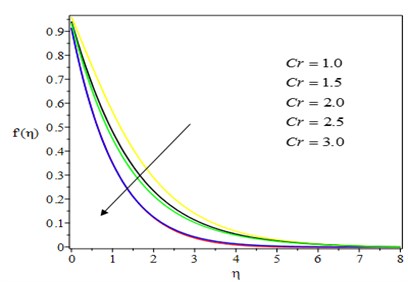
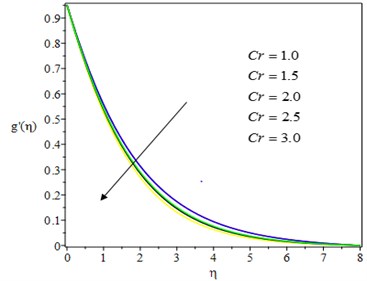
Fig. 2 show the effect of Casson parameter on the fluid velocities, $f' (η)$ and $g' (η)$ , in $x$ and $y$ directions. It can be seen that asCasson parameter increases, the two velocities diminish due to the suppressing nature of the non – Newtonian nature of the fluid. This is also because as the Casson parameter is increased, the yield stress decreases, reducing the thickness of the momentum boundary layer. The effect of the unsteadiness parameter on the velocity profile is shown in Fig. 3. As the unsteadiness parameter increases, the fluid flow is met with more resistance, resulting in lower fluid velocities. The effect of the chemical reaction parameter on velocity profiles in both directions is depicted in Fig. 4. As the chemical reaction parameter is increased, the velocity profiles decrease. This is because the destructive chemical reaction reduces the thickness of the concentration boundary layer, which causes the concentration buoyancy effects to increase, causing the chemical reaction to increase and the fluid velocity to decrease. The effect of Casson parameter on the temperature profile is shown in Fig. 5. Increasing the value of Casson parameter causes the thermal boundary layer thickness to increase. The effect of a chemical reaction parameter on the temperature profile is shown in Fig. 6. As can be seen, as the chemical reaction parameter is increased, the temperature profile rises. This is because chemical energy is effectively converted to thermal energy, which warms the fluid and raises the temperature profile.

Fig. 2Effect of Casson parameter on velocity profile

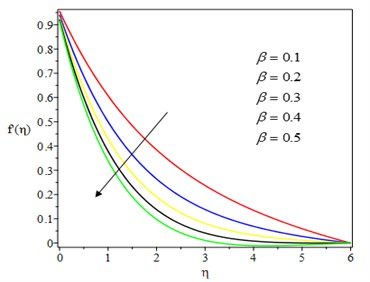
a) $x$ – direction

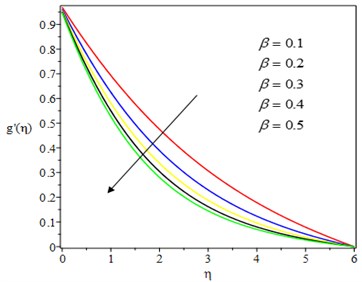
b) $y$ – direction

Fig. 3Effect of unsteadiness parameter on velocity profile

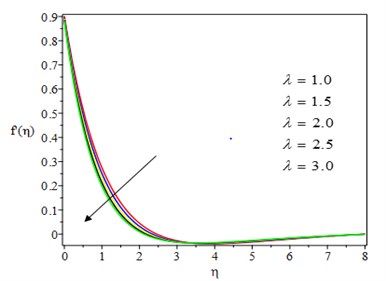
a) $x$ – direction

b) $y$ – direction

Fig. 4Effect of chemical reaction parameter on velocity profile

a) $x$ – direction

b) $y$ – direction

The temperature profile decreases as the unsteadiness parameter increases, as shown in Fig. 7. The reason for this is that as the rate of heat loss by the fluid increases, so does the unsteadiness parameter. In practice, as the unsteadiness parameter rises, the thermal boundary layer shrinks, causing the fluid temperature to plummet. The effect of Casson parameter on the concentration profile is shown in Fig. 8. The concentration boundary layer thickness is reduced as the Casson parameter is increased. Physically, increasing the Casson parameter causes a rise in the viscosity of the fluid, which causes the fluid to slow down and saturate the nanoparticles near the stretching sheet. Fig. 9 depicts the effect of the chemical reaction parameter on the concentration profile. With a higher value of the chemical reaction parameter, the concentration profile is heavily influenced and decelerated. This is because destructive chemical reactions prevent diffusion, lowering the concentration profile.

Fig. 5Effect of Casson parameter on the temperature profile

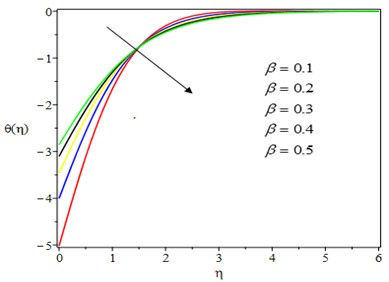
Fig. 6Effect of chemical reaction parameter on the temperature profile

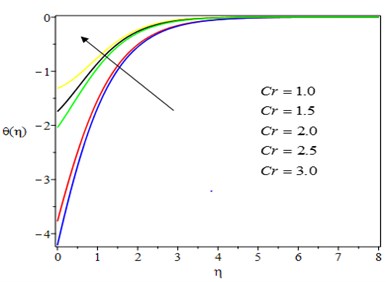
Fig. 7Effect of unsteadiness parameter on temperature profile

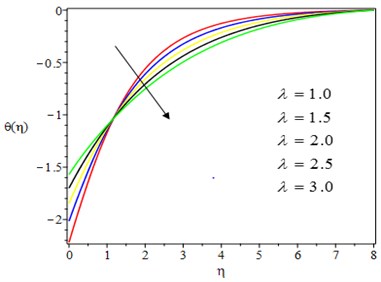
Fig. 8Effect of Casson parameter on the concentration profile

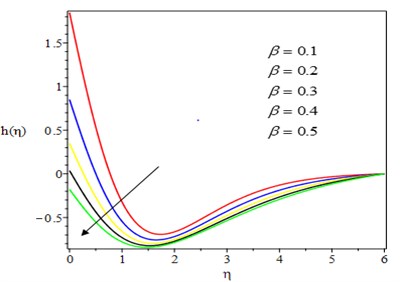
Fig. 9Effect of Chemical reaction parameter on the concentration profile

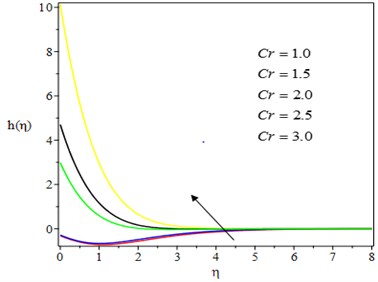
Fig. 10Effect of unsteadiness parameter on temperature profile

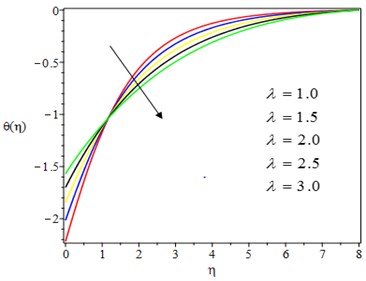
Table 1Skin friction coefficients, Nusselt number and Sherwood number of various values of important parameters where, A*=B*=Ec=γ=0.1, K1=R=0.5, Bic=Bit=1.0

$β$	M	Cr	$λ$	Cfx	Cfy	Nu	Sh
0.1	0.5	0.1	0.5	–5.106011	31.858097	0.519260	–1.661414
0.2				–3.831593	13.220039	0.685547	–0.8490386
0.3				–3.292098	7.590677	0.794603	–0.383889
0.4				–2.982865	4.964475	0.874366	–0.067096
0.5				–2.780840	3.436612	0.936103	0.181934
0.5	0.0	0.1	0.5	–2.557637	4.182315	0.815603	–0.022393
	0.5			–2.780840	3.436612	0.936104	0.181934
	1.0			–2.997403	2.850816	1.040385	0.335933
	1.5			–3.155939	2.367540	1.132998	0.459937
	2.0			–3.320810	1.955465	1.216798	0.564124
0.5	0.5	0.0	0.5	–2.766751	3.265498	0.936166	0.023647
		0.3		–2.816733	3.781496	0.935751	0.525625
		0.5		–2.865144	4.176897	0.935104	0.930996
		1.0		–3.076173	5.835048	0.931645	2.405443
		1.5		–1.084563	0.460314	0.962170	–16.102385
0.5	0.5	0.1	1.0	–2.929721	3.654077	0.191477	–0.342295
			1.5	–3.113362	3.046629	1.023925	–0.172345
			2.0	–3.282556	2.539055	1.119785	–0.031366
			2.5	–3.445025	2.099725	1.205966	0.089965
			3.0	–3.587719	1.371037	1.285665	0.196654

5. Conclusions

Transient analysis of a three-dimensional, heat and mass transfer, viscous incompressible, laminar, MHD boundary layer flow analysis of a Casson – nanofluid over a stretching sheet in porous media was considered. The system of highly nonlinear partial differential equations is reduced to a system of ordinary differential equations through appropriate existing similarity transformation. The resulting equations are solved through Garlekin finite element method. The results obtained through FEM are verified by other numerical solutions via Runge– Kutta fourth - order integration scheme.

The following are the findings from the study:

1) The momentum boundary layer reduces as the Casson parameter increases and the velocity profile is enhanced.

2) The unsteadiness parameter can be used to adjust the thickness of the momentum boundary layer and as well as the thermal boundary layer.

3) The concentration profiles are highly influenced and are decelerated with higher value of chemical reaction parameter.

4) The Nusselt number depreciated, and Sherwood number increases with the higher values of chemical reaction parameter.

4) The heat transfer rate can be enhanced by varying the value of the magnetic field.

5) Increase in the unsteadiness parameter also increases the skin friction coefficients, heat transfer rate, and as well as the mass transfer rate.

References

H. R. Patel, “Effects of cross diffusion and heat generation on mixed convective MHD flow of Casson fluid through porous medium with non-linear thermal radiation,” Heliyon, Vol. 5, No. 4, p. e01555, Apr. 2019, https://doi.org/10.1016/j.heliyon.2019.e01555

Publisher
M. Sobamowo, “Finite element analysis of flow and heat transfer of dissipative Casson-Carreau nanofluid over a stretching sheet embedded in a porous medium,” Aeronautics and Aerospace Open Access Journal, Vol. 2, No. 5, Oct. 2018, https://doi.org/10.15406/aaoaj.2018.02.00064

Publisher
S. Shehzad, T. Hayat, and A. Alsaedi, “Three-dimensional MHD flow of Casson fluid in porous medium with heat generation,” Journal of Applied Fluid Mechanics, Vol. 9, No. 1, pp. 215–223, Jan. 2016, https://doi.org/10.18869/acadpub.jafm.68.224.24042

Publisher
S. Nadeem, R. U. Haq, N. S. Akbar, and Z. H. Khan, “MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet,” Alexandria Engineering Journal, Vol. 52, No. 4, pp. 577–582, Dec. 2013, https://doi.org/10.1016/j.aej.2013.08.005

Publisher
I. Ullah, K. Bhattacharyya, S. Shafie, and I. Khan, “Unsteady MHD mixed convection slip flow of casson fluid over nonlinearly stretching sheet embedded in a porous medium with chemical reaction, thermal radiation, heat generation/absorption and convective boundary conditions,” PLOS ONE, Vol. 11, No. 10, p. e0165348, Oct. 2016, https://doi.org/10.1371/journal.pone.0165348

Publisher
N. Freidoonimehr and A. B. Rahimi, “Brownian motion effect on heat transfer of a three-dimensional nanofluid flow over a stretched sheet with velocity slip,” Journal of Thermal Analysis and Calorimetry, Vol. 135, No. 1, pp. 207–222, Jan. 2019, https://doi.org/10.1007/s10973-018-7060-y

Publisher
S. Shateyi, “Numerical analysis of three‐dimensional MHD nanofluid flow over a stretching sheet with convective boundary conditions through a porous medium,” Nanofluid Heat and Mass Transfer in Engineering Problems, Mar. 2017, https://doi.org/10.5772/65803

Publisher
Q. M. Zaigham Zia, I. Ullah, M. Waqas, A. Alsaedi, and T. Hayat, “Cross diffusion and exponential space dependent heat source impacts in radiated three-dimensional (3D) flow of Casson fluid by heated surface,” Results in Physics, Vol. 8, pp. 1275–1282, Mar. 2018, https://doi.org/10.1016/j.rinp.2018.01.001

Publisher
G. Mahanta and S. Shaw, “3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition,” Alexandria Engineering Journal, Vol. 54, No. 3, pp. 653–659, Sep. 2015, https://doi.org/10.1016/j.aej.2015.04.014

Publisher
R. Kandasamy and P. G. Palanimani, “Effects of chemical reactions, heat, and mass transfer on nonlinear magnetohydrodynamic boundary layer flow over a wedge with a porous medium in the presence of ohmic heating and viscous dissipation,” Journal of Porous Media, Vol. 10, No. 5, pp. 489–502, 2007, https://doi.org/10.1615/jpormedia.v10.i5.60

Publisher
I. Ullah, I. Khan, and S. Shafie, “MHD natural convection flow of Casson nanofluid over nonlinearly stretching sheet through porous medium with chemical reaction and thermal radiation,” Nanoscale Research Letters, Vol. 11, No. 1, pp. 1–15, Dec. 2016, https://doi.org/10.1186/s11671-016-1745-6

Publisher
G. T. Thammanna, K. Ganesh Kumar, B. J. Gireesha, G. K. Ramesh, and B. C. Prasannakumara, “Three dimensional MHD flow of couple stress Casson fluid past an unsteady stretching surface with chemical reaction,” Results in Physics, Vol. 7, pp. 4104–4110, 2017, https://doi.org/10.1016/j.rinp.2017.10.016

Publisher
M. Monica, J. Sucharitha, and C. H. Kishore, “Effects of exothermic chemical reaction with Arrhenius activation energy, non – uniform heat source/sink on MHD stagnation point flow of a Casson fluid over a nonlinear stretching sheet with variable fluid properties and slip conditions,” Journal of the Nigerian Mathematical Society, Vol. 36, pp. 163–190, 2017.

Search CrossRef
A. Jasmine Benazir, R. Sivaraj, and O. D. Makinde, “Unsteady magnetohydrodynamic Casson fluid flow over a vertical cone and flat plate with non-uniform heat source/sink,” International Journal of Engineering Research in Africa, Vol. 21, pp. 69–83, Dec. 2015, https://doi.org/10.4028/www.scientific.net/jera.21.69

Publisher
A. Khalid, I. Khan, A. Khan, and S. Shafie, “Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium,” Engineering Science and Technology, an International Journal, Vol. 18, No. 3, pp. 309–317, Sep. 2015, https://doi.org/10.1016/j.jestch.2014.12.006

Publisher
E. O. Fatunmbi and O. J. Fenuga, “MHD Micropolar fluid over a permeable stretching sheet in the presence of variable viscosity and thermal conductivity with Soret and Dufour effects,” International Journal of Mathematical Analysis and Optimization: Theory and Applications, pp. 211–232, 2017.

Search CrossRef
K. Kalyani, K. Sreelakshmi, and G. Sarojamma, “The three – dimensional flow of a non – Newtonian fluid over a flat surface through a porous medium with surface convective conditions,” Global Journal of Pure and Applied Mathematics, Vol. 13, pp. 2193–2211, 2017.

Search CrossRef
P. Renuka, B. Ganga, K. Kalivanan, and A. K. Abdul Hakeem, “Slip effects on ohmic dissipative non-Newtonian fluid flow in the presence of aligned magnetic field,” Journal of Applied and Computational Mechanics, Vol. 6, No. 2, pp. 296–306, Apr. 2020, https://doi.org/10.22055/jacm.2019.29024.1543

Publisher
A. K. Pandey and M. Kumar, “Effect of viscous dissipation and suction/injection on MHD nanofluid flow over a wedge with porous medium and slip,” Alexandria Engineering Journal, Vol. 55, No. 4, pp. 3115–3123, Dec. 2016, https://doi.org/10.1016/j.aej.2016.08.018

Publisher
A. S. Odesola, I. O. Abiala, F. O. Akinpelu, and O. J. Fenuga, “Analysis of magnetohydrodynamic (MHD) nanofluid flow with heat and mass transfer over a porous stretching sheet,” International Journal of Applied Mechanics and Engineering, Vol. 25, No. 4, pp. 162–174, Dec. 2020, https://doi.org/10.2478/ijame-2020-0056

Publisher
A. S. Odesola, I. O. Abiala, and O. J. Fenuga, “Effect of Brownian motion and thermophoresis on heat and mass transfer of a three – dimensional Casson fluid flow over a stretching sheet with velocity slip,” International Nigerian Journal of Mathematics Application, Vol. 31, pp. 77–96, 2021.

Search CrossRef
B. J. Gireesha and N. G. Rudraswamy, “Chemical reaction on MHD flow and heat transfer of a nanofluid near the stagnation point over a permeable stretching surface with non-uniform heat source/sink,” International Journal of Engineering, Science and Technology, Vol. 6, No. 5, pp. 13–25, Jan. 1970, https://doi.org/10.4314/ijest.v6i5.2

Publisher
C. Sulochana, S. S. Payad, and N. Sandeep, “Non-uniform heat source or sink effect on the flow of 3D Casson fluid in the presence of soret and thermal radiation,” in International Journal of Engineering Research in Africa, Vol. 20, pp. 112–129, Oct. 2015, https://doi.org/10.4028/www.scientific.net/jera.20.112

Publisher
L. Kumar, “Finite element analysis of combined heat and mass transfer in hydromagnetic micropolar flow along a stretching sheet,” Computational Materials Science, Vol. 46, No. 4, pp. 841–848, Oct. 2009, https://doi.org/10.1016/j.commatsci.2009.04.021

Publisher
I. O. Abiala and J. A. Gbadeyan, “Finite element dynamic analysis of non-uniform beams on variable one-parameter foundation subjected to uniformly distributed moving loads,” International Journal of Applied Mechanics and Engineering, Vol. 20, No. 4, pp. 693–715, Dec. 2015, https://doi.org/10.1515/ijame-2015-0046

Publisher
G. Swapna, L. Kumar, P. Rana, A. Kumari, and B. Singh, “Finite element study of radiative double-diffusive mixed convection magneto-micropolar flow in a porous medium with chemical reaction and convective condition,” Alexandria Engineering Journal, Vol. 57, No. 1, pp. 107–120, Mar. 2018, https://doi.org/10.1016/j.aej.2016.12.001

Publisher
P. S. Reddy, P. Sreedevi, and A. J. Chamkha, “MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction,” Powder Technology, Vol. 307, pp. 46–55, Feb. 2017, https://doi.org/10.1016/j.powtec.2016.11.017

Publisher

About this article

Received

14 July 2022

Accepted

22 September 2022

Published

18 October 2022

DOI

https://doi.org/10.21595/jets.2022.22815

Keywords

Casson nanofluid

chemical reaction

finite element method

MHD

porous stretching sheet

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 02 21

Multi-factor coupled thermal simulation of flat-panel digital PCR structure

Qixuan Li, Xulei Qin, Haoyu Wang

Research article

2023 12 30

Joint effects of thermal diffusion and diffusion thermo on MHD three dimensional nanofluid flow towards a stretching sheet

G. Murali, G. Deepa, Nirmala Kasturi V, T. Poornakantha

Research article

2023 11 17

Thermal performance investigation of porous fins with convection and radiation under the influence of magnetic field using optimal homotopy asymptotic method

M. G. Sobamowo, H. Berrehal, A. B. Ajayi, O. K. Onanuga, R. O. Fawumi

Research article

2019 05 15

Effect of heat transfer optimization on brake noise characteristics of automotive disc brake

Sen Zhang, Jian Zhang

A. S. Odesola, I. O. Abiala, M. G. Sobamowo, and O. J. Fenuga, “Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction,” Journal of Engineering and Thermal Sciences, Vol. 2, No. 2, pp. 100–113, Oct. 2022, https://doi.org/10.21595/jets.2022.22815

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2022.22815
UR  - https://doi.org/10.21595/jets.2022.22815
TI  - Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction
T2  - Journal of Engineering and Thermal Sciences
AU  - Odesola, A. S.
AU  - Abiala, I. O.
AU  - Sobamowo, M. G.
AU  - Fenuga, O. J.
PY  - 2022
DA  - 2022/10/18
PB  - JVE International Ltd.
SP  - 100-113
VL  - 2
IS  - 2
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Odesola_2022,
	doi = {10.21595/jets.2022.22815},
	url = {https://doi.org/10.21595/jets.2022.22815},
	year = 2022,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {2},
	number = {2},
	pages = {100--113},
	author = {A. S. Odesola and I. O. Abiala and M. G. Sobamowo and O. J. Fenuga},
	title = {Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]A. S. Odesola, I. O. Abiala, M. G. Sobamowo, and O. J. Fenuga, “Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction,” Journal of Engineering and Thermal Sciences, vol. 2, no. 2, pp. 100–113, Oct. 2022, doi: 10.21595/jets.2022.22815.

Copy IEEE

Copied to clipboard!

Odesola, A. S., I. O. Abiala, M. G. Sobamowo, and O. J. Fenuga. “Transient Three-Dimensional Magnetohydrodynamic Flow of Heat and Mass Transfer of a Casson Nanofluid Past a Stretching Sheet with Non-Uniform Heat Source/Sink, Thermal Radiation and Chemical Reaction.” Journal of Engineering and Thermal Sciences 2, no. 2 (October 18, 2022): 100–113. https://doi.org/10.21595/jets.2022.22815.

Copy Chicago

Copied to clipboard!

Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction

Abstract

Highlights

1. Introduction

2. Mathematical model of the problem

3. Method of solution

4. Results and discussion

5. Conclusions

References

About this article

Related Articles