Abstract
This communication reports the joint effects of Thermal Diffusion and Diffusion Thermo on viscous and incompressible three-dimensional nanofluid flow towards a stretching sheet in connection to the influence of a magnetic field. In this study, nanofluid model is employed for the effects of thermophoresis and Brownian motion. Following that, similarity variables are chosen to turn the dimensional nonlinear system into dimensionless expressions and the resultant transformed equations are solved numerically using Finite Element method. Special emphasis has been given to the parameters of physical interest. These findings are visually presented through graphical representations, providing a clear and insightful understanding involved in this flow scenario. In addition, the final results are examined in light of past research and it is determined that they meet the convergence standards to an exceedingly satisfactory degree. The study’s findings are beneficial for many technical and commercial endeavours.
Highlights
- Extensive numerical parametric study is performed on the numerical explanation of a class of nonlinear equations to describe the details of the solution and delivers a comprehensive analysis of how various factors, including the nanofluid properties and other pertinent parameters, influence the flow variables.
- The study's findings are beneficial for many technical and commercial endeavors.
- The finite element method employed in the current study can be used in future research since it is a highly useful approach to solving linear and nonlinear partial and ordinary differential equations in physics, mechanical engineering, and other related subjects.
- The resulting findings are more accurate than those obtained using other numerical approaches.
- The current study is considered to examine heat and mass transfer effects across a vertically stretched surface under the light of double diffusion effects due to importance in practical, industrial, and technical consequences.
- Increasing values of Magnetic field parameter, the fluid velocities along x and y - directions are decreasing due to Lorentz force.
1. Introduction
In-depth research has been started to examine the thermophysical characteristics of typical heat transfer fluids. However, the escalating demands of contemporary technologies cannot be met by these fluids. Thus, the addition of nanoparticles to such fluids is started in order to overcome these obstacles. Engineered nanofluids are made up of a base fluid and nanoparticles. The base fluid is used to produce these liquids by incorporating nano-sized particles into it. Recent research have demonstrated through experimentation that the inclusion of nanoparticles increases the thermal conductivity of conventional fluids significantly. A connection between micro and macro molecular structures has been established thanks to the new inherent properties of nanofluids. Nanofluids are extremely important in many heat transfer processes such as fuel cells, microelectronics, hybrid-powered engines, and so on because of their remarkable qualities. Because of its utility in the creation of high-quality lubricants and oils, nanofluids are utilized in industrial technologies. Fluid mass and heat transfer vary as a consequence of the difference in density between fluid flux and fluid flow regime. The interaction between composition gradients (Dufour) and temperature gradients is one of two possible processes that might lead to the generation of thermal diffusion (Soret). Although their advantages in hydrology, petrology, geosciences, isotope separation, and other fields have been shown [1], their influence on the fluid density differential in fluid flow regimes is still significant. Kaladhar et al. [2] investigated the impact of Soret and Dufour on chemically reacting mixed convection flow in an annulus with Navier slip and convective boundary conditions. The effects of thermophoresis, Soret, and Dufour on the heat and mass transfer flow of a magnetohydrodynamics non-Newtonian nanofluid over an inclined plate were examined by Idowu and Falodun [3]. In order to investigate the combined effects of Soret, Dufour, and radiation of a viscoelastic fluid over an exponentially growing surface, Kasali et al. [4] employed the Cattaneo-Christov heat flux model. In an inclined rectangular enclosure with a partly saturated porous wall, Hu and Mei [5] studied the combined effects of heat and moisture convection and entropy production in the presence of Soret and Dufour numbers. The combined effects of Dufour and Soret on three-dimensional compressed flow and heat transfer in a spinning tube were examined by Yinusa et al. [6]. The effect of Soret and Dufour on thermo-solute convection was examined by Rghif et al. [7]. In double diffusive mixed convection, Hussain et al. [8] examined the effect of Dufour and Soret on the power law fluid and magnetic field parameters. Using the finite difference approach, Khan et al. [9] examined the Darcy-Forchheimer flow of a viscous fluid with Dufour and Soret effects. Numerical solutions for the MHD flow with Soret and Dufour effects were created by Hayat et al. [10]. The Soret and Dufour effects were taken into consideration when Hayat et al. [11] investigated the influence of chemical processes on the peristaltic motion of an MHD-coupled fluid in a channel. The effects of Soret-Dufour, heat radiation, and binary chemical reaction on the Darcy-Forchheimer flow of nanofluids were studied by Rasool et al. [12]. In a Hall MHD generator system, Usman et al study's team [13] looked into the impacts of Soret, Dufour, and activation energy on the double diffusive convective pair stress micropolar nanofluid flow. The effects of chemical reaction, thermo-diffusion, and diffusion-thermo on the MHD flow of an incompressible nanofluid over a uniformly elongating sheet were examined by Reddy and Chamkha [14]. In a container holding liquid metal, Arun and Satheesh [15] explain MHD double diffusive natural convection and entropy generation. The slip effects of MHD unsteady Maxwell nanofluid flow across a permeable stretched sheet with radiation and thermo-diffusion in the presence of a chemical reaction were examined by Ali et al. [16] using the finite element method. The combined effects of thermo-diffusion and heat radiation on a porous sheet that could contract and stretch while carrying a Williamson nanofluid were investigated by Bhatti and Rashidi [17]. In a porous cage containing nanofluid, Aly [18] investigated thermo-diffusion-influenced spontaneous convection across circular cylinders. M. C. Krishna Reddy et al. [19]studied Heat and mass transfer effects on unsteady MHD free convection flow past a vertical permeable moving plate with radiation. S. Sivaiah et al. [20] Found the solution for Unsteady MHD mixed convection flow past a vertical porous plate in prsesence of radiation. M. Gundagani et al. [21] analysed the Radiation Effects on an Unsteady MHD Convective Flow Past a Semi-Infinite Vertical Permeable Moving Plate Embedded in a Porous Medium with Viscous Dissipation. Deepa Gadipally et al. [22] Studied on Analysis of soret and dufour effects on unsteady MHD flow past a semi infinite vertical porous plate via finite difference method. G. Deepa et al. [23] Studied the Effects of viscous dissipation on unsteady MHD free convective flow with thermophoresis past a radiate inclined permeable plate. Murali G. et al. [24] applied FEM on numerical study of chemical reaction effects on unsteady MHD fluid flow past an infinite vertical plate embedded in a porous medium with variable suction. For better understanding of the concept and its applications are covered by references [25-30].
It is crucial to evaluate thermal diffusion and thermal diffusion effects on steady, incompressible, viscous, electrically conducting, three-dimensional, MHD-Nanofluid flow over a stretched sheet in the presence of magnetic field, Brownian motion, and thermophoresis effects. The intellectual curiosity and technical applications of non-Newtonian rheology have greatly piqued academics’ attention. Because of its generous and prized application in industrial production mechanisms, power engineering, petroleum production, and a wide range of chemical processes, non-Newtonian fluids have been the subject of several studies in recent years. A single constitutive relation is insufficient to fully describe the features of all non-Newtonian fluids, hence they are classified categorically into several models. Visco-inelastic fluids, visco-elastic fluids, polar fluids, anisotropic fluids, and fluids with microstructure are the main classifications of these models. Visco-inelastic fluids, which integrate the combined effects of elastic and viscous characteristics, are among them and represent the most important subclass of non-Newtonian fluid.
This review is motivated by the aforementioned sources as well as the different potential industrial applications of the topic. The current study is considered to examine heat and mass transfer effects across a vertically stretched surface under the light of double diffusion effects due to importance in practical, industrial, and technical consequences. From the literature review mentioned above, it can be concluded that this issue has never been addressed. First, by using compatible transformations, the challenging partial equations are transformed into useful ordinary differential equations for this purpose. To develop numerical solutions with increased computing efficiency, the finite element method is utilised.
The goal of this research is to elaborate on the findings of Khan et al. [25]. Along with the effects of skin friction, the rate of heat transfer and mass transfer coefficients on fluid flow, relevant variables including velocity, temperature, and concentration profiles are given.
2. Mathematical formulation
When thermophoresis, Brownian motion, and the effects of magnetic fields are present, the combined effects of Soret and Dufour on the flow of a nanofluid that is viscous, electrically conducting, incompressible, and three-dimensional are investigated. The nanofluid in question possesses all of these characteristics. The nanofluid under consideration is one that moves in a three-dimensional manner across a sheet that has been stretched. Investigations are now being carried out to learn more about how nanofluids behave while moving over a stretched sheet. As a result of the findings of this investigation, we are in a position to hypothesise the following things:
1) For the stretching sheet, the variable thickness is assumed as .
2) Also, the stretched velocity of the sheet is and this is suitable for since demotes the flat stretching sheet.
The magnetic Reynolds number has to be as low as it is physically possible to make it in order to dismiss the magnetic field that is formed. This is the case in order to disregard the magnetic field that is created.
In this work, the authors have preferred Magnetic field of strength is applied to the flow.
The following are the equations that should be used for flow control in line with the ideas that have been discussed up to this point:
Continuity equation:
Momentum equations:
Equation of thermal energy:
Equation of species concentration:
The boundary conditions for this flow are:
where:
If you use the following similarity transformations and convert the governing equations to ordinary differential equations, you should be able to get the answers that you are seeking for:
The continuity equation, which is validated by Eq. (9), is provided in the following form, which is also used by Eqs. (2), (3), (4), and (5):
As a direct consequence of this Eq. (6), the following boundary constraints are imposed on the system:
When referring to the subject matter at hand, many of the components that go into making it up are referred to as:
The Sherwood number, the skin-friction coefficient, and the local Nusselt number are:
where and are local Reynolds numbers.
3. Method of solution
Numerical modelling and simulation provide an easier, cheaper and highly efficient way to find solutions to complex mathematical equations. The development of computer numerical modelling has been useful in simplifying the problem-solving procedure. Numerical models are developed to perfectly match the physical system, and the solutions can be analyzed and checked against the real system. These numerical methods allow us to improve approaches to the physical system and solve it quickly. The finite element method employed in the current study can be used in future research since it is a highly useful approach to solving linear and nonlinear partial and ordinary differential equations in physics, mechanical engineering, and other related subjects. The following are the advantages of FEM technique:
– Modelling
– Adaptability
– Accuracy
– Boundaries
– Visualization
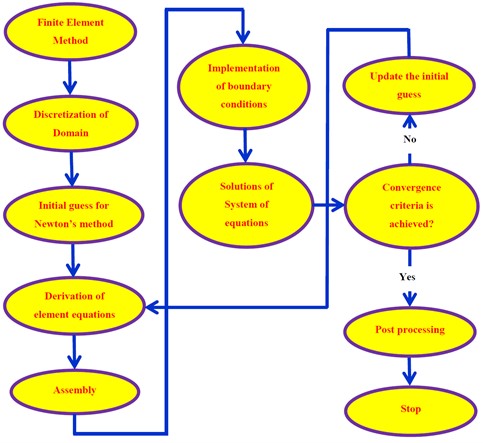
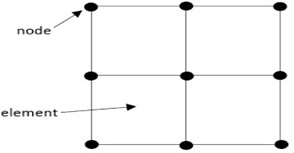
The use of the finite element approach is shown in Fig. 1, which also serves as an example. The resolution of generated equations may be accomplished by the use of a wide variety of numerical techniques, including the LU decomposition method, the Gauss elimination method, and a great deal more besides. The solution of built equations is one of the most popular uses for these approaches. When working with real numbers, it is very necessary to bear in mind the form functions that are used to make an approximate approximation of real functions. Form functions may be used to provide a close approximation of real functions. If you follow this technique step by step, you may be certain that your calculations will be accurate. The flow domain has a total of 20,001 nodes and is divided into 10,000 quadratic components that are all the same size.
These components are all of the same shape. The flow domain is made up of 10,000 quadratic components, all of which are of the same magnitude as their counterparts in the other components. After the element equations were developed, there were a total of 80,004 nonlinear equations that could be investigated. These equations were made accessible for study. After the boundary conditions have been applied, the Gauss approach is used to remove the remaining system of nonlinear equations, and then the Gauss technique is used to arrive at a numerical solution that is accurate to 0.00001 degrees. The use of gaussian quadrature is done so that the challenges that are connected to integration may be aided in some way.
Fig. 1Finite element method flow chart and meshing diagram
Program code validation.
Table 1Comparison of present finite element method results with published results of Khan et al. [25] for Sr=Du=M=Le= 0
Pr | Present Nusselt number results | Nusselt number results of Khan et al. [25] |
7.0 | 2.39698362139067130947561 | 2.404797 |
13.0 | 2.69678670983769138713347 | 2.705551 |
25.0 | 3.27565748503561087643423 | 3.287794 |
50.0 | 4.10875617938673896398386 | 4.115197 |
100.0 | 5.32767687587319873698139 | 5.336685 |
Table 1 compares the most recent finite element Nusselt number (rate of heat transfer) results with those that Khan et al. [25] had previously reported using the shooting method with the fourth- to fifth-order Runge-Kutta integration method without taking into account the effects of thermal diffusion, diffusion thermo, magnetic field, and Lewis number. As this table demonstrates, there is a strong correlation between the new findings and the outcomes that Khan et al. [25] previously established.
4. Results and discussion
In this results and discussion section, the authors have to study the effects of the different physical parameters namely Magnetic field parameter (), Prandtl number (), Thermophoresis parameter (), Brownian motion parameter (), Lewis number (), Diffusion thermo parameter (), Thermal diffusion parameter (Sr) and Velocity power index parameter () are presented through Fig. 3 to 16 for dimensionless velocity, temperature and concentration () profiles. Also, the effects of same parameters are discussed on engineering quantities namely Skin-friction coefficient, Nusselt number (rate of heat transfer coefficient), Sherwood number (rate of mass transfer coefficient) are discussed with help of numerical values in tabular forms.
Effect of Magnetic field parameter (): Figs. 2 and 3 intend the velocity profiles and for various values of (Magnetic field parameter). It is observed that velocity fields and decline when the values of increases. The application of an applied magnetic field has the tendency to slow down the movement of the fluid, which leads to a decrease in the velocity and momentum boundary layer thickness. The influence of Magnetic field parameter () on Skin-friction coefficient is discussed in Table 2. From this table, it is observed that, the Skin-friction coefficient is decreasing with increasing values of Magnetic field parameter.
Fig. 2f'η profiles for deviations of M
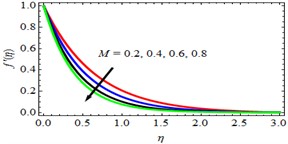
Fig. 3g'η profiles for deviations of M
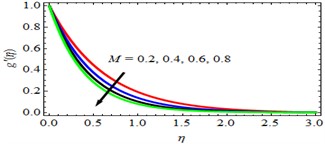
Table 2Skin-friction coefficient Cfx values for different values of M, Pr, Nt, Nb, n, Sr, Du and Le
0.2 | 0.71 | 0.1 | 0.1 | 0.1 | 0.5 | 0.5 | 0.3 | 2.376518457634875 |
0.4 | 2.346574687580164 | |||||||
0.6 | 2.326786768709389 | |||||||
1.00 | 2.330867069736953 | |||||||
3.00 | 2.310560986703987 | |||||||
0.3 | 2.404758471653743 | |||||||
0.5 | 2.423034839876236 | |||||||
0.3 | 2.392328956490934 | |||||||
0.5 | 2.414467037460111 | |||||||
0.2 | 2.406787110387667 | |||||||
0.3 | 2.426470107340303 | |||||||
0.8 | 2.397778556767339 | |||||||
1.0 | 2.415656787287387 | |||||||
1.0 | 2.402564107354705 | |||||||
1.5 | 2.426676872736475 | |||||||
0.7 | 2.347785290756908 | |||||||
0.9 | 2.313567577575207 |
Effect of Velocity power index parameter (): The influence of (Velocity power index parameter) on velocity profiles ( and ), temperature () and concentration () profiles are discussed in Figs. 4-7. From these figures, it is observed that the velocity profiles ( and ), temperature () and concentration () profiles are increasing with increasing values of n (Velocity power index parameter). The effect of Velocity power index parameter () on Skin-friction coefficient, Rate of heat transfer and mass transfer coefficients are discussed in Tables 2, 3 and 4 respectively. From these tables, it is observed that, the Skin-friction, Rate of heat transfer and mass transfer coefficients are increasing with increasing values of Velocity power index parameter.
Effect of Prandtl number (): Fig. 8 illustrates the link that exists between the Prandtl number and the temperature of the fluid whose temperature is being measured. As the value of continues to increase, the temperature gradient of the fluid will give off the impression of being less striking. When increases, so does the momentum diffusivity, which eventually overtakes the thermal diffusivity and becomes the dominant one. This happens when momentum diffusivity finally overtakes thermal diffusivity. There is a good chance that the amount of heat that can be transferred by a fluid is in some way related to the speed at which the fluid is moving. This has the immediate effect of reducing the thickness of the boundary layer, which in turn results in an increase in the rate at which heat is carried. The effect that the Prandtl number, which is more commonly referred to as , has on the rate of heat transfer coefficient is broken down and discussed in Table 3. According to the data presented in the table, the rate of the heat transfer coefficient tends to decrease as the Prandtl number rises. This is indicated by the downward trend seen in this rate.
Fig. 4f'η profiles for deviations of n
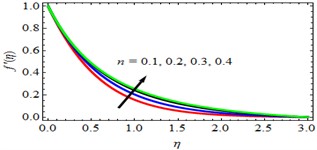
Fig. 5g'η profiles for deviations of n
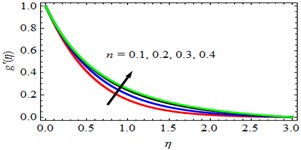
Fig. 6θη profiles for deviations of n
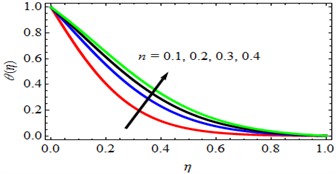
Fig. 7ϕη profiles for deviations of n
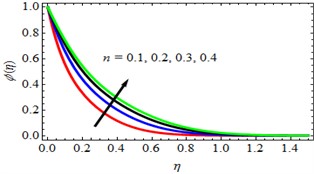
Table 3Skin-friction coefficient Cfy values for different values of M, Pr, Nt, Nb, n, Sr, Du and Le
0.2 | 0.71 | 0.1 | 0.1 | 0.1 | 0.5 | 0.5 | 0.3 | 1.267896398713986 |
0.4 | 1.228678209386932 | |||||||
0.6 | 1.209678676901767 | |||||||
1.00 | 1.218081896618944 | |||||||
3.00 | 1.197098285694984 | |||||||
0.3 | 1.280897892741818 | |||||||
0.5 | 1.316786529873929 | |||||||
0.3 | 1.285413403369393 | |||||||
0.5 | 1.309376036137032 | |||||||
0.2 | 1.299687200698301 | |||||||
0.3 | 1.320986729849287 | |||||||
0.8 | 1.296713670933986 | |||||||
1.0 | 1.327643109334933 | |||||||
1.0 | 1.309857666686248 | |||||||
1.5 | 1.336790868733696 | |||||||
0.7 | 1.245745637901711 | |||||||
0.9 | 1.229954901934930 |
Effect of Brownian motion parameter (): Using the data that is shown in Figs. 9 and 10, the authors came to the conclusion that an increase in the Nb, which is the parameter that describes the Brownian motion, results in a drop in the concentration fields and a rise in temperature. The thermophoresis and Brownian motion coefficients of individual nanoparticles do not all have the same values. This is a well-established scientific fact. This exemplifies the fact that New Brunswick possesses breathtakingly gorgeous natural scenery. Tables 2, 3, and 4 respectively analyse the effect that the Brownian motion parameter has on the skin friction, the rate of heat transfer, and the mass transfer coefficients. If you take a look at these tables, you'll see that the value of the Brownian motion parameter causes the skin-friction and rate of heat transfer coefficients to increase, whilst the rate of mass transfer coefficient decreases. This is something that you can observe for yourself. In the case of the rate of mass transfer coefficient, one observes the impact that is directly opposite.
Fig. 8θη profiles for deviations of Pr
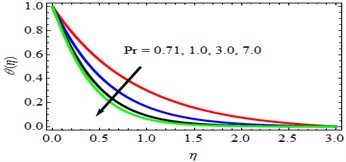
Fig. 9θη profiles for deviations of Nb
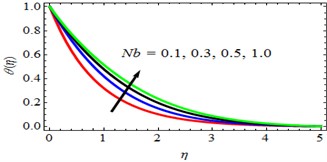
Fig. 10ϕη for deviations of Nb
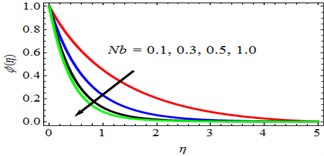
Fig. 11θη profiles for deviations of Nt
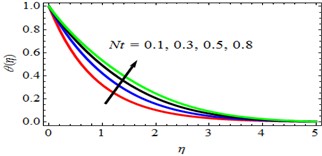
Fig. 12ϕη for deviations of Nt
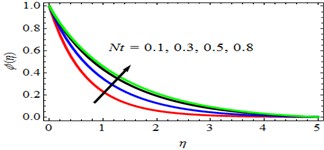
Fig. 13ϕη for deviations of Le
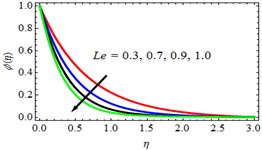
Fig. 14θη profiles for deviations of Du
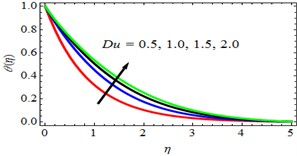
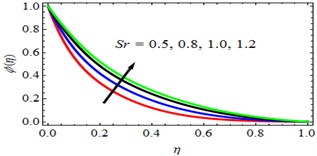
Fig. 15ϕη for deviations of Sr
Effect of Dufour number or Diffusion thermo parameter (): Fig. 14 showed that the fluid temperature profile rose along with the rise in the Dufour number. This phenomenon may be explained physically as what would happen if two separate fluids with the same temperature and no chemical reaction were discharged into the system and allowed to spread. The temperature differential in the system would increase. Tables 2 and 3 explore, respectively, how the Dufour number affects skin friction and the rate of heat transfer coefficients. These data show that when the Dufour number rises, both skin friction and the rate of heat transfer coefficients increase.
Effect of Soret number or Thermal diffusion parameter (): The influence of the Soret number on concentration profiles and the subsequent increase in fluid concentration is seen in Fig. 15. The Soret effect takes place when an irreversible process results in a temperature gradient in a concentration field. This causes the field to have a gradient. It is likely to result in an increase in the concentration flux of the flow system. Fig. 15 gives an explanation. The effect that the Soret number has on the rate of mass transfer coefficients and the skin friction is investigated in Tables 2 and 4, respectively. According to these data, a rise in the Soret number results in an increase in the rate of mass transfer coefficients as well as an increase in the skin friction.
Table 4Rate of heat transfer coefficient Nux values for different values of Pr, Nb, Nt, n and Du
0.71 | 0.1 | 0.1 | 0.1 | 0.5 | 0.746187561347563 |
1.00 | 0.707856729847486 | ||||
3.00 | 0.670804287489651 | ||||
0.3 | 0.769782183756867 | ||||
0.5 | 0.780298476173734 | ||||
0.3 | 0.779717360931973 | ||||
0.5 | 0.793736631397399 | ||||
0.2 | 0.772556776400390 | ||||
0.3 | 0.797670987097368 | ||||
1.0 | 0.786768609816987 | ||||
1.5 | 0.812598919086301 |
Table 5Rate of mass transfer coefficient Shx values for different values of Le, Nb and Nt
0.3 | 0.5 | 0.1 | 0.1 | 0.5 | 0.895678168053718 |
0.7 | 0.853665034039290 | ||||
0.9 | 0.821067039160937 | ||||
0.5 | 0.866786908742823 | ||||
0.8 | 0.849871987659872 | ||||
0.3 | 0.919610369829839 | ||||
0.5 | 0.930896981367903 | ||||
0.2 | 0.903565706418738 | ||||
0.3 | 0.922060361073783 | ||||
0.8 | 0.916673187346049 | ||||
1.0 | 0.931604176304393 |
5. Conclusions
In this current research work, Finite element method is implemented to provide the numerical solutions of nanofluid parameters in three dimensional flows. The numerical solutions are used to study the three dimensional structures with the flow of nanofluid to investigate the influence of well-known fluid parameters and the final results are:
1) Increasing values of Magnetic field parameter, the fluid velocities along and – directions are decreasing due to Lorentz force.
2) Rising values of Velocity power index parameter, the fluid velocities along and – directions are growing.
3) Increasing values of Prandtl number decreases temperature profiles and the reverse effect is noticed in case of rising values of Dufour number, Velocity power index parameter, Thermophoresis parameter and Brownian motion parameters.
4) In case of increasing values of Thermophoresis parameter, Soret number, Velocity power index parameter, the Concentration profiles are decreases and reduce for in case of Brownian motion parameter and Lewis number.
5) Finally, for program code validation, the authors have compared the present research work with the published results of Khan et al. [25] and observed good agreement.
References
-
M. T. Akolade, A. S. Idowu, and A. T. Adeosun, “Multislip and Soret-Dufour influence on nonlinear convection flow of MHD dissipative Casson fluid over a slendering stretching sheet with generalized heat flux phenomenon,” Heat Transfer, Vol. 50, No. 4, pp. 3913–3933, Jun. 2021, https://doi.org/10.1002/htj.22057
-
K. Kaladhar, E. Komuraiah, and K. M. Reddy, “Soret and Dufour effects on chemically reacting mixed convection flow in an annulus with Navier slip and convective boundary conditions,” Applied Mathematics and Nonlinear Sciences, Vol. 4, No. 2, pp. 475–488, Dec. 2019, https://doi.org/10.2478/amns.2019.2.00045
-
A. S. Idowu and B. O. Falodun, “Effects of thermophoresis, Soret-Dufour on heat and mass transfer flow of magnetohydrodynamics non-Newtonian nanofluid over an inclined plate,” Arab Journal of Basic and Applied Sciences, Vol. 27, No. 1, pp. 149–165, Jan. 2020, https://doi.org/10.1080/25765299.2020.1746017
-
K. B. Kasali, Y. O. Tijani, M. O. Lawal, and Y. T. Lawal, “Soret, Dufour and radiation effects of a viscoelastic fluid on an exponentially stretching surface using the Catteneo-Christov heat flux model,” Multidiscipline Modeling in Materials and Structures, Vol. 16, No. 6, pp. 1577–1594, Jun. 2020, https://doi.org/10.1108/mmms-11-2019-0202
-
J.-T. Hu and S.-J. Mei, “Combined thermal and moisture convection and entropy generation in an inclined rectangular enclosure partially saturated with porous wall: Nonlinear effects with Soret and Dufour numbers,” International Journal of Mechanical Sciences, Vol. 199, p. 106412, Jun. 2021, https://doi.org/10.1016/j.ijmecsci.2021.106412
-
A. A. Yinusa, M. G. Sobamowo, M. A. Usman, and E. H. Abubakar, “Exploration of three dimensional squeezed flow and heat transfer through a rotating channel with coupled Dufour and Soret influences,” Thermal Science and Engineering Progress, Vol. 21, p. 100788, Mar. 2021, https://doi.org/10.1016/j.tsep.2020.100788
-
Y. Rghif, B. Zeghmati, and F. Bahraoui, “Soret and Dufour effects on thermosolutal convection developed in a salt gradient solar pond,” International Journal of Thermal Sciences, Vol. 161, p. 106760, Mar. 2021, https://doi.org/10.1016/j.ijthermalsci.2020.106760
-
S. Hussain, M. Jamal, and B. P. Geridonmez, “Impact of power law fluid and magnetic field on double diffusive mixed convection in staggered porous cavity considering Dufour and Soret effects,” International Communications in Heat and Mass Transfer, Vol. 121, p. 105075, Feb. 2021, https://doi.org/10.1016/j.icheatmasstransfer.2020.105075
-
S. A. Khan, T. Hayat, and A. Alsaedi, “Irreversibility analysis in Darcy-Forchheimer flow of viscous fluid with Dufour and Soret effects via finite difference method,” Case Studies in Thermal Engineering, Vol. 26, p. 101065, Aug. 2021, https://doi.org/10.1016/j.csite.2021.101065
-
T. Hayat, T. Nasir, M. I. Khan, and A. Alsaedi, “Numerical investigation of MHD flow with Soret and Dufour effect,” Results in Physics, Vol. 8, pp. 1017–1022, Mar. 2018, https://doi.org/10.1016/j.rinp.2018.01.006
-
T. Hayat, S. Asghar, A. Tanveer, and A. Alsaedi, “Chemical reaction in peristaltic motion of MHD couple stress fluid in channel with Soret and Dufour effects,” Results in Physics, Vol. 10, pp. 69–80, Sep. 2018, https://doi.org/10.1016/j.rinp.2018.04.040
-
G. Rasool, A. Shafiq, and D. Baleanu, “Consequences of Soret-Dufour effects, thermal radiation, and binary chemical reaction on darcy forchheimer flow of nanofluids,” Symmetry, Vol. 12, No. 9, p. 1421, Aug. 2020, https://doi.org/10.3390/sym12091421
-
A. H. Usman, Z. Shah, U. W. Humphries, P. Kumam, and P. Thounthong, “Soret, Dufour, and activation energy effects on double diffusive convective couple stress micropolar nanofluid flow in a Hall MHD generator system,” AIP Advances, Vol. 10, No. 7, Jul. 2020, https://doi.org/10.1063/5.0014897
-
P. S. Reddy and A. J. Chamkha, “Soret and Dufour effects on MHD convective flow of Al2O3-water and TiO2-water nanofluids past a stretching sheet in porous media with heat generation/absorption,” Advanced Powder Technology, Vol. 27, No. 4, pp. 1207–1218, Jul. 2016, https://doi.org/10.1016/j.apt.2016.04.005
-
S. Arun and A. Satheesh, “Mesoscopic analysis of MHD double diffusive natural convection and entropy generation in an enclosure filled with liquid metal,” Journal of the Taiwan Institute of Chemical Engineers, Vol. 95, pp. 155–173, Feb. 2019, https://doi.org/10.1016/j.jtice.2018.10.015
-
B. Ali, Y. Nie, S. A. Khan, M. T. Sadiq, and M. Tariq, “Finite element simulation of multiple slip effects on MHD unsteady maxwell nanofluid flow over a permeable stretching sheet with radiation and thermo-diffusion in the presence of chemical reaction,” Processes, Vol. 7, No. 9, p. 628, Sep. 2019, https://doi.org/10.3390/pr7090628
-
M. M. Bhatti and M. M. Rashidi, “Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet,” Journal of Molecular Liquids, Vol. 221, pp. 567–573, Sep. 2016, https://doi.org/10.1016/j.molliq.2016.05.049
-
A. M. Aly, “Natural convection over circular cylinders in a porous enclosure filled with a nanofluid under thermo-diffusion effects,” Journal of the Taiwan Institute of Chemical Engineers, Vol. 70, pp. 88–103, Jan. 2017, https://doi.org/10.1016/j.jtice.2016.10.050
-
M. C. K. Reddy, G. Murali, S. Sivaiah, and N. Babu, “Heat and mass transfer effects on unsteady MHD free convection flow past a vertical permeable moving plate with radiation,” International Journal of Applied Mathematical Research, Vol. 1, No. 2, pp. 189–205, Apr. 2012, https://doi.org/10.14419/ijamr.v1i2.45
-
S. Sivaiah, G. Muraligoud, G. Murali, M. C. K. Reddy, and S. Raju, “Unsteady MHD mixed convection flow past a vertical porous plate in presence of radiation,” International Journal of Basic and Applied Sciences, Vol. 1, No. 4, pp. 651–666, Aug. 2012, https://doi.org/10.14419/ijbas.v1i4.106
-
M. Gundagani, S. Sheri, A. Paul, and M. C. K. Reddy, “Radiation effects on an unsteady MHD convective flow past a semi-infinite vertical permeable moving plate embedded in a porous medium with viscous dissipation,” Walailak Journal of Science and Technology, Vol. 10, No. 5, pp. 499–515, Apr. 2013.
-
D. Gadipally and M. Gundagani, “Analysis of Soret and Dufour effects on unsteady MHD convective flow past a semi-infinite vertical porous plate via finite difference method,” International Journal of Applied Physics and Mathematics, Vol. 4, No. 5, pp. 332–344, 2014, https://doi.org/10.7763/ijapm.2014.v4.306
-
G. Deepa and G. Murali, “Effects of viscous dissipation on unsteady MHD free convective flow with thermophoresis past a radiate inclined permeable plate,” Iranian Journal of Science and Technology (Sciences), Vol. 38, No. 3.1, pp. 379–388, Oct. 2014, https://doi.org/10.22099/ijsts.2014.2437
-
G. Murali, Ajit Paul, and N. V. N. Babu, “Numerical study of chemical reaction effects on unsteady MHD fluid flow past an infinite vertical plate embedded in a porous medium with variable suction,” Electronic Journal of Mathematical Analysis and Applications, Vol. 3, No. 2, Jul. 2015, https://doi.org/10.21608/ejmaa.2015.310762
-
J. A. Khan, M. Mustafa, T. Hayat, M. A. Farooq, A. Alsaedi, and S. J. Liao, “On model for three-dimensional flow of nanofluid: An application to solar energy,” Journal of Molecular Liquids, Vol. 194, pp. 41–47, Jun. 2014, https://doi.org/10.1016/j.molliq.2013.12.045
-
P. Yesodha, M. Bhuvaneswari, S. Sivasankaran, and K. Saravanan, “Convective heat and mass transfer of chemically reacting fluids with activation energy along with Soret and Dufour effects,” Materials Today: Proceedings, Vol. 42, pp. 600–606, 2021, https://doi.org/10.1016/j.matpr.2020.10.878
-
S. Hazarika, S. Ahmed, and A. J. Chamkha, “Investigation of nanoparticles Cu, Ag and Fe3O4 on thermophoresis and viscous dissipation of MHD nanofluid over a stretching sheet in a porous regime: A numerical modeling,” Mathematics and Computers in Simulation, Vol. 182, pp. 819–837, Apr. 2021, https://doi.org/10.1016/j.matcom.2020.12.005
-
M. Shamshuddin, A. Abderrahmane, A. Koulali, M. R. Eid, F. Shahzad, and W. Jamshed, “Thermal and solutal performance of Cu/CuO nanoparticles on a non-linear radially stretching surface with heat source/sink and varying chemical reaction effects,” International Communications in Heat and Mass Transfer, Vol. 129, p. 105710, Dec. 2021, https://doi.org/10.1016/j.icheatmasstransfer.2021.105710
-
S. A. A. Shah, N. A. Ahammad, E. M. T. E. Din, F. Gamaoun, A. U. Awan, and B. Ali, “Bio-convection effects on prandtl hybrid nanofluid flow with chemical reaction and motile microorganism over a stretching sheet,” Nanomaterials, Vol. 12, No. 13, p. 2174, Jun. 2022, https://doi.org/10.3390/nano12132174
-
M. A. Kumar, Y. D. Reddy, B. S. Goud, and V. S. Rao, “An impact on non-Newtonian free convective MHD Casson fluid flow past a vertical porous plate in the existence of Soret, Dufour, and chemical reaction,” International Journal of Ambient Energy, Vol. 43, No. 1, pp. 7410–7418, Dec. 2022, https://doi.org/10.1080/01430750.2022.2063381
Cited by
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
All authors have read and approved the manuscript.
The authors declare that they have no conflict of interest.
