Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory

Youssef, Hamdy M.; Alghamdi, Abdulrahman A.

doi:10.21595/jets.2023.23372

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 26 June 2023

Check for updates

Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory

Hamdy M. Youssef¹

Abdulrahman A. Alghamdi²

¹Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, 21955, Saudi Arabia

²Mathematics Department, College of Applied Sciences, Umm Al-Qura University, Makkah, 21955, Saudi Arabia

Corresponding Author:

Hamdy M. Youssef

Cite the article Download PDF

Abstract

In this work, a novel mathematical model of thermoelastic, homogenous, isotropic, and infinite medium with a spherical cavity has been constructed. Under the hyperbolic two-temperature Green-Naghdi theory of thermoelasticity type-I and type-III with fractional-order strain, the governing equations have been established. The bounding surface of the cavity has been thermally loaded by a ramp-type heat and is connected to a rigid foundation which prevents volumetric strain. Different values of the fractional-order and two-temperature parameters have shown numerical results for the dynamical and conductive temperature increment, strain, displacement, and average of principal stresses, which are graphically applicable to all the functions studied. The fractional-order parameter has significant effects on stress and strain distributions, while it has a limited effect on the dynamical and conductive temperatures increment. The hyperbolic two-temperature parameter has significant effects on all studied functions based on Green-Naghdi models of type-1 and type-II. Moreover, the ramp-time heat parameter has a significant impact on all the studied functions under all the studied models of thermoelasticity.

$Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory$

Highlights

This research examined how skin tissue responds to a steady heat flux caused by a thermo-electrical shock on the bounding plane in terms of temperature reaction and response.
The fractional-order strain parameter significantly affects strain and stress.
The voltage, resistance, and dual-lag time values significantly affect the distribution of temperature increments and the propagation of thermal waves through skin tissue.
The Tzou model is the most effective model that accurately predicts the physical behaviour of skin tissue.
Green-Naghdi type-I thermal wave propagation profiles are smaller than type-III.
Strain reduces mechanical wave propagation profile with a fractional-order and hyperbolic two-temperature heat conduction model.

1. Introduction

How to find a precise model that accurately represents the behaviour of thermoelastic materials is the main issue of the topic. Researchers and writers have created several models that depict how waves are transferred through solids and thermoelastic materials. However, not all of these models are successful because one of the criteria for a good model is to reproduce experimental findings with waves of mechanical and thermal propagation moving at a finite speed. No one field of study can be used to discuss thermomechanical transition models that apply to elastic materials [1].

Based on the idea of fractional calculus, some fresh thermoelastic models were presented. The first model describing the behaviour of the material was created by Magin and Royston using the fractional deformation derivative [2]. The derivative's zero order is a Hookean solid, while it's one order is a Newtonian fluid. The split order of thermoviscoelastic materials and the intermediate heat exchange spectrum [2].

Youssef introduced a different new theory of global thermoelasticity based on the fractional-order strain. It is believed that the connection between stress and strain is a novel and distinctive contribution to Duhamel-Neumann's theory [3]. Youssef has solved the type-II problems of Biot, Lord-Shulman, Green-Lindsay, and thermoelasticity in one dimension with fractional sequence strain [3].

Based on two distinct conductive and dynamic temperatures, Chen and Gurtin created the thermoelasticity model. The relationship between the temperature difference and the heat source [4]. Warren and Chen looked at the propagation of waves in the two-temperature thermoelastic theory [5]. However, there won't be any research on that theory before Youssef updates it and develops a two-temperature generalized thermostat model [6]. Youssef and many other authors applied this concept in several applications and enquiries [7-13]. Youssef and El-Bary validated the two-temperature generalized thermoelasticity model, although it does not give a fixed speed for thermal wave propagation [14]. To replace this model, Youssef and El-Bary created the hyperbolic two-temperature generalized thermoelasticity model, which is based on new thermal conductivity principles [14]. Youssef proposed that the difference between conductive temperature and dynamic temperature acceleration in that model be proportional to the heat supply. In this model, the rate of thermal wave propagation is constrained. Youssef found solutions to several uses of the infinite thermoelastic spherical media [15-18]. In the limitless media, Mukhopadhyay and Kumar investigated the universal thermoelastic interactions with the cavity [19]. Many authors used spherical cavities to solve problems involving thermoelastic mediums [20-29].

In the current work, with a spherical cavity, a novel mathematical model of a thermoelastic, homogenous, isotropic, and infinite medium will be developed. The governing equations will be constructed for the hyperbolic two-temperature Green-Naghdi theory of thermoelasticity type-1 and type-III based on fractional-order strain consideration. A ramp-type heat will thermally load the cavity's boundary, and it is attached to a rigid foundation to avoid volumetric strain. Different fractional-order and two-temperature parameter values will be produced numerical findings for the strain, displacement, average principle stresses, and dynamical and conductive temperature increment, which are visually relevant to all the functions under study.

2. The problem formulation

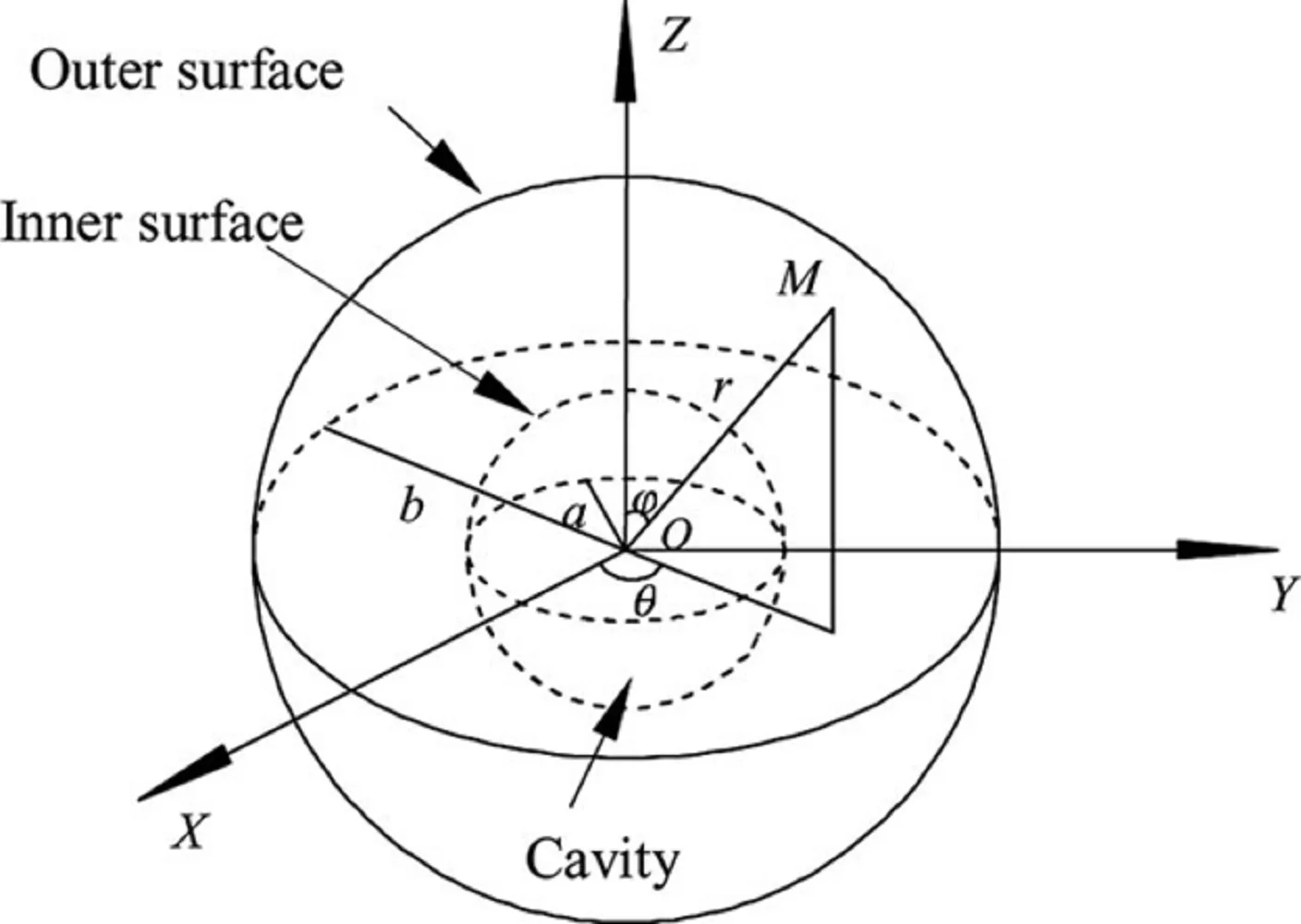
Consider a perfect, thermoelastic, conducting, and isotropic body with a spherical cavity that occupies the region $ξ = \{(r, ψ, ϕ) : a \leq r < \infty, 0 \leq ψ \leq 2 π, 0 \leq ϕ < 2 π\}$ . We use a spherical coordinative system $(r, ψ, ϕ)$ that displays the radial coordinate, co-latitude, and longitude of a spherical system, without any forces on the body and initially calming where r is the sphere radius, as in Fig. 1. When there are no latitude and longitudinal variance is the symmetry condition fulfilled. Both state functions depend on the distance and time of the radius.

Fig. 1The isotropic homogeneous thermoelastic solid sphere with a spherical cavity

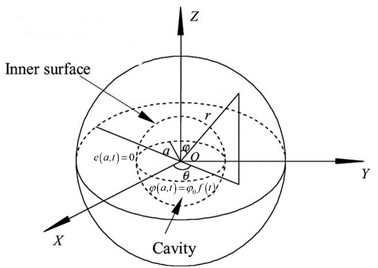
We note that due to spherical symmetry, the displacement components have the form:

1

(u_{r}, u_{ψ}, u_{ϕ}) = (u (r, t), 0,0) .

The equations of motion [3, 13]:

2

ρ \ddot{u} = (λ + 2 μ) (1 + τ^{α} D_{t}^{α}) \frac{\partial e}{\partial r} - γ \frac{\partial T_{D}}{\partial r} .

The constitutive equations with damage mechanics variable [3, 13]:

3

σ_{r r} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{r r} + λ e) - γ (T_{D} - T_{0}),

4

σ_{ψ ψ} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{ψ ψ} + λ e) - γ (T_{D} - T_{0}),

5

σ_{ϕ ϕ} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{ϕ ϕ} + λ e) - γ (T_{D} - T_{0}),

6

σ_{r ϕ} = σ_{ϕ ψ} = σ_{r ψ} = 0 .

The strain components are:

7

e_{r r} = \frac{\partial u}{\partial r}, e_{ψ ψ} = e_{ϕ ϕ} = \frac{u}{r},

and

8

e_{r ϕ} = e_{ϕ ψ} = e_{r ψ} = 0,

where $e$ is the cubical dilatation and is given by:

9

e = e_{r r} + 2 e_{ϕ ϕ} = \frac{\partial u}{\partial r} + \frac{2 u}{r} = \frac{1}{r^{2}} \frac{\partial (r^{2} u)}{\partial r} .

The hyperbolic two-temperature heat conduction equations take the forms [3, 13, 14].

The heat conduction equations which have been proposed by Green-Naghdi take the following form [29]:

10

(\frac{\partial}{\partial t} + \tilde{K}) \nabla^{2} T_{C} = \frac{\partial^{2}}{\partial t^{2}} (\frac{ρ C_{v}}{K} T_{D} + \frac{γ T_{0}}{K} (1 + τ^{α} D_{t}^{α}) e) .

The unified Eq. (6) could be used for the two types of Green-Naghdi theories as follows:

The setting $\tilde{K} = 0$ represents the Green-Naghdi type-I model.

The setting $\tilde{K} = K^{*} / K$ represents the Green-Naghdi type-III model, where $K^{*} = (λ + 2 μ) C_{v} / 4$ is the characteristic of Green-Naghdi theory, $K$ is the usual thermal conductivity, and the unit of the quantity $(\tilde{K})$ is $s^{- 1}$ and:

11

{\ddot{T}}_{C} - {\ddot{T}}_{D} = c^{2} \nabla^{2} T_{C},

where $c$ (m/s) is the hyperbolic two-temperature parameter [14], and $\nabla^{2} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial}{\partial r})$ .

The Riemann – Liouville fractional integral $I^{α} f (t)$ description is used in the above equations written in a convolution-type form [3, 30]:

12

I^{α} f (t) = \frac{1}{Γ (α)} \int_{0}^{t} {(t - υ)}^{α - 1} f (υ) d υ, t > 0, α > 0,

that provides Caputo with the form of fractional derivatives:

13

D_{t}^{α} f (t) = I^{- α} f (t) = \{\begin{array}{l} \frac{1}{Γ (1 - α)} \int_{0}^{t} \frac{f (ξ)}{{(t - ξ)}^{α}} d ξ, & 0 < α < 1, \\ f (t), & α = 0, \\ f^{' (t)}, & α = 1 . \end{array}

We consider that $φ = (T_{C} - T_{0})$ and $θ = (T_{D} - T_{0})$ are the conductive and dynamical temperature increments, respectively. Then the Eqs. (2)-(5), (10) and (11) take the forms:

14

ρ \ddot{u} = (λ + 2 μ) (1 + τ^{α} D_{t}^{α}) \frac{\partial e}{\partial r} - γ \frac{\partial θ}{\partial r},

15

(\frac{\partial}{\partial t} + \tilde{K}) \nabla^{2} φ = \frac{\partial^{2}}{\partial t^{2}} (\frac{ρ C_{v}}{K} θ + \frac{γ T_{0}}{K} (1 + τ^{α} D_{t}^{α}) e),

16

\ddot{φ} - \ddot{θ} = c^{2} \nabla^{2} φ,

17

σ_{r r} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{r r} + λ e) - γ θ,

18

σ_{ψ ψ} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{ψ ψ} + λ e) - γ θ,

19

σ_{ϕ ϕ} = (1 + τ^{α} D_{t}^{α}) (2 μ e_{ϕ ϕ} + λ e) - γ θ,

The Eq. (14) can be re-written to be in the form:

20

\frac{ρ}{(λ + 2 μ)} \ddot{e} = (1 + τ^{α} D_{t}^{α}) \nabla^{2} e - \frac{γ}{(λ + 2 μ)} \nabla^{2} θ .

The following non-dimensional variables are used for convenience [8, 12, 13]:

21

\{r', u', a'\} = c_{o} η \{r, u, a\}, \{t', τ'\} = c_{o}^{2} η \{t, τ\}, \tilde{K'} = \frac{\tilde{K}}{c_{o}^{2} η},

\{θ', φ'\} = \frac{1}{T_{0}} \{θ, φ\}, σ^{'} = \frac{σ}{λ + 2 μ} .

Then, we obtain:

22

\ddot{e} = (1 + τ^{α} D_{t}^{α}) \nabla^{2} e - ε \nabla^{2} θ,

23

(\frac{\partial}{\partial t} + \tilde{K}) \nabla^{2} φ = \frac{\partial^{2}}{\partial t^{2}} (θ + ε_{1} (1 + τ^{α} D_{t}^{α}) e),

24

\ddot{θ} = \ddot{φ} - {\tilde{c}}^{2} \nabla^{2} φ,

25

σ_{r r} = (1 + τ^{α} D_{t}^{α}) (β^{2} e_{r r} + (1 - β^{2}) e) - ε θ,

26

σ_{ψ ψ} = (1 + τ^{α} D_{t}^{α}) (β^{2} e_{ψ ψ} + (1 - β^{2}) e) - ε θ,

27

σ_{ϕ ϕ} = (1 + τ^{α} D_{t}^{α}) (β^{2} e_{ϕ ϕ} + (1 - β^{2}) e) - ε θ .

The prims have been deleted for simplicity.

3. Problem formulation in the Laplace transform domain

The Laplace transform will be applied which is defined as follows:

28

\bar{h} (r; s) = \int_{0}^{\infty} e^{- s t} \bar{h} (r; t) d t,

where the inversion of the Laplace transform may be calculated numerically by the following iteration:

29

h (r; t) = L^{- 1} [\bar{h} (r; s)] \approx \frac{e^{κ t}}{2 t} \bar{h} (r; κ) + \frac{e^{κ t}}{t} R e \sum_{n = 1}^{N} {(- 1)}^{n} \bar{h} (r; \frac{κ t + i n π}{t}),

where $R e$ denotes the real part, while $i$ defines the unit imaginary number. Numerous numerical tests have been conducted to determine if the value of $κ$ may meet the relation $κ t \approx 4.7$ [31, 32].

The Laplace transform of the fractional derivative is defined as [30]:

30

L \{D_{t}^{α} f (t)\} = s^{α} \bar{f} (s) - D_{t}^{α} I^{1 - α} f (0^{+}), 0 < α < 1 .

We assume the following initial conditions:

31

D_{t}^{α} I^{1 - α} \{e (r, 0^{+}), φ (r, 0^{+}), θ (r, 0^{+})\} = 0, 0 < α < 1

32

{{e (r, t)|}_{t = 0} = θ {(r, t)}_{t = 0} = φ {(r, t)}_{t = 0} = \frac{\partial e (r, t)}{\partial t}|}_{t = 0} = {\frac{\partial θ (r, t)}{\partial t}|}_{t = 0} = {\frac{\partial φ (r, t)}{\partial t}|}_{t = 0} = 0 .

Then, we obtain:

33

s^{2} \bar{e} = (1 + τ^{α} s^{α}) \nabla^{2} \bar{e} - ε \nabla^{2} \bar{θ},

34

(s + \tilde{K}) \nabla^{2} \bar{φ} = s^{2} \bar{θ} + ε_{1} s^{2} (1 + τ^{α} s^{α}) \bar{e},

35

s^{2} \bar{θ} = s^{2} \bar{φ} - {\tilde{c}}^{2} \nabla^{2} \bar{φ},

36

{\bar{σ}}_{r r} = (1 + τ^{α} s^{α}) (β^{2} {\bar{e}}_{r r} + (1 - β^{2}) \bar{e}) - ε \bar{θ},

37

{\bar{σ}}_{ψ ψ} = (1 + τ^{α} s^{α}) (β^{2} {\bar{e}}_{ψ ψ} + (1 - β^{2}) \bar{e}) - ε \bar{θ},

38

{\bar{σ}}_{ϕ ϕ} = (1 + τ^{α} s^{α}) (β^{2} {\bar{e}}_{ϕ ϕ} + (1 - β^{2}) \bar{e}) - ε \bar{θ} .

Eliminating $\bar{θ}$ from the Eqs. (33)-(35), we obtain:

39

\nabla^{2} \bar{e} - α_{1} \bar{e} = α_{2} \nabla^{2} \bar{φ} - α_{3} \nabla^{4} \bar{φ},

40

\nabla^{2} \bar{φ} = α_{4} \bar{φ} + α_{5} \bar{e},

where:

α_{1} = \frac{s^{2}}{(1 + τ^{α} s^{α})}, α_{2} = \frac{ε}{(1 + τ^{α} s^{α})}, α_{3} = \frac{{\tilde{c}}^{2} ε}{s^{2} (1 + τ^{α} s^{α})},

α_{4} = \frac{s^{2}}{(s + \tilde{K} + {\tilde{c}}^{2})}, α_{5} = \frac{ε_{1} s^{2} (1 + τ^{α} s^{α})}{(s + \tilde{K} + {\tilde{c}}^{2})} .

Eliminating $\bar{e}$ from the Eqs. (38) and (39), we get:

41

[\nabla^{4} - L \nabla^{2} + M] \bar{φ} = (\nabla^{2} - k_{1}^{2}) (\nabla^{2} - k_{2}^{2}) \bar{φ} = 0 .

Eliminating $\bar{φ}$ from the Eqs. (39) and (40), we obtain:

42

[\nabla^{4} - L \nabla^{2} + M] \bar{e} = (\nabla^{2} - k_{1}^{2}) (\nabla^{2} - k_{2}^{2}) \bar{e} = 0,

where $L = \frac{(α_{1} + α_{4} + α_{2} α_{5})}{(1 + α_{3} α_{5})}$ , $M = \frac{α_{1} α_{4}}{(1 + α_{3} α_{5})}$ , and $\pm k_{1}, \pm k_{2}$ are the roots of the following characteristic equation:

43

k^{4} - L k^{2} + M = 0 .

The general solutions of the Eqs. (41) and (42) must be bounded at infinity, thus, they take the following forms:

44

\bar{φ} (r, s) = A_{1} \frac{e^{- k_{1} r}}{r} + A_{2} \frac{e^{- k_{2} r}}{r}, a \leq r < \infty,

45

\bar{e} (r, s) = B_{1} \frac{e^{- k_{1} r}}{r} + B_{2} \frac{e^{- k_{2} r}}{r}, a \leq r < \infty .

From the Eq. (39), we obtain:

46

(k_{i}^{2} - α_{4}) A_{i} = α_{5} B_{i}, i = 1,2 .

Thus, we have:

47

\bar{e} (r, s) = (k_{1}^{2} - α_{4}) A_{1} \frac{e^{- k_{1} r}}{α_{5} r} + (k_{2}^{2} - α_{4}) A_{2} \frac{e^{- k_{2} r}}{α_{5} r}, a \leq r < \infty .

To get the parameters $A_{1}$ and $A_{2}$ , we must apply the boundary conditions, so we will consider that the surface of the cavity is subjected to a thermal loading with a function of time only as follows:

48

φ (a, t) = φ_{0} f (t) .

Moreover, we will consider that the surface of the cavity is connected to a rigid foundation which can stop any cubical deformation, i.e., we have:

49

e (a, t) = 0 .

After applying Laplace transform, we obtain:

50

\bar{φ} (a, s) = φ_{0} \bar{f} (s),

51

\bar{e} (a, s) = 0 .

By using the conditions Eqs. (50) and (51) into the Eqs. (44) and (47), we obtain the following system of linear equations:

52

A_{1} e^{- k_{1} a} + A_{2} e^{- k_{2} a} = a φ_{0} \bar{f} (s),

53

(k_{1}^{2} - α_{4}) A_{1} e^{- k_{1} a} + (k_{2}^{2} - α_{4}) A_{1} e^{- k_{2} a} = 0 .

By solving the above system, we get:

54

A_{1} = \frac{(k_{2}^{2} - α_{4}) a φ_{0} \bar{f} (s)}{k_{2}^{2} - k_{1}^{2}} e^{k_{1} a}, A_{2} = - \frac{(k_{1}^{2} - α_{4}) a φ_{0} \bar{f} (s)}{k_{2}^{2} - k_{1}^{2}} e^{k_{2} a} .

Hence, we have the solutions in the Laplace transform domain as follows:

55

\bar{φ} (r, s) = \frac{a φ_{0} \bar{f} (s)}{k_{2}^{2} - k_{1}^{2}} [(k_{2}^{2} - α_{4}) \frac{e^{- k_{1} (r - a)}}{r} - (k_{1}^{2} - α_{4}) \frac{e^{- k_{2} (r - a)}}{r}], a \leq r < \infty,

56

\bar{e} (r, s) = \frac{(k_{1}^{2} - α_{4}) (k_{2}^{2} - α_{4}) a φ_{0} \bar{f} (s)}{α_{5} (k_{2}^{2} - k_{1}^{2})} (\frac{e^{- k_{1} (r - a)}}{r} - \frac{e^{- k_{2} (r - a)}}{r}), a \leq r < \infty .

Now, we must determine the thermal loading function $f (t)$ , so we will consider that the thermal loading function is a ramp-type heating which takes the form [7, 33, 34]:

57

f (t) = \{\begin{array}{l} \frac{t}{t_{0}}, & 0 < t < t_{0}, \\ 1, & t \geq t_{0}, \end{array}

where $t_{0}$ is called the ramp-time heat parameter.

After applying the Laplace transform to the above equation, we obtain:

58

\bar{f} (s) = \frac{1 - e^{- t_{0} s}}{t_{0} s^{2}} .

That completes the solutions in the Laplace transform domain.

To obtain the stress distribution, we can sum the Eq. (35)-(37), then we obtain the average value of the principal stresses components as follows:

59

σ_{a v g} = \frac{{\bar{σ}}_{r r} + {\bar{σ}}_{ψ ψ} + {\bar{σ}}_{ϕ ϕ}}{3} = (1 + τ^{α} s^{α}) (1 - \frac{2}{3} β^{2}) \bar{e} - ε \bar{θ} .

4. Numerical results

For the numerical results, silicon (Si) has been taken as the thermoelastic semiconducting material, for which we take the following values of the different physical constants [7, 33-35]: $μ =$ 5.46×10¹⁰ kg m^-1 s^-2, $λ =$ 3.64×10¹⁰ kg m^-1 s^-2, $ρ =$ 2330 kg m^-3, $C_{v} =$ 695 m² K^-1 s^-2, $α_{T} =$ 3.0×10^-6 K^-1, $K =$ 150 kg m k^-1 s^-3, $φ_{0} =$ 1.0.

The numerical results of the dynamic temperature increment, conductive temperature increment, volumetric deformation, displacement, average stress, and stress-strain energy distributions have been figured with a wide range of the dimensionless radial distance $r (1 \leq r \leq 4)$ and at the instant value of dimensionless time $t =$ 1.0.

5. Discussions

Figs. 2 and 3 show the studied function distributions of Green-Naghdi type-I and type-III, respectively, with various values of the fractional-order parameter $α =$ (0.0, 0.4, 0.6, 0,9) at a time $t = 2.0$ and $t_{0} = 2.0$ to sand on the effect of the fractional-order parameter.

Fig. 2The studied function distributions of Green-Naghdi type-I with various values of the fractional-order parameter

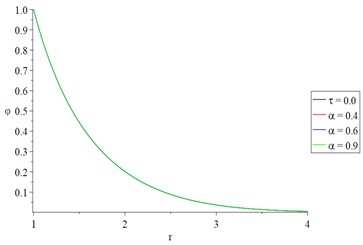
$The studied function distributions of Green-Naghdi type-I with various values of the fractional-order parameter$

a) The conductive temperature increment

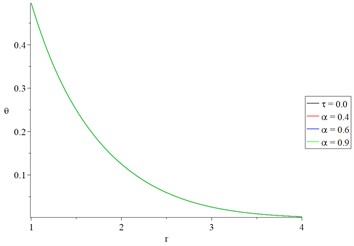
$The studied function distributions of Green-Naghdi type-I with various values of the fractional-order parameter$

b) The dynamic temperature increment

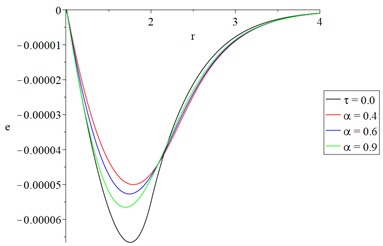
$The studied function distributions of Green-Naghdi type-I with various values of the fractional-order parameter$

c) The volumetric strain

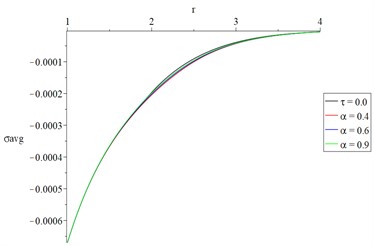
$The studied function distributions of Green-Naghdi type-I with various values of the fractional-order parameter$

d) The average of principal stresses

Fig. 2(a), 3(a), 2(b), and 3(b) represent the conductive and dynamical temperature increments, respectively. It is noted that the value of the fractional-order strain parameter has a very limited effect on the thermal wave.

Figs. 2(c) and 3(c) represent the volumetric strain, and it is noted that the fractional-order of strain parameter has a significant effect where the absolute value of the peak point of the volumetric strain increases when the value of the fractional-order strain parameter increases. Moreover, the maximum absolute value of the volumetric strain occurs when the consideration of the fractional-order strain does not exist.

Figs. 2(d) and 3(d) represent the average value of the principal stresses, and it is noted that the fractional-order of strain parameter has a small effect.

Also, we can see that the value of the dynamical temperature increment based on type-I is smaller than its value based on type-III. While the absolute value of the principal stresses based on type-I is greater than its value based on type-III.

Figs. 4 and 5 show the studied functions distributions of Green-Naghdi type-I and type-II, respectively, based on one-temperature and hyperbolic two-temperature models ( $c =$ 0.0 and $c \neq$ 0.0) and various values of the fractional-order parameter $α =$ (0.0, 0.5) at a time $t =$ 2.0 and $t_{0} =$ 2.0 to sand on the effect of the fractional-order parameter on the two studied models.

Figs 4(a), 4(b), 5(a), and 5(d) show that the hyperbolic two-temperature parameter has significant effects on the conductive and dynamical temperature increment or the thermal wave in general for the two studied types I and III.

Fig. 3The studied function distributions of Green-Naghdi type-III with various values of the fractional-order parameter

$The studied function distributions of Green-Naghdi type-III with various values of the fractional-order parameter$

a) The conductive temperature increment

$The studied function distributions of Green-Naghdi type-III with various values of the fractional-order parameter$

b) The dynamic temperature increment.

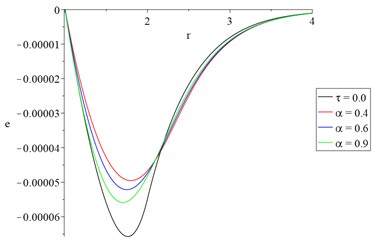
$The studied function distributions of Green-Naghdi type-III with various values of the fractional-order parameter$

c) The volumetric strain

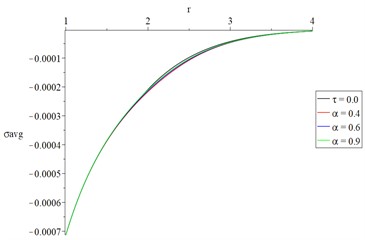
$The studied function distributions of Green-Naghdi type-III with various values of the fractional-order parameter$

d) The average of principal stresses

Fig. 4The studied functions distributions of Green-Naghdi type-I based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter

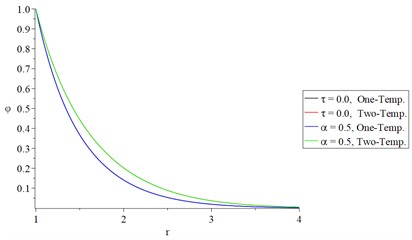
$The studied functions distributions of Green-Naghdi type-I based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

a) The conductive temperature increment

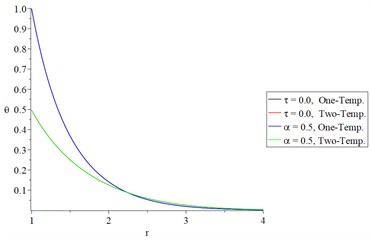
$The studied functions distributions of Green-Naghdi type-I based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

b) The dynamic temperature increment.

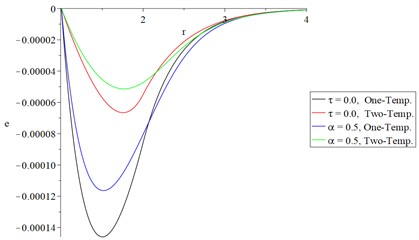
$The studied functions distributions of Green-Naghdi type-I based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

c) The volumetric strain

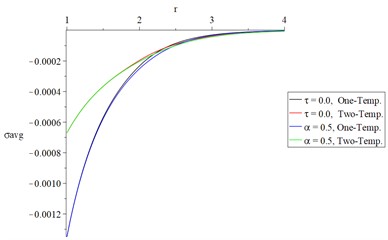
$The studied functions distributions of Green-Naghdi type-I based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

d) The average of principal stresses

Figs. 4(c) and 5(c) represent the volumetric strain distributions, and it is noted that the hyperbolic two-temperature parameter has a significant effect beside the fractional-order strain parameter where the absolute value of the peak point of the volumetric strain for the two studied types take the following order:

60

e^{M a x} (τ = 0.0, O n e - T e m p .) > e^{M a x} (τ \neq 0, O n e - T e m p .) > e^{M a x} (τ = 0.0, T w o - T e m p .) > e^{M a x} (τ \neq 0, T w o - T e m p .)

The above equation indicates that considering strain with fractional-order and hyperbolic two-temperature heat model leads to a decrease in the profile of the mechanical wave propagation.

Figs. 4(d) and 5(d) represent the average of principal stresses distributions, and it is noted that the two-temperature parameter has a significant effect besides the fractional-order strain parameter.

Fig. 5The studied functions distributions of Green-Naghdi type-III based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter

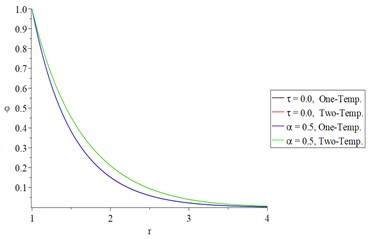
$The studied functions distributions of Green-Naghdi type-III based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

a) The conductive temperature increment

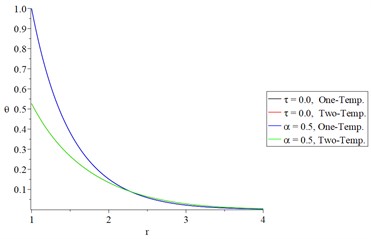
$The studied functions distributions of Green-Naghdi type-III based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

b) The dynamic temperature increment

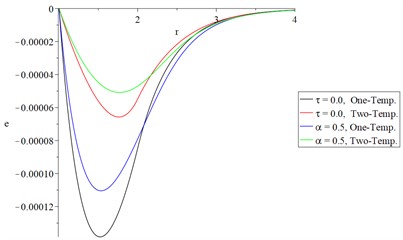
$The studied functions distributions of Green-Naghdi type-III based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

c) The volumetric strain

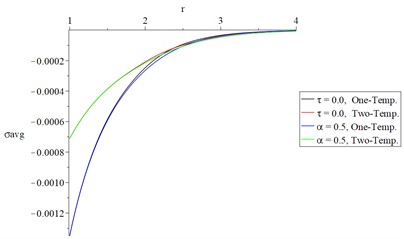
$The studied functions distributions of Green-Naghdi type-III based on one-temperature and hyperbolic two-temperature and various values of the fractional-order parameter$

d) The average of principal stresses

Figs. 6 and 7 show the studied functions distributions of Green-Naghdi type-I and type-II, respectively, based on one-temperature and hyperbolic two-temperature models ( $c =$ 0.0 and $c \neq$ 0.0) and the fractional-order parameter $α = 0.5$ when $t < t_{0}$ and $t > t_{0}$ , respectively to stand on the effect of the ramp-time heat parameter on all the studied functions.

Figs. 6(a), 6(b), 7(a), and 7(b) show that the ramp-time heat parameter has significant effects on the conductive and dynamical temperature increments. Based on the case $t < t_{0}$ , the profile of the thermal wave’s propagation is smaller than its propagation based on the case $t > t_{0}$ in the context of one-temperature and hyperbolic two-temperature models of Green-Naghdi type-I and type-III.

Figs. 6(c), 6(d), 7(c), and 7(d) show that the ramp-time heat parameter has significant effects on the volumetric strain and average of principal stresses. Based on the case $t < t_{0}$ , the absolute value of the volumetric strain and average of principal stresses (the profile of the mechanical wave’s propagation) are smaller based on the case $t > t_{0}$ in the context of one-temperature and hyperbolic two-temperature models of Green-Naghdi type-I and type-III.

Fig. 6The studied functions distributions of Green-Naghdi Type-I and type-III based on one-/two-temperature when α=0.5 and t<t0

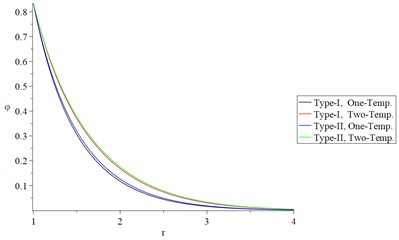
a) The conductive temperature increment

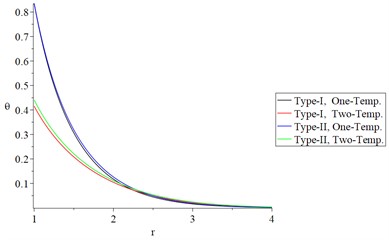
b) The dynamic temperature increment.

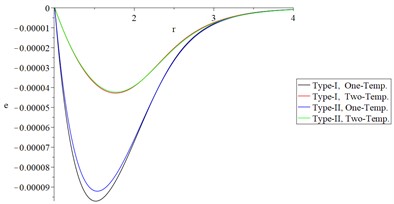
c) The volumetric strain

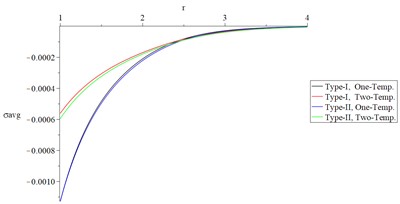
d) The average of principal stresses

Fig. 7The studied functions distributions of Green-Naghdi Type-I and type-III based on one-/two-temperature when α=0.5 and t>t0

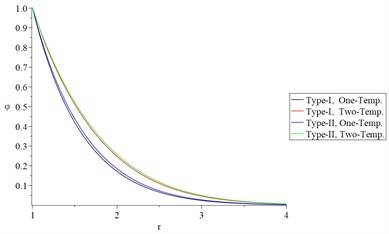
a) The conductive temperature increment

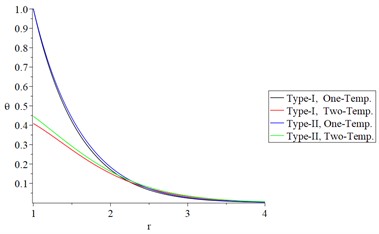
b) The dynamic temperature increment.

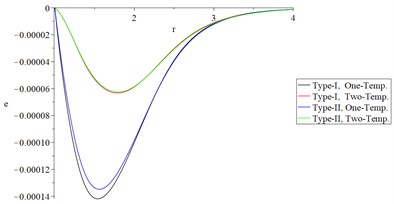
c) The volumetric strain

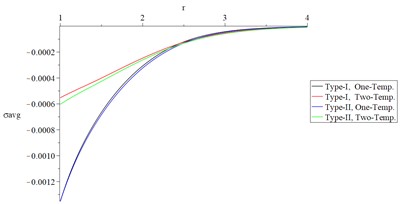
d) The average of principal stresses

6. Conclusions

1) The value of the fractional-order strain parameter has limited effects on the conductive and dynamical temperature increments.

2) The value of the fractional-order strain parameter has significant effects on strain and stress.

3) The hyperbolic two-temperature parameter has significant effects on the conductive and dynamical temperature increments, strain, and stress.

4) The ramp-time heat parameter has significant effects on the conductive and dynamical temperature increments, strain, and stress.

5) The profile of the thermal wave’s propagation based on Green-Naghdi type-I is smaller based on Green-Naghdi type-III.

6) The profile of the mechanical wave’s propagation based on Green-Naghdi type-I is greater based on Green-Naghdi type-III.

7) Considering strain with a fractional-order and hyperbolic two-temperature heat conduction model causes the profile of mechanical wave propagation to be reduced.

8) Green-Naghdi type-I and type-II based on hyperbolic two-temperature heat conduction models offer propagation of thermal and mechanical waves with finite speeds.

References

H. M. Youssef, A. A. El-Bary, and E. A. N. Al-Lehaibi, “The fractional strain influence on a solid sphere under hyperbolic two-temperature generalized thermoelasticity theory by using diagonalization method,” Mathematical Problems in Engineering, Vol. 2021, pp. 1–12, Feb. 2021, https://doi.org/10.1155/2021/6644133

Publisher
R. L. Magin and T. J. Royston, “Fractional-order elastic models of cartilage: A multi-scale approach,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 3, pp. 657–664, Mar. 2010, https://doi.org/10.1016/j.cnsns.2009.05.008

Publisher
H. M. Youssef, “Theory of generalized thermoelasticity with fractional order strain,” Journal of Vibration and Control, Vol. 22, No. 18, pp. 3840–3857, Oct. 2016, https://doi.org/10.1177/1077546314566837

Publisher
P. J. Chen and M. E. Gurtin, “On a theory of heat conduction involving two temperatures,” Zeitschrift für angewandte Mathematik und Physik ZAMP, Vol. 19, No. 4, pp. 614–627, Jul. 1968, https://doi.org/10.1007/bf01594969

Publisher
W. E. Warren and P. J. Chen, “Wave propagation in the two temperature theory of thermoelasticity,” Acta Mechanica, Vol. 16, No. 1-2, pp. 21–33, Mar. 1973, https://doi.org/10.1007/bf01177123

Publisher
H. M. Youssef, “Theory of two-temperature-generalized thermoelasticity,” IMA Journal of Applied Mathematics, Vol. 71, No. 3, pp. 383–390, Jun. 2006, https://doi.org/10.1093/imamat/hxh101

Publisher
I. A. Abbas and H. M. Youssef, “Two-temperature generalized thermoelasticity under ramp-type heating by finite element method,” Meccanica, Vol. 48, No. 2, pp. 331–339, Mar. 2013, https://doi.org/10.1007/s11012-012-9604-8

Publisher
H. Youssef, “Two-temperature generalized thermoelastic infinite medium with cylindrical cavity subjected to different types of thermal loading,” WSEAS Transactions on Heat and Mass Transfer, Vol. 1, No. 10, p. 769, 2006.

Search CrossRef
H. Youssef, “A two-temperature generalized thermoelastic medium subjected to a moving heat source and ramp-type heating: a state-space approach,” Journal of Mechanics of Materials and Structures, Vol. 4, No. 9, pp. 1637–1649, 2010.

Publisher
A. A. El-Bary, H. M. Youssef, and M. A. E. Nasr, “Hyperbolic two-temperature generalized thermoelastic infinite medium with cylindrical cavity subjected to the non-Gaussian laser beam,” Journal of Umm Al-Qura University for Engineering and Architecture, Vol. 13, No. 1-2, pp. 62–69, Dec. 2022, https://doi.org/https://doi.org/10.1007/s43995-022-00004-y

Publisher
H. M. Youssef, “Two-dimensional problem of a two-temperature generalized thermoelastic half-space subjected to ramp-type heating,” Computational Mathematics and Modeling, Vol. 19, No. 2, pp. 201–216, Apr. 2008, https://doi.org/10.1007/s10598-008-0014-7

Publisher
H. M. Youssef, “Two-temperature generalized thermoelastic infinite medium with cylindrical cavity subjected to moving heat source,” Archive of Applied Mechanics, Vol. 80, No. 11, pp. 1213–1224, Nov. 2010, https://doi.org/10.1007/s00419-009-0359-1

Publisher
H. M. Youssef and A. A. El-Bary, “Characterization of the photothermal interaction of a semiconducting solid sphere due to the fractional deformation, relaxation time, and various reference temperature under L-S theory,” Silicon, Vol. 13, No. 7, pp. 2103–2114, Jul. 2021, https://doi.org/10.1007/s12633-020-00631-x

Publisher
H. M. Youssef and A. A. El-Bary, “Theory of hyperbolic two-temperature generalized thermoelasticity,” Materials Physics and Mechanics, Vol. 40, pp. 158–171, 2018.

Search CrossRef
H. Youssef, “State-space approach on generalized thermoelasticity for an infinite material with a spherical cavity and variable thermal conductivity subjected to ramp-type heating,” Canadian Applied Mathematics Quarterly, Vol. 13, 2005.

Search CrossRef
H. M. Youssef, “Dependence of modulus of elasticity and thermal conductivity on reference temperature in generalized thermoelasticity for an infinite material with a spherical cavity,” Applied Mathematics and Mechanics, Vol. 26, No. 4, pp. 470–475, Apr. 2005, https://doi.org/10.1007/bf02465386

Publisher
H. M. Youssef and A. H. Al-Harby, “State-space approach of two-temperature generalized thermoelasticity of infinite body with a spherical cavity subjected to different types of thermal loading,” Archive of Applied Mechanics, Vol. 77, No. 9, pp. 675–687, Jul. 2007, https://doi.org/10.1007/s00419-007-0120-6

Publisher
H. M. Youssef, “Generalized thermoelastic infinite medium with spherical cavity subjected to moving heat source,” Computational Mathematics and Modeling, Vol. 21, No. 2, pp. 212–225, Apr. 2010, https://doi.org/10.1007/s10598-010-9066-6

Publisher
S. Mukhopadhyay and R. Kumar, “A study of generalized thermoelastic interactions in an unbounded medium with a spherical cavity,” Computers and Mathematics with Applications, Vol. 56, No. 9, pp. 2329–2339, Nov. 2008, https://doi.org/10.1016/j.camwa.2008.05.031

Publisher
M. A. K. Molla, N. Mondal, and S. H. Mallik, “Effects of fractional and two-temperature parameters on stress distributions for an unbounded generalized thermoelastic medium with spherical cavity,” Arab Journal of Basic and Applied Sciences, Vol. 26, No. 1, pp. 302–310, 2019.

Publisher
S. Mondal and A. Sur, “Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses,” Waves in Random and Complex Media, Vol. 31, No. 6, pp. 1835–1858, Nov. 2021, https://doi.org/10.1080/17455030.2019.1705426

Publisher
Eman A. N. Al-Lehaibi, “Mathematical model of generalized thermoelastic infinite medium with a spherical cavity and fractional order strain,” Journal of Nonlinear Sciences and Applications, Vol. 12, No. 1, 2018.

Publisher
W. Peng, Y. Ma, C. Li, and T. He, “Dynamic analysis to the fractional order thermoelastic diffusion problem of an infinite body with a spherical cavity and variable material properties,” Journal of Thermal Stresses, Vol. 43, No. 1, pp. 38–54, 2020.

Publisher
M. Othman, Elsayed M. Abd‐Elaziz, and Mohamed I. M. Hilal, “State-space approach to a 2-D generalized thermoelastic medium under the effect of inclined load and gravity using a dual-phase-lag model,” Mechanics Based Design of Structures and Machines, pp. 1–17, 2020.

Publisher
H. Sherief and Eman M. Hussein, “The effect of fractional thermoelasticity on two-dimensional problems in spherical regions under axisymmetric distributions,” Journal of Thermal Stresses, Vol. 43, No. 4, pp. 440–455, 2020.

Publisher
S. Biswas, “Thermoelastic interaction in unbounded transversely isotropic medium containing spherical cavity with energy dissipation,” Indian Journal of Physics, Vol. 95, No. 4, pp. 705–716, Apr. 2021, https://doi.org/10.1007/s12648-020-01705-7

Publisher
D. K. Sharma, M. Bachher, and N. Sarkar, “Effect of phase-lags on the transient waves in an axisymmetric functionally graded viscothermoelastic spherical cavity in radial direction,” International Journal of Dynamics and Control, Vol. 9, No. 2, pp. 424–437, Jun. 2021, https://doi.org/10.1007/s40435-020-00659-2

Publisher
P. Lata and H. Kaur, “Effect of two temperature on isotropic modified couple stress thermoelastic medium with and without energy dissipation,” Geomechanics and Engineering, Vol. 21, No. 5, pp. 461–469, Jun. 2020, https://doi.org/10.12989/gae.2020.21.5.461

Publisher
Eman M. Hussein, “Two dimensional spherical regions problem in the context of the theory of generalized thermoelastic diffusion,” Journal of Thermal Stresses, pp. 1–15, 2020.

Publisher
Y. Povstenko, “Fractional Thermoelasticity,” in Encyclopedia of Thermal Stresses, Dordrecht: Springer Netherlands, 2014, pp. 1778–1787, https://doi.org/10.1007/978-94-007-2739-7_612

Publisher
D. Y. Tzou, “On the thermal shock wave induced by a moving heat source,” Journal of Heat Transfer, Vol. 111, No. 2, pp. 232–238, May 1989, https://doi.org/10.1115/1.3250667

Publisher
D. Tzou, Transfer M-tMH: The Lagging Behavior. Washington: Taylor Francis, 1997.

Search CrossRef
H. Youssef and A. El-Bary, “Generalized magneto-thermoelastic medium with variable material properties subjected to ramp-type heating,” Journal of Applied Polymer Science, Vol. 124, No. 6, pp. 5209–5219, 2011.

Publisher
H. M. Youssef and E. A. Al-Lehaibi, “Fractional order generalized thermoelastic half-space subjected to ramp-type heating,” Mechanics Research Communications, Vol. 37, No. 5, pp. 448–452, Jul. 2010, https://doi.org/10.1016/j.mechrescom.2010.06.003

Publisher
M. A. Hopcroft, W. D. Nix, and T. W. Kenny, “What is the Young’s Modulus of Silicon?,” Journal of Microelectromechanical Systems, Vol. 19, No. 2, pp. 229–238, 2010.

Publisher

About this article

Received

04 May 2023

Accepted

08 June 2023

Published

26 June 2023

DOI

https://doi.org/10.21595/jets.2023.23372

Keywords

hyperbolic two-temperature

Green-Naghdi

spherical cavity

fractional-order strain

ramp-type heat

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Youssef construct the model, consider the conditions, obtain the numerical solutions, review all the work, and submit for publishing. Alghamdi figure the numerical results, discuss the results, set the conclusion, and write all the work.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2022 06 30

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Hamdy M. Youssef, Abdullah A. Al Thobaiti

Research article

2021 09 13

Hyperbolic two-temperature generalized thermoelasticity with fractional order strain of solid cylinder

Alaa A. El-Bary

Research article

2021 06 30

Thermal shock problem of a generalized thermoelastic solid sphere affected by mechanical damage and thermal diffusion

Hamdy M. Youssef

Research article

2019 09 30

Thermal shock behaviour on generalized thermoelastic semi-infinite medium with moving heat source under Green Naghdi-III model

Biswajit Singh, Smita Pal (Sarkar)

H. M. Youssef and A. A. Alghamdi, “Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory,” Journal of Engineering and Thermal Sciences, Vol. 3, No. 1, pp. 11–24, Jun. 2023, https://doi.org/10.21595/jets.2023.23372

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2023.23372
UR  - https://doi.org/10.21595/jets.2023.23372
TI  - Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory
T2  - Journal of Engineering and Thermal Sciences
AU  - Youssef, Hamdy M.
AU  - Alghamdi, Abdulrahman A.
PY  - 2023
DA  - 2023/06/26
PB  - JVE International Ltd.
SP  - 11-24
VL  - 3
IS  - 1
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Youssef_2023,
	doi = {10.21595/jets.2023.23372},
	url = {https://doi.org/10.21595/jets.2023.23372},
	year = 2023,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {3},
	number = {1},
	pages = {11--24},
	author = {Hamdy M. Youssef and Abdulrahman A. Alghamdi},
	title = {Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]H. M. Youssef and A. A. Alghamdi, “Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory,” Journal of Engineering and Thermal Sciences, vol. 3, no. 1, pp. 11–24, Jun. 2023, doi: 10.21595/jets.2023.23372.

Copy IEEE

Copied to clipboard!

Youssef, Hamdy M., and Abdulrahman A. Alghamdi. “Influence of the Fractional-Order Strain on an Infinite Material with a Spherical Cavity under Green-Naghdi Hyperbolic Two-Temperature Thermoelasticity Theory.” Journal of Engineering and Thermal Sciences 3, no. 1 (June 26, 2023): 11–24. https://doi.org/10.21595/jets.2023.23372.

Copy Chicago

Copied to clipboard!

Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory

Abstract

Highlights

1. Introduction

2. The problem formulation

3. Problem formulation in the Laplace transform domain

4. Numerical results

5. Discussions

6. Conclusions

References

About this article

Related Articles