Hyperbolic two-temperature generalized thermoelasticity with fractional order strain of solid cylinder

1. Introduction

Finding the best mathematical model that simulates the behavior of these materials close to experience is one of the key problems in materials and solid sciences. The mathematical model produces results that are completely consistent with experimental findings, and researchers in this area are primarily interested in the physical behavior of these compounds. Various mathematical models have been proposed by scientists and researchers to explain the propagation of mechanical waves and heat in solid and elastic materials. However, not all these models are suitable, since one of the metrics of an ideal model is to include the speed of progression of mechanical and thermal waves with finite values as experimental results. Mathematical models of thermomechanical transformation through elastic materials involve a large amount of space that cannot be included in a single study. However, new models that seek to demonstrate new observations that are very close to laboratory studies and are generally consistent with the physical behavior of thermo-elastic materials should be discussed.

Chen and Gurtin [1] have introduced a thermoelastic theory based on two different temperatures, conductive and dynamic temperature. The difference between these two temperatures is proportional to the heat source. Warren and Chen [2] studied wave propagation in the two-temperature thermo-elasticity principle. However, there is no investigation of this theory until Youssef [3] has updated this theory and introduced a two-temperature generalized thermo-elasticity model. Youssef and Elsibai enhanced the two-temperature thermoelasticity principle without a Green-Naghdi model energy dissipation [4]. Youssef and many other authors have used this model in many applications and research [5-8]. Youssef and El-Bary approved that the two-temperature generalized thermoelasticity model does not provide a finite speed of propagation of the thermal waves [9]. Youssef and El-Bary have therefore updated the model and have introduced a new two-temperature model based on different heat piping rules, known as hyperbolic, generalized 2-temperature thermoelasticity [9].

Youssef suggested in this model that the difference between the conductive temperature acceleration and the acceleration of the thermal temperature during the material transition is proportionate to the heater supply. The speed of the spread of thermal waves is limited within this model.

Additional new models of thermoelasticity based on the fractional calculus principle were introduced. Magin and Royston [10] have introduced the first model that applies the fractional deformation derivative characterizing the material's behavior. The zero-order of the derivative is for a Hookean solid while the one-order is for a Newtonian fluid. The thermoelastic and thermoviscoelastic materials are sitting in the intermediate range with a fractional order parameter between zero and one [10]. C Li et al. studied the generalized thermoelastic diffusion problems with fractional-order strain [11, 12]. Li, Chenlin, et al. studied the generalized piezoelectric thermoelasticity problems with strain rate and transient thermo‐electromechanical responses analysis [13].

Recently, many applications used the fractional-order definition with various construction and different models [14-22]. Depending on the fractional strain, Youssef [23] presented another new theory of generalized thermoelectricity. It is seen as another shift in the stress-strain relationship between Duhamel and Neumann. Youssef solved an application of thermoelasticity with fractional order strain for a one-dimensional half-space, in the context of models of Biot, Lord-Shulman, Green-Lindsay, and Green-Naghdi type II [23]. Youssef solved many applications of thermoelasticity of infinite thermoelastic cylindrical medium [8, 24].

In the present investigation, we will study the induced conductive temperature, dynamic temperature, deformation, displacement, and stress fields in a thermoelastic one-dimensional infinite cylindrical body. The work under the purview of the theory of thermoelasticity with fraction order strain is based on hyperbolic two-temperature heat conduction laws.

The main target of this work is to discuss and study the effects of the fractional-order strain parameter and hyperbolic two-temperature parameter on thermomechanical waves through a thermoelastic body.

2. The governing equations

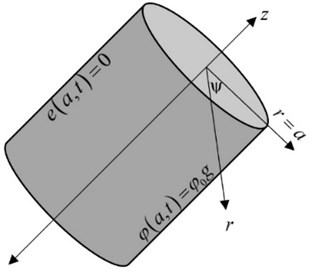
Consider a perfect thermal conducting, isotropic, elastic, and cylindrical body occupies the region $\mathrm{\Lambda }=\left\{\left(r,\psi ,z\right):0\le r\le a,0\le \psi \le 2\pi ,0\le z<\infty \right\}$. We apply a cylindrical coordinates system $\left(r,\psi ,z;t\right)$ in which the $z$-axis was lying along the axis of the cylinder, as in Fig. 1, and due to symmetry, the medium is one-dimensional. Moreover, all the state-functions will depend on the radial distance $r$ and the time $t$. It is proposed that there are no body forces or heat sources in the medium and initially at rest.

Thus, the governing equations in cylindrical one-dimensional with fractional order strain can be written as [8, 24].

The equation of motion:

The heat equation:

where $c$(m/s) is constant (two-temperature parameter).

Fig. 1The isotropic homogeneous thermoelastic solid cylinder

The constitutive relations will take the forms:

and $e$ is the volume dilatation and satisfies the relation:

where ${\nabla }^2=\frac{\partial {}^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}$.

In the above equations, we apply the definition of the Riemann–Liouville fractional integral $I^{\alpha }f\left(t\right)$ written in a convolution type form :[25]

which gives Caputo fractional derivatives in the form:

For convenience, we will use the following non-dimensional variables [8, 24]:

where $c_o^2=\frac{\lambda +2\mu }{\rho }$ and $\eta =\frac{\rho C_E}{K}$.

Eqs. (1)-(6) take the following forms (the primes are suppressed for simplicity):

where $\gamma =\left(3\lambda +2\mu \right){\alpha }_T$, ${\epsilon }_1=\frac{\gamma T_o}{\mu }$, $\epsilon =\frac{\gamma }{\rho C_E}$, $\beta ={\left(\frac{\lambda +2\mu }{\mu }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, $b=\frac{{\epsilon }_1}{{\beta }^2}$, ${\tilde{c}}^2=\frac{c^2}{c_o^2}$.

We apply the Laplace transform defined as:

The Laplace transform of the fractional derivative is defined as [25]:

We assume the following initial conditions:

Thus, the Eqs. (12)-(17) have the forms:

where ${\delta }^2={\tilde{c}}^2/s^2$.

We can re-write Eqs. (22)-(24) in the forms:

where ${\alpha }_1=\frac{b}{\left(1+{\tau }^{\alpha }{s}^{\alpha }\right)}$, ${\alpha }_2=\frac{s^2}{\left(1+{\tau }^{\alpha }{s}^{\alpha }\right)}$, ${\alpha }_3=\left(s+{\tau }_o{s}^2\right)$, ${\alpha }_4=\epsilon \left(s+{\tau }_o{s}^2\right)\left(1+{\tau }^{\alpha }{s}^{\alpha }\right)$.

By inserting Eq. (31) into the Eq. (29), we obtain:

Substitute from Eq. (31) into the Eq. (30), we get:

where ${\alpha }_5=\frac{{\alpha }_3}{\left(1+{\alpha }_3{\delta }^2\right)}$ and ${\alpha }_6=\frac{{\alpha }_4}{\left(1+{\alpha }_3{\delta }^2\right)}$.

Substitute from Eq. (33) into the Eq. (31), we get:

where ${\alpha }_7=\left(1-{\delta }^2{\alpha }_5\right)$ and ${\alpha }_8={\delta }^2{\alpha }_6$.

By eliminating $\stackrel{-}{e}$ between Eq. (32) and (33), we obtain:

By eliminating $\stackrel{-}{\phi }$ between Eqs. (32) and (33), we get:

where $L=\frac{\left({\alpha }_2+{\alpha }_5+{\alpha }_1{\alpha }_6\right)}{\left(1+{\delta }^2{\alpha }_1{\alpha }_6\right)}$ and $M=\frac{{\alpha }_2{\alpha }_5}{\left(1+{\delta }^2{\alpha }_1{\alpha }_6\right)}$.

The bounded solutions at $r=0$ of the Eqs. (35) and (36) take the forms:

where $I_0\left(\mathrm{*}\right)$ is the modified Bessel function of the first kind of order zero, and $\pm k_1$, $\pm k_2$ are the roots of the characte, ristic equation:

For the thermal boundary condition, we consider the edge of the cylinder $r=a$ to be thermally loaded as follows:

where $g\left(t\right)$ is the function of the thermal loading and ${\phi }_o$ is constant (the thermal loading strength). For the mechanical boundary conditions, we consider the edge of the cylinder $r=a$ is connected to a rigid foundation which can prevent any displacement which leads to zero volumetric deformation as follows:

Applying Laplace transform on the Eqs. (40) and (41), we obtain:

Applying the boundary conditions in the Eqs. (37) and (38), we get the following system:

By solving the system in Eq. (43) and Eq. (44), we get:

Hence, we have:

To get the displacement function, we use the Eqs. (28) and (46) as follows:

which gives:

We use the well-known relation of Bessel integration as follows:

where $I_1\left(\mathrm{*}\right)$ is the modified Bessel function of the first kind of first order.

Hence, we obtain:

To obtain the dynamical temperature, we substitute from equations (45) and (46) in the Eqs. (34) to be in the form:

To get the stress distribution and to avoid the singularity when $r=0$, we take the average of the three principal stresses components as follows:

We re-write the Eq. (52) to be in the form:

where ${\alpha }_9=\left({\beta }^2-4/3\right)\left(1+{\tau }^{\alpha }{s}^{\alpha }\right)$.

Substitute from Eqs. (46) and (51) in the Eq. (53), hence, we get:

The conducting and dynamical temperature increments, pressure, displacement, and average stress can both be measured using Riemann-sum approximation techniques over time. This method is used to invert some function’s Laplace transformation [26]:

where “$i$” is an imaginary number unit, and “$Re$” is the real part. For convergence with a faster process, many numerical experiments have shown that the value $\kappa$ satisfies the relation $\kappa t\approx \text{4.7}$ [26].

3. Numerical results and discussion

Copper is known as the thermoelastic material for the numerical results and for the various physical constants we take the following values: $K=$386 kg m k^-1 s^-3, ${\alpha }_T=$1.78×10^-5 k^-1, $\rho =$8954 kg m^-3, $T_o=$ 293 k, $C_E=$383.1 m² k^-1s^-2, $\mu =$3.86 10¹⁰ kg m^-1 s^-2, $\lambda =$7.76×10¹⁰ kg m^-1 s^-2.

Thus, we get the non-dimensional values of the problem as [8, 24]: $b=$0.01047, ${\epsilon }_1=$ 0.0419, $\epsilon =$1.6086, ${\beta }^2=$ 4, ${\phi }_0=$ 1.0, ${\tau }_o=$ 0.02, $\tau =$ 0.01, $\tilde{c}=$ 0.1 (assumed).

The numerical results of the conductive and dynamical temperature increments, the strain, the displacement, and the average stress distributions have been figured for a wide range of the dimensionless radial distance $r\left(0\le r\le 2.0\right)$ at the instant value of dimensionless time $t=$ 1.0.

In Figs. 2-6, the calculations have been carried out for various values of the fractional-order parameter $\alpha =\left(\mathrm{0.0,0.5,0.9}\right)$in the context of the hyperbolic two-temperature thermoelasticity model to stand on the effect of this parameter on all the studied functions.

It is noted from Figs. 2 and 3 that the fractional-order parameter has very limited effects on the conductive and dynamical temperature increment. It is expectable results where the fractional-order definition has been applied to the strain function.

Fig. 2The conductive temperature distribution with the variance value of the fractional-order parameter

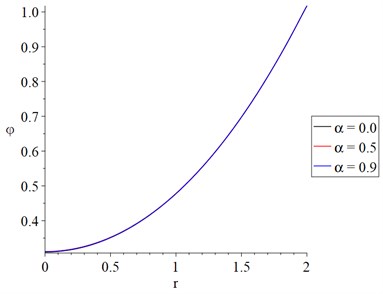
Fig. 3The dynamical temperature distribution with variance value of fractional order parameter

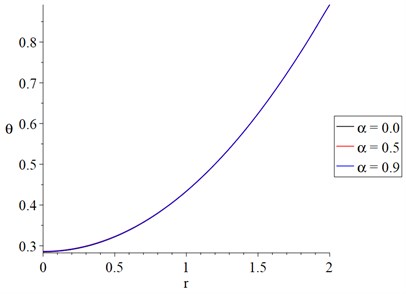
Fig. 4 shows that the fractional-order parameter has a significant effect on the strain distributions. The absolute values of the peak points of the strain distribution take the following order:

Fig. 5 shows that the fractional-order parameter has a significant effect on the displacement distributions, and this effect is visible near the impact of the thermal shock. The absolute values of the displacement at the edge of the cylinder $r=a$ take the following order:

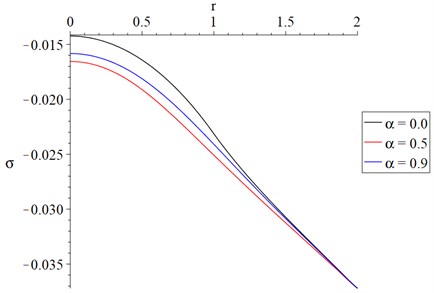
Fig. 6 shows that the fractional-order parameter has a significant effect on the average stress distributions. The absolute values of the average stress at the center of the cylinder $r=0$ take the following order:

Fig. 4The strain distribution with variance value of fractional order parameter

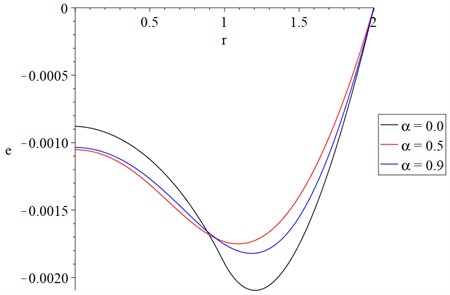
Fig. 5The displacement distribution with variance value of fractional order parameter

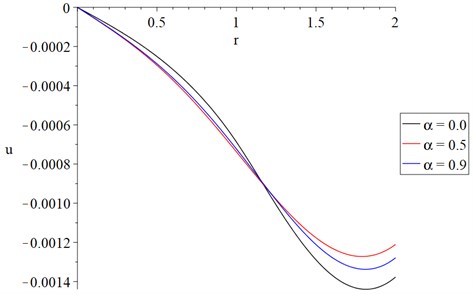
Fig. 6The average stresses distribution with variance value of fractional order parameter

In Figs. 7-11, the calculations have been carried out for various models of thermoelasticity (one-temperature, two-temperature, and hyperbolic two-temperature) without fractional-order strain $\alpha =\text{0.5}$ to stand on the two-temperature parameter effects on all the studied functions.

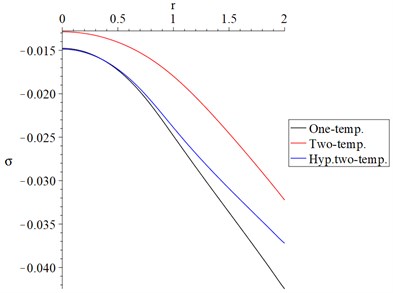
In Fig. 7, it is noticed that the behavior of the conductive temperature increment distributions in the context of the one-temperature and hyperbolic two-temperature models is closed but with different values. In contrast, the behavior of the classical two-temperature model is different. The curves of the one-temperature and hyperbolic two-temperature models fail down close to zero, more than the curve of the two-temperature model. The one-temperature and hyperbolic two-temperature models offer thermal waves with finite speed of propagation while the model of classical two-temperature parameter offers thermal waves with an infinite speed of propagation.

Fig. 8 shows that the dynamical temperature increment distributions in the context of the one-temperature and hyperbolic two-temperature models have the same behavior but with different values, while the behavior of the classical two-temperature model is different. The values of the dynamical temperature increment based on the one-temperature model in Fig. 8 coincide with the value of the conductive temperature increment in Fig. 7 based on the same model.

Fig. 7The conductive temperature increment distribution with variance models and α=0.5

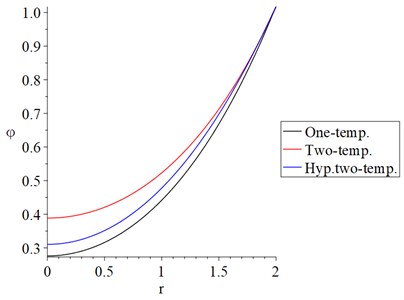
Fig. 8The dynamical temperature increment distribution with variance models α=0.5

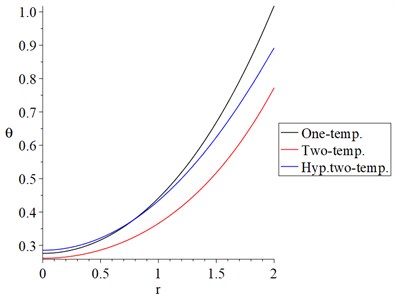
Fig. 9 shows that the strain distributions in the context of the one-temperature and hyperbolic two-temperature models have the same behavior but with different values, while its behavior based on the classical two-temperature model is different. The absolute values of the peak points of the strain take the following order:

Fig. 9The strain increment distribution with variance models α=0.5

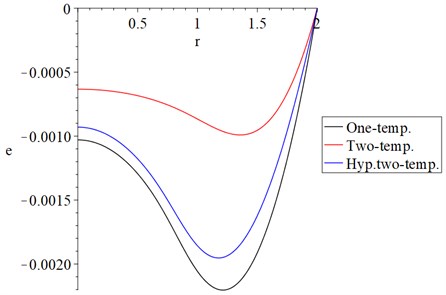
Fig. 10 shows that the displacement distributions in the context of the one-temperature and hyperbolic two-temperature models have closed behavior, while its behavior based on the classical two-temperature model is different. The values of the peak points of the displacement take the following order:

Fig. 11 shows that the average stress distributions in the context of the one-temperature and hyperbolic two-temperature models have a closed behavior, while its behavior based on the classical two-temperature model is different. The absolute values of the stress in the edge of the cylinder $r=a$ take the following order:

We can see that for the special cases of zero fractional order of strain, one-temperature model, and classical two-temperature model, the results agree with the results in the publications [8, 27, 28].

Fig. 10The displacement distribution with variance models α=0.5

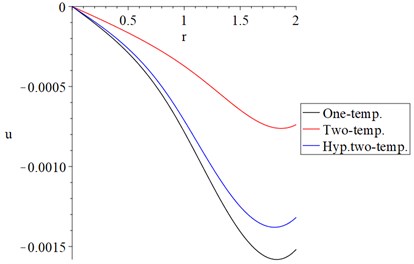
Fig. 11The average stresses distribution with variance models α=0.5

4. Conclusions

The issue of a thermoelastic homogeneous isotropic infinite cylindrical medium when the bounding surface is thermally shocked and no volume deformation is addressed in this article. One-temperature, classical two-temperature, and hyperbolic two-temperature models have also been used to solve the problem.

The fractional-order parameter has negligible impacts on conductive and dynamical temperature increments, but has a substantial influence on the strain, displacement, and average stresses, according to the numerical data.

The one-temperature model, like the hyperbolic two-temperature model, produces thermal waves with finite propagation speeds, while the classical two-temperature model generates thermal waves with an infinite propagation speed.

As a result, the hyperbolic two-temperature thermoelasticity model is a good fit for describing the thermodynamic behavior of thermoelastic materials.