Wave propagation in different theories of fractional thermoelasticity

Singh, Baljeet

doi:10.21595/jets.2023.23067

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 01 May 2023

Check for updates

Wave propagation in different theories of fractional thermoelasticity

Baljeet Singh¹

¹Department of Mathematics, Post Graduate Government College, Sector-11, Chandigarh, 160 011, India

Cite the article Download PDF

Downloads 201

Abstract

In the present paper, the theories of fractional thermoelasticity with derivative and integral fractional orders are employed to study the homogeneous plane waves and the Rayleigh surface waves. The governing equations of homogeneous and isotropic generalized fractional thermoelasticity are solved for plane wave solutions and a dispersive velocity equation is obtained. There exists one transverse and two coupled longitudinal waves in a two-dimensional model of fractional thermoelastic medium where the speeds of coupled longitudinal waves are found to be dependent on the derivative and integral fractional orders. The Rayleigh waves is also studied along the traction-free surface of a half-space of a generalized fractional thermoelastic solid. The governing equations are solved for the general surface wave solutions which follow the decaying conditions in the half-space. A Rayleigh wave secular equation is obtained for thermally insulated surface. For a particular example of the present model, the numerical values of the speeds of coupled longitudinal waves and the Rayleigh wave are computed and graphically illustrated to visualize the effects of derivative and integral fractional orders and the circular frequency on the wave speeds.

Highlights

Sherief and Youssef models of fractional thermoelasticity are applied to investigate the homogeneous plane waves and the Rayleigh surface wave.
Two coupled longitudinal waves and one transverse wave propagate in the plane of a fractional thermoelastic medium.
A dispersion equation of Rayleigh wave along a stress-free thermally insulated surface of a half-space of a fractional thermoelastic material is derived.
The thermal field, derivative fractional order and integral fractional order affect the speeds of both plane and Rayleigh surface waves.
The effects of fractional orders on the speeds both plane and Rayleigh surface waves are observed more considerable in higher frequency range.

1. Introduction

Biot [1] formulated the hyperbolic-parabolic field equations for coupled theory of thermoelasticity. The coupled theory of thermoelasticity was generalized by Lord and Shulman [2] and Green and Lindsay [3] by using the hyperbolic field equations. A detailed analysis and applications of these theories were presented by Ignaczak and Ostoja-Starzewski [4] and Hetnarski and Ignaczak [5].

In last few years, the fractional calculus was employed for improving various existing physical process models. The fractional order derivatives and integrals are found more useful and economical in solving certain physical problems as compared to the classical approach. Various materials like colloids, glassy, amorphous, porous, polymers, etc exist where fractional heat conduction models are appropriate instead of classical Fourier type heat conduction models as classical models break down in such materials. During the second half of 19th century, the fractional derivatives and integrals theories came into existence. Caputo and Mainardi [6, 7] and Caputo [8] made an important connection of fractional derivatives with the linear viscoelasticity theory and their outcomes were verified with the experimental results. Using the fractional heat conduction equation, Povstenko [9] formulated a quasi-static theory of uncoupled thermoelasticity. Making use of the heat conduction equation involving the Caputo time-fractional derivative, Povstenko [10] also analysed the thermal stresses in an infinite body containing a circular cylindrical hole. Sherief et al. [11] and Youssef [12] introduced alternative thermoelastic models using fractional calculus. Ezzat [13, 14] developed a novel fractional heat conduction equation by employing the Taylor series expansion of time-fractional order developed by Jumarie [15]. Using the fractional derivatives and integrals, El-Karamany and Ezzat [16] modified the Cattaneo heat equation [17] to formulate the two models of two-temperature fractional thermoelasticity. Thereafter, various theories of fractional thermoelasticity have been developed with additional parameters.

The propagation of waves has wide uses in different scientific areas including mineral and oil exploration, geophysical exploration and seismology. Particularly, the surface waves are more useful in the fields of geophysics, earthquake and geodynamics. Lord Rayleigh [18] was first to explore the existence of surface waves known as Rayleigh waves propagating on the free surface of an isotropic solid half-space. In contrast to the body waves, the Rayleigh waves have slower energy attenuation and due to this reason these cause destruction to the structure. These surface waves can propagate along the thick solid surface with one wave length penetration and behave differently for surface defects. These waves are mainly applied for characterization of material and to investigate the structural and mechanical properties of the objects. In context of thermoelastic theories, the propagation of Rayleigh wave finds numerous uses in different engineering fields and future technologies. The surface waves in context of thermoelastic theories were analyzed by different investigators. Few prominent research works are highlighted. For example, the thermal effects on the Rayleigh wave speed were noticed by Lockett [19]. The Rayleigh wave in a prestressed thermoelastic medium was considered by Flavin [20]. The Rayleigh wave along both isothermal and insulated surfaces was examined by Chadwick and Windle [21]. Thereafter, various problems on the Rayleigh waves in thermoelasticity with additional parameters were studied [22-33]. The present work is motivated by the theoreis of fractional thermoelasticity given by Sherief et al. [11] and Youssef [12]. In this paper, the propagation of the homogeneous plane waves and the Rayleigh waves in an isotropic generalized fractional thermoelastic medium is explored. To observe the effects of circular frequency and fractional orders, the speeds of coupled longitudinal waves and Rayleigh surface wave are graphically illustrated.

2. Governing equations

Following Lord and Shulman [2], Sherief [11] and Youssef [12], the governing equations of linear, homogenous and isotropic fractional thermoelasticity without body forces and heat sources, are.

(a) Constitutive equations:

1

e_{i j} = \frac{1}{2} (u_{i, j} + u_{j, i}),

2

σ_{i j} = 2 μ e_{i j} + (λ e_{k k} - γ T) δ_{i j} .

(b) Equations of motion:

3

μ u_{i, j j} + (λ + μ) u_{j, i j} - γ T_{, i} = ρ {\ddot{u}}_{i} .

(c) Heat Equations.

(i) Sherief model:

4

K T_{, i i} = (\frac{\partial}{\partial t} + τ_{0} \frac{\partial^{α + 1}}{\partial t^{α + 1}}) (ρ c_{E} T + γ T_{0} e_{i i}),

where $α$ is a constant such that $0 < α \leq 1$ . In the limiting case $α \to 1$ , the Eq. (4) reduces to the heat conduction equation obtained by Lord and Shulman [3] with single relaxation time. In the limiting case $α \to 0$ , the Eq. (4) reduces to the heat conduction equation for the coupled theory of thermoelasticity when $τ_{0} = 0$ .

(ii) Youssef model:

5

K I^{ν - 1} T_{, i i} = (\frac{\partial}{\partial t} + τ_{0} \frac{\partial^{2}}{\partial t^{2}}) (ρ c_{E} T + γ T_{0} e_{i i}), 0 < ν \leq 2,

where $I^{(ν)}$ is Riemann-Liouville fractional integral operator given by:

I^{(ν)} g (t) = \frac{1}{Γ (ν)} \int_{0}^{t} ‍ (t - τ)^{ν - 1} g (τ) d τ, 0 < ν \leq 2, I^{0} g (t) = g (t),

and $0 < ν < 1$ for weak conductivity, $ν = 1$ for normal conductivity and $1 < ν \leq 2$ for strong conductivity. $σ_{i j}$ are the stress tensor components, $e_{i j}$ are the strain tensor components, $u_{i}$ are the displacement components, $δ_{i j}$ is the Kronecker delta, $λ$ , $μ$ are Lame’s constants, $ρ$ is the density of the medium, $T$ is change in temperature with reference temperature $T_{0}$ , $K$ is the thermal conductivity, $c_{E}$ is the specific heat at constant strain, $τ_{0}$ is a non-negative parameter called as the relaxation time, $γ = (3 λ + 2 μ) α_{0}$ and $α_{0}$ is the thermal expansion coefficient. The overlayed dot symbolizes the time partial differentiation. The subscripts given after a comma symbolizes space partial differentiation.

A thermally conducting isotropic and homogeneous elastic material is considered at reference temperature $T_{0}$ in the unstrained state. A Cartesian system of axes is considered with the origin at plane surface $y = 0$ of the half-space $y \geq 0$ . The positive $y$ -axis is taken normal into the half-space. The surface $y = 0$ is assumed as stress free and without any heat transfer across the surface. The propagation direction of elastic waves is selected along the $x$ -axis with equal displacement of particles on a line parallel to $z$ -axis. Then, all the field quantities will not dependent on $z$ -coordinates. Using the Helmholtz’s decomposition given below:

6

u_{1} = ϕ_{, 1} + ψ_{, 2}, u_{2} = ϕ_{, 2} - ψ_{, 1},

the governing Eqs. (3) and (4) are specialized in $x$ - $y$ plane as under:

7

μ (ψ_{, 11} + ψ_{, 22}) = ρ \ddot{ψ},

8

(λ + 2 μ) (ϕ_{, 11} + ϕ_{, 22}) - γ T = ρ \ddot{ϕ} .

(i) Sherief model:

9

K (T_{, 11} + T_{, 22}) = (\frac{\partial}{\partial t} + τ_{0} \frac{\partial^{α + 1}}{\partial t^{α + 1}}) [ρ c_{E} T + γ T_{0} (ϕ_{, 11} + ϕ_{, 22})] .

(ii) Youssef model:

10

K I^{ν - 1} (T_{, 11} + T_{, 22}) = (\frac{\partial}{\partial t} + τ_{0} \frac{\partial^{2}}{\partial t^{2}}) [ρ c_{E} T + γ T_{0} (ϕ_{, 11} + ϕ_{, 22})] .

3. Plane waves

The following type of plane wave solutions of Eqs. (7) to (10) are sought:

11

{ψ, ϕ, T} = {A, B, C} e^{ι k (x s i n θ + y c o s θ) - ι ω t},

where $θ$ is the propagation angle, $k$ is the complex wavenumber and $ω$ is the circular frequency.

Using Eq. (11) into Eqs. (7) to (10), the following equation in velocity is derived:

12

(V^{2} - c_{2}^{2}) [V^{4} - (K^{*} + ϵ^{*} + c_{1}^{2}) V^{2} + K^{*} c_{1}^{2}] = 0,

where:

13

V^{2} = \frac{ω^{2}}{k^{2}}, ϵ^{*} = \frac{γ^{2} T_{0}}{ρ^{2} c_{E}}, c_{1}^{2} = \frac{λ + 2 μ}{ρ}, c_{2}^{2} = \frac{μ}{ρ},

and (a) for Sherief model:

14

K^{*} = \frac{K}{ρ c_{E} τ_{1}}, τ_{1} = τ_{0} (- i ω)^{α - 1} + \frac{i}{ω} .

(a) for Youssef model:

15

K^{*} = \frac{K}{ρ c_{E} τ_{2}} {(\frac{i}{ω})}^{ν - 1}, τ_{2} = τ_{0} + \frac{i}{ω} .

The Eq. (12) has following three roots:

16

V_{1}^{2} = \frac{1}{2} [(K^{*} + ϵ^{*} + c_{1}^{2}) + \sqrt{(K^{*} + ϵ^{*} + c_{1}^{2})^{2} - 4 K^{*} c_{1}^{2}}],

17

V_{2}^{2} = \frac{1}{2} [(K^{*} + ϵ^{*} + c_{1}^{2}) - \sqrt{(K^{*} + ϵ^{*} + c_{1}^{2})^{2} - 4 K^{*} c_{1}^{2}}],

18

V_{3}^{2} = c_{2}^{2},

which shows that there exists two coupled longitudinal waves with distinct speeds $v_{1} = R e (V_{1})$ and $v_{2} = R e (V_{2})$ and one transverse wave with speed $v_{3} = V_{3}$ in an isotropic and homogeneous fractional thermoelastic medium [34]. Here, the phase speeds $v_{1}$ and $v_{2}$ of the coupled longitudinal waves are dependent on the derivative fractional order in Sherief model or integral fractional order in Youssef model, respectively.

4. Rayleigh surface wave

The Rayleigh wave propagation is considered in the $x$ -direction and decaying in the $y$ -direction with wave number $k (> 0)$ and velocity $v (> 0)$ . The appropriate displacement and temperature potential functions for propagation of Rayleigh waves along the surface $y = 0$ , are selected as:

19

ϕ (x, y, t) = B_{1} e^{- η k y} e^{i k (x - v t)},

T (x, y, t) = B_{2} e^{- η k y} e^{i k (x - v t)},

ψ (x, y, t) = B_{3} e^{- η k y} e^{i k (x - v t)},

where $η$ is a complex coefficient with $I m (η) > 0$ to satisfy the decay conditions in the half-space $y > 0$ . The unknowns $B_{1}$ , $B_{2}$ and $B_{3}$ are the polarization vectors.

Making use of Eq. (19) in Eqs. (7) to (10), the appropriate solutions in half-space $y > 0$ for surface wave are obtained as:

20

ϕ (x, y, t) = \sum_{j = 1}^{2} ‍ B_{1 j} e^{- η_{j} k y} e^{i k (x - v t)},

T (x, y, t) = \sum_{j = 1}^{2} ‍ r_{j} B_{1 j} e^{- η_{j} k y} e^{i k (x - v t)},

ψ (x, z, t) = B_{3} e^{- η_{3} k y} e^{i k (x - v t)},

where the unknowns $B_{1 j}$ and $B_{3}$ are amplitudes of displacement potentials and temperature and (a) for Sherief case:

21

η_{1}^{2} + η_{2}^{2} = (1 - \frac{ρ v^{2}}{λ + 2 μ}) + (1 - \frac{1}{K_{1}^{*}}) - \frac{ϵ^{*}}{K_{1}^{*}},

η_{1}^{2} η_{2}^{2} = (1 - \frac{ρ v^{2}}{λ + 2 μ}) (1 - \frac{1}{K_{1}^{*}}) - \frac{ϵ^{*}}{K_{1}^{*}},

η_{3}^{2} = (1 - \frac{ρ v^{2}}{μ}),

22

r_{j} = \frac{k^{2} (λ + 2 μ) (a_{1} + η_{j}^{2})}{γ} = \frac{k^{2} γ T_{0} (1 - η_{j}^{2})}{ρ c_{E} (a_{2} + K_{1}^{*} η_{j}^{2})}, (j = 1,2),

and (b) for Youssef case:

23

η_{1}^{2} + η_{2}^{2} = (1 - \frac{ρ v^{2}}{λ + 2 μ}) + (1 - \frac{v^{2}}{K_{2}^{*}}) - \frac{ϵ^{*} v^{2}}{K_{2}^{*}},

η_{1}^{2} η_{2}^{2} = (1 - \frac{ρ v^{2}}{λ + 2 μ}) (1 - \frac{v^{2}}{K_{2}^{*}}) - \frac{ϵ^{*} v^{2}}{K_{2}^{*}},

η_{3}^{2} = (1 - \frac{ρ v^{2}}{μ}),

24

r_{j} = \frac{k^{2} (λ + 2 μ) (a_{1} + η_{j}^{2})}{γ} = \frac{γ T_{0} (1 - η_{j}^{2}) ω^{2}}{ρ c_{E} (a_{3} + K_{2}^{*} η_{j}^{2})}, (j = 1,2),

where:

25

a_{1} = \frac{ρ v^{2}}{λ + 2 μ} - 1, a_{2} = 1 - K_{1}^{*}, a_{3} = v^{2} - K_{2}^{*},

26

K_{1}^{*} = \frac{K ω^{2}}{ρ c_{E} τ_{3} v^{2}}, K_{2}^{*} = \frac{K}{ρ c_{E} τ_{2}} {(\frac{i}{ω})}^{ν - 1}, τ_{3} = ι ω [1 + τ_{0} (- ι ω)^{α}] .

The required boundary conditions at thermally insulated stress-free surface $y = 0$ are vanishing of the tangential stress component, normal stress component and the normal heat flux component at $y = 0$ , i.e.:

27

σ_{12} = 0, σ_{22} = 0, \frac{\partial T}{\partial y} = 0,

where:

28

σ_{12} = μ (ψ_{, 11} - ψ_{, 22} + 2 ϕ_{, 12}),

σ_{22} = λ (ϕ_{, 11} + ϕ_{, 22}) + 2 μ (ϕ_{, 22} + ψ_{, 12}) - γ T .

The appropriate potential functions given by Eq. (20) satisfy the conditions Eq. (27) and a homogeneous system of three equations in $B_{11}$ , $B_{12}$ and $B_{3}$ are obtained after using first equations of Eq. (22) and Eq. (24). The non-trivial solution of the homogeneous system require the vanishing of the determinant of the coefficients matrix, i.e.:

29

{(\frac{ρ v^{2}}{μ} - 2)}^{2} [1 - \frac{ρ v^{2}}{λ + 2 μ} - η_{1}^{2} - η_{2}^{2} - η_{1} η_{2}] + 4 η_{1} η_{2} η_{3} (η_{1} + η_{2}) = 0 .

The Eq. (29) is dispersion equation of Rayleigh waves along the stress-free thermally insulated surface of an isotropic and homogeneous fractional thermoelastic solid half-space. In absence of thermal effects, the Eq. (29) reduces to:

30

(\frac{ρ v^{2}}{μ} - 2) (1 + η_{3}^{2}) + 4 η_{1}^{*} η_{3} = 0,

where:

31

η_{1}^{*} = \sqrt{1 - \frac{ρ v^{2}}{λ + 2 μ}} .

The Eq. (30) is the secular equation of the Rayleigh wave along the free surface of an isotropic elastic solid half-space as obtained by Lord Rayleigh [18].

5. Numerical results and discussion

For numerical illustrations of the speeds of homogeneous plane waves and the Rayleigh surface wave, the following relevant parameters of copper material at $T_{0} =$ 300 K are taken $ρ$ = 2.7×10³ Kg.m^-3, $λ =$ 5.775×10¹⁰ N.m^-2, $μ =$ 2.646×10¹⁰ N.m^-2, $K$ = 0.00492×10² W.m^-1.deg^-1, $c_{E}$ = 2.36×10² J.Kg^-1.deg^-1, $τ_{0}$ = 0.005 s.

The velocity Eq. (12) is solved numerically to illustrate the effects of derivative fractional order $α$ , integral fractional order $ν$ and circular frequency $ω$ on the speeds $v_{1}$ and $v_{2}$ of the coupled longitudinal waves. As shown in Fig. 1(a) and 1(b), a significant effect of fractional order parameter $α$ on wave speeds of coupled longitudinal waves is observed in higher frequency range.

Fig. 1The speed variations of coupled longitudinal waves against the derivative fractional order α for distinct values of ω

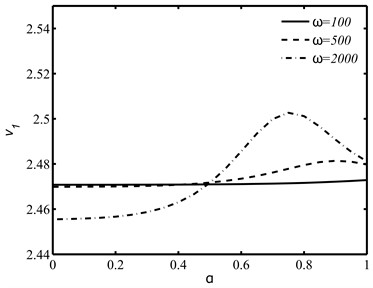
$The speed variations of coupled longitudinal waves against the derivative fractional order α for distinct values of ω$

a)

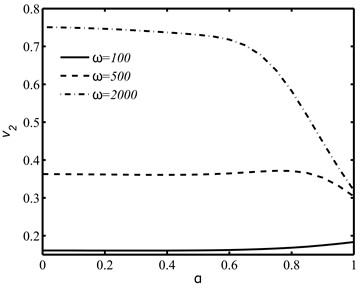
$The speed variations of coupled longitudinal waves against the derivative fractional order α for distinct values of ω$

b)

The speed variations in Figs. 2(a) and 2(b) show that the speeds $v_{1}$ or $v_{2}$ of the coupled longitudinal waves increases or decreases sharply in weak conductivity region $(0 < ν < 1)$ and the effect of circular frequency $ω$ on wave speeds is more prominent in weak conductivity region as compared to the strong conductivity region $(1 < ν < 2)$ .

With the use of functional iteration method, the dispersion Eq. (29) is numerically solved for the dimensionless speed $v_{R} = R e \{\sqrt{ρ v^{2} / μ}\}$ of the Rayleigh wave. The impacts of derivative fractional order $α$ , integral fractional order $ν$ and the circular frequency on the wave speed $v_{R}$ of the Rayleigh wave are illustrated in Figs. 3 and 4. It is observed that the effects of fractional orders $α$ and $ν$ on the speed are found more prominent in higher frequency range.

Fig. 2The speed variations of coupled longitudinal waves against the integral fractional order ν for distinct values of ω

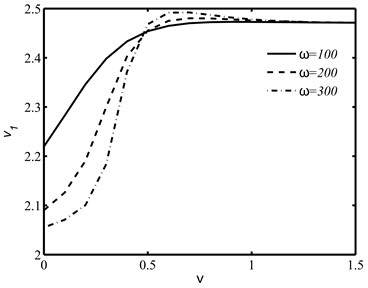
$The speed variations of coupled longitudinal waves against the integral fractional order ν for distinct values of ω$

a)

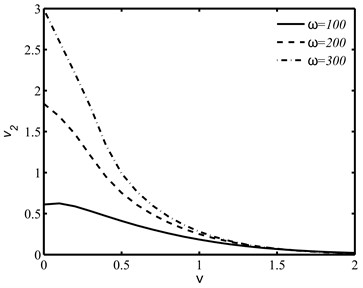
$The speed variations of coupled longitudinal waves against the integral fractional order ν for distinct values of ω$

b)

Fig. 3The influences of derivative fractional parameter α and the circular frequency ω on the normalized Rayleigh wave speed vR

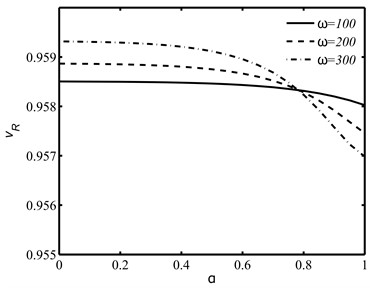
$The influences of derivative fractional parameter α and the circular frequency ω on the normalized Rayleigh wave speed vR$

a)

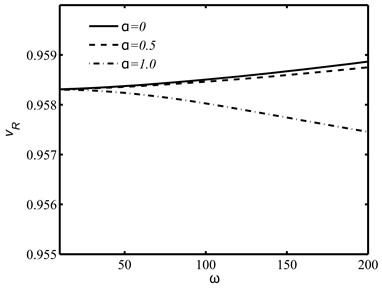
$The influences of derivative fractional parameter α and the circular frequency ω on the normalized Rayleigh wave speed vR$

b)

Fig. 4The influences of integral fractional parameter ν and the circular frequency ω on the normalized Rayleigh wave speed vR

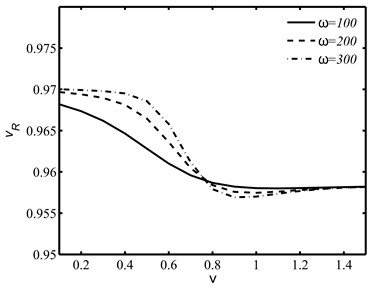
$The influences of integral fractional parameter ν and the circular frequency ω on the normalized Rayleigh wave speed vR$

a)

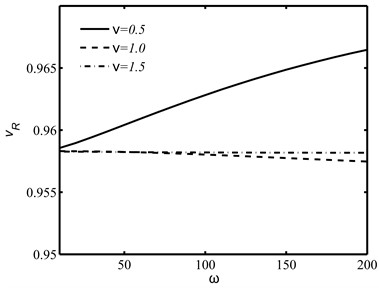
$The influences of integral fractional parameter ν and the circular frequency ω on the normalized Rayleigh wave speed vR$

b)

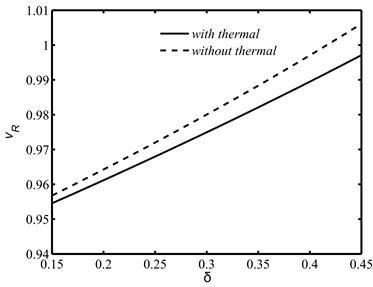
The speed $v_{R}$ of the Rayleigh wave as shown in Fig. 5 increases linearly with the non-dimensional elastic parameter $δ = μ / (λ + 2 μ)$ and the effects of fractional orders $α$ and $ν$ are found more prominent at larger values of $δ$ . The thermal effect on the wave speed $v_{R}$ against $δ$ is also illustrated in Fig. 6 where in absence of thermal disturbances, the speed enhances at each $δ$ .

Fig. 5The Rayleigh wave speed against the non-dimensional material parameter δ for different values of derivative fractional parameter α and integral fractional parameter ν

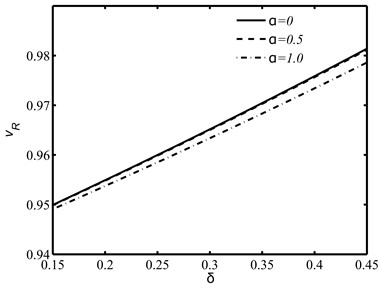
$The Rayleigh wave speed against the non-dimensional material parameter δ for different values of derivative fractional parameter α and integral fractional parameter ν$

a)

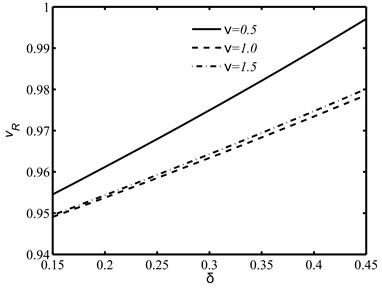
$The Rayleigh wave speed against the non-dimensional material parameter δ for different values of derivative fractional parameter α and integral fractional parameter ν$

b)

Fig. 6Thermal effects on the Rayleigh wave speed against the non-dimensional material parameter δ

6. Conclusions

Sherief and Youssef models of fractional thermoelasticity are applied to study the homogeneous plane waves and the Rayleigh surface wave in a generalized fractional thermoelastic medium. It is found that there exists two coupled longitudinal waves and one transverse wave in a plane of a fractional thermoelastic medium. In both Sherief and Youssef models, the coupled longitudinal waves are found affected by thermal fields and fractional order parameters. A dispersion equation of Rayleigh wave along a stress-free thermally insulated surface of a halfspace of a fractional thermoelastic material. The numerical computations and illustrations of wave speeds of plane and Rayleigh wave based on a particular material show that the thermal field, derivative fractional order and integral fractional order changes significantly the speeds of both plane and surface waves. The effects of fractional orders are observed more significant in high frequency range. The present theoretical predictions on plane and surface waves in both Sherief and Youssef models of fractional thermoelasticity may be applied in possible experimental studies on the heat conduction in materials like colloids, glassy, amorphous, porous, polymers, etc.

References

M. A. Biot, “Thermoelasticity and irreversible thermodynamics,” Journal of Applied Physics, Vol. 27, No. 3, pp. 240–253, Mar. 1956, https://doi.org/10.1063/1.1722351

Publisher
A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, pp. 1–7, Mar. 1972, https://doi.org/10.1007/bf00045689

Publisher
H. W. Lord and Y. Shulman, “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, pp. 299–309, Sep. 1967, https://doi.org/10.1016/0022-5096(67)90024-5

Publisher
J. Ignaczak and M. Ostoja-Starzewski, Thermoelasticity with Finite Wave Speeds. Oxford University Press, 2009, https://doi.org/10.1093/acprof:oso/9780199541645.001.0001

Publisher
Richard B. Hetnarski and Jozef Ignacza, “Generalized thermoelasticity,” Journal of Thermal Stresses, Vol. 22, No. 4-5, pp. 451–476, Jun. 1999, https://doi.org/10.1080/014957399280832

Publisher
M. Caputo and F. Mainardi, “A new dissipation model based on memory mechanism,” Pure and Applied Geophysics PAGEOPH, Vol. 91, No. 1, pp. 134–147, 1971, https://doi.org/10.1007/bf00879562

Publisher
M. Caputo and F. Mainardi, “Linear models of dissipation in anelastic solids,” La Rivista del Nuovo Cimento, Vol. 1, No. 2, pp. 161–198, Apr. 1971, https://doi.org/10.1007/bf02820620

Publisher
M. Caputo, “Vibrations of an infinite viscoelastic layer with a dissipative memory,” The Journal of the Acoustical Society of America, Vol. 56, No. 3, pp. 897–904, Sep. 1974, https://doi.org/10.1121/1.1903344

Publisher
Y. Z. Povstenko, “Fractional heat conduction equation and associated thermal stress,” Journal of Thermal Stresses, Vol. 28, No. 1, pp. 83–102, Dec. 2004, https://doi.org/10.1080/014957390523741

Publisher
Y. Z. Povstenko, “Fractional radial heat conduction in an infinite medium with a cylindrical cavity and associated thermal stresses,” Mechanics Research Communications, Vol. 37, No. 4, pp. 436–440, Jun. 2010, https://doi.org/10.1016/j.mechrescom.2010.04.006

Publisher
H. H. Sherief, A. M. A. El-Sayed, and A. M. Abd El-Latief, “Fractional order theory of thermoelasticity,” International Journal of Solids and Structures, Vol. 47, No. 2, pp. 269–275, Jan. 2010, https://doi.org/10.1016/j.ijsolstr.2009.09.034

Publisher
H. M. Youssef, “Theory of fractional order generalized thermoelasticity,” Journal of Heat Transfer, Vol. 132, No. 6, pp. 1–7, Jun. 2010, https://doi.org/10.1115/1.4000705

Publisher
M. A. Ezzat, “Thermoelectric MHD non-Newtonian fluid with fractional derivative heat transfer,” Physica B: Condensed Matter, Vol. 405, No. 19, pp. 4188–4194, Oct. 2010, https://doi.org/10.1016/j.physb.2010.07.009

Publisher
M. A. Ezzat, “Magneto-thermoelasticity with thermoelectric properties and fractional derivative heat transfer,” Physica B: Condensed Matter, Vol. 406, No. 1, pp. 30–35, Jan. 2011, https://doi.org/10.1016/j.physb.2010.10.005

Publisher
G. Jumarie, “Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio,” Computers and Mathematics with Applications, Vol. 59, No. 3, pp. 1142–1164, Feb. 2010, https://doi.org/10.1016/j.camwa.2009.05.015

Publisher
A. S. El-Karamany and M. A. Ezzat, “Convolutional variational principle, reciprocal and uniqueness theorems in linear fractional two-temperature thermoelasticity,” Journal of Thermal Stresses, Vol. 34, No. 3, pp. 264–284, Feb. 2011, https://doi.org/10.1080/01495739.2010.545741

Publisher
C. R. Cattaneo, “Sur une de le’quation de la chaleur e’liminant le Paradoxe dune propagation instantane’e,” Comptes Rendus de 1’Academie des Sci-ences de Paris, Vol. 247, pp. 431–433, 1958.

Search CrossRef
L. Rayleigh, “On waves propagated along the plane surface of an elastic solid,” Proceedings of the London Mathematical Society, Vol. 17, No. 1, pp. 4–11, 1885, https://doi.org/10.1112/plms/s1-17.1.4

Publisher
F. J. Lockett, “Effect of thermal properties of a solid on the velocity of Rayleigh waves,” Journal of the Mechanics and Physics of Solids, Vol. 7, No. 1, pp. 71–75, Nov. 1958, https://doi.org/10.1016/0022-5096(58)90040-1

Publisher
J. N. Flavin, “Thermo-elastic Rayleigh waves in a prestressed medium,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 58, No. 3, pp. 532–538, Jul. 1962, https://doi.org/10.1017/s0305004100036811

Publisher
P. Chadwick and D. W. Windle, “Propagation of Rayleigh waves along isothermal and insulated boundaries,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, Vol. 280, No. 1380, pp. 47–71, Jul. 1964, https://doi.org/10.1098/rspa.1964.0130

Publisher
T. P. Ivanov, “On the propagation of thermoelastic Rayleigh waves,” Wave Motion, Vol. 10, No. 1, pp. 73–82, Jan. 1988, https://doi.org/10.1016/0165-2125(88)90007-8

Publisher
A. M. Abd-Alla and S. M. Ahmed, “Rayleigh waves in an orthotropic thermoelastic medium under gravity field and initial stress,” Earth, Moon, and Planets, Vol. 75, No. 3, pp. 185–197, Oct. 1996, https://doi.org/10.1007/bf02592996

Publisher
A. E. Abouelregal, “Rayleigh waves in a thermoelastic solid half space using dual-phase-lag model,” International Journal of Engineering Science, Vol. 49, No. 8, pp. 781–791, Aug. 2011, https://doi.org/10.1016/j.ijengsci.2011.03.007

Publisher
S. Chiriţă, “On the Rayleigh surface waves on an anisotropic homogeneous thermoelastic half space,” Acta Mechanica, Vol. 224, No. 3, pp. 657–674, Mar. 2013, https://doi.org/10.1007/s00707-012-0776-z

Publisher
A. V. Bucur, F. Passarella, and V. Tibullo, “Rayleigh surface waves in the theory of thermoelastic materials with voids,” Meccanica, Vol. 49, No. 9, pp. 2069–2078, Sep. 2014, https://doi.org/10.1007/s11012-013-9850-4

Publisher
R. Kumar and V. Gupta, “Rayleigh waves in generalized thermoelastic medium with mass diffusion,” Canadian Journal of Physics, Vol. 93, No. 10, pp. 1039–1049, Oct. 2015, https://doi.org/10.1139/cjp-2014-0681

Publisher
B. Singh, “Rayleigh wave in a thermoelastic solid half-space with impedance boundary conditions,” Meccanica, Vol. 51, No. 5, pp. 1135–1139, May 2016, https://doi.org/10.1007/s11012-015-0269-y

Publisher
F. Passarella, V. Tibullo, and G. Viccione, “Rayleigh waves in isotropic strongly elliptic thermoelastic materials with microtemperatures,” Meccanica, Vol. 52, No. 13, pp. 3033–3041, Oct. 2017, https://doi.org/10.1007/s11012-016-0591-z

Publisher
S. Biswas, “Stroh analysis of Rayleigh waves in anisotropic thermoelastic medium,” Journal of Thermal Stresses, Vol. 41, No. 5, pp. 627–644, May 2018, https://doi.org/10.1080/01495739.2018.1425940

Publisher
B. Singh and S. Verma, “On propagation of Rayleigh type surface wave in five different theories of thermoelasticity,” International Journal of Applied Mechanics and Engineering, Vol. 24, No. 3, pp. 661–673, Sep. 2019, https://doi.org/10.2478/ijame-2019-0041

Publisher
B. Singh, “Rayleigh-type surface waves in a nonlocal thermoelastic solid half space with voids,” Waves in Random and Complex Media, Vol. 31, No. 6, pp. 2103–2114, Nov. 2021, https://doi.org/10.1080/17455030.2020.1721612

Publisher
M. D. Sharma, “Thermoelastic Rayleigh wave: explicit expression for complex velocity,” Journal of Thermal Stresses, Vol. 44, No. 5, pp. 610–618, May 2021, https://doi.org/10.1080/01495739.2020.1860729

Publisher
H. Deresiewicz, “Plane waves in a thermoelastic solid,” The Journal of the Acoustical Society of America, Vol. 29, No. 2, pp. 204–209, Feb. 1957, https://doi.org/10.1121/1.1908832

Publisher

About this article

Received

22 November 2022

Accepted

03 January 2023

Published

01 May 2023

DOI

https://doi.org/10.21595/jets.2023.23067

Keywords

plane waves

Rayleigh wave

fractional thermoelasticity

secular equation

wave speed

derivative and integral fractional orders

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2021 11 11

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir, Adiya Dar, Mohamed I. A. Othman

Research article

2021 09 13

Hyperbolic two-temperature generalized thermoelasticity with fractional order strain of solid cylinder

Alaa A. El-Bary

Research article

2019 08 15

Ground vibration propagation and attenuation of vibrating compaction

Aijun Chen, Feng Cheng, Di Wu, Xianyuan Tang

Research article

2017 06 30

Analysis of blasting vibration wave propagation based on finite element numerical calculation and experimental investigations

Tung-Cheng Wang, Chin-Yu Lee, Iau-Teh Wang

B. Singh, “Wave propagation in different theories of fractional thermoelasticity,” Journal of Engineering and Thermal Sciences, Vol. 3, No. 1, pp. 1–10, May 2023, https://doi.org/10.21595/jets.2023.23067

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2023.23067
UR  - https://doi.org/10.21595/jets.2023.23067
TI  - Wave propagation in different theories of fractional thermoelasticity
T2  - Journal of Engineering and Thermal Sciences
AU  - Singh, Baljeet
PY  - 2023
DA  - 2023/05/01
PB  - JVE International Ltd.
SP  - 1-10
VL  - 3
IS  - 1
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Singh_2023,
	doi = {10.21595/jets.2023.23067},
	url = {https://doi.org/10.21595/jets.2023.23067},
	year = 2023,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {3},
	number = {1},
	pages = {1--10},
	author = {Baljeet Singh},
	title = {Wave propagation in different theories of fractional thermoelasticity},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]B. Singh, “Wave propagation in different theories of fractional thermoelasticity,” Journal of Engineering and Thermal Sciences, vol. 3, no. 1, pp. 1–10, May 2023, doi: 10.21595/jets.2023.23067.

Copy IEEE

Copied to clipboard!

Singh, Baljeet. “Wave Propagation in Different Theories of Fractional Thermoelasticity.” Journal of Engineering and Thermal Sciences 3, no. 1 (May 1, 2023): 1–10. https://doi.org/10.21595/jets.2023.23067.

Copy Chicago

Copied to clipboard!

Wave propagation in different theories of fractional thermoelasticity

Abstract

Highlights

1. Introduction

2. Governing equations

3. Plane waves

4. Rayleigh surface wave

5. Numerical results and discussion

6. Conclusions

References

About this article

Related Articles