Thermal shock problem of a generalized thermoelastic solid sphere affected by mechanical damage and thermal diffusion

1. Introduction

One of the key problems of thermodynamics is simulating thermoelasticity. Authors and researchers obtained such mathematical model systems for the dissemination of science and heat in thermomechanical wave solids. While experimental research at a constant rate of propagation of mechanical and thermal waves is one measure of consistency in a model of success, all these simulations are not stable or compatible with material behaviors, as experimental research with a constant rate of propagations on mechanical and thermal waves is a measure of consistency in a model of success. Thermomechanical mechanisms of transformation cannot be limited by an elastic matter to a single work. The Lord and Shulman are the two most common formats. In this case, the conventional Fourier heat driving model was revised based on the second phenomenon and a non-Fourier theory that focused on one period of relaxation [1]. General thermoelasticity was formulated for the specific case of an isotropic body, and Lord and Shulman developed the concept of special thermoelasticity with a relaxation time scale [1]. This theory was extended by Sherief and Dhaliwal [2]. Previously, Biot's model has offered unlimited speed to the thermal waves as well as classical heat-conduction law modifications, which explains heat conductivity using the Fourier's law of heat conduction formula [3]. Youssef solved numerous thermoelastic phenomena for Lord-Shulman and his associates, particularly in the sense of spherical media [4-7].

Diffusion can be defined as the random moving of a group of particles from higher concentration regions to lower concentration regions. The concentration can be calculated using Fick's law [8-11]. Sherief et al. derived the governing equations for generalized thermo-diffusion in thermoelastic solids. They obtained a variational theorem for the governing equations and proved the uniqueness of these equations solutions under suitable conditions [8]. Sherief and Heba solve the first problem based on the generalized thermoelastic diffusion theory [9]. Aouadi solved a problem for an infinite elastic body contains a spherical cavity using the generalized thermoelastic diffusion model [10]. Hussein solved the problem of the spherical region in the context of the theory of generalized thermoelastic diffusion in a two-dimensions [12]. Sharma et al. studied the free vibration analysis of a nonlocal thermoelastic hollow cylinder with diffusion [13]. El-Karamany and Ezzat solved a problem of thermoelastic diffusion with memory-dependent derivatives [14]. Abbas and Marin applied the generalized thermoelastic theory with mass diffusion to a two-dimensional problem for a half-space [15]. El-Naggar et al. studied the effect of the magnetic field, rotation, thermal field, and the initial stress and also voids on the reflection of P-wave with one relaxation time. The formulation is applied to generalization, the Lord-Shulman theory with one relaxation time [16]. Marin et al. extended the domain of the influence theorem to cover the generalized thermoelasticity of anisotropic bodies with voids in the context of Lord-Shulman and Green-Lindsay theories [17].

The damage amount could be obtained by the area fraction [18]:

where the undamaged material is given by $D=\text{0}$, while the totally damaged material (fracture) is given by $D=\text{1}$. The nature values of the mechanical damage for any materials are $D=$ 0.2...0.5. In the isotropic damage case, the actual stresses components are given by [18]:

where ${\widehat{\sigma }}_{ij}$ are the stress components for the undamaged material.

A lot of work has been done under this concept of mechanical damage [19-28].

Almost all authors who considered spherical medium in their applications assumed that the body with a spherical cavity avoids the problem of singularity in the center of the sphere. Thibault et al. used the theory of L’Hospital to address the case of singularity in the thermoelastic rigid sphere as in [29].

This paper aims to introduce a mathematical model of a thermoelastic, unified, and isotropic solid sphere subjected to thermal diffusion. A diffusive substance’s thermal and chemical potential shocks will be loaded into the sphere's bounding structure. The governing equations will be developed as part of a generalized thermoelastic diffusion theory that included mechanical disruption.

2. Materials and methods

The control equations of a standard isotropic thermoelastic material with general thermal diffusion based on the model of Lord-Shulman, and the mechanical damage variable without the body forces and heat sources are determined by the application of the Sherief et al. model [1, 8-10, 30].

The equation of motion:

where ${\sigma }_{ij}$are the components of the stress tensor, $\rho$is the density, and $u_i$ are the displacement components.

The heat conduction equations:

where $K$ is the thermal conductivity, $T$ is the absolute temperature, $T_o$ is the reference temperature, $e_{ij}$ are the strain components, $t$is the time, $c_E$is the specific heat at constant strain, ${\beta }_1=\left(3\lambda +2\mu \right){\alpha }_T$, ${\alpha }_T$ is the coefficient of linear thermal expansion, $\lambda$, $\mu$ are Lamé’s constants, $c_1$ is the measure of thermo-diffusion effects, and ${\tau }_0$ is the thermal and mechanical relaxation times.

The equation of mass diffusion:

where $C$ is the concentration of the diffusive material, $B$ is the diffusion coefficient, $b$ is the measure of diffusive effects, ${\beta }_2=\left(3\lambda +2\mu \right){\alpha }_C$, ${\alpha }_C$ is the coefficient of linear diffusion expansion, and ${\tau }_1$ is the diffusion relaxation time.

The constitutive relations:

where $P$ is the chemical potential.

The strain-displacement relations:

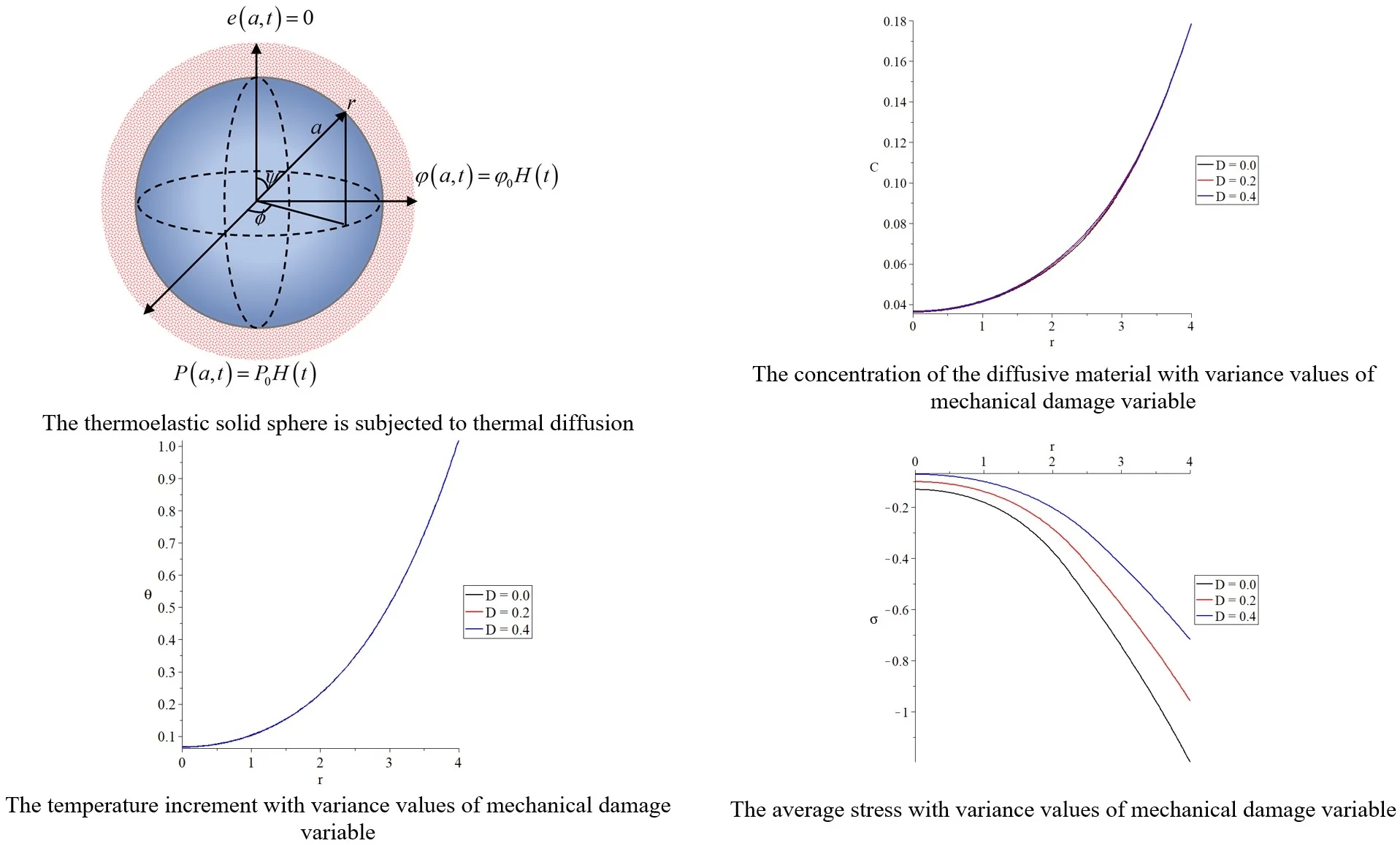
Let us assume a perfect thermoelastic, conducting, isotropic, and spherical medium occupies the space which is defined by $\mathrm{\Omega }=\left\{\left(r,\psi ,\varphi \right):0\le r\le a,0\le \psi \le 2\pi ,0\le \varphi <2\pi \right\}$. The spherical coordinate system $\left(r,\psi ,\varphi \right)$ will be applied to denote the radial coordinate, the co-latitude, and longitude of a spherical coordinate system, respectively, and initially quiescent where $r$ is the sphere's radius as in Fig. 1.

The condition of symmetry is satisfied If there are no latitudinal and longitudinal variations. Therefore, all the state-functions will depend on radial distance $r$ and time $t$.

Fig. 1The thermoelastic solid sphere is subjected to thermal diffusion

Due to the spherical symmetry, the components of displacements take the forms:

and the strain components are:

where $e$ defines the volumetric dilatation and takes the form:

The equations of motion under the mechanical damage and thermal diffusion considerations takes the form [1, 8-10]:

The constitutive equations with mechanical damage parameter [1, 8-10]:

The equation of heat conduction based on the Lord-Shulman theory takes the following form [1, 8-10]:

The mass diffusion equations take the forms [1, 8-10]:

and:

where ${\nabla }^2=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)$.

We assume that $\theta =\left(T-T_0\right)$gives the temperature increment. Hence, the Eqs. (12)-(15), (17)-(19) take the following forms:

The Eq. (20) could be changed to be in the form:

The following non-dimensional variables will be applied for convenience [10, 31]:

Then, we obtain:

where:

For more simple use, the primes have been suppressed.

The following Laplace operator ${\nabla }^2=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)$ has a singular point at $r=0$. Because the symmetry conditions prevail, the singularity problem is solved by using L’Hospital’s rule as follows [29]:

Then, we get:

which satisfy the boundary conditions:

By using the Eq. (36) in Eqs. (29)-(31), we get:

The Laplace transform which is defined as follows will be used:

where the initial conditions have been considered as follows:

Hence, the Eqs. (29)-(35) take the following forms:

where ${\alpha }_4=\frac{s^2}{3\left(1-D\right)}$, ${\alpha }_5=\frac{\left(s+{\tau }_0{s}^2\right)}{3}$, and ${\alpha }_6=\frac{\left(s+{\tau }_1{s}^2\right)}{3}$.

By making internal eliminations between Eqs. (43)-(45), we get:

where:

Thus, according to the boundary conditions Eqs. (37), the general solutions can be written in the forms:

where $\pm k_i$, $i=\mathrm{1,2},3$ are the roots or the solution of the characteristic equation:

and the constants $A_i,E_i,C_i$ must satisfy the relations Eqs. (43)-(45), thus, we have:

which gives:

Then, we have:

To get the constants $A_1$, $A_2$, and $A_3$, we must use the given boundary conditions at the position $r=a$. So, we consider that $r=a$ the sphere is thermally loaded by heat and chemical potential shocks as follows [9, 10]:

where $H\left(t\right)$ denotes the Heaviside unit step function and ${\phi }_o$, $P_0$ are constants.

Zero volumetric deformation at the position $r=a$ has been considered as the mechanical boundary as follows:

This condition means that the surface of the sphere is connected to a rigid foundation which can prevent any displacement.

By applying Laplace transform on the Eqs. (58)-(60), we get:

Substitute from Eqs. (61)-(63) into the Eqs. (46). Hence, we obtain:

where $C_0=\frac{{\alpha }_1{\phi }_0+P_0}{{\alpha }_3}$.

Substitute from the boundary conditions Eqs. (61), (63) and (64) into the Eqs. (52), (56) and (57), the following system has been obtained:

We obtain the constants $A_i$, $i=\mathrm{1,2},3$ by solving the above system as follows:

To find the displacement, the Eqs. (50), and (56) will be used as follows [29]:

The singularity problem in the relation Eqs. (68) can be solved by using L’Hospital’s rule as follows:

Hence, we have:

To find the stress in a simple form, the average of three principal stresses components on Eqs. (47)-(49) will be considered as follows:

To obtain all the studied functions in the time domain numerically, the Riemann-sum approximation techniques will be applied, where the Laplace transform of any function $\stackrel{-}{f}\left(r,s\right)$ could be inverted as follows [32]:

where “$Re$” is the real part and “$i$” is the well-known imaginary number unit. For a convergence with faster prosses, Tzou stated that the value $\kappa$must satisfy the relation $\kappa t\approx$ 4.7 [32]. MAPLE software has been used to formulate the Eq. (72) and to compute the temperature increment volume deformation, concentration, displacement, average stress, and chemical potential in the time domain.

3. Numerical results and discussion

The copper material has been taken as the thermoelastic material for which the following values of the physical constants have been taken [4, 7, 9, 10, 34]: $\mu =$ 3.86×10¹⁰ kg m^-1 s^-2, $\lambda =$ 7.76×10¹⁰ kg m^-1 s^-2, $\rho =$ 8954 kg m^-3, $c_E=$ 383.1 m² k^-1 s^-2, ${\alpha }_T=$ 1.78 10^-5 k^-1, $K=$ 386 kg m k^-1s^-3, ${\alpha }_c=$1.98 10^-4 m³ kg^-1, $B=$ 0.85×10^-8 kg s m^-3, $T_o=$ 293 k, $c_1=$ 1.2×10⁴ m² s^-2 K^-1, $b=$ 0.9×10⁶ m⁵ s^-2 kg^-1, $\eta =$ 8886.73 s m^-2.

Thus, the non-dimensional parameters take the following values: ${\alpha }_1=\text{5.48}$, ${\alpha }_2=$3.78×10^-4, ${\alpha }_3=\text{36.98}$, ${\epsilon }_1=$16.86×10^-3, ${\epsilon }_2=$ 92.15×10^-3, ${\beta }^2=$ 4, ${\phi }_0=$ 1.0, $P_0=$ 1.0, ${\tau }_0=$ 0.02, ${\tau }_1=$ 0.01.

The numerical results of the temperature increment, volumetric deformation, concentration, displacement, average stress, and chemical potential distributions will be shown in figures with a wide range of the dimensionless radial distance $r\left(0\le r\le 4.0\right)$ and at a dimensionless value of time $t=$ 1.0. Figs. 2-7 have been carried out for the temperature increment, concentration of the diffusive material, volumetric strain, displacement, average stress, and chemical potential, respectively, with various mechanical damage parameters when $D=$(0.0, 0.2, 0.4) where the value $D=$ 0.0 represents the undamaged state. In contrast, the values $D=$ 0.2, 0.4 represent the damage states.

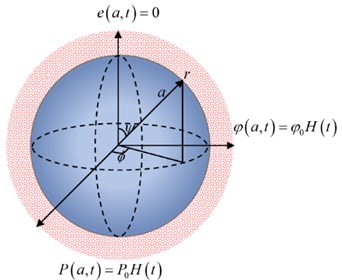
Fig. 2The temperature increment with variance values of mechanical damage variable

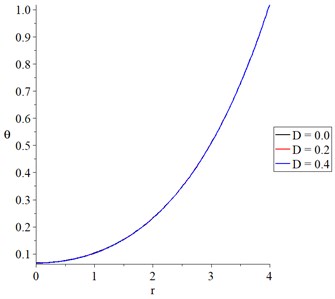
Fig. 3The concentration of the diffusive material with variance values of mechanical damage variable

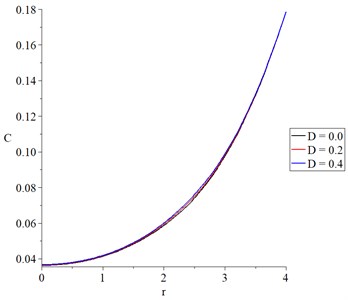
Fig. 2 represents the temperature increment distribution where the three curves have the same behaviors and begin with the same value $\phi \left(r=4.0\right)=1.0$, which agrees with the value of the thermal shock on the bounding surface of the sphere. It is noted that the mechanical damage parameter has a limited effect on the temperature increment distribution. The curve of the temperature increment falls to zero at the sphere center $r=0$, thus, the thermal wave has a finite speed of propagation.

Fig. 3 shows the concentration distribution where the three curves have the same behavior and begin with the same value $C\left(r=4.0\right)=$ 0.18. The value of the mechanical damage parameter has a limited effect on the concentration distribution. An increase in the mechanical damage parameter leads to a rise in the concentration distribution. The concentration curve falls to zero at the center $r=0$ which means the diffusion wave propagates with a finite speed.

Fig. 4The volumetric strain with variance values of mechanical damage variable

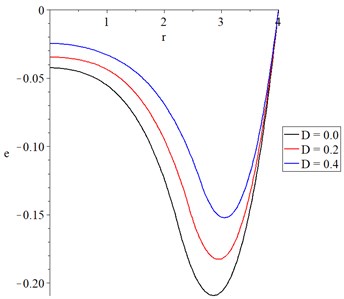
Fig. 5The displacement with variance values of mechanical damage variable

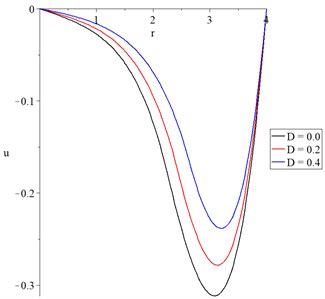
Fig. 4 represents the volumetric strain distribution. It is noted that the three curves have the same behaviors with different values. All the curves begin with the same value $e\left(r=4.0\right)=$ 0.0, which agrees with the mechanical boundary conduction. The parameter of the mechanical damage has a significant effect on the volumetric strain distribution. An increase in the mechanical damage parameter leads to a decrease in the absolute value of the volumetric strain. Each curve has a peak point in the following order:

Fig. 5 shows the displacement distribution, and it is noted that the three curves have the same behavior with different values and begin with the same value $e\left(r=4.0\right)=$ 0.0 which agrees with the mechanical boundary condition. The parameter of the mechanical damage has a significant impact on the displacement distribution. An increase in the mechanical damage parameter leads to a decrease in the absolute value of the displacement. Each curve has a peak point in the following order:

Fig. 6The average stress with variance values of mechanical damage variable

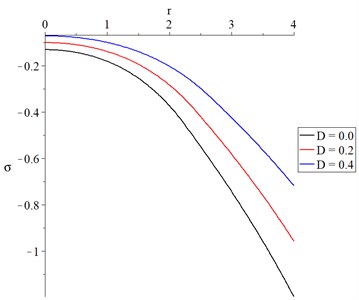
Fig. 7The chemical potential with variance values of mechanical damage variable

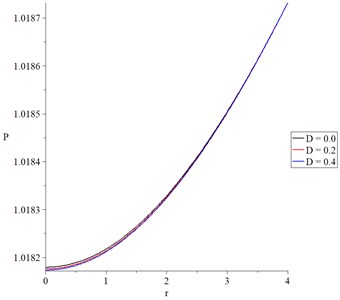
Fig. 6 represents the average stress distribution where three curves have the same behavior with different values. All the curves begin and end with different values. The mechanical damage parameter has a significant impact on the average stress distribution. An increase in the mechanical damage parameter leads to a decrease in the absolute value of the average stress.

Fig. 7 shows the potential chemical distributions in which the three curves have the same behavior with different values in the region $0\le r\le 2.5$. The mechanical damage parameter has significant effects on potential chemical distributions. An increase in the value of the mechanical damage parameter leads to a decrease in the chemical potential values.

Fig. 8The temperature increment distribution when D= 0.2

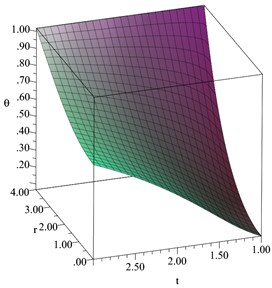
Fig. 9The concentration of the diffusive material distribution when D= 0.2

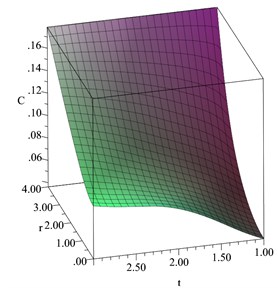
Fig. 10The volumetric strain distribution when D= 0.2

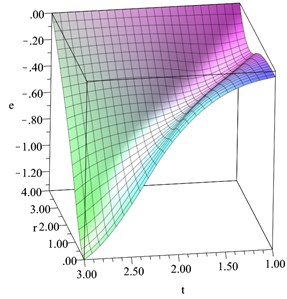
Fig. 11The displacement distribution when D= 0.2

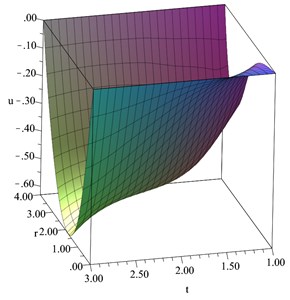
Fig. 12The average stress distribution when D= 0.2

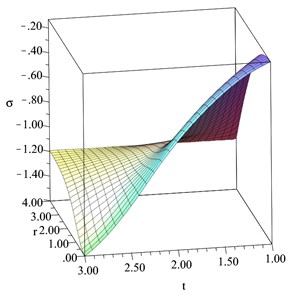
Fig. 13The chemical potential distribution when D= 0.2

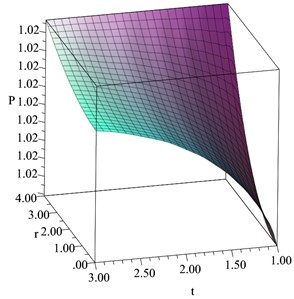
In 3-D, Figs. 8-13 show the distributions of the temperature increment, volumetric strain, concentration, displacement, average stress, and chemical potential distributions, respectively, when $D=$ 0.2. All the studied functions have been figured in a dimensionless wide range of the radial distance $r\left(0\le r\le 4.0\right)$ and a dimensionless wide range of the time $t\left(0\le t\le 3.0\right)$. It is shown that distance $r$ and time $t$ have significant effects on all the studied functions. An increase in the value of the time leads to an increase in all the studied functions, while an increase in the value of the distance along the radius of the sphere leads to a decrease in the values of all the studied functions.

Fig. 14-19 have been carried out for the temperature increment, concentration of the diffusive material, volumetric strain, displacement, average stress, and chemical potential, respectively, with various situations of relaxation times. ${\tau }_0={\tau }_1=0$ represents the studied functions distributions without thermal and diffusional relaxation time, ${\tau }_0=\text{0.08}$, ${\tau }_1=\text{0.04}$ represents the distribution of the studied functions when the value of thermal relaxation time is higher than the value of the diffusional relaxation time, and ${\tau }_0=\text{0.04}$, ${\tau }_1=\text{0.08}$ represents the distribution of the studied functions when the value of thermal relaxation time is smaller than the value of the diffusional relaxation time. The figures show that thermal and diffusional relaxation times have significant effects on all the studied functions.

Fig. 14The temperature increment with various values of thermal and diffusive relaxation times

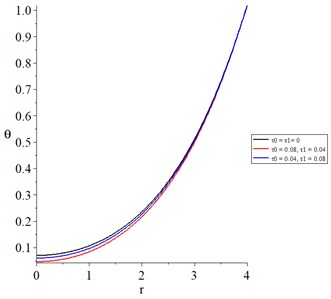
Fig. 15The concentration of the diffusive material with various values of thermal and diffusional relaxation times

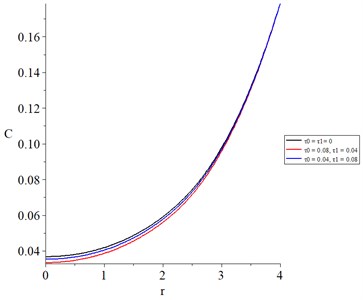
Fig. 16The volumetric strain with various values of thermal and diffusional relaxation times

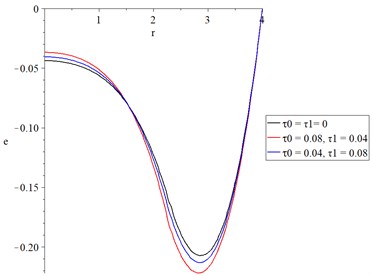
Fig. 17The displacement with various values of thermal and diffusional relaxation times

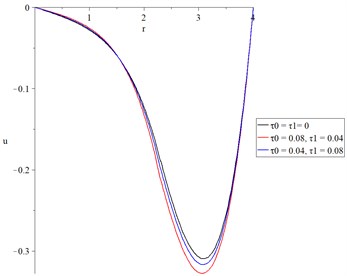
Fig. 14 shows the temperature increment, and its values take the following order:

Fig. 15 shows the concentration of the diffusive material, and its values take the following order:

Fig. 16 shows the volumetric strain distributions, and its peak points take the following order:

Fig. 17 shows the displacement distributions, and its peak points take the following order:

Fig. 18The average stress with various values of thermal and diffusional relaxation times

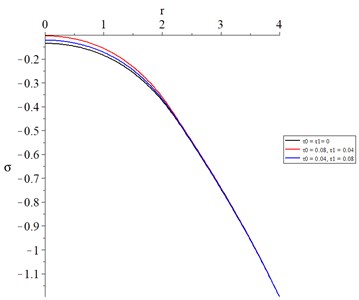
Fig. 19The chemical potential with various values of thermal and diffusional relaxation times

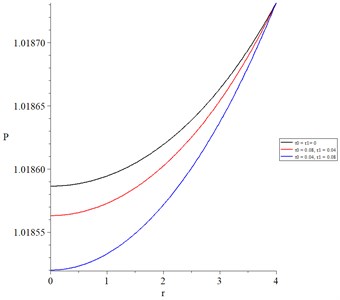
Fig. 18 shows the average stress distributions, and its endpoints take the following order:

Fig. 19 shows the potential chemical distributions, and take the following order:

For validation of the current results, we can see that some of the current results agree with the results of Aouadi [10].

4. Conclusions

The results of this work conclude that in the context of the Lord-Shulman model, the thermal, diffusional, and mechanical waves propagate with finite speeds.

Moreover, the mechanical damage variable, radial distance, and time significantly affect all the studied functions.

The thermal and diffusional relaxation times have significant effects on all the studied functions.

The mechanical damage variable does not affect the temperature increment distribution and has a small impact on the concentration and chemical potential distributions.

The mechanical damage variable has significant impacts on the volumetric strain, displacement, and average stress.