Abstract
Small scale parameter of graphene sheet is considered as uncertain one, vibration equation of a simply supported graphene sheet with uncertainty is established based on nonlocal theory. Trigonometric function series solution and interval operator are used to obtain the upper and lower bound of response of the simply supported graphene sheet. the uncertainty level of response for the different dimension is investigated. The numerical result shows that for the same uncertainty level of small scale parameter, the uncertainty level of the response will decrease with increase of the graphene sheet dimension, and a small uncertainty level of the small scale parameter can cause much greater uncertainty level of the response before the small scale effect disappears.
Highlights
- Comparison of the above maximum uncertainty level of the different dimension graphene sheet can be concluded that for the same uncertainty level of small scale parameter, the uncertainty level of the response will decrease with increase of the graphene sheet dimension.
- It is found that a small uncertainty level of the small scale parameter can cause much greater uncertainty level of the response before the small scale effect disappears.
- We found from the previous study [15] that the small scale effect will disappear if the side lengths of the graphene sheet are both larger than 1um, the result is agreement with that given in this paper.
1. Introduction
With the development of nano mechanical and electrical technology, the mechanical properties of nanoscale structures to cause the considerable attention of many scholars. The small scale effect is found during study of nano structures. Due to the surface effect and the small-scale effect of nanomaterials, classical continuum mechanics will lead to an inaccurate result when it is used to solve the mechanics problem of nanomaterials. Fortunately, the nonlocal theory given by Eringen [1] can remove the shortcoming of classical continuum mechanics. Based on the nonlocal theory, Zhang, Liu, and Wang [2] studied the buckling of multi-walled carbon nanotube. Xie, Han, and Long [3-5] investigated the small scale effect and the vibration of carbon nanotube. Wang [6] used a modified nonlocal beam model to study vibration and stability of nanotubes conveying fluid. Hybrid nonlocal beam model [7] was employed to study bending, buckling, and vibration of micro/nanobeams. Liang Y. and Han Q. [8] gave prediction of the nonlocal scaling parameter for graphene sheet. L Yang,J S Peng [9] used the nonlocal-gradient elasticity theory to scale effect on dynamic analysis of electrostatically actuated nano beams. Hamid M. et al. [10] studied the size dependent static and dynamic pull-in instability of cantilever nanoactuator based on strain gradient theory. Fang B., Zhen Y. X., Zhang C. P., et al. [11] carried out nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Reddy J. N. [12] presented nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. M. Ghalambaz [13] used energy balance method to investigate nonlinear oscillation of nanoelectro-mechanical resonators.
In previous studies, the parameters of the graphene sheet are deterministic. However, until now, the deterministic small scale parameter of the graphene sheet has been given. This will lead to the uncertain dynamic response of the graphene sheet.
In this paper, a nonlocal model of nanoplate is developed for vibration of a simply supported graphene sheet with uncertainty. The upper and lower bound of response of a clamped graphene sheet is obtained, and the uncertainty level of response is also obtained.
2. Formulation
2.1. Nonlocal constitutive equation
The nonlocal constitutive equations of graphene [2] are:
where is the elastic modulus of graphene, and Poisson’s ratio, an internal characteristic length (C-C bond length), a constant appropriate to each material considered as the uncertain parameter.
Eq. (1) can be approximately expressed as:
2.2. Geometric equations
Eringen [1] proposed the nonlocal theory in which the nonlocality of stress is mainly considered and strain is remained the same as the classical. three displacement components can be expressed in terms of the deflection based on the Kirchhoff assumption. The relationship between the three components of strain and deflection can be given by:
2.3. The governing equation of motion
Hamilton principle is used to establish the governing equation of motion, mathematically, Hamilton principle states:
where is Lagrangian function. is given as:
where is the kinetic energy, the strain energy, and the work done by the external forces.
The kinetic energy is given by:
where is the mass density of unit area, stands for the whole area of the graphene sheet.
The strain energy of the graphene sheet can be expressed as:
The work done by the external force can be obtained by:
where is the distribution force on the upper surface of the graphene sheet, stands for damping coefficient.
Substitution of Eqs. (5)-(8) into Eq. (4) yields the governing equation of motion:
where is the flexural rigidity , thickness of the graphene sheet.
2.4. Solution of the governing equation of motion
Transient response of Eq. (9) satisfying the simply supported boundary can be given by:
where and denote the length and width of the graphene sheet, respectively.
Substitution of Eq. (10) into Eq. (9) yields the transient response:
where damping frequency :
The undamped natural frequency :
Damping ratio :
The initial condition:
Combination of Eq. (15) with Eq. (11), has:
Transient response:
Let a harmonic excitation is applied on the graphene sheet, the steady response of the graphene sheet can be adopted as the following form:
Substituting Eq. (19) and into Eq. (9) and then solving Eq. (9) based on orthogonal property of trigonometric function yields:
where:
The total response is:
2.5. Interval analysis of vibration response
Let is an interval variable, the upper and lower bound of can be expressed as:
where is the midpoint value of , the interval radius of .
The interval variable is between the upper and lower bound:
can be expanded into Taylor series:
The midpoint value of response :
The interval radius of response :
3. Numerical example
For all the subsequent numerical example, the length of C-C bond 0.142×10-9 m, in-plane stiffness 360 J/m2 (Sanchez -Portal,D, [14]), Poisson’s ratio 0.26, the thickness of the graphene sheet 0.34×10-9 m, the mass density of unit area 0.77×10-3 kg/m2, the damping coefficient 0.3 Ns/m. The initial velocity , the initial deflection 5×10-9 m.
Let is an interval variable, the uncertainty level ±3 % off from the midpoints 0.39, investigated. The amplitude of load is 300 nN/m2, the uncertainty level of response for the different dimension graphene sheet is investigated.
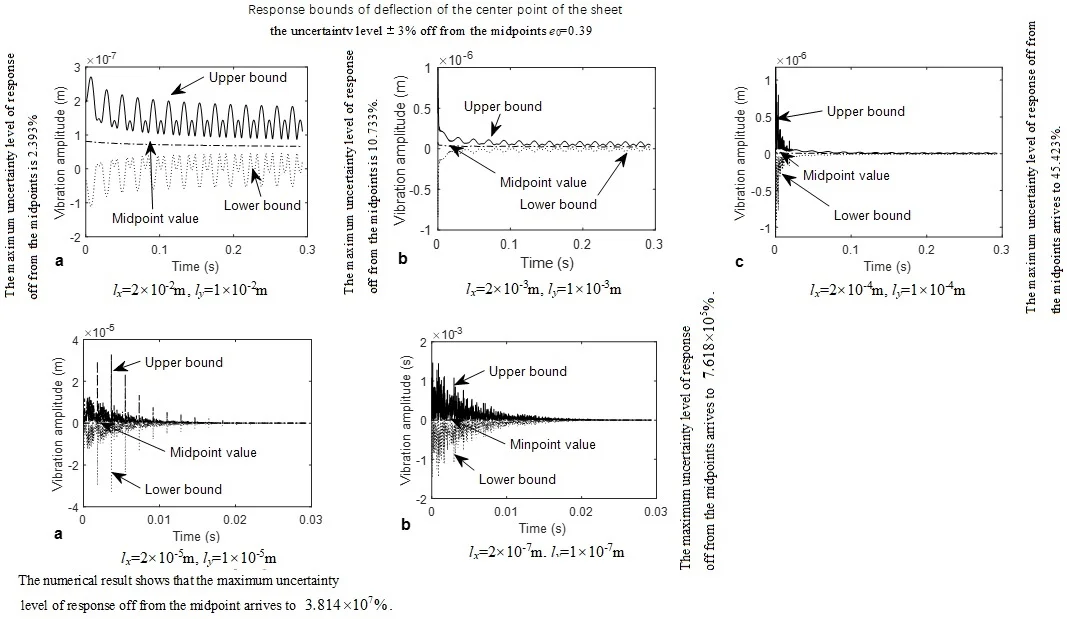
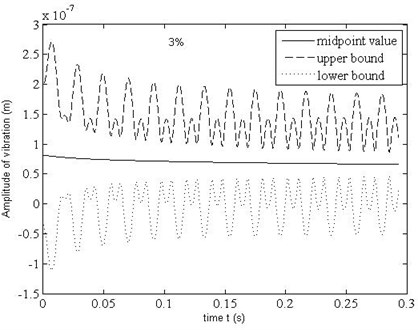
Dynamic response bounds of deflection of the center point of the sheet 2×10-2 m, 1×10-2 m) is shown in Fig. 1(a). From this figure, it can be found that the amplitude of vibration of the sheet obeys law of exponent decay. The maximum uncertainty level of response off from the midpoints is 2.393 %. The maximum uncertainty level of response is smaller than the uncertainty level ±3 % of .
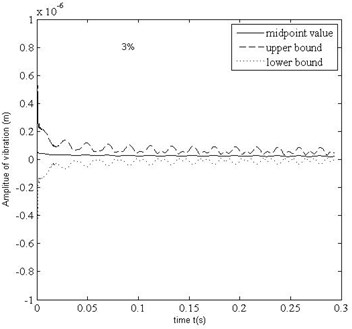
Dynamic response bounds of deflection of the center point of the sheet ( 2×10-3 m, 1×10-3) mis shown in Fig. 1(b). From this figure, it can be found that the amplitude of vibration of the sheet obeys law of exponent decay. The maximum uncertainty level of response off from the midpoints is 10.733 %. The maximum uncertainty level of response is 3 times more than the uncertainty level ±3 % of .
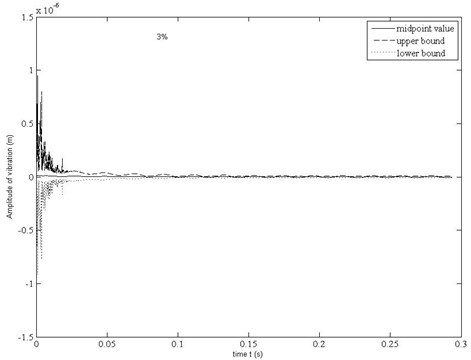
Dynamic response bounds of deflection of the center point of the sheet ( 2×10-4 m, 1×10-4 is shown in Fig. 1(c). From this figure, it can be found that the amplitude of vibration of the sheet obeys law of exponent decay. The maximum uncertainty level of response off from the midpoints arrives to 45.423 %. The maximum uncertainty level of response is 15 times more than the uncertainty level ±3 % of .
Fig. 1Response bounds of deflection of the center point of the sheet
a) 2×10-2 m, 1×10-2 m
b) 2×10-3 m, 1×10-3 m
c) 2×10-4 m, 1×10-4 m
Fig. 2Response bounds of deflection of the center point of the sheet
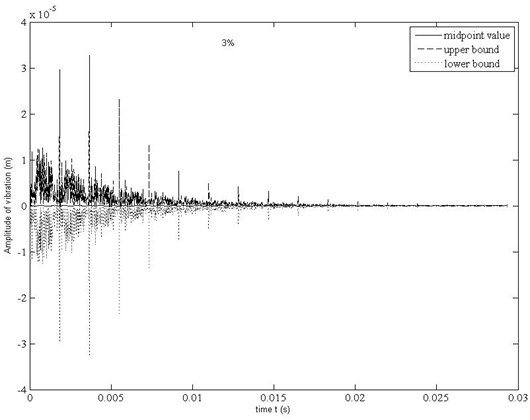
a) 2×10-5 m, 1×10-5 m
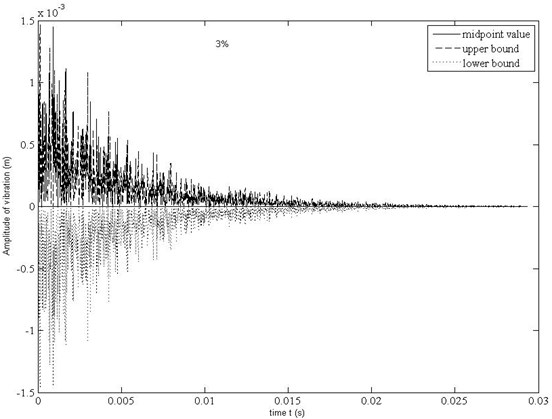
b) 2×10-7 m, 1×10-7 m
Dynamic response bounds of deflection of the center point of the sheet ( 2×10-5 m, 1×10-5 m) is shown in Fig. 2(a). It can be seen that amplitude of the sheet overall presents the attenuation trend. The maximum uncertainty level of response off from the midpoints arrives to 7.618×105 %.
Dynamic response bounds of deflection of the center point of the sheet ( 2×10-7 m, 1×10-7 m) is shown in Fig. 2(b). From this figure, it can also be found that amplitude of the sheet overall presents the attenuation trend. The numerical result shows that the maximum uncertainty level of response off from the midpoints arrives to 3.814×107 %.
4. Conclusions
Comparison of the above maximum uncertainty level of the different dimension graphene sheet can be concluded that for the same uncertainty level of small scale parameter, the uncertainty level of the response will decrease with increase of the graphene sheet dimension. We found from the previous study G. Q. Xie [15] that the small scale effect will disappear if the side lengths of the graphene sheet are both larger than 1×10-7 m. Here we found that a small uncertainty level of the small scale parameter can cause much greater uncertainty level of the response before the small scale effect disappears.
The result that the small scale effect will disappear if the side lengths of the graphene sheet are both larger than 1×10-7 mis valuable and very helpful for the design and manufacture of graphene and CNT devices are of guiding significance.
References
-
Eringen A. C., Edelen Gb D. On nonlocal elasticity. International Journal of Engineering, Vol. 10, 1972, p. 233-248.
-
Zhang Y. Q., Liu G. R., Wang J. S. Small scale effects on buckling of multi-walled carbon nanotubes under axial compression. Physical Review B, Vol. 70, 2004, p. 205430.
-
Xie G. Q., Han X., Liu G. R., Long S. Y. Effect of small size scale on the radial buckling pressure of a clamped multi-walled carbon nanotube. Smart Materials and Structures, Vol. 15, 2006, p. 1143-1149.
-
Xie G. Q., Long S. Y. Elastic vibration behaviors of carbon nanotubes based on micropolar mechanics. Computers, Materials and Continua, Vol. 4, Issue 2, 2006, p. 11-20.
-
Xie G. Q., Han X., Long S. Y. The effect of the small size on dispersion characteristics of the carbon nanotube. International Journal of Solid and Structure, Vol. 44, 2007, p. 1242-1255.
-
Wang L. A modified nonlocal beam model for vibration and stability of nanotubes conveying fluid. Physica E: Low-dimensional Systems and Nanostructures, Vol. 44, Issue 1, 2011, p. 25-28.
-
Zhang Y. Y., Wang C. M., Challamel N. Bending, buckling, and vibration of micro/nano beams by hybrid nonlocal beam model. Journal of Engineering Mechanics, Vol. 136, Issue 5, 2009, p. 562-574.
-
Liang Y., Han Q. Prediction of the nonlocal scaling parameter for grapheme sheet. European Journal of Mechanics – A/Solids, Vol. 45, 2014, p. 153-160.
-
Peng J. S., Yang L., Yang J. Size effect on the dynamic analysis of electro statically actuated micro-actuators. Microsyst Technol, Vol. 23, 2017, p. 1247-1254.
-
Hamid Sedighi M., Koochi A., Abadyan M. Modeling the size dependent static and dynamic pull-in instability of cantilever nanoactuator based on strain gradient theory. International Journal of Applied Mechanics, Vol. 6, Issue 5, 2014, p. 1450055
-
Fang B., Zhen Y. X., Zhang C. P., et al. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Applied Mathematical Modeling, Vol. 37, Issue 3, 2013, p. 1096-1107.
-
Reddy J. N. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. International Journal of Engineering Science, Vol. 48, Issue 11, 2010, p. 1507-1518.
-
Ghalambaz M., Ghalambaz M., Edalatifar M. Nonlinear oscillation of nanoelectro- mechanical resonators using energy balance method: considering the size effect and the van der Waals force. Applied Nanoscience, Vol. 6, 2016, p. 309-317.
-
Sanchez Portal D., et al. A initio structural, elastic, and vibrational properties of carbon nanotubes, Physical Review B, Vol. 59, 1999, p. 12678-12688.
-
Xie Genquan, Wang Jianping, Zhang Qilong Small scale effect of a simply supported graphene sheet’s dynamic response. Journal of Vibration and Shock, Vol. 37, Issue 15, 2018, p. 277-282.
About this article
This work is supported by National Natural Science Foundation of China under the Grant Number 11372109.
