Influences of physical and structural parameters on vibration modes for large-scale rotating wind turbine blades

1. Introduction

As environment and energy issues become increasingly prominent, governments and enterprises from all over the world pay more and more attention to the wind energy, which is an inexhaustible, nonpolluting and renewable energy [1]. Wind power generation is one of the main forms of wind energy utilization, while engineering practice indicates that the wind turbine blade is the most prone to malfunction. This is because the aerodynamic load acting on the blade and the centrifugal force generated by the rotation are constantly changing, and they have apparent polytropy and random [2]. When the changing frequency of wind loading, the rotating frequency of the blade and the frequency of the generator are close to the natural one of the blade structure, it's possible that the strong vibration or even the resonance for the blade will appear, which leads to the fatigue damage and the failure of mechanism, not making the blade operate safely and stably. Therefore, it’s significant to calculate and analyze the vibration modes of the blade.

Mode is an inherent vibration characteristic of mechanical structure. At present, the modal parameters of the structure such as the natural frequencies and mode shapes have been studied by using the finite element method and the experimental method. Kane et al. [3] found the phenomenon that the lateral vibration frequency of a cantilever beam attached to a moving base increased when it rotated, and put forward the concept known as dynamic stiffening. Wang and Pei [4] took the agricultural wind turbine blade for example, and analyzed the inherent vibration characteristics including flap, flutter and torsion using ANSYS. Gangeled and Ahmed [5] carried out the analysis on the natural frequency and mode shape of 1.5 MW wind turbine blade under different geometrical and material parameters without considering the dynamic stiffening effect, and then investigated the dynamic behavior characteristic of the blade. Tarfaoui et al. [6] completed the modal analysis of the 5 MW composite wind turbine blade by using ABAQUS and presented five different types of strength enhancement structure, and a comparative analysis of the various structures was carried out to select the optimal scheme to realize the lightweight of the blade. Benham et al. [7] optimized the NACA 4412 profile and performed the modal and static analysis of the blades made of carbon fiber and other three kinds of composite materials. Chen et al. [8] employed Wilson theory to develop an application program for aerodynamic design of the small blades, designed a 3 kW horizontal wind turbine blade and analyzed the influence of the material manufacturing deviation on natural vibration characteristic of the static blade. Wu et al. [9] used Wilson aerodynamic theory to design a 100 W horizontal axis blade, modified design parameters by considering vibration performance and carried out modal and pneumatic characteristic experiments. Li et al. [10] applied the Multi-body dynamics method to discuss the reason for the stiffening effect of rotating blades and analyzed the influence of the GRP anisotropy on the vibration modes of the blade.

Although there are some research advances in the analysis of the vibration modes of the wind turbine blade at home and abroad, the research on the influences of the material and its manufacturing deviations on the natural vibration characteristics of the blade under the rotating condition has not been carried out until now. To solve this problem, the dynamic characteristic equation and the entity model of the rotating blade were established in this study, and then the grid independence and the reliability verification were carried out. Furthermore, the effects of the rotating speed, material categories and different physical and structural parameters for the same material on the blade vibration modes were simulated and analyzed.

Through the modal analysis of the wind turbine blade in this work, it’s easy to check whether the resonance mode of the system is reached under different working conditions, and evaluate the influences of the possible existence of material manufacturing deviations on the safety and reliability of large-scale wind turbine blades. The change law of the blade's modal frequency with elasticity modulus and mass density is presented in this work. In the design process of the blade, the elastic modulus and mass density of the material can be taken as the main reference to select the appropriate blade material which meets the design requirements. Furthermore, under the rated rotating speed which is the most common and frequent operating condition, the natural frequencies of the blades for different materials are shown and compared, providing significant guidelines for the selection of the blade’s material.

2. Dynamic characteristic equation of the blade

After the blade is discretized by the finite element method, the motion differential equation of the structure can be obtained by using the principle of the instantaneous minimum potential energy [11]:

where $\{$u$\}$, $\left\{\dot{\mathbf{u}}\right\}$ and $\left\{\ddot{\mathbf{u}}\right\}$ are the displacement, the velocity and the acceleration of the finite element node respectively. $\left\{\mathbf{F}\right\}$ is the external force vector acting on the blade. $\left[\mathbf{M}\right]$ and $\left[\mathbf{C}\right]$ are respectively the mass matrix and the damping matrix. Stiffness matrix $\left[\mathbf{K}\right]=\left[{\mathbf{K}}_0\right]+\left[{\mathbf{K}}_a\right]$, $\left[{\mathbf{K}}_0\right]$ and $\left[{\mathbf{K}}_a\right]$ represent the finite element stiffness matrix for small deformation and the dynamic stiffness matrix respectively.

When the wind turbine blade rotates around the rotating shaft in a certain angular velocity, the centrifugal inertia force has an effect on the blade deformation, and the mutual coupling between the rotation and deformation leads to the change of the blade stiffness, which is known as dynamic stiffening phenomenon [12]. While calculating the vibration modes of the rotating blade, the dynamic stiffness matrix can be expressed as:

where $\left[{\mathbf{K}}_s\right]$ is the stress stiffness matrix generated by the mutual coupling between the blade rigid motion and its elastic deformation, and $\left[{\mathbf{K}}_g\right]$ is the geometric stiffness matrix resulted from the in-plane deformation which is caused by the centrifugal inertia force.

In Eq. (1), set $\left\{\mathbf{F}\right\}=\left\{0\right\}$, and then the blade is in free vibration state at this time. In addition, when solving the natural frequency of the blade structure, the damping effect is generally not considered, that is, $\left[\mathbf{C}\right]=\left[0\right]$. Therefore, Eq. (1) can be rewritten as:

Assume $\left\{\mathbf{u}\right\}=\left\{{\mathbf{\varphi }}_i\right\}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{i}t$ and substitute it into Eq. (3), and then the generalized eigenvalue equation of the structural dynamic problem for the blade can be described as:

where ${\omega }_i$ and $\left\{{\varphi }_i\right\}$ are the eigenvalue and the eigenvector at the $i$ order respectively, and they are corresponding to the natural frequency and mode shape of the blade structure. Moreover, ${\omega }_i=2\pi f_i$, and $f_i$ is the self-vibration frequency.

3. Numerical simulation process

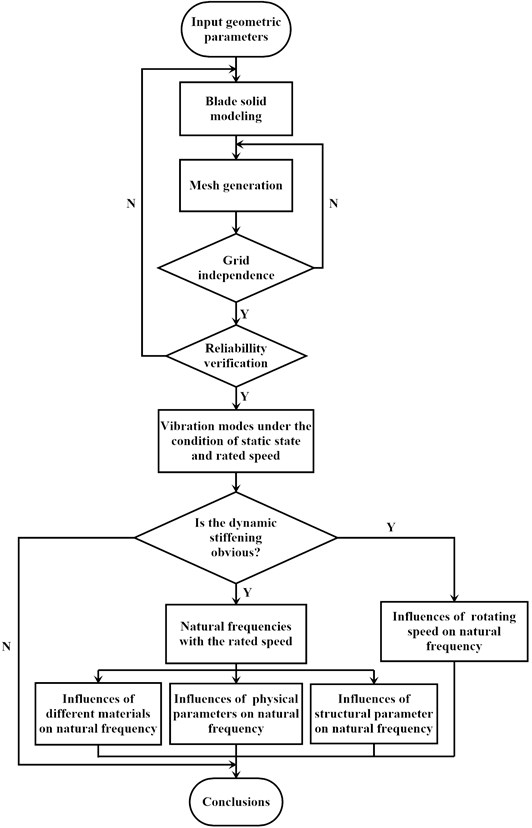
The influences of the rotating speed, different materials, and physical and structural parameters of the same material on the vibration modes for the blade under the rotating condition were analyzed in this work. The main steps are as follows: 1) The geometrical parameters of each blade element for the 5 MW offshore wind turbine, such as airfoil, chord Length and torsional angle, were obtained from the technical report released by the National Renewable Energy Laboratory (NREL), and the entity model of the blade was built by Unigraphics NX (UG). 2) The mesh generation for the entity model was carried out until the requirement for the grid independence was satisfied. 3) Compare and analyze the accuracy of the natural frequencies to verify the reliability of the numerical simulation results in this study. 4) By comparing the natural frequencies under the condition of rated rotating speed and static state, one can judge whether the dynamic stiffening effect is considered or not. 5) Give the change rules of natural frequency at each order varying with rotating speed. 6) Under the rated rotating speed, compare the natural frequencies of each order for different materials, and analyze the influences of different physical parameters of the same material and the variation of the structural parameter on the blade vibration modes. The detailed process of numerical simulation is shown in Fig. 1.

Fig. 1Flow chart of numerical simulation

4. Entity modeling and mesh generation of the blade

4.1. Entity modeling

Taking a wind turbine blade with the current installed capacity of 5MW as the research object, Ref. [13] gave the corresponding geometric data of the airfoil profile. The specific parameters are listed in Table 1. The airfoil coordinates were transformed, and UG was used to establish blade elements and curved surfaces, and then the blade solid model was built with the aid of the curve group function, as shown in Fig. 2.

Table 1Parameters of blade elements

No.	Span (m)	Chord length (m)	Torsional angle (°)	Airfoil
1	2.8667	3.542	13.308	Cylinder
2	5.6000	3.854	13.308	Cylinder
3	8.3333	4.167	13.308	Cylinder
4	11.7500	4.557	13.308	Cylinder
5	15.8500	4.652	11.480	DU40_A17
6	19.9500	4.458	10.162	DU35_A17
...	...	...	...	...
14	52.7500	2.518	1.526	NACA64_A17
15	56.1667	2.313	0.863	NACA64_A17
16	58.9000	2.086	0.370	NACA64_A17
17	61.6333	1.419	0.106	NACA64_A17

Fig. 2Entity model for the wind turbine blade

5. Results and discussions

5.1. Reliability verification

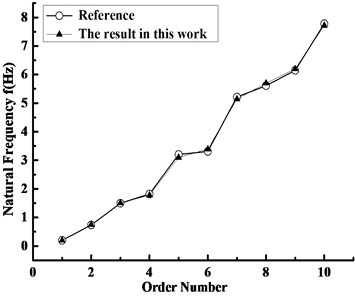
The 30 kW wind turbine blade model in Ref. [8] was selected to carry out reliability verification. The diameter of the wind wheel is 10 m, and the airfoil of the blade made of pine is NACA4412. The comparison results of the natural frequencies for the first ten orders are displayed in Fig. 4. It is very clear that the two variation curves of the natural frequency vs. the order number show a good agreement, which verifies the reliability of theoretical model and calculation program in this work.

Fig. 3Finite element model for the 5 MW wind turbine blade

Fig. 4Variation of the blade natural frequency with order number

5.2. Influences of rotation on vibration modes

5.2.1. Modal analysis of the static blade

The dynamic performance is significant to the design of the wind turbine blade. When the natural frequency of the blade is close to that of the excitation force, the resonance phenomenon will happen [14]. Thus, the modal analysis of the single blade was carried out in this work. Under the circumstances that the root of the GRP blade is fixed and the rotating speed was zero, the natural frequencies and mode shapes of the first ten orders were given in Table 3.

Table 3Natural frequencies and mode shapes of the first ten orders

Order number	Frequency ($\mathrm{H}\mathrm{z}$)	Mode shape
1st	0.3745	Flapping
2nd	1.0217	Flapping, Shimmy
3rd	1.1999	Flapping, Shimmy
4th	2.4117	Flapping
5th	3.4138	Shimmy
6th	4.3214	Flapping
7th	6.7048	Flapping
8th	7.5585	Obvious Shimmy
9th	9.6499	Flapping
10th	10.4260	Obvious Torsional Vibration

It can be seen from Table 3 that the mode shape of the first order is a pure flapping one, while the mixed form of flapping and shimmy appears in the second and the third orders. From the fourth to the ninth order, the blade basically keeps the mode shape of flapping or shimmy. The torsion mode shape appears in the tenth order, which indicates that the blade has strong anti-bending ability. According to the vibration theory, the energy of the blade vibration mainly concentrates on natural frequencies ranging from the first to the third order. Therefore, flapping and shimmy are the main vibration types of the wind turbine blade.

5.2.2. Modal analysis of the rotating blade

Under the condition of the rated rotating speed 12.1 rpm, the natural frequencies and the main mode shapes of the first ten orders were obtained, and the other conditions were identical to those of the static state. To observe the effects of the dynamic stiffening resulted from the blade rotation, the natural frequencies under static and rated rotating states are both listed in Table 4, as well as their relative errors. It can be found from Table 4 that the dynamic stiffening effect only has a significant influence on the blade natural frequencies of the first and the tenth order. What’s more, it is not obvious for the natural frequencies from the second to the ninth order, but all of them have some increase. Furthermore, the main mode shapes of the blade are plotted in Fig. 5. It can be directly seen that there are four mode shapes such as flapping, flapping and shimmy, shimmy and torsion, which is basically consistent with those of the static blade.

Table 4Natural frequencies of the first ten orders under rotating and static states (Hz)

Order number	1st	2nd	3rd	4th	5th	6th	7th	8th	9th	10th
Static	0.3745	1.0217	1.1999	2.4117	3.4138	4.3214	6.7048	7.5585	9.6499	10.4260
Rotating	0.1954	1.0276	1.2110	2.4319	3.5055	4.3751	6.8218	7.8030	9.9244	20.346
Relative Error	91.66	0.58	0.93	0.84	2.69	1.24	1.75	3.23	2.84	95.15

Fig. 5Main mode shapes of the blade under rated rotating speed

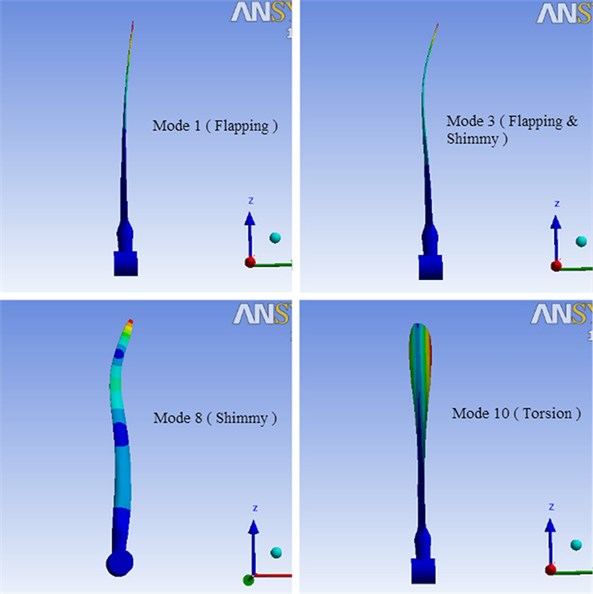
Table 5Natural frequencies of the first ten orders under different rotating speeds (Hz)

Rotational speed (rpm)	3.5	6.9	9.5	12.1	15.0	20.0
1st	0.3393	0.2742	0.2302	0.1954	0.1656	0.1298
2nd	1.0313	1.0293	1.0283	1.0276	1.0271	1.0267
3rd	1.2144	1.2126	1.2116	1.2110	1.2105	1.2101
4th	2.4332	2.4325	2.4321	2.4319	2.4317	2.4314
5th	3.5065	3.5060	3.5057	3.5055	3.5054	3.5053
6th	4.3755	4.3753	4.3751	4.3751	4.3750	4.3750
7th	6.8216	6.8216	6.8217	6.8218	6.8218	6.8221
8th	7.8028	7.8029	7.8029	7.8030	7.8030	7.8031
9th	9.9240	9.9242	9.9243	9.9244	9.9245	9.9248
10th	11.6300	14.4480	17.243	20.3460	24.0240	30.669

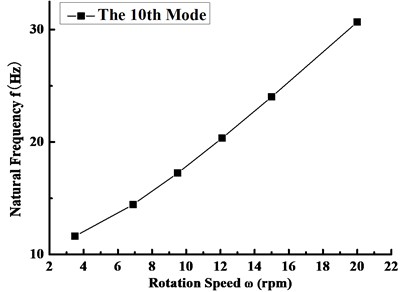
On the basis of this, the blade natural frequencies of the first ten orders under different rotating speeds are shown in Table 5. It can be found by comparing Table 5 with Table 3 that the variation trend of the natural frequency with the order number at each rotating speed is identical with that of Table 4. Furthermore, with the increase of the rotating speed, natural frequencies from the first to the sixth order for the rotating blades are all presenting a nonlinear decrease, and the reduction of the first order frequency has a certain representation, as shown in Fig. 6. This change trend is mainly derived from the stiffness weakening effect caused by the coupling between the rigid body motion and the elastic deformation of the blade, and the reduction of the stress stiffness at this time plays a dominant role. On the contrary, the natural frequencies from the seventh to the tenth order increase with the rotating speed, and the vibration of the tenth order natural frequency is the most obvious, as shown in Fig. 7. The reason is that the in-plane deformation resulted from the centrifugal inertia force makes the blade stiffness increase. At this very moment, the increase of the geometric rigidity is dominant, which leads to a slow upward trend of natural frequency.

Fig. 6Variation curve of the first order frequency with the rotating speed

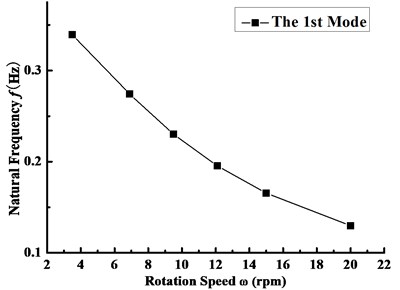
Fig. 7Variation curve of the tenth order frequency with the rotating speed

Obviously, the dynamic stiffening effect has a greater influence on the natural frequency. Therefore, the main work of this study is carried out aiming at the blade under the rotating condition.

5.4. Influences of material physical parameters deviation on natural frequencies

In the blade manufacturing process, the material physical properties have a certain randomness [14]. Therefore, the extensive use of GRP material was taken as an example in this work, and the influences of a certain range of the deviation in elasticity modulus and mass density on the blade natural frequency were analyzed.

Fig. 8Variation of the blade natural frequency vs. the order number with different materials

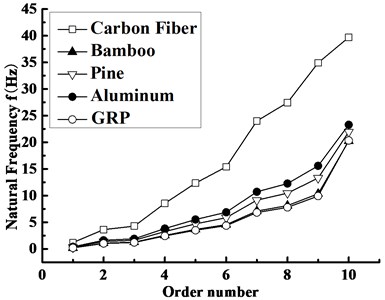
Fig. 9Natural frequencies of the blade with different elasticity modulus

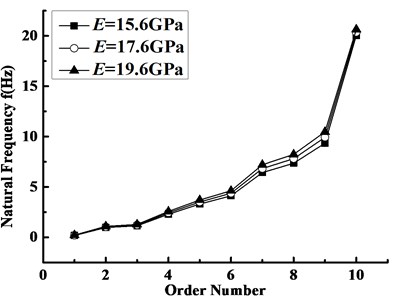
5.4.1. Deviation of elasticity modulus

The blade natural frequencies of the first ten orders within a certain deviation scope in elasticity modulus $\mathrm{E}$ were given in Fig. 9. As you can see, when the elastic modulus increases equally, the difference value between the natural frequencies first increases and then decreases with the increase of the order number, and reaches a maximum at the ninth order. This can be interpreted as the reason that the increase of the elasticity modulus causes the increase of stiffness, and then results in the rise of the natural frequency, while there is an obvious torsional vibration at the tenth order.

5.4.2. Deviation of mass density

Similar to Fig. 9, Fig. 10 also depicts the influences of the deviation in mass density $\mathrm{\rho }$ on the natural frequency. It can be observed from Fig. 10 that the deviation of mass density has a certain influence on the blade natural frequencies. When the density decreases equally, the difference between the natural frequencies shows the same trend with elasticity modulus shown in Fig. 9. The reason is that the density decrease brings about the mass reduction, which leads to the increase of the natural frequencies. Furthermore, the torsional vibration appeared at the tenth order renders the decrease of the increased amplitude of the natural frequency.

5.4.3. Influence of structural parameter on natural frequencies

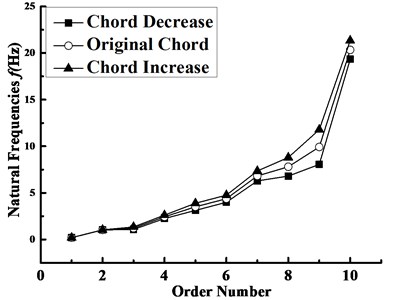
The design of the blade chord length is related to working efficiency, production cost, safety and many other aspects. Therefore, keeping GRP physical parameters constant, the chord length of each blade element group in Table 1 was increased or decreased 0.1 m, making the blade structure parameters change. For different chord lengths, the variation of the blade natural frequency with the order number is displayed in Fig. 11. With the chord length increasing equally, the increased amplitude of the natural frequency also reveals the same variation law with elasticity modulus, but there exists the other potential cause, that is, because the change of the blade chord length has a bigger effect on the stiffness than the mass, which results in the increase of the natural frequency. In addition, the chord length change has a more obvious impact on the shimmy and flapping frequencies of the first nine orders than the torsional one of the tenth order.

Fig. 10Natural frequencies of the blade with different mass densities

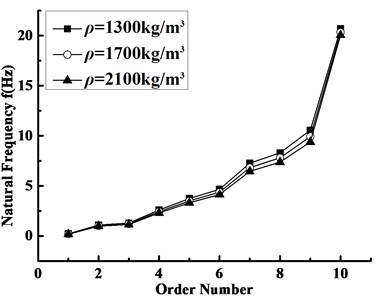
Fig. 11Natural frequencies of the blade with different chord lengths

6. Conclusions

In this work, the vibration modes of the 5MW wind turbine blade under different rotating speeds, material categories and manufacturing deviations of the material physical parameters and different chord lengths are numerically simulated and analyzed. The conclusions are summarized as follows:

1) With the increase of the rotating speed, the coupling effect of the rigid body motion and the deformation for the blade leads to the decrease of the natural frequencies from the first to the sixth order, while the centrifugal force results in the increase of the natural frequencies from the seventh to the tenth order. Hence, their combined effects should be considered under different working conditions and which factor plays a dominant role is ought to be analyzed. Only in this way can the vibration characteristic of the rotating blade be accurately reflected.

2) With the increase of the order number, the blade natural frequency basically presents a non-linear growth trend, and the changes of elasticity modulus, mass density and chord length make the difference value between the natural frequencies first increase, then decrease, and reach the peak value at the ninth order. Physical parameters and chord length have a greater impact on the shimmy and flapping frequencies of the first nine orders than the torsional one of the tenth order.

3) It is necessary to consider the influences of the dynamic stiffening effect and material manufacturing deviation simultaneously in the design of the natural frequency for wind turbine blades to avoid the structural instability phenomenon, which has a significant reference value to the blade safe operation.