Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Li, Qing-Lu; Luan, Wei-Di; Zhu, Zuo-Quan

doi:10.21595/jve.2017.17815

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2017

Check for updates

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Qing-Lu Li¹

Wei-Di Luan²

Zuo-Quan Zhu³

^{1, 2, 3}Department of Engineering Mechanics, Lanzhou University of Technology, Lanzhou, Gansu 730050, P. R. China

Corresponding Author:

Qing-Lu Li

Cite the article Download PDF

Downloads 1527

WoS Core Citations 8

CrossRef Citations 8

Abstract

This paper presents a free vibration analysis of functionally graded Reissner-Mindlin circular plates with various supported boundaries in thermal environments. A FGM consisting of metal and ceramic was considered in the study. Based on the geometric equation, physical equation and equilibrium equation of thick plate, taking into account the transverse shearing deformation, the free vibration equation of the axisymmetric FGM moderately thick circular plates was derived in terms of the middle surface angles of rotation and lateral displacement. The material properties of the plate were assumed to vary continuously in the thickness direction according a power law. By using shooting method to solve the coupled ordinary differential equations with different boundary conditions, the natural frequencies of FGM thick circular plates were obtained numerically. The effects of material gradient property, thickness ratio and boundary conditions on the natural frequencies were discussed in detail.

1. Introduction

Functionally graded materials(FGMs), a novel generation of microscopically composites in which the mechanical properties vary smoothly and continuously from one surface to another, proposed in the early 1980s [1, 2]. Structures made from these materials can effectively reduce thermal stress concentration so that they can be used in the high-temperature environments such as aerospace, optics, nuclear and civil engineering. So, the studies of the mechanical behaviors of FGM structures under the mechanical and thermal loadings have being attracted more and more attentions of scientists and also have become a new research field of solid mechanics.

Comprehensive studies on the vibration responses of FGM plates are available in the literatures, but most of which have been limited to analysis of beams and thin circular plates. For example, Xiang and Yang [3] carried out the free and forced vibration analysis of a laminated FGM Timoshenko beam with variable thickness under heat conduction. Li and Fan [4] proposed natural frequencies solutions for the free vibration of a FGM beam with a through-width delamination based on the Timoshenko beam theory. Leissa and Narita [5] investigated natural frequencies of a simply supported circular plate using Classical plate theory with ordinary and modified Bessel functions of the first kind. Kermani at al. [6] studied the free vibration analysis of multi-directional FGM circular and annular plates. Dong studied [7] three-dimensional free vibration of FGM annular plates based on Chebyshev-Ritz method. Wang at al. [8] investigated the axisymmetric free vibration of FGM thin circular plates based on the three-dimensional theory. Malekzadeh at al. [9] derived governing equations and boundary conditions by Hamilton principle of FGM circular arches with temperature-dependent properties in thermal environment and then gave the in-plane free vibration solutions. Iman at al. [10] provided an analytic solution for the free vibration of multi-directional FGM circular and annular plates. They used state-space differential quadrature method to find the semi-analytical or numerical solutions based on the three-dimensional theory of elasticity. Lee at al. [11] provided a semi-analytical solution for the free vibration analysis of circular plate with multiple holes by using the indirect boundary integral method. Ramesh and Mohan Rao [12] presented the natural frequencies of vibration of a rotating pre-twisted functionally graded cantilever beam. Ying et al. [13] presented solutions for bending and free vibration of FGM beams resting on a Winkler-Pasternak elastic foundation. By using classical beam theory, Aydogdu and Taskin [14] investigated the free vibration behavior of a simply supported FGM beam. Pradhan and Chakraverty [15] carried out the free vibration analysis of FGM thin elliptic plates with various edge supports.

Compared with the free vibration analysis of FGM beams and thin circular plates, the free vibration analysis of FGM thick plates is rare. Chen at al. [16] investigated the thermal behavior of a thick transversely isotropic FGM rectangular plate based on the three-dimensional elasticity theory. Kim and Lee [17] developed the geometrically nonlinear isogeometric analysis of FGM plates based on physical neutral surface and first-order shear deformation theory. Foroughi Hamid and Azhari Mojtaba [18] analyzed the mechanical buckling and free vibration of thick FGM plates resting on elastic foundation using the higher order B-spline finite strip method. Jha at al. [19] presented deformation and stress analyses of functionally graded thick plates based on the two-dimensional theory. Liu and Lee [20] provided a vibrations analysis of thick circular and annular plates based on three-dimensional theory with finite element method.

To the author’s best knowledge, in the previous works only the mechanical vibrations of FGM circular plates are investigated and there have been few researches dealing with the free vibration behavior of moderately thick circular plates, especially the effects of thermal environment are not considered. The few researches are Malekzadeh [21], who studied the free vibration characteristic of tapered Mindlin plates using DQM. Malekzadeh et al. [22] presented the vibration analysis of FGM thick annular plates subjected to thermal environment based on 3D elasticity theory. Considering the thermal environment effects and using Hamilton's principle, differential quadrature method is adopted to solve the equations of motion and the frequency parameters are obtained. Furthermore, Malekzadeh et al. [23] extended their work to the free vibration of FGM elastically supported FGM annular plates in thermal environment. Shen and Wang [24] reported a free vibration analysis of FGM rectangular plates resting on elastic foundations in thermal environments based on Voigt model and Mori-Tanaka model respectively.

Shooting method is found to be a simple and efficient numerical technique for solving non-linear governing equations. Some works have successfully used shooting method to analyze post-buckling, bending and vibration analysis. For example, Li and Zhou [25] carried out the non-linear vibration and thermal buckling of heated orthotropic circular plates by shooting method. Ma and Lee [26] investigated the nonlinear mechanical behaviors in-plane thermal loading of a beam made of FGM. Sun and Li [27] presented the thermal post-buckling of FGM circular plates subjected to transverse poing-space constraints, but they cannot consider the effect of thermal loading.

Therefore, in the present study, free vibration of a FGM moderately thick circular plate in thermal environment is presented by employing the numerical shooting technique. The material properties are thus assumed temperature-dependent and graded in the thickness direction. The equations of motion are derived using the Hamilton’s principle based on the first order shear deformation theory and three different boundary conditions are considered. After that, we employ the shooting method to solve the equations of motion with the related boundary conditions. The effects of uniform and non-uniform temperature rise parameters, gradients of materials properties, thickness ratio and boundary conditions on the natural frequencies are analyzed in detail.

2. Problem formulation

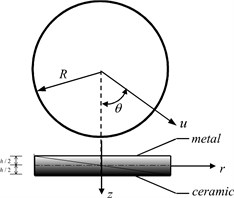
Consider a FGM moderately thick circular plate on Winkler foundation with radius $R$ and uniform thickness $h$ , which is made from a mixture of ceramic and metals. A cylindrical coordinate system $(r, θ, z)$ with its origin at the center of the mid-plane of the plate is defined, where $r$ , $θ$ and $z$ represent coordinates in the radial, circumferential and thickness directions, respectively. The coordinate system is illustrated in Fig. 1.

Fig. 1Geometry and coordinates of an FGM circular plate

2.1. Temperature field

Since functionally graded materials are most commonly used in high temperature environment, it is essential to take into consideration this temperature-dependency. Thus, the effective material properties $P$ of the metal and ceramic, such as elasticity modulus, $E,$ thermal expansion coefficient, $α$ , thermal conductivity, $K$ , Poisson’s ratio, $ν$ , may be expressed as a nonlinear function of temperature:

1

P = P_{0} (P_{- 1} T^{- 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3}) .

In which $T = T_{0} + Δ T$ and $T_{0} =$ 300 K (room temperature), the temperature-dependence coefficients $P_{- 1}$ , $P_{0}$ , $P_{1}$ , $P_{2}$ and $P_{3}$ are unique to the constituents.

In this section, we assume that the temperature variation is uniform or occurs in the thickness only. Therefore, the temperature distribution along the thickness direction can be obtained by solving a steady-state one-dimensional heat transfer equation:

2

- \frac{d}{d z} [K (z) \frac{d T}{d z}] = 0 .

This equation is solved by imposing boundary condition of $T (- \frac{h}{2}) = T_{m}$ , $T (\frac{h}{2}) = T_{c}$ :

3

T (z) = T_{m} + \frac{Δ T}{C} {\sum_{i = 0}^{\infty} (- 1)^{i} \frac{(K_{c} - K_{m})^{i}}{(i \times p + 1) {K_{m}}^{i}} (\frac{1}{2} + \frac{z}{h})}^{i \times p + 1} .

In which $Δ T = T_{c} - T_{m}$ , $C = \sum_{i = 0}^{\infty} (K_{c} - K_{m})^{i} / (i \times p + 1) {K_{m}}^{i}$ , where $K_{c}$ and $K_{m}$ denotes the ceramic and metal thermal conductivity.

2.2. Effective material properties of FGMs

According to Voigt rule, the effective material properties $P$ of FGMs may be written as:

4

P = P_{c} V_{c} + P_{m} V_{m},

where the subscripts $c$ and $m$ denote the ceramic and metallic constituents, respectively, $V_{c}$ and $V_{m}$ denotes the ceramic and metal volume fractions of and they can be expressed by $V_{c} + V_{m} = 1$ , the volume fraction $V_{c}$ defined a simple power low by:

5

V_{c} = {(\frac{1}{2} + \frac{z}{h})}^{p},

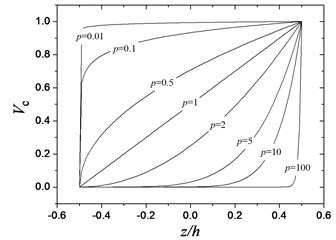
where $p$ is the gradient index of FGM. Fig. 2 shows the variations of volume fraction of ceramic phase through the thickness of plate for various values of $p$ calculated from Eq. (5).

Fig. 2Variations of the volume fraction of ceramic phase versus the dimensionless thickness of the FGM circular plate for different values of p

$Variations of the volume fraction of ceramic phase versus the dimensionless thickness of the FGM circular plate for different values of p$

For simplicity, the Poisson’s ratio $v$ is assumed to be a constant for functionally graded materials. The effective material properties follow the distribution law of Eqs. (4) and (5), namely:

6a

E (z, T) = E_{c} (T) {(\frac{1}{2} + \frac{z}{h})}^{p} + E_{m} (T) [1 - {(\frac{1}{2} + \frac{z}{h})}^{p}],

6b

α (z, T) = α_{c} (T) {(\frac{1}{2} + \frac{z}{h})}^{p} + α_{m} (T) [1 - {(\frac{1}{2} + \frac{z}{h})}^{p}],

6c

K (z, T) = K_{c} (T) {(\frac{1}{2} + \frac{z}{h})}^{p} + K_{m} (T) [1 - {(\frac{1}{2} + \frac{z}{h})}^{p}],

6d

ν (z) = ν,

6e

ρ (z) = ρ_{c} {(\frac{1}{2} + \frac{z}{h})}^{p} + ρ_{m} [1 - {(\frac{1}{2} + \frac{z}{h})}^{p}],

2.3. Governing equations

According to one-order shear plate theory, it can be assumed that the axisymmetric displacement field are:

7a

U_{r} (r, z, t) = z ψ (r, t),

7b

U_{θ} (r, z, t) = 0,

7c

U_{z} (r, z, t) = w (r, t) .

In which $U_{r}$ , $U_{θ}$ and $U_{z}$ are total displacement components along the coordinates $r$ , $θ$ and $z$ , respectively, $u$ and $w$ are the displacements in the mid-plane of the plate along the coordinates $r$ and $z$ , respectively, and $ψ$ denotes the slope at $z =$ 0 of the deformed line that was straight in the undeformed plate, $t$ is the time variable.

The strains can be expressed as follow:

8a

ε_{r} = \frac{\partial U_{r}}{\partial r},

8b

ε_{θ} = \frac{U_{r}}{r},

8c

γ_{r z} = \frac{\partial U_{r}}{\partial z} + \frac{\partial U_{z}}{\partial θ} .

Considering nonlinear strain-displacement relationships, one then obtains:

9a

ε_{r} = \frac{1}{2} {(\frac{\partial w}{\partial r})}^{2} + z \frac{\partial ψ}{\partial r},

9b

ε_{θ} = z \frac{ψ}{r},

9c

γ_{r z} = ψ + \frac{\partial w}{\partial r},

where $ε_{r}$ and $ε_{θ}$ are the normal strains and $γ_{r z}$ is the shear strain.

Based on Hooke’s law, the stress-strain relations are expressed by following formulations:

10

σ_{r} = \frac{E (z, T)}{1 - ν^{2}} (ε_{r} + ν ε_{θ}) - \frac{E (z, T) α (z, T)}{1 - ν} T (z),

11

σ_{θ} = \frac{E (z, T)}{1 - ν^{2}} (ε_{θ} + ν ε_{r}) - \frac{E (z, T) α (z, T)}{1 - ν} T (z),

12

τ_{r z} = \frac{E (z, T)}{2 (1 + ν)} γ_{r z} .

The stress can then be determined in terms of the mid-plane displacement through Eqs. (9a)-(9c), they can be calculated as:

13

σ_{r} = \frac{E (z, T)}{1 - ν^{2}} [\frac{1}{2} {(\frac{\partial w}{\partial r})}^{2} + z (\frac{\partial ψ}{\partial r} + ν \frac{ψ}{r})] - \frac{E (z, T) α (z, T)}{1 - ν} T (z),

14

σ_{θ} = \frac{E (z, T)}{1 - ν^{2}} [\frac{ν}{2} {(\frac{\partial w}{\partial r})}^{2} + z (\frac{ψ}{r} + ν \frac{\partial ψ}{\partial r})] - \frac{E (z, T) α (z, T)}{1 - ν} T (z),

15

τ_{r z} = \frac{E (z, T)}{2 (1 + ν)} (ψ + \frac{\partial w}{\partial r}) .

The membrane forces, the bending moments and the shear resultant force can be deduced from thickness integration of Eqs. (13), (14) and Eq. (15) respectively:

16a

N_{r} = \int_{- 0.5 h}^{0.5 h} σ_{r} d z = A_{11} \frac{1}{2} {(\frac{\partial w}{\partial r})}^{2} + B_{11} (\frac{\partial ψ}{\partial r} + ν \frac{ψ}{r}) - N_{T},

16b

N_{θ} = \int_{- 0.5 h}^{0.5 h} σ_{θ} d z = A_{11} \frac{ν}{2} {(\frac{\partial w}{\partial r})}^{2} + B_{11} (\frac{ψ}{r} + ν \frac{\partial ψ}{\partial r}) - N_{T},

16c

M_{r} = \int_{- 0.5 h}^{0.5 h} σ_{r} z d z = B_{11} \frac{1}{2} {(\frac{\partial w}{\partial r})}^{2} + D_{11} (\frac{\partial ψ}{\partial r} + ν \frac{ψ}{r}) - M_{T},

16d

M_{θ} = \int_{- 0.5 h}^{0.5 h} σ_{θ} z d z = B_{11} \frac{ν}{2} {(\frac{\partial w}{\partial r})}^{2} + D_{11} (\frac{ψ}{r} + ν \frac{\partial ψ}{\partial r}) - M_{T},

16e

Q_{r} = \int_{- 0.5 h}^{0.5 h} τ_{r z} d z = \frac{S}{κ_{s}} (ψ + \frac{\partial w}{\partial r}) .

Here $κ_{s}$ is the shear correction factor, for Mindlin plate $κ_{s} = 12 / π^{2}$ , Reissner plate $κ_{s} =$ 6/5. $A_{11}$ , $B_{11}$ , $D_{11}$ and $S$ are the stretching, bending-stretching coupling, bending and shear rigidity coefficient respectively; and the thermal membrane force $N_{T}$ and thermal bending moment $M_{T}$ can be calculated by following expressions:

17

(A_{11}, B_{11}, D_{11}) = \int_{- 0.5 h}^{0.5 h} \frac{E (z, T)}{1 - ν^{2}} (1, z, z^{2}) d z, S = \int_{- h / 2}^{h / 2} \frac{E (z)}{2 (1 + ν)} d z,

18

(N_{T}, M_{T}) = \int_{- 0.5 h}^{0.5 h} \frac{E (z, T) α (z, T)}{1 - ν} T (z) (1, z) d z .

Substitution of Eq. (6a) and Eq. (3) into Eq. (17) and Eq. (18) gives following statements:

(A_{11}, B_{11}, D_{11}) = \frac{E_{c} (T)}{1 - ν^{2}} (h f_{1}, h^{2} f_{2}, h^{3} f_{3}), S = \frac{E_{c} (T)}{2 (1 + ν)} h f_{1},

(N_{T}, M_{T}) = \frac{E_{c} (T) α_{c} (T)}{1 - ν} \int_{- 0.5 h}^{0.5 h} (T_{m} f_{4} + \frac{Δ T}{C} f_{5}) (1, z) d z .

Note that $E_{r} = E_{m} / E_{c},$ $α_{r} = α_{m} / α_{c},$ $K_{r} = K_{m} / K_{c}$ , $f_{i} (i = 1, 2, 3, 4, 5)$ are coefficients determined as follows:

f_{1} = E_{r} + \frac{1 - E_{r}}{p + 1},

f_{2} = \frac{p (1 - E_{r})}{2 (p + 1) (p + 2)},

f_{3} = \frac{E_{r}}{12} + \frac{(p^{2} + p + 2) (1 - E_{r})}{4 (p + 1) (p + 2) (p + 3)},

f_{4} = [E_{r} + (1 - E_{r}) {(\frac{1}{2} + \frac{z}{h})}^{p}] [α_{r} + (1 - α_{r}) {(\frac{1}{2} + \frac{z}{h})}^{p}],

f_{4} = [E_{r} + (1 - E_{r}) {(\frac{1}{2} + \frac{z}{h})}^{p}] [α_{r} + (1 - α_{r}) {(\frac{1}{2} + \frac{z}{h})}^{p}] \sum_{i = 0}^{\infty} {(- 1)}^{i} \frac{{(1 - K_{r})}^{i}}{(i \times p + 1) K_{r}^{i}} {(\frac{1}{2} + \frac{z}{h})}^{i \times p + 1}

2.4. Motion equations

The kinetic energy $T$ and the elastic potential $V_{e}$ of the FGM plate may be written as:

19

T = \frac{1}{2} \int_{Ω} ρ [{(\frac{\partial U_{r}}{\partial t})}^{2} + {(\frac{\partial U_{z}}{\partial t})}^{2}] d Ω,

20

V_{e} = \frac{1}{2} \int_{Ω} (σ_{r} ε_{r} + σ_{θ} ε_{θ} + τ_{r z} γ_{r z}) d Ω,

where $ρ = ρ (z, T)$ is the mass density of the FGM plate, and $Ω$ denotes domain of the FGM plate.

The load-displacement relationship of the foundation is assumed to be $q = k_{w} w - k_{g} \nabla^{2} w$ , where $q$ is the force per unit area, and $\nabla$ is Laplace differential operator; $k_{w}$ is the Winkler foundation stiffness and $k_{g}$ is a constant showing the effect of the shear interactions of the vertical elements.

The elastic foundation energy having shear deformable layers $V_{k}$ of the plate is expressed as follows:

21

V_{k} = \frac{1}{2} \iint_{A} [k_{w} w^{2} - k_{g} {(\frac{\partial w}{\partial r})}^{2}] d A .

2.5. Hamilton’s principle

The free vibration equations of motion will be derived according Hamilton’s principle, which has the following form:

22

δ Π = \int_{t_{1}}^{t_{2}} δ (T - V_{e} - V_{k}) d t,

where $t_{1}$ and $t_{2}$ are the beginning and end of motion time, respectively, in which the virtual kinetic energy is:

23

δ T = \iint_{A} I_{0} \frac{\partial w}{\partial t} δ \frac{\partial w}{\partial t} d A + \iint_{A} I_{2} \frac{\partial ψ}{\partial t} δ \frac{\partial ψ}{\partial t} d A .

The virtual elastic potential and elastic foundation energy may be expressed as follows:

24

δ V_{e} = \int_{Ω} (σ_{r} δ ε_{r} + σ_{θ} δ ε_{θ} + τ_{r z} δ γ_{r z}) d Ω = \iint_{A} (N_{r} \frac{\partial w}{\partial r} δ \frac{\partial w}{\partial r} + M_{r} δ \frac{\partial ψ}{\partial r} + \frac{M_{θ}}{r} δ ψ + Q_{r} δ ψ + Q_{r} δ \frac{\partial w}{\partial r}) d A .

25

δ V_{k} = \iint_{A} [k_{w} w δ w - k_{g} (\frac{1}{r} \frac{\partial w}{\partial r} + \frac{\partial^{2} w}{\partial r^{2}}) δ w] d A .

In which:

(I_{0}, I_{2}) = \int_{- \frac{h}{2}}^{\frac{h}{2}} ρ (z) (1, z^{2}) d z = ρ_{c} (h f_{6}, h^{3} f_{7}),

where:

f_{6} = ρ_{r} + \frac{1 - ρ_{r}}{p + 1}, f_{7} = \frac{ρ_{r}}{12} + \frac{(p^{2} + p + 2) (1 - ρ_{r})}{4 (p + 1) (p + 2) (p + 3)}, ρ_{r} = \frac{ρ_{m}}{ρ_{c}} .

Applying integrating by parts and collecting the coefficients of $δ ψ$ , $δ w$ , the governing equations of motion can be expressed as:

26a

δ ψ : \frac{\partial M_{r}}{\partial r} + \frac{M_{r} - M_{θ}}{r} - Q_{r} = I_{2} \frac{\partial^{2} ψ}{\partial t^{2}},

26b

δ w : \frac{\partial Q_{r}}{\partial r} + \frac{Q_{r}}{r} + \frac{1}{r} \frac{\partial}{\partial r} (r N_{r} \frac{\partial w}{\partial r}) - k_{w} w + k_{g} (\frac{\partial^{2} w}{\partial r^{2}} + \frac{1}{r} \frac{\partial w}{\partial r}) = I_{0} \frac{\partial^{2} w}{\partial t^{2}} .

Inserting Eqs. (16a)-(16e) into Eqs. (24a, b) and regardless of nonlinear terms, the governing equations of motion can be expressed as:

27a

D (\frac{\partial^{2} ψ}{\partial r^{2}} + \frac{1}{r} \frac{\partial ψ}{\partial r} - \frac{ψ}{r^{2}}) - \frac{S}{κ_{s}} (ψ + \frac{\partial w}{\partial r}) = I_{2} \frac{\partial^{2} ψ}{\partial t^{2}},

27b

\frac{S}{κ_{s}} (\frac{\partial ψ}{\partial r} + \frac{\partial^{2} w}{\partial r^{2}} + \frac{ψ}{r} + \frac{1}{r} \frac{\partial w}{\partial r}) - N_{T} (\frac{\partial^{2} w}{\partial r^{2}} + \frac{1}{r} \frac{\partial w}{\partial r}) - k_{w} w + k_{g} (\frac{\partial^{2} w}{\partial r^{2}} + \frac{1}{r} \frac{\partial w}{\partial r}) = I_{0} \frac{\partial^{2} w}{\partial t^{2}} .

Assume that the vibration of circular plate is harmonic. Then, the dynamic response can be expressed as:

28a

w (r, t) = \tilde{w} (r) c o s Ω t,

28b

ψ (r, t) = \tilde{ψ} (r) c o s Ω t,

where $Ω$ is the natural frequency, and $\tilde{w} (r)$ and $\tilde{ψ} (r)$ are the shape functions. Substituting Eqs. (28a) and (28b) into Eqs. (27a) and (27b) gives the governing equations of motion of the problem as follow:

29a

D (\frac{d^{2} \tilde{ψ}}{d r^{2}} + \frac{1}{r} \frac{d \tilde{ψ}}{d r} - \frac{\tilde{ψ}}{r^{2}}) - \frac{S}{κ_{s}} (\tilde{ψ} + \frac{d \tilde{w}}{d r}) = - I_{2} \tilde{ψ} Ω^{2},

29b

\frac{S}{κ_{s}} (\frac{d \tilde{ψ}}{d r} + \frac{d^{2} \tilde{w}}{d r^{2}} + \frac{\tilde{ψ}}{r} + \frac{1}{r} \frac{d \tilde{w}}{d r}) - N_{T} (\frac{d^{2} \tilde{w}}{d r^{2}} + \frac{1}{r} \frac{d \tilde{w}}{d r}) - k_{w} \tilde{w} + k_{g} (\frac{d^{2} \tilde{w}}{d r^{2}} + \frac{1}{r} \frac{d \tilde{w}}{d r}) = - I_{0} \tilde{w} Ω^{2} .

Non-dimensional variables are introduced as follows:

ξ = \frac{r}{R}, W = \frac{\tilde{w}}{R}, δ = \frac{h}{R}, K w = \frac{12 (1 - ν^{2}) k_{w} R^{4}}{E_{c} h^{3}}, K g = \frac{12 (1 - ν^{2}) k_{g} R^{2}}{E_{c} h^{3}},

ω_{n} = Ω R^{2} \sqrt{\frac{12 (1 - ν^{2}) ρ_{c} h}{E_{c} h^{3}}} .

Substitution of the above non-dimensional transformation into Eqs. (29a) and (29b) gives the governing equations of the FGM Reissner-Mindlin circular plates in dimensionless forms as:

30

12 δ^{2} f_{3} (\frac{d^{2} \tilde{ψ}}{d ξ^{2}} + \frac{1}{ξ} \frac{d \tilde{ψ}}{d ξ} - \frac{\tilde{ψ}}{ξ^{2}}) - \frac{6 (1 - ν)}{κ_{s}} f_{1} (\tilde{ψ} + \frac{d W}{d ξ}) = - δ^{4} f_{7} \tilde{ψ} ω_{n}^{2},

31

\frac{6 (1 - ν)}{κ} f_{1} (\frac{d^{2} W}{d ξ^{2}} + \frac{1}{ξ} \frac{d W}{d ξ} + \frac{d \tilde{ψ}}{d ξ} + \frac{\tilde{ψ}}{ξ}) - δ^{2} K_{w} W + (δ^{2} K_{g} - {N^{'}}_{T}) (\frac{d^{2} W}{d ξ^{2}} + \frac{1}{ξ} \frac{d W}{d ξ}) = - δ^{2} f_{6} W ω_{n}^{2} .

In which:

{N'}_{T} = 12 (1 + ν) α_{c} (T_{m} \int_{0}^{1} g_{1} d t + \frac{Δ T}{C} \int_{0}^{1} g_{2} d t),

where:

g_{1} = [E_{r} + (1 - E_{r}) t^{p}] [α_{r} + (1 - α_{r}) t^{p}],

g_{2} = [E_{r} + (1 - E_{r}) t^{p}] [α_{r} + (1 - α_{r}) t^{p}] \sum_{i = 0}^{\infty} (- 1)^{i} \frac{(1 - K_{r})^{i}}{(i \times p + 1) {K_{r}}^{i}} t^{i \times p + 1} .

In the present study, three traditional boundary conditions are considered. Boundary conditions in dimensions form can be written as:

32

\tilde{ψ} = 0, \frac{d W}{d ξ} + \tilde{ψ} = 0, ξ = 0 .

Clamped edge (C):

33

\tilde{ψ} = 0, W = 0, ξ = 1 .

Simply supported edge (S):

34

\frac{d \tilde{ψ}}{d ξ} + ν \tilde{ψ} = 0, W = 0, ξ = 1 .

Free edge (F):

35

\frac{d \tilde{ψ}}{d ξ} + ν \tilde{ψ} = 0, \frac{d W}{d ξ} + \tilde{ψ} = 0, ξ = 1 .

3. Shooting method

Due to complexity and the coupling of these partial differential equations, it is very different to obtain any analytical solution of this problem. In what follows, a shooting method [25-27] is employed to numerically solve the problems. Here, the governing Eqs. (30) and (31) and boundary conditions Eqs. (32)-(33), (32)-(34) and (32)-(35) can be rewritten in the standard form:

36a

\frac{d Y}{d ξ} = H (ξ, Y), (0 < ξ < 1),

36b

B_{0} Y (0) = b_{0},

36c

B_{1} Y (1) = b_{1},

where:

Y = {[y_{1}, y_{2}, y_{3}, y_{4}, y_{5}]}^{T} = {[\tilde{ψ}, \frac{d \tilde{ψ}}{d ξ}, W, \frac{d W}{d ξ}, ω_{n}]}^{T},

H = {[y_{2}, Δ_{1}, y_{4}, Δ_{2}, 0]}^{T} .

Expressions of $Δ_{1}$ , $Δ_{2}$ and $b_{1}$ , $b_{2}$ are as follows:

Δ_{1} = \frac{y_{1}}{ξ^{2}} - \frac{y_{2}}{ξ} + \frac{(1 - ν)}{2 δ^{2} κ_{s}} \frac{f_{1}}{f_{_{3}}} (y_{1} + y_{4}) - \frac{δ^{2}}{12} \frac{f_{7}}{f_{3}} y_{1} {y_{5}}^{2},

Δ_{2} = \frac{[- \frac{6 (1 - ν)}{κ} f_{1} (\frac{y_{4}}{ξ} + \frac{y_{1}}{ξ} + y_{2}) + ({N'}_{T} - δ^{2} K_{g}) \frac{y_{4}}{ξ} + δ^{2} K_{w} y_{3} - δ^{2} f_{6} y_{3} {y_{5}}^{2}]}{[\frac{6 (1 - ν)}{κ} f_{1} + (δ^{2} K_{g} - N_{T}^{'})]},

b_{0} = {\{\begin{array}{l} 0 & η & 0 \end{array}\}}^{T}, b_{1} = {\{\begin{array}{l} 0 & 0 \end{array}\}}^{T},

where $η$ is a dimensionless deflection parameter.

$B_{0}$ and $B_{1}$ are matrixes of order 3×5 and 2×5 respectively, they are:

B_{0} = [\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}] .

For the clamped boundary:

B_{1} = [\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}] .

For the Simply supported boundary:

B_{1} = [\begin{array}{l} ν & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}] .

For the free boundary:

B_{1} = [\begin{array}{l} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}] .

Consider the initial value problem:

37a

\frac{d G}{d ξ} = H (ξ, G),

37b

G (0) = I (η, D),

where $G = {\{g_{1}, g_{2}, g_{3}, g_{4}, g_{5}\}}^{T}$ , $I = {\{0, d_{1}, η, 0, d_{2}\}}^{T}$ , and $D = {\{d_{1}, d_{2}\}}^{T}$ is the initial parameter vector.

The unique solution for the initial value problem must exist, namely:

38

G (ξ; η, D) = I (η, D) + \int_{0}^{ξ} H (ζ, G) d ζ .

For given value of $η$ , we seek components of $D^{*} = {\{d_{1}^{*}, d_{2}^{*}\}}^{T}$ such that a solution of Eq. (38) satisfies boundary condition Eq. (37b), that is:

39

B_{1} G (ξ; η, D^{*}) = {\{0 ， 0\}}^{T} .

Obviously, if $D = D^{*}$ is a root of Eq. (39), the solution of the boundary-value problem Eq. (36) is then obtained as:

40

Y (ξ) = G (ξ; η, D^{*}) .

We employ the Runge-Kutta method to integrate the system Eq. (38) of ordinary differential equations, and the Newton-Raphson iteration method to search for a root $D^{*}$ of Eq. (39) to find a numerical solution of the boundary-value problem Eq. (36). This approach is called a shooting method.

4. Shooting method for approximate solutions of free vibration of FGM Reissner-Mindlin plates

In what follows, the material properties of ceramic, $Z r O_{2}$ , and metallic, Ti-6Al-4V, as given in Table 1, are used in the numerical computations.

4.1. Comparison studies

To ensure the accuracy and effectiveness of shooting method, two examples are solved for free vibration of homogeneous and FGM Mindlin circular plate.

Table 1Temperature-dependent coefficients for ceramic and metals from Reddy and Chin [28]

Material	Proprieties	$P_{- 1}$	$P_{0}$	$P_{1}$	$P_{2}$	$P_{3}$
Ti-6Al-4V	$E$ (GPa)	0	122.7e+9	–4.605e-4	–4.605-4	0
$Z r O_{2}$	$α$ (1/K)	0	7.5788e-6	6.638e-4	–3.147e-6	0
	$κ$ (W/mK)	0	1.0	1.704e-2	0	0
	$ρ$ (kg·m^-3)	0	4229	0	0	0
	$E$ (GPa)	0	244.27e+9	–1.371e-3	1.214e-6	–3.681e-10
	$α$ (1/K)	0	12.766e-6	–1.491e-3	1.006e-5	0
	$κ$ (W/m K)	0	1.7	1.276e-4	6.648e-8	0
	$ρ$ (kg·m^-3)	0	3000	0	0	0

Example 1. When the power law index $p$ equals zero, the functionally graded material is reduced to the homogeneous ceramics Mindlin circular plate. In order to show the accuracy of the present numerical method, by giving $p =$ 0, $ν =$ 0.3, $K_{w} = K_{g} =$ 0, $δ =$ 0.2，the comprehensive comparison between the shooting method results and those in Ref. [29] is given in Table 2, which includes the cases of above-mentioned three sets of boundary conditions. Obviously, the first four lower-order dimensionless natural frequencies show good agreement with the existing results.

Example 2. The first three order dimensionless fundamental frequency parameters $ω$ of the FGM thick circular plates for the three traditional boundary conditions are calculated and compared in Table 3 with a set of results [15] based on Rayleigh-Ritz method. The present results are in good agreement with existing results.

Tables 2-3 show that the present results agree well existing results, and thus the accuracy of the shooting method technique are confirmed.

Table 2The first fourth dimensionless natural frequencies ωn for thick circular plates under three sets of boundary conditions

Boundary condition		$ω_{1}$	$ω_{2}$	$ω_{3}$	$ω_{4}$
$C$	Present	9.2401	30.211	56.683	85.572
$C$	[29]	9.2400	30.211	56.682	85.571
$S$	Present	4.7773	24.995	52.514	82.767
$S$	[29]	4.7777	24.994	52.514	82.766
$F$	Present	–	8.5051	31.111	59.646
$F$	[29]	–	8.5050	31.111	59.645

Table 3Dimensionless natural frequencies ωn of FGM Mindlin plates with different graded index δ= 0.01

Boundary condition			$ω_{n}$
Boundary condition			$p =$ 0.0	$p =$ 0.1	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
$C$	1	Present	10.213	9.9836	9.4503	9.1331	8.815	8.591
		[15]	10.216	9.8510	8.973	8.500	8.125	7.576
	2	Present	39.734	38.843	36.767	35.532	33.423	33.423
		[15]	39.773	38.352	34.933	33.093	29.496	29.496
$S$	1	Present	4.935	4.823	4.5673	4.4133	4.2684	4.1426
		[15]	4.935	4.759	4.335	4.106	3.925	3.659
	2	Present	29.704	29.036	27.486	26.564	25.416	24.667
		[15]	29.736	28.674	26.118	24.742	23.651	22.052
$F$	2	Present	8.9686	8.7673	8.2986	8.0204	7.7737	5.9883
		[15]	9.003	8.682	7.908	7.491	7.161	6.677
	3	Present	37.787	36.939	34.964	33.793	32.754	25.2045
		[15]	37.564	36.221	32.993	31.225	29.877	27.857

4.2. Numerical results and discussions

In this section, the free vibration of a FGM thick circular plate is numerically analyzed in thermal environment. Table 4 shows the first three order dimensionless fundamental frequency parameters $ω$ of the FGM thick circular plates for clamped boundary condition changing with the power law index $p$ in room temperature fields without elastic foundation. It can be seen that all the frequencies decrease with the increasing of power law index $p$ , which is due to the fact that the decrease of rigidity of the plate, or the increase of the component of metallic in the plate. Also, along with the increase in the value of $δ$ , the frequencies decrease.

Table 4Dimensionless natural frequencies ωn of FGM thick circular plates with clamped edge (ν= 0.3, Tc=Tm= 300 K, Kw=Kg= 0)

$δ$		$ω$
		Mindlin solution						Reissner solution
		$p =$ 0.0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	1	8.6948	7.9758	7.3639	6.8684	6.4509	6.0217	8.7051	7.9850	7.3724	6.8763	6.4587	6.0291
	2	29.464	27.028	24.908	23.111	21.529	19.931	29.538	27.095	24.969	23.168	21.585	19.983
	3	55.752	51.185	47.158	43.659	40.514	37.355	55.944	51.358	47.317	43.808	40.655	37.488
0.3	1	8.1034	7.3952	6.8503	6.3628	5.9388	5.5085	8.1201	7.4468	6.8642	6.3759	5.9514	5.5206
	2	24.245	22.211	20.516	18.984	17.599	16.213	24.333	22.347	20.589	19.053	17.665	16.274
	3	43.037	39.484	36.446	33.674	31.129	28.594	43.226	39.731	36.604	33.822	31.267	28.723

Subjected to room temperature or heat conduction, the fundamental frequencies decrease significantly with increasing the value of $δ$ in Fig. 3 and 4. It can be found that for a giving $δ$ , Ceramic plate provide the largest fundamental frequency while the metal plate hold the smallest one. Table 5 shows the effect of uniform temperature rise on the first three-order dimensionless frequency parameters for FGM Mindlin plate with $δ =$ 0.2 and clamped ends that frequencies monotonously decrease as uniform temperature rise increase.

Fig. 3Fundamental dimensionless frequency parameter ω1 of clamped plate versus δ in room temperature field

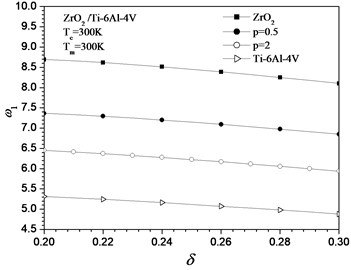
Fig. 4Fundamental dimensionless frequency parameter ω1 of clamped plate versus δ subjected to heat conduction

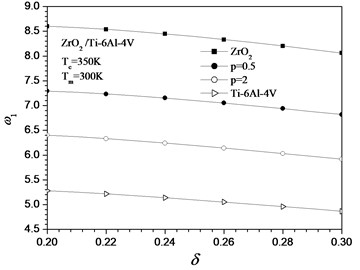
Table 5Dimensionless natural frequencies ωn of FGM thick circular plates with clamped edge (ν= 0.3, δ= 0.2, Kw=Kg= 0)

$δ$	$ω$
	$T_{c} = T_{m} =$ 400 K						$T_{c} = T_{m} =$ 500 K
	$p =$ 0.0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
1	8.5046	7.8108	7.2219	6.7486	6.3529	5.9435	8.3095	7.6418	7.0768	6.6245	6.2531	5.8641
2	29.211	26.808	24.719	22.950	21.397	19.823	28.956	26.588	24.528	22.788	21.263	19.715
3	55.439	50.914	46.924	43.460	40.347	37.219	55.124	50.642	46.689	43.259	40.180	37.084

In order to compare uniform and non-uniform temperature rise effects, average temperature of non-uniform parameters equal to the temperature of uniform case are considered. Table 6 shows the effect of uniform temperature rise and heat conduction on the free vibration of FGM Mindlin circular plates without elastic foundation. It can be observed that for the same value of both uniform and non-uniform rise, the first-three frequency parameters of FGM Mindlin plate decrease with increasing the power law index $p$ . One can see that the frequency in case of uniform heating is smaller than that of the non-uniform temperature rise.

Table 6Fundamental dimensionless frequencies ω1 of FGM thick circular plates with clamped edge subject to temperature rise and heat conduction (ν= 0.3, δ= 0.2, Kw=Kg= 0)

	$ω$
	$p =$ 0	$p =$ 0.1	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 100
$T_{c} = T_{m} =$ 325 K	8.6484	8.4774	8.0844	7.8528	7.6488	7.4601	7.2487
$T_{c} = T_{m} =$ 350 K	8.6008	8.4334	8.0468	7.8198	7.6210	7.4355	7.2278
$T_{c} = T_{m} =$ 375 K	8.5528	8.3881	8.0091	7.7875	7.5922	7.4117	7.2069
$T_{c} =$ 350 K, $T_{m} =$ 300 K	8.6873	8.5146	8.1137	7.8788	7.6715	7.4789	7.2664
$T_{c} =$ 400 K, $T_{m} =$ 300 K	8.6797	8.5063	8.1067	7.8719	7.6648	7.4740	7.2632
$T_{c} =$ 450 K, $T_{m} =$ 300 K	8.6437	8.4988	8.0996	7.8650	7.6589	7.4691	7.2592

The effects of two-parameter elastic foundation on the first-three frequency parameters of the FGM thick circular plates in thermal environment are exhibited in Table 7. As we expect, the elastic foundation has significant effects on the first-three frequencies of FGM Mindlin plates subjected to uniform temperature and heat conduction, the results are bigger than the frequencies without elastic foundation. Obviously, additional elastic foundation leads frequency rise due to the decrease of the flexibility and the deformation capacity.

Table 7Dimensionless natural frequencies ωn of FGM thick circular plates with clamped edge (ν= 0.3, Kw= 50, Kg= 5)

$δ$		$ω$
		$T_{c} = T_{m} =$ 325 K						$T_{c} =$ 350 K, $T_{m} =$ 300 K
		$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	1	12.509	11.772	11.141	10.630	10.155	9.7098	12.524	11.784	11.149	10.618	10.161	9.7499
	2	32.575	30.159	28.065	26.322	24.729	23.177	32.603	30.180	28.081	26.299	24.739	23.256
	3	59.129	54.584	50.595	47.184	44.047	40.973	59.165	54.612	50.615	47.154	44.061	41.079
0.3	1	10.214	9.5429	8.9591	8.4667	8.0138	7.5773	10.221	9.5485	8.9631	8.4609	8.0163	7.5963
	2	27.813	25.843	24.112	22.624	21.259	19.937	27.827	25.854	24.119	22.613	21.265	19.977
	3	47.875	44.399	41.319	38.630	36.150	33.742	47.894	44.414	41.330	38.614	36.157	33.798

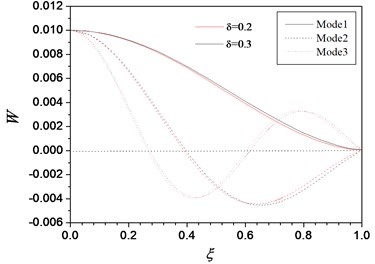
Figs. 5 shows the anterior three-order modes of vibration for a FGM thick circular plate with clamped edge. It can be seen that the first three order mode diagrams with $δ =$ 0.2 are very close to the one with $δ =$ 0.3. Also, the mode diagrams are in good agreement with the boundary conditions.

Fig. 5Anterior third-order modes of FGM moderately thick circular plate with clamped edge

Consider a FGM Mindlin circular plate with and without elastic foundation which is simply supported or free edge. Table 8 shows the effect of uniform temperature rise and heat conduction on the free vibration of FGM Mindlin circular plates with simply supported edge without elastic foundation. It can be found that for the same value of both uniform and non-uniform rises, the first-three frequency parameters of FGM Mindlin plate are decreased by increasing the power law index $p$ . Subjected to the same temperature loads, the first-three frequency parameters decrease with increasing the ratio of the thickness to the radius in Table 4 and 7, but it is not always true for the FGM moderately thick circular plates with simply supported edge due to effect of heat conduction in Table 8. Also, the influence of two-parameter elastic foundation on the first-three frequencies of FGM circular plates in room and uniform temperature rise is exhibited in Table 9. As we expect, the elastic foundation has significant effects on the first-three frequencies of FGM Mindlin plates subjected to uniform temperature and heat conduction, the results are bigger than the frequencies without elastic foundation. Subjected to room temperature, uniform temperature rises and heat conduction, the second and third-order frequencies for FGM moderately thick circular plates with free edge are calculated (see Tables 10-11). It also can be found that the frequency in case of uniform heating is smaller than that of the non-uniform temperature rise. Also, one can see that increasing the thickness of the circular plate, the first-three frequency parameters decrease.

Table 8Dimensionless natural frequencies ωn of FGM thick circular plates with simply supported edge (Kw=Kg= 0)

$δ$		$ω$
		$T_{c} = T_{m} =$ 325 K						$T_{c} =$ 350 K, $T_{m} =$ 300 K
		$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	1	3.6883	3.4191	3.2044	3.0511	2.9396	2.8112	3.7344	3.4556	3.2311	3.0718	3.9562	2.8257
	2	24.046	22.038	20.323	18.909	17.703	16.467	24.082	22.066	20.344	18.926	17.717	16.479
	3	51.437	47.174	43.468	40.312	37.526	34.705	51.478	47.206	43.492	40.331	37.542	34.719
0.25	1	4.0256	3.7072	3.4449	3.2441	3.0857	2.9158	4.0525	3.7286	3.4607	3.2564	3.0957	2.9246
	2	22.613	20.728	19.105	17.746	16.568	15.368	22.638	20.747	19.119	17.758	16.578	15.377
	3	46.006	42.222	38.901	36.027	33.451	30.856	56.035	42.245	38.918	36.040	33.462	30.866
0.3		4.1439	3.8063	3.5247	3.3033	3.1234	2.9345	4.1619	3.8207	3.5354	3.3116	3.1302	2.9406
		21.119	19.365	17.844	16.556	15.423	14.275	21.137	19.379	17.855	16.564	15.430	14.281
		41.296	37.925	34.941	32.325	29.951	27.572	41.318	37.943	34.955	32.335	29.960	27.580

Table 9Dimensionless natural frequencies ωn of FGM thick circular plates with simply supported edge (Kw= 50, Kg= 5)

$δ$		$ω$
		$T_{c} = T_{m} =$ 325 K						$T_{c} =$ 350 K, $T_{m} =$ 350 K
		$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	1	9.5876	9.1729	8.7978	8.5058	8.2371	7.9820	9.4763	9.0761	8.7311	8.4373	8.1825	7.9404
	2	27.798	25.792	24.051	22.663	21.450	20.238	27.601	25.618	23.929	22.534	21.344	20.155
	3	55.194	50.936	47.210	44.113	41.359	38.603	54.960	50.725	47.060	43.953	41.226	38.498

Table 10Dimensionless natural frequencies ωn of FGM thick circular plates with free edge (ν=0.3, Kw=Kg= 0)

$δ$		$ω$
		$T_{c} =$ 300 K, $T_{m} =$ 300 K						$T_{c} =$ 400 K, $T_{m} =$ 400 K
		$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	2	8.0032	7.3311	6.7677	6.3221	5.9564	5.5768	7.8281	7.1795	6.6373	6.2119	5.8657	5.5042
0.2	3	30.343	27.779	25.596	23.800	22.264	20.689	30.082	27.555	25.402	23.635	22.126	20.578
0.25	2	7.9352	7.2618	6.6958	6.2437	5.8689	5.4817	7.8210	7.1629	6.6107	6.1715	5.8092	5.4335
0.25	3	28.075	25.707	23.681	21.995	20.536	19.044	27.895	25.552	23.547	21.881	20.440	18.966
0.3	2	7.7676	7.1050	6.5474	6.0994	5.7257	5.3399	7.6855	7.0340	6.4862	6.0473	5.6824	5.3048
0.3	3	25.879	23.702	21.832	20.262	18.889	17.488	25.745	23.586	21.732	20.176	18.817	17.429

Table 11Dimensionless natural frequencies ωn of FGM thick circular plates with free edge (ν= 0.3, Tc= 300 K, Tm= 400 K, Kw=Kg= 0)

$δ$		$ω$
		Mindlin solution						Reissner solution
		$p =$ 0.0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5	$p =$ 0	$p =$ 0.2	$p =$ 0.5	$p =$ 1	$p =$ 2	$p =$ 5
0.2	2	7.8281	7.1795	6.6373	6.2119	5.8657	5.5042	7.8321	7.1831	6.6405	6.2149	5.8685	5.5069
0.2	3	30.082	27.555	25.402	23.635	22.126	20.578	30.131	27.598	25.442	23.672	22.163	20.613
0.25	2	7.8210	7.1629	6.6107	6.1715	5.8092	5.4335	7.8262	7.1675	6.6148	6.1753	5.8129	5.4370
0.25	3	27.895	25.552	23.547	21.881	20.440	18.966	27.952	25.604	23.594	21.925	20.483	19.007
0.3	2	7.6855	7.0340	6.4862	6.0473	5.6824	5.3048	7.6917	7.0395	6.4912	6.0519	5.6869	5.3092
0.3	3	25.745	23.586	21.732	20.176	18.817	17.429	25.679	23.643	21.832	20.225	18.864	17.475

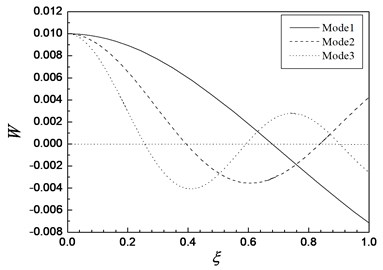
Figs. 7 and 8 show the anterior three-order modes of vibration for FGM circular plates with simply supported and free edge. Also, the mode diagrams are in good agreement with the boundary conditions.

Fig. 7Anterior third-order modes of FGM moderately thick circular plate with simply supported edge

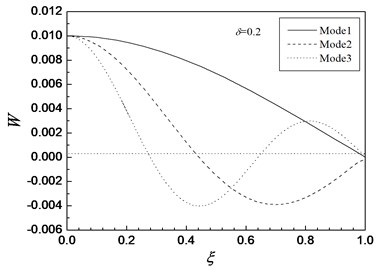
Fig. 8Anterior third-order modes of the FGM moderately thick circular plate free edge

5. Conclusions

In this paper, the free vibration of functionally graded moderately thick circular plates resting on two-parameter elastic foundations in thermal environment has been presented by employing the numerical shooting technique. Investigations on vibration of FGM thick circular plates in thermal environment with three different boundaries are also introduced. Material primary parameters are assumed temperature-dependent and vary along the thickness of the plate. By employing a shooting method, the non-linear governing equations are solved numerically and the natural frequencies of the circular plates are obtained. The effects of uniform temperature rise and heat conduction, material constant, boundary conditions and elastic foundations on the natural frequency parameters are discussed in detail. Looking into the present results, one may conclude as follows.

1) The natural frequency parameters of vibration are decreases with increasing the ratio of the thickness to the radius for both the homogeneous ceramics plate and FGM plate without thermal environment, but it is not always true for a FGM plate with simply supported edge due to effect of heat conduction. The uniform temperature rise has more effect than the non-uniform temperature rises on the frequency parameters.

2) All the first-three order frequencies of the FGM moderately thick circular plates in thermal environment decrease monotonously with the increase of the value of $p$ , the reason is that the increase of the volume fraction of the metal reduces the bending stiffness of the whole plate.

3) The effect of elastic foundation on the free vibration is significant. The natural frequency of vibration for the plate is lower than the plates with elastic foundation. Also, the boundary conditions have large influence on vibration frequency of the thick plates. The natural frequency parameters are maximum with fixed boundary condition but it is minimum under free boundary condition.

4) The solutions can be used as benchmark for other numerical methods.

References

Yamanouchi M., Hirai T., Shiota I., et al. Proceeding of the First International Symposium on Functionally Gradient Materials, Sendai Japan, 1990.

Search CrossRef
Koizumi M. The concept of FGM. Ceramic Transactions Functionally Gradient Materials, Vol. 34, 1993, p. 3-10.

Search CrossRef
Xiang H. J., Yang J. Free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Composites, Part B: Engineering, Vol. 39, 2008, p. 292-303.

Publisher
Li S. R., Fan L. L. Free vibration of FGM Timoshenko beams with through-width delamination. Science China Physics, Mechanics and Astronomy, Vol. 57, 2014, p. 927-934.

Publisher
Leissa A. W., Narita. Y. Natural frequencies of simply supported circular plates. Journal of Sound and Vibration, Vol. 70, 1990, p. 221-229.

Publisher
Kermani I. D., Ghayour M., Mirdamadi H. R. Free vibration analysis of multi-directional functionally graded circular and annular plates. Journal of Mechanical and Technology, Vol. 26, 2012, p. 3399-3410.

Search CrossRef
Dong C.Y. Three-dimensional free vibration analysis of functionally graded annular plates using the Chebyshev-Ritz method. Materials and Design, Vol. 29, 2008, p. 1518-1525.

Publisher
Wang Y., Xu R. Q., Ding H. J. Free axisymmetric vibration of FGM circular plates. Applied Mathematics and Mechanics (English Edition), Vol. 30, 2009, p. 1077-1082.

Publisher
Malekzadeh P., Atashi M. M., Karami G. In-plane free vibration of functionally graded circular arches with temperature-dependent properties under thermal environment. Sound and Vibration, Vol. 326, 2009, p. 837-851.

Publisher
Iman D.K., Mostafa G., Hamid R. M. Free vibration analysis of multi-directional functionally graded circular and annular plates. Journal of Mechanical Science and Technology, Vol. 26, 2012, p. 3399-3410.

Publisher
Lee W. M., Chen J. T., Lee Y. T. Free vibration analysis of circular plates with multiple circular holes using indirect BIEMs. Journal of Sound and Vibration, Vol. 304, 2007, p. 811-830.

Publisher
Ramesh M. N. V., Mohan Rao N. Free vibration analysis of pre-twisted rotating FGM beams. International Journal of Mechanics and Materials in Design, Vol. 9, 2013, p. 367-383.

Publisher
Ying J., Lu C. F., Chen W. Q. Two-dimensional elasticity solutions for functionally graded beams resting on elastic foundations. Composite Structure, Vol. 84, 2008, p. 209-219.

Publisher
Aydogdu M., Taskin V. Free vibration analysis of functionally graded beams with simply supported edges. Materials Design, Vol. 28, 2007, p. 1651-1656.

Publisher
Pradhan K. K., Chakraverty S. Free vibration of functionally graded thin elliptic plates with various edge supports. Structural Engineering and Mechanics, Vol. 53, Issue 2, 2015, p. 337-354.

Publisher
Chen W. Q., Bian Z. G., Ding H. J. Three-dimensional analysis of a thick FGM rectangular plate in thermal environment. Journal of Zhejiang University, Science A, Vol. 4, 2003, p. 1-4.

Publisher
Kim N-Il., Lee J. H. Geometrically nonlinear isogeometric analysis of functionally graded plates based on first-order shear deformation theory considering physical neutral surface. Composite Structures, Vol. 153, 2016, p. 804-814.

Publisher
Foroughi H., Azhari M. Mechanical buckling and free vibration of thick functionally graded plates resting on elastic foundation using the higher order B-spline finite strip method. Meccanica, Vol. 49, 2014, p. 981-993.

Publisher
Jha D. K., Kant T., Singh R. K. An accurate two-dimensional theory for deformation and stress analyses of functionally graded thick plates. International of Advance Structure Engineering, Vol. 62, 2014, p. 1-11.

Publisher
Liu Z., Lee Y. T. Finite element analysis of three-dimensional vibrations of thick circular and annular plates. Journal of Sound and Vibration, Vol. 233, Issue 1, 2000, p. 63-80.

Publisher
Malekzadeh P. Nonlinear free vibration of tapered Mindlin plates with edges elastically restrained against rotation using DQM. Thin-Walled Structure, Vol. 46, 2008, p. 11-26.

Publisher
Malekzadeh P., Shahpari S. A. Ziaee H. R. Three-dimensional free vibration off thick functionally graded annular plates in thermal environment. Journal of Sound and Vibration, Vol. 329, 2010, p. 425-442.

Publisher
Malekzadeh P., Golbahar Haghighi M. R., Atashi M. M. Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment. Meccanica, Vol. 46, 2011, p. 893-913.

Publisher
Shen H. S., Wang Z. X. Assessment of Voigt and Mori-Tanaka models for vibration analysis of functionally graded plates. Composite Structures, Vol. 94, 2012, p. 2197-2208.

Publisher
Li S. R., Zhou Y. H. Shooting method for non-linear vibration and thermal buckling of heated orthotropic circular plates. Journal of Sound and Vibration, Vol. 248, 2001, p. 379-386.

Publisher
Ma L. S., Lee D. W. A further discussion of nonlinear mechanical behavior for FGM beams under in-plane thermal loading. Composite Structures, Vol. 93, 2011, p. 831-842.

Publisher
Yun S., Li S. R. Thermal post-buckling of functionally graded material circular plates subjected to transverse point-space constraints. Journal of Thermal Stresses, Vol. 37, 2014, p. 1153-1172.

Publisher
Reddy J. N., Chin C. D. Theromechanical analysis functionally graded cylinders and plates. Journal of Thermal Stresses, Vol. 21, 1998, p. 593-626.

Publisher
Irie T., Yamada G., Takagi K. Natural frequencies of thick annular plates. Journal of Applied of Mechanics, Vol. 49, Issue 3, 1982, p. 633-638.

Publisher

Cited by

The influence of surface effects on axisymmetric vibration of graded porous Mindlin circular nanoplate in a temperature field

Qinglu Li | Haikun Zhang | Siyao Wang | Jinghua Zhang

(2024)

Nonlinear post-buckling of graded porous circular nanoplate with surface stress subjected to follower force

Qinglu Li | Xuanhe Zhao | Zhaoyi Pan | Jinghua Zhang

(2024)

Axisymmetric thermal vibration analysis of graded porous circular plates based on physical neutral surface and Reddy’s third-order shear theory

Qinglu Li | Haikun Zhang | Siyao Wang

(2024)

Free vibration analysis of graded porous circular micro/nanoplates with various boundary conditions based on the nonlocal elasticity theory

Qinglu Li | Siyao Wang | Jinghua Zhang

(2023)

Thermal vibration analysis of functionally graded circular plates based on Levinson’s third-order shear deformation theory

Yu Chen | Qing-Lu Li

(2023)

Nonlinear vibration analysis of elastically supported multi-layer composite plates using efficient quadrature techniques

Ola Ragb | M. S. Matbuly

(2022)

Axisymmetric vibration analysis of graded porous Mindlin circular plates subjected to thermal environment

Qing-Lu Li | Xin Yan | Jing-Hua Zhang

(2021)

Numerical Methods in Calculating Eigenvalues: Case Studies in Stability of Euler Columns

Hammad JAMİL | Naki TÜTÜNCÜ

(2019)

About this article

Received

07 October 2016

Accepted

13 April 2017

Published

30 September 2017

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/jve.2017.17815

Keywords

functionally graded materials

moderately thick plate

free vibration

frequency

thermal environment

Acknowledgements

This research was supported by the National Natural Science Foundation of China (11262010, 11272278) and the Fundamental Research Funds for the Universities of Gansu (201405056001). The authors gratefully acknowledge both of the supports.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 01 08

Minimizing the radiated sound power from vibrating plates by using in-plane functionally graded materials

Nabeel Alshabatat, Koorosh Naghshineh

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2018 12 13

Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Jun Zhang, Tianyun Li, Xiang Zhu

Research article

2016 12 31

Vibration and post-buckling of a functionally graded beam subjected to non-conservative forces

Qing Lu Li, Jing Hua Zhang

Q.-L. Li, W.-D. Luan, and Z.-Q. Zhu, “Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments,” Journal of Vibroengineering, Vol. 19, No. 6, pp. 4423–4439, Sep. 2017, https://doi.org/10.21595/jve.2017.17815

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.17815
UR  - https://doi.org/10.21595/jve.2017.17815
TI  - Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments
T2  - Journal of Vibroengineering
AU  - Li, Qing-Lu
AU  - Luan, Wei-Di
AU  - Zhu, Zuo-Quan
PY  - 2017
DA  - 2017/09/30
PB  - JVE International Ltd.
SP  - 4423-4439
IS  - 6
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2017,
	doi = {10.21595/jve.2017.17815},
	url = {https://doi.org/10.21595/jve.2017.17815},
	year = 2017,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {6},
	pages = {4423--4439},
	author = {Qing-Lu Li and Wei-Di Luan and Zuo-Quan Zhu},
	title = {Shooting method for free vibration of {FGM} Reissner-Mindlin circular plates resting on elastic foundation in thermal environments},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Q.-L. Li, W.-D. Luan, and Z.-Q. Zhu, “Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments,” Journal of Vibroengineering, vol. 19, no. 6, pp. 4423–4439, Sep. 2017, doi: 10.21595/jve.2017.17815.

Copy IEEE

Copied to clipboard!

Li, Qing-Lu, Wei-Di Luan, and Zuo-Quan Zhu. “Shooting Method for Free Vibration of FGM Reissner-Mindlin Circular Plates Resting on Elastic Foundation in Thermal Environments.” Journal of Vibroengineering 19, no. 6 (September 30, 2017): 4423–39. https://doi.org/10.21595/jve.2017.17815.

Copy Chicago

Copied to clipboard!

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Abstract

1. Introduction

2. Problem formulation

2.1. Temperature field

2.2. Effective material properties of FGMs

2.3. Governing equations

2.4. Motion equations

2.5. Hamilton’s principle

3. Shooting method

4. Shooting method for approximate solutions of free vibration of FGM Reissner-Mindlin plates

4.1. Comparison studies

4.2. Numerical results and discussions

5. Conclusions

References

Cited by

About this article

Related Articles