Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Zhang, Jun; Li, Tianyun; Zhu, Xiang

doi:10.21595/vp.2018.20368

Vibroengineering Procedia

Browse Procedia

Published: 13 December 2018

Check for updates

Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Jun Zhang¹

Tianyun Li²

Xiang Zhu³

^{1, 2, 3}School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China

^{1, 2, 3}China Ship Development and Design Center, Wuhan, 430064, China

^{1, 2, 3}Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai, 200240, China

Corresponding Author:

Tianyun Li

Cite the article Download PDF

Downloads 1888

CrossRef Citations 1

Abstract

Rayleigh-Ritz method was introduced to analyze the vibration characteristics of functionally graded material (FGM) rectangular plate with complex boundary conditions. The Improved Fourier series was chosen as the admissible function for its great property to be used universally in various boundary conditions. The virtual spring model was adopted to simulate the complex boundary conditions. The strain and kinetic energy of the structure and elastic potential energy of the border were easily calculated by using relevant formula. Finally, comparing the result with the references, the accuracy and convergence can be proved.

1. Introduction

In recent years, a rapid development in science and technology nowadays motivated researchers to researching new kinds of materials. Being widely used in automotive, ocean engineering, aerospace, electronic, and nuclear industries because of its outstanding advantage such as good adaptability to temperature gradients or easy to get desired strength and stiffness, functionally graded materials (FGMs) are attracting more attention day by day.

A large number of methods have been used to deal with the vibration problems of FGM plates. For numerical method is better at problems of structures with complex geometry, various methods were proposed mainly based on the finite element method or meshless methods [1]. J. Yang [2]developed a one-dimensional differential quadrature approximation and the Galerkin procedure to analyse the free vibration, and the Modal Superposition Method was used to analyze the transient response of the plate structure. Relevant numerical methods have been well developed.

As for analytical methods, T. Y. Ng [3] analyse the effects of FGM materials plate structures on the parametric resonance of based on the assumed mode method and Hamilton’s principle. J. Woo [4]used an analytical solution to solve the problems of FGM plates for the nonlinear free vibration behaviour combining mixed Fourier series and von Karman theory. Sh. Hosseini-Hashemi [5]proposed an analytical solutions for vibration problems of FGM plates with elastic conditions. The analytical method was applied to the calculation of vibration problem of functionally gradient plates well, yet more research is needed as well.

In this paper, Rayleigh Ritz method was researched for solving the vibration problems of FGM plate. The improved Fourier series was chosen as the admissible function so that the traditional Rayleigh Ritz method can be used to calculate complex boundaries. Combining the first order shear deformation theory, the accuracy can be ensured. A numerical method was introduced to calculate the integration so that the efficiency of calculation is greatly improved. Numerical examples were given to prove the feasibility for solving the problem. Providing a reliable method for actual engineering problems.

2. Geometric models and properties of materials

Set an FGM rectangular plate as an example. The sale is length $a$ , width $b$ and total thickness $h$ . The plate is made from a mixture of two kinds of materials, and the composition is described as follows. The formulations are deduced here with the assumption of the linear elastic material behavior and small displacements and strains. The material properties varied with plate thickness can be expressed as:

1

X (z) = X_{m} V_{m} (z) + X_{c} V_{c} (z),

where $X$ denotes the effective material property such as density, Young’s modulus etc. $X_{m}$ and $X_{c}$ is the properties of the two different materials. $V_{m}$ and $V_{c}$ are the volume fraction of the material according to the conditions of:

2

V_{m} (z) + V_{c} (z) = 1,

3

V_{m} = {(\frac{2 z + h}{2 h})}^{k}, (k \geq 0) .

In which $k$ is the volume fraction exponent. Taking Eqs. (3) into the Eqs. (1), the following equation can be obtained:

4

X (z) = (X_{m} - X_{c}) {(\frac{2 z + h}{2 h})}^{k} + X_{c} .

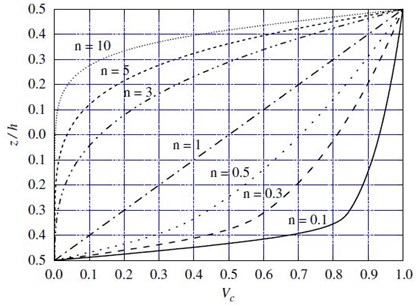
The relation between volume fraction and exponent is shown in Fig. 1 [6].

Fig. 1Variation of the volume fraction through the thickness

$Variation of the volume fraction through the thickness$

3. Theoretical formulations

In the study, the Rayleigh Ritz method was introduced to solve the problem. Before derived the characteristic equation, a suitable admissible functions shall be given through which the specific expression of strain energy, kinetic energy and elastic potential energy can be obtained.

Considering the first order shear theory, suppose admissible functions of the rectangular FGM plates can be expressed as:

5a

w (x, y) = \sum_{m = 1}^{M} \sum_{n = 1}^{N} A_{m n} φ_{m} (x) ψ_{n} (y) e^{i ω t},

5b

β_{x} (x, y) = \sum_{m = 1}^{M} \sum_{n = 1}^{N} B_{m n} φ_{m} (x) ψ_{n} (y) e^{i ω t},

5c

β_{y} (x, y) = \sum_{m = 1}^{M} \sum_{n = 1}^{N} C_{m n} φ_{m} (x) ψ_{n} (y) e^{i ω t} .

In which $w (x, y)$ is the flexural displacement, $β_{x} (x, y)$ is the rotation angle of the normal line along the $x z$ plane, and $β_{y} (x, y)$ is the rotation angle of the normal line along the $y z$ plane, $A_{m n}$ , $B_{m n}$ , $C_{m n}$ are unknown coefficients, $φ_{m} (x)$ , $ψ_{n} (y)$ are functions related to $x$ and $y$ respectively, $e^{i ω t}$ is harmonic time factor. The improved Fourier series is selected as the admissible function because it can satisfy arbitrary boundary conditions so that the virtual spring model can be introduced to simulate various complex boundary conditions, which can be expressed as [7]:

6a

\begin{array}{l} φ_{m} (x) = s i n (m π x) \begin{array}{l} , 0 < m < 5, \end{array} \\ φ_{m} (x) = c o s [(m - 5) π x], m \geq 5, \begin{array}{l}  \end{array} \end{array}

6b

\begin{array}{l} ψ_{n} (y) = s i n (n π x), \begin{array}{l} 0 < n < 5, \end{array} \\ ψ_{n} (y) = c o s [(n - 5) π x], n \geq 5, \begin{array}{l}  \end{array} \end{array}

where $m =$ 1, 2, 3, …, $M$ ; $n =$ 1, 2, 3, …, $N$ .

According to the first order shear theory, the strain energy can be expressed as:

7

V_{p} = \frac{1}{2} D (z) \int_{0}^{a} \int_{0}^{b} \{\begin{matrix} {(\frac{\partial β_{x}}{\partial x} + \frac{\partial β_{y}}{\partial y})}^{2} - 2 (1 - μ) \frac{\partial β_{x}}{\partial x} \frac{\partial β_{y}}{\partial y} + \frac{1}{2} (1 - μ) {(\frac{\partial β_{x}}{\partial y} + \frac{\partial β_{y}}{\partial x})}^{2} \end{matrix}\} d x d y + \frac{1}{2} k_{0} G h \int_{0}^{a} \int_{0}^{b} \{{(β_{x} + \frac{\partial w}{\partial x})}^{2} + {(β_{y} + \frac{\partial w}{\partial y})}^{2}\} d x d y .

In which $D (z) = E (z) h^{3} / 12 (1 - μ^{2})$ represent the bending stiffness, $E (z)$ is the Young’s modulus varies with the thick. $μ$ is the Poisson’s ratio, $k_{0} =$ 6/5 represent the shear coefficient, $G (z) = E (z) / 2 (1 + μ)$ is the shear stiffness, $h$ is the thickness.

The kinetic energy of plate can be given as:

8

T = \frac{1}{2} ρ (z) h ω^{2} \int_{0}^{a} \int_{0}^{b} \{w^{2} + \frac{1}{12} h^{2} ({β_{x}}^{2} + {β_{y}}^{2})\} d x d y,

where $ρ (z)$ is the mass density and $ω$ is the angular frequency.

The virtual spring model is used, and the effect of the boundary conditions on the vibration can be transformed into the influence of the elastic potential energy at the boundary to the stiffness matrix. Introducing displacement restrained springs and corner restrained springs with adjustable stiffness coefficient along the edges shown as Fig. 2.

Fig. 2Processing of boundary conditions

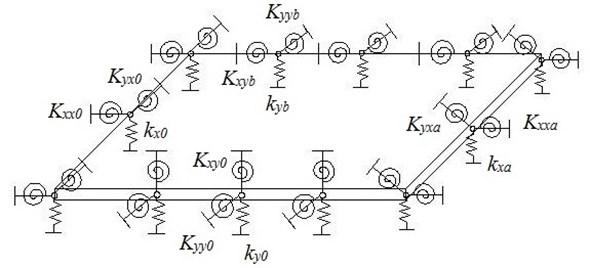
Supposing the displacement restrained springs constants and corner restrained springs constants are $k_{i j}$ (N/m²), $K_{y i j}$ (N/rad) and $K_{x i j}$ (N/rad) respectively. It is easy to simulate various complex boundary conditions by adjusting the stiffness of the two kinds of springs. The simulation of classical boundary conditions is shown in Table 1.

Table 1Classical boundary conditions corresponding spring values

	Clamped	Simply supported	Free
$k$ (N/m²)	∞	∞	0
$K$ (N/rad)	∞	0	0

Then the increased elastic energy at the boundary is:

9

\begin{array}{l} V_{s} = \frac{1}{2} {\int_{0}^{b} \{[k_{x 0} w^{2} + K_{x x 0} β_{x}^{2} + K_{y x 0} β_{y}^{2}]}_{x = 0} + {[k_{x a} w^{2} + K_{x x a} β_{x}^{2} + K_{y x a} β_{y}^{2}]}_{x = a}\} d y \\ + \frac{1}{2} {\int_{0}^{a} \{[k_{y 0} w^{2} + K_{x y 0} β_{x}^{2} + K_{y y 0} {β_{y}^{2}}^{2}]}_{y = 0} + {[k_{y b} w^{2} + K_{x y b} β_{x}^{2} + K_{y y b} β_{y}^{2}]}_{y = b}\} d x . \end{array}

The energy functional of the whole structure can be expressed as:

10

\prod = V_{p} + V_{s} - T .

Substituting Eqs. (7), (8), (9) into Eq. (10), and take the total energy for partial derivatives:

11

\frac{\partial \prod}{\partial A_{m n}} = 0, \frac{\partial \prod}{\partial B_{m n}} = 0, \frac{\partial \prod}{\partial C_{m n}} = 0 .

Then the vibration problem of the structure is transformed into the problem of solving eigenvalues, which can be expressed as follows:

12

(K - ω^{2} M) X = 0 .

In which, $K$ represent the stiffness matrix, $M$ represent the mass matrix of the structure, $X$ is the unknown coefficient vector.

4. Numerical analysis

When calculating, it takes a long time to calculate the integral. In order to improve the efficiency, numerical method is introduced. By dividing the plate structure into several small units, the calculation of integral is converted into calculating the summation.

Example 1. The values of truncated number $M$ , $N$ in the admissible function have a great influence on the accuracy of the calculation. Square plate with free boundary condition (FFFF) was chosen as examples. The parameters of the model are as follows: the length is $a =$ 1 m, and the thickness is $h =$ 0.1 m. Table 2 compares the frequencies (for $h$ / $a =$ 0.1) calculated by using different number of terms in the series. When $M = N =$ 12, the natural frequency tends to be a constant, which can be considered the method has converged.

Example 2. The length of the plate is $a =$ 1 m. When $k =$ 0, 0.5, 1, 4, 10, natural frequencies of the square FGM plates with different thickness to length ratios ( $h$ / $a =$ 0.05, and 0.2) are given in Table 3. The boundary condition are SSSS. The plates are made of aluminum (Al, $E =$ 70 GPa, $ρ =$ 2702 kg/m³, $μ =$ 0.3) and alumina (Al₂O₃, $E =$ 380 GPa, $ρ =$ 3800 kg/m³, $μ =$ 0.3). By comparing the results with the references, the accuracy of the method can be proved.

Example 3. Changing the materials, Table 4. shows the results of the square plates with the length ratios of $h$ / $a =$ 0.1 for the Al/ZrO₂(ZrO₂, $E =$ 200 GPa, $ρ =$ 5700 kg/m³, $μ =$ 0.3). Only the results for the first four modes are given. At the boundary conditions of SSSS and CFFF, comparing with the reference, the present method is accurate for solving the problems of FGM plates.

Table 2Nature frequencies of rectangular plates (γ=ωa2/hρm/Em, Al/Al2O3, (h/a= 0.1))

Mode	$M = N =$ 9	$M = N =$ 10	$M = N =$ 11	$M = N =$ 12	$M = N =$ 13	$M = N =$ 14
1	2.96	2.95	2.95	2.94	2.94	2.94
2	4.39	4.39	4.39	4.39	4.39	4.39
3	5.41	5.41	5.41	5.41	5.41	5.41
4	7.44	7.43	7.42	7.41	7.41	7.40

Table 3Comparison of natural frequencies of FGM plate (γ=ωhρm/Em, SSSS, Al/Al2O3)

$δ = h / a$	Reference	Gradient index
$δ = h / a$	Reference	0	0.5	1	4	10
0.05	Pre.	0.01446	0.01228	0.01107	0.00960	0.00919
	Ref. [5]	0.01480	0.01281	0.01150	0.01013	0.00963
	Ref. [6]	0.01464	0.01241	0.01118	0.00970	0.00931
0.2	Pre.	0.19861	0.16994	0.15367	0.13136	0.12430
	Ref. [5]	0.21120	0.18060	0.16500	0.13710	0.13040
	Ref. [6]	0.20550	0.17570	0.15870	0.13560	0.12840

Table 4Natural frequencies of FGM plate (γ=ωa2/hρm/Em, Al/ZrO2, h/a= 0.1)

		SSSS				CFFF
Mode	–	1	2	3	4	1	2	3	4
0	Pre.	5.545	13.471	13.471	20.453	1.038	2.439	6.09	7.734
–	Ref. [6]	5.676	13.537	13.537	20.633	1.03	2.391	6.005	7.636
0.5	Pre.	4.997	12.149	12.149	18.465	0.934	2.197	5.486	6.965
–	Ref. [6]	5.111	12.207	12.207	18.63	0.926	2.153	5.409	6.051
1	Pre.	4.764	11.58	11.58	17.595	0.891	2.095	5.229	6.639
–	Ref. [6]	4.871	11.633	11.633	17.748	0.883	2.052	5.155	5.76
2	Pre.	4.592	11.152	11.152	16.923	0.86	2.02	5.042	6.402
–	Ref. [6]	4.698	11.199	11.199	17.063	0.853	1.979	4.968	5.444

5. Conclusions

The Rayleigh-Ritz method was introduced to analyze the free vibration characteristic. Combined with the first order shear theory, the accuracy can be ensured. Besides, virtual spring model was adopted to simulate the complex boundary conditions. Several examples were given, comparing the frequencies with the references, good convergence and accuracy can be proved. There is a unique advantage that the programming of the method is simple comparing with FEM when the parameter of the calculation model changed. What is important is that: the present method can be easily combined with other method when analyzing more complicated problems.

References

Swaminathan K., Naveenkumar D. T., Zenkour A. M., Carrera E. Stress, vibration and buckling analyses of FGM plates – a state-of-the-art review. Composite Structures, Vol. 120, 2015, p. 10-31.

Publisher
Yang J., Shen Hui Shen Dynamic response of initially stressed functionally graded rectangular thin plates. Composite Structures, Vol. 54, Issue 4, 2001, p. 497-508.

Publisher
Ng T. Y., Lam K. Y., Liew K. M. Effects of FGM materials on the parametric resonance of plate structures. Computer Methods in Applied Mechanics and Engineering, Vol. 190, Issues 8-10, 2000, p. 953-962.

Publisher
Woo J., Meguid S. A., Ong L. S. Nonlinear free vibration behavior of functionally graded plates. Journal of Sound and Vibration, Vol. 289, Issue 3, 2006, p. 595-611.

Publisher
Sh Hosseini Hashemi, Rokni Damavandi Taher H., Akhavan H., Omidi M. Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Applied Mathematical Modelling, Vol. 34, Issue 5, 2010, p. 1276-1291.

Publisher
Zhao X., Lee Y. Y., Liew K. M. Free vibration analysis of functionally graded plates using the element-free KP-Ritz method. Journal of Sound and Vibration, Vol. 319, Issue 3, 2009, p. 918-939.

Publisher
Li W. L. Vibration analysis of rectangular plates with general elastic boundary supports. Journal of Sound and Vibration, Vol. 273, Issue 3, 2004, p. 619-635.

Publisher

Cited by

Advances in Mechanical Design

Yuhang Zhang | Wenguang Liu | Chao Liu | Zhipeng Lyu

(2022)

About this article

Received

12 November 2018

Accepted

26 November 2018

Published

13 December 2018

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2018.20368

Keywords

FGM plate

Rayleigh-Ritz method

energy method

complex boundary conditions

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2019 11 28

Free vibration of circular annular plate with different boundary conditions

Yash Jaiman, Baij Singh

Research article

2019 04 25

Vibration of thin elastic FGM plates with multi-gradation effects

Ladislav Sator, Vladimir Sladek, Jan Sladek

Research article

2016 08 15

A unified solution for free vibration of orthotropic circular, annular and sector plates with general boundary conditions

Dongyan Shi, Qian Liang, Qingshan Wang, Xiaoyan Teng

J. Zhang, T. Li, and X. Zhu, “Free vibration analysis of FGM plates based on Rayleigh-Ritz method,” Vibroengineering PROCEDIA, Vol. 21, pp. 53–58, Dec. 2018, https://doi.org/10.21595/vp.2018.20368

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20368
UR  - https://doi.org/10.21595/vp.2018.20368
TI  - Free vibration analysis of FGM plates based on Rayleigh-Ritz method
T2  - Vibroengineering PROCEDIA
AU  - Li, Tianyun
AU  - Zhang, Jun
AU  - Zhu, Xiang
PY  - 2018
DA  - 2018/12/13
PB  - JVE International Ltd.
SP  - 53-58
VL  - 21
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2018,
	doi = {10.21595/vp.2018.20368},
	url = {https://doi.org/10.21595/vp.2018.20368},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	pages = {53--58},
	author = {Tianyun Li and Jun Zhang and Xiang Zhu},
	title = {Free vibration analysis of {FGM} plates based on Rayleigh-Ritz method},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]T. Li, J. Zhang, and X. Zhu, “Free vibration analysis of FGM plates based on Rayleigh-Ritz method,” Vibroengineering PROCEDIA, vol. 21, pp. 53–58, Dec. 2018, doi: 10.21595/vp.2018.20368.

Copy IEEE

Copied to clipboard!

Li, Tianyun, Jun Zhang, and Xiang Zhu. “Free Vibration Analysis of FGM Plates Based on Rayleigh-Ritz Method.” Vibroengineering PROCEDIA 21 (December 13, 2018): 53–58. https://doi.org/10.21595/vp.2018.20368.

Copy Chicago

Copied to clipboard!

Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Abstract

1. Introduction

2. Geometric models and properties of materials

3. Theoretical formulations

4. Numerical analysis

5. Conclusions

References

Cited by

About this article

Related Articles